Einzelpfahlbemessung nach ACI 318 (2014)
Pfähle sind lange und schlanke Elemente, die die Lasten vom Oberbau auf tieferen Boden oder auf einen Fels mit ausreichender Tragfähigkeit übertragen. Materialien, die für Pfähle verwendet werden, können Holz sein, Stahl, und Beton. Das Einbringen des Pfahls in den Boden kann gerammt werden, gebohrt, oder aufgebockt, die dann mit Pfahlkappen verbunden werden. Viele Faktoren, wie Standortbedingungen, Bodenart, die Übertragung von Lasten, werden als Klassifizierung der Art und Installation von Pfählen angesehen. Dieser Artikel konzentriert sich auf die Auslegung eines Betonpfahls in Übereinstimmung mit dem American Concrete Institute (ACI) 318 – 2014.
Das SkyCiv Foundation Design-Modul umfasst die Bemessung von Pfählen gemäß dem American Concrete Institute (ACI 318) und australische Standards (AS 2159 & 3600).
Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Unser kostenloses Tool ermöglicht es Benutzern, Tragfähigkeitsberechnungen durchzuführen, ohne dass ein Download oder eine Installation erforderlich ist!
Tragfähigkeit eines Stapels
Allgemein, Vertikallasten auf Pfähle werden vom Endlager des Pfahls aufgenommen, und der entlang seiner Länge entwickelte Hautreibungswiderstand. Die ultimative Tragfähigkeit (Q.U.) soll durch Gleichung dargestellt werden (1). Die zulässige Tragfähigkeit wird mit einem Sicherheitsfaktor berechnet (Q.Ein).
\({Q.}_{u} = {Q.}_{p} + {Q.}_{s}\) (1)
Q.U. = maximale Tragfähigkeit
Q.P. = Endlagerwiderstand
Q.S. = Hautreibungswiderstand
\({Q.}_{Ein} = frac{{Q.}_{U.}}{FOS} \) (2)
Q.Ein = Zulässige Tragfähigkeit
FOS = Sicherheitsfaktor
Für eine ausführlichere Anleitung, Lesen Sie unseren Artikel zum Rechnen der Hautreibungswiderstand und die Endtragfähigkeit.
Strukturfestigkeit eines einzelnen Pfahls
Pfähle werden auch axialen Kräften ausgesetzt, Querkraft, und Biegemoment, deshalb sind sie säulenähnlich aufgebaut. Sektion 10.5.1.1 besagt, dass alle faktorisierten Lasten ihre entsprechenden Bemessungsfestigkeiten nicht überschreiten dürfen.
\( {øP}_{N.} ≤ {P.}_{U.} \) (3ein)
\( {wund}_{N.} ≤ {M.}_{U.} \) (3b)
\( {øV}_{N.} ≤ {V }_{U.} \) (3c)
P.U., M.U., V U. = Faktorisierte axiale, Biegemoment, Querlasten
P.N., M.N., V N. = Nenn axial, Biegemoment, Querlasten
ø = Festigkeitsminderungsfaktoren (Tabelle 1)
| Faktoren zur Reduzierung der Festigkeit(φ) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Axial | 0.65-0.90 | ||||||||||||
| Biege | 0.65-0.90 | ||||||||||||
| Scheren | 0.75 | ||||||||||||
Tabelle 1: Faktoren zur Reduzierung der Festigkeit (Tabelle 21.2.1, ACI 318-14)
Scherkapazität eines einzelnen Pfahls (øVN.)
Die nominelle Schubfestigkeit muss den kombinierten Beiträgen der Schubtragfähigkeiten von Beton und Stahlbewehrung entsprechen.
Scherfestigkeit von Beton (V c)
Der Beitrag des Betons zur Schubtragfähigkeit wird wie in Gleichung gezeigt berechnet (4) die auf Abschnitt . definiert ist 22.5.5.1 von ACI 318-14.
\( {V }_{c} = 0.17 × λ × sqrt{fc’} × b × d \) (4)
λ = Betonmodifikationsfaktor = 1 (Normalbeton, Tabelle 19.2.4.2)
fc’ = Festigkeit des Betons
b = Pfahlbreite oder -durchmesser
d = 0.80 × Pfahltiefe (Sektion 22.5.2.2)
Scherfestigkeit von Stabstahl (V s)
Der Beitrag der Querschubbewehrung zur Querkrafttragfähigkeit wird als Minimum zwischen den Gleichungen berechnet (5) und (6).
\( {V }_{s} = 0.066 × sqrt{fc’} × b × d \) (5)
\( {V }_{s} = frac{{Ein}_{v} × {f}_{yt} × d }{s} \) (6)
EinV = Fläche der Schubbewehrungsstäbe
fyt = Streckgrenze der Schubbewehrungsstäbe
s = Mittenabstand der Schubbewehrungsstäbe
Nominale Scherfestigkeit (øVN.)
Zusammenfassen der Ausgabe von Gleichung 4-6 ergibt sich die Nennscherfestigkeit des Pfahls. Festigkeitsreduktionsfaktor (Ö) soll gleich sein 0.75 wie in Tabelle definiert 22.2.1 von ACI 318-14.
\( {øV}_{N.} = ø × ({V }_{c} + {V }_{s}) ≤ {øV}_{U.} \) (7)
Axial- und Biegetragfähigkeit eines einzelnen Pfahls (øPN., wundN. )
Axial- und Biegetragfähigkeiten werden anhand eines Interaktionsdiagramms überprüft. Dieses Diagramm ist eine visuelle Darstellung des Verhaltens der Biege- und Axialkapazitäten durch eine Belastungserhöhung vom reinen Biegepunkt bis zum Erreichen eines ausgeglichenen Punktes.
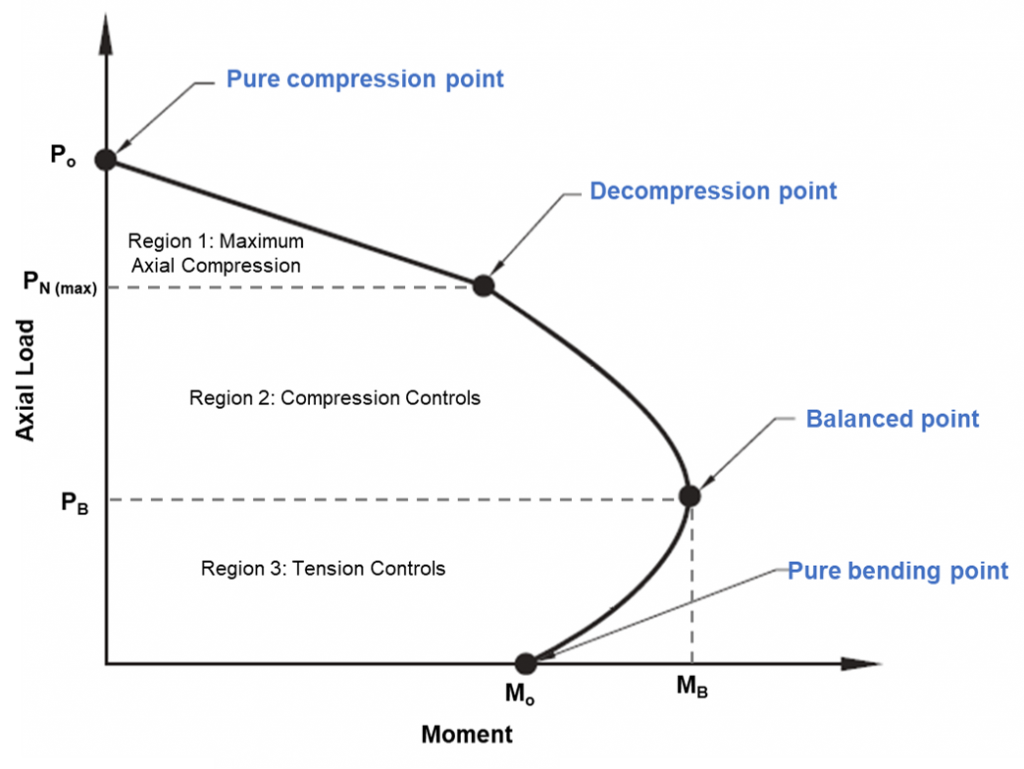
Abbildung 1: Säuleninteraktionsdiagramm
Säuleninteraktionsdiagramm
Der reine Kompressionspunkt im Diagramm ist der Punkt, an dem der Pfahl die Kompression versagt. An dieser Stelle, Die Axiallast wird auf den plastischen Schwerpunkt des Profils aufgebracht, um ohne Biegung unter Druck zu bleiben. Die Festigkeit des Pfahls zwischen dem reinen Druckpunkt bis zum Dekompressionspunkt kann durch lineare Interpolation berechnet werden. Der Dekompressionspunkt ist dort, wo die Betondehnung an der extremen Druckfaser gleich 0.003, und die Dehnung in der extrem zugfesten Faser ist null. Der reine Biegepunkt ist dort, wo die axiale Tragfähigkeit Null ist. Zwischen dem Übergang vom Dekompressionspunkt zum reinen Biegepunkt, ein ausgeglichener Zustand wird erreicht. An dieser Stelle, die Betondehnung ist am Limit (ec=0,003), und die äußere Stahldehnung erreicht Streckgrenze (es=0,0025). Jede Kombination von Axiallast und Biegemoment außerhalb des Diagramms führt zum Ausfall.
Maximale nominelle axiale Druckfestigkeit für die Auslegung (øPN.)
Die Bemessungsaxialfestigkeit eines Abschnitts darf nur begrenzt werden auf 80-85% der nominellen Axialfestigkeit zur Berücksichtigung der zufälligen Exzentrizität.
\( {øP}_{N.} = ø × {P.}_{Das} \) (8ein)
\( {P.}_{Das} = F × [0.85 × {f}_{c} × ({Ein}_{G} – {Ein}_{st}) + ({f}_{j} × {Ein}_{st}) ] \) (8b)
F = 0.80 (Krawatten)
F = 0.85 (Spiral)
EinG = Bruttofläche des Pfahlquerschnitts
Einst = Gesamtfläche der Längsstahlstäbe
fj = Streckgrenze von Stabstahl
Nominale Biegefestigkeit (wundN.)
Die Konstruktion des Interaktionsdiagramms für die Säule umfasst das Auftragen einer Reihe von Werten von PN. und MN.. Werte für PN. muss der Summe der Zug- und Druckkräfte entsprechen, wie in den Abbildungen 2a und 2b gezeigt, während das entsprechende MN. berechnet sich durch Auflösen dieser Kräfte um die neutrale Achse. Diese Kräfte umfassen die Druckkraft, die auf die Druckfläche wirkt, und die Kräfte, die von jedem der Bewehrungsstäbe ausgeübt werden, die entweder Druck- oder Zugkräfte sein können. Im Folgenden wird ein allgemeines Verfahren vorgeschlagen, um ein Interaktionsdiagramm unter Verwendung der vorgestellten Gleichungen zu erstellen.
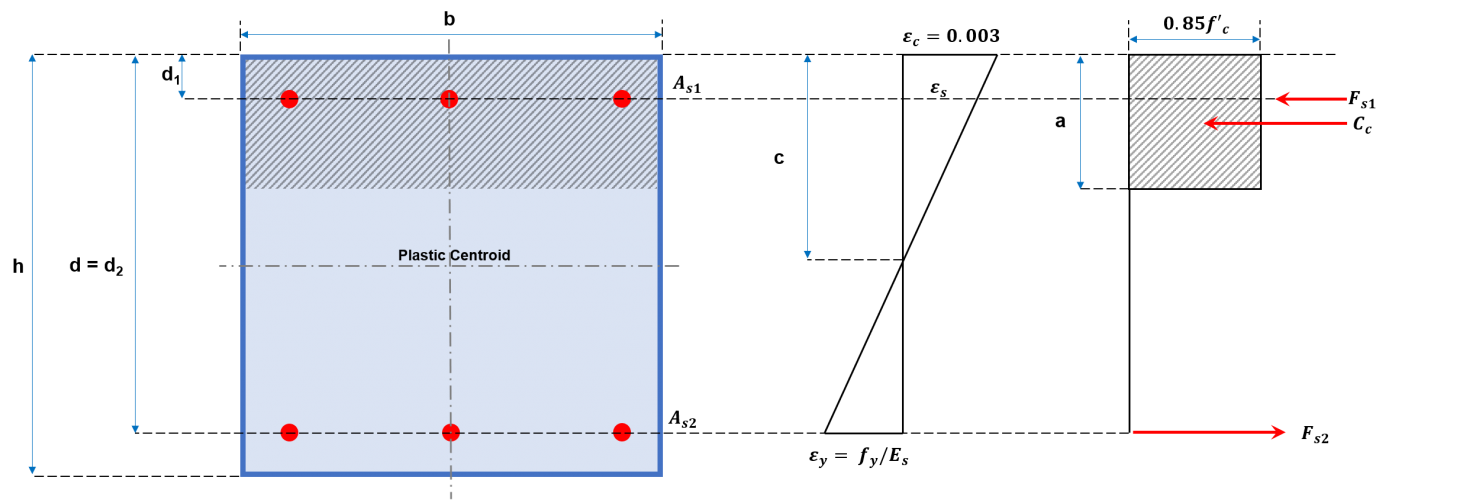
Abbildung 2a: Rechteckiger Säulenquerschnitt
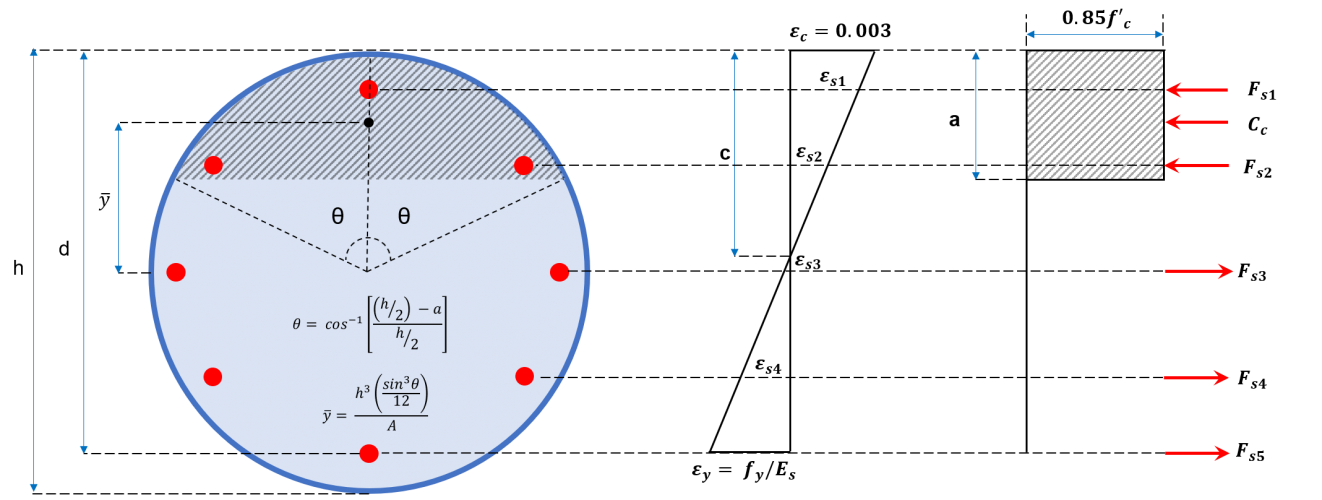
Abbildung 2b: Runder Säulenquerschnitt
Allgemeine Vorgehensweise für das Interaktionsdiagramm einer Säule
(1) Berechnen Sie den Wert von PDas und PN. (Gleichungen 8a und 8b).
(2) Bestimmen Sie c und die Dehnungen in den Bewehrungen.
\( c = 0.003 × frac{{d}_{1}}{0.003 + (MIT + {e}_{j})} \) (9)
c = Tiefe der neutralen Achse
ej = Stahldehnung = fj/E.s
Z = Beliebiger Wert (0, -0.5, -1.0, -2.5)
Eine Reihe von Fällen ist zu berücksichtigen, indem verschiedene Positionen der neutralen Achse ausgewählt werden, c. So legen Sie die Positionen der neutralen Achse fest, verschiedene Stahldehnungen sind durch Multiplikation eines beliebigen Wertes Z mit der Streckgrenze des Stahls auszuwählen. Es gibt einen großen Wertebereich für Z. Jedoch, es gibt nur vier obligatorische Punkte für das Interaktionsdiagramm.
- Z = 0: an dieser Stelle, die Dehnung an der äußersten Zugschicht ist null. Dieser Punkt markiert den Wechsel von einer auf allen Längsstäben zulässigen Drucküberlappungsverbindung zu einer Zugüberlappungsverbindung.
- Z = -0.5: diese Dehnungsverteilung beeinflusst die Länge der Zugüberlappungsverbindung in einer Stütze & wird üblicherweise in einem Interaktionsdiagramm aufgetragen.
- Z = -1: dies markiert den Punkt eines ausgeglichenen Zustands. Diese Dehnungsverteilung kennzeichnet den Übergang von Druckversagen, die durch Quetschen der Druckfläche des Querschnitts entstehen, zu Zugversagen, die durch die Streckung der Längsbewehrung ausgelöst werden.
- Z = -2.5: dieser Punkt entspricht der zugkontrollierten Dehnungsgrenze von 0.005.
(3) Berechnung der Spannungen in den Bewehrungslagen.
\({f}_{und} ={e}_{und} × {E.}_{s} \) (10)
fund = Spannung in Stahl
eund = Dehnung in Stahl
\({e}_{und} = frac{c -{d}_{ich}}{c} × 0.003 \) (11)
E.s = Elastizitätsmodul von Stahl
(4) Bestimmen Sie die Höhe des Druckspannungsblocks, ein.
\(a = {b}_{1} × c \) (ein ≤ h)(12)
Für f’c ≤ 4000 psi (28 MPa):
b1 = 0.85
Für f'c > 4000 psi (28 MPa):
\( {b}_{1} = 0.85 – \frac{0.05 × (f’c – 4000)}{1000} \) (Kaiserliche)
\( {b}_{1} = 0.85 – \frac{0.05 ×(f’c – 28)}{7} \) (Metrisch)
(5) Berechnen Sie die Kräfte in Beton und Stahl.
Fläche des Druckspannungsblocks:
\({Ein}_{c} = a × b \) (Rechteckiger Querschnitt)
\({Ein}_{c} ={h}^{2} × frac{θ – sinθ cos}{4} \) (Kreisförmiger Querschnitt)
Druckkraft in Beton:
\({C.}_{c} = (0.85 × f’c) × {Ein}_{c}\) (14)
Zugkraft in Stahl (dich≤ a):
\({F.}_{und} = {f}_{und} × {Ein}_{und} \) (15)
Druckkraft in Stahl (dich > ein):
\({F.}_{und} = [{f}_{und} – (0.85 × f’c)] × {Ein}_{und} \) (16)
(6) Berechnen Sie die axiale Tragfähigkeit (P.N.).
\({P.}_{N.} = {C.}_{c} + Σ {F.}_{und} \) (17)
(7) Berechnen Sie die Biegetragfähigkeit (M.N.).
\({M.}_{N.} = [{C.}_{c} × (\frac{h}{2} – \frac{ein}{2})]+ Σ [{F.}_{und} × (\frac{h}{2} – {d}_{ich}) \) (18)
(8) Berechnen Sie den Wert des Festigkeitsminderungsfaktors (Ö).
Wie in Tabelle gezeigt 1, der Festigkeitsreduktionsfaktor sowohl für die axiale als auch für die Biegung variiert von 0.60 zu 0.90. Sektion 21.2 von ACI 318-14 zeigt seinen Wert für den Moment, Axialkraft, oder kombinierte Moment- und Axialkraft, wie in Tabelle gezeigt 2 unten.
| Einstufung | Spiral | Gebunden |
|---|---|---|
| Kompression kontrolliert | 0.75 | 0.65 |
| Übergang von Druck auf Zug | 0.75 + [50 × (et – 0.003) ] | 0.65 + [(250/3) × (et – 0.003) ] |
| Spannungsgesteuert | 0.90 | 0.90 |
Tabelle 2: Festigkeitsminderungsfaktoren für Axial, Moment oder kombiniere axial und moment (Tabelle 21.2.2, ACI 318-14)
(9) Schritte wiederholen 2-8 mit verschiedenen Werten für Z.
(10) Tragen Sie die Werte von øP . in das Diagramm einN. und øMN..
Betonpfahldesign mit SkyCiv Free Foundation Calculator
SkyCiv Free Foundation-Rechner hilft Ihnen bei der Konstruktion von Betonpfählen und anderen Aufgaben wie der Konstruktion von Fundamenten und Betonpfählen. Probieren Sie es jetzt aus, um herauszufinden, wie unser Rechner Ihnen bei Ihrem Betonpfahlprojekt helfen kann!
Verweise
-
- Bauvorschriften für Konstruktionsbeton (2014). AC! 318-14 Amerikanisches Betoninstitut.
- Hsiao, J.K. (2012). Auswirkungen der Biegeachse auf das Lastmoment (P-M) Interaktionsdiagramme für runde Betonstützen mit einer begrenzten Anzahl von Längsbewehrungsstäben. Elektronische Zeitschrift für Bautechnik 12 (1). Von http . abgerufen://www.ejse.org


