Das Fundament ist ein wesentliches Element einer Struktur, um die Gesamtstabilität zu gewährleisten, indem die Gesamtlasten der Struktur auf den Boden übertragen und verteilt werden. Flache Fundamente, wie rechteckige oder quadratische isolierte Fundamente, sind aufgrund der Einfachheit ihrer Konstruktion und der Gesamtkosten im Vergleich zu Tieffundamenten die bevorzugte Art von Fundamenten. Die Schätzung des Basisdrucks hat erhebliche Auswirkungen auf die Gestaltung und Größe des Fundaments. Normalerweise, Das Nutzverhältnis zwischen der zulässigen Tragfähigkeit des Bodens und dem maßgebenden Grunddruck unter dem Fundament ist die Grundlage für die Ausgangsgröße des Fundaments. Sobald die anfänglichen Fundamentabmessungen festgelegt sind, weitere Konstruktionsprüfungen für Sicherheit und Stabilität, wie Einweg- und Zweiwegschere, Biegefähigkeit, und Entwicklungslängenprüfungen, werden je nach verwendetem Designcode überprüft.

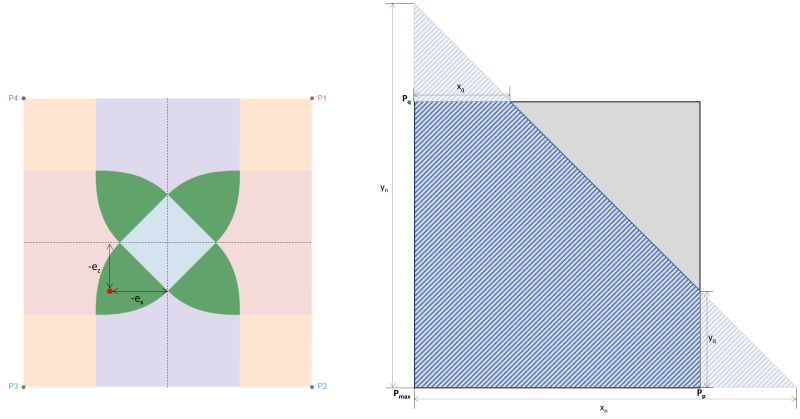
Wenn ein Fundament einer biaxialen Biegung ausgesetzt wird (M._x, M._mit), Es wird davon ausgegangen, dass die axiale Belastung (P.) wirkt auf eine Exzentrizitätskoordinate (e_x, e_mit) wo eine Tendenz besteht, sich vom Zentrum aus zu drehen. Die Wechselwirkung zwischen Boden und Fundament hängt hauptsächlich von der Dimension des Fundaments und der daraus resultierenden Exzentrizität der aufgebrachten Lasten ab. Je nach Lage der resultierenden Exzentrizität, Der Basisdruck bewirkt, dass das Fundament vollständig oder teilweise komprimiert wird. In der Praxis, Es wird empfohlen, ein Fundament mit voller Kompression zu entwerfen. Teilweise Kompression oder Verlust des Kontakts zwischen Boden und Fundament sollten nicht vernachlässigt werden, Die meisten Designer vermeiden dieses Szenario jedoch aufgrund der Komplexität der Berechnung. Das Fundament ist vollständig komprimiert, wenn sich die resultierende Exzentrizität innerhalb des Kerns oder unter Zone C befindet. Exzentrizität außerhalb von Zone C versetzt das Fundament in teilweise Kompression. Abbildung 1 zeigt die verschiedenen ausgewiesenen Zonen auf einer rechteckigen Basis.

Dieser Artikel konzentriert sich auf die Berechnung des Eckdrucks unter verschiedenen Zonenklassifizierungen basierend auf Bellos & Verfolgen (2017) und S.S. Rays (1995) Studien.

Zonenklassifikationen eines rechteckigen Fundaments

Die Zonenklassifizierungen eines rechteckigen Fundaments werden aus mehreren Studien verschiedener Autoren abgeleitet, um einen praktischen Ansatz zur Schätzung der Verteilung des Bodendrucks unter erwarteten Belastungsbedingungen zu entwickeln. Wie in Abbildung gezeigt 1, Es gibt fünf verschiedene Regionen (Zonen A-E) abhängig vom Ort der resultierenden Exzentrizität. Jede Zone entspricht einer anderen Belastung, Grunddruckverteilung, und Verformung. Zone C., auch Kern genannt, ist der Hauptkern. Es ist die ideale Region, um eine Grundlage zu schaffen, Dies führt zu einer vollständigen Kompression des Fundaments. Die Abmessungen dieser Region sind äquivalent zu 1/6 seiner jeweiligen Fundamentlänge.

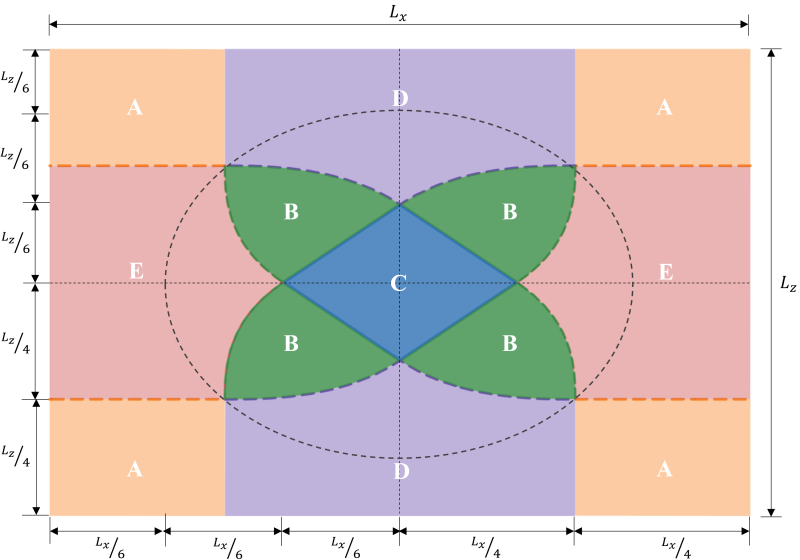
Abbildung 1: Zonenklassifikationen eines rechteckigen Fundaments

 

Der sekundäre Kern ist der elliptische Bereich (in Figur durch die gestrichelte Linie begrenzt 1) wobei seine großen und kleinen Halbachsen gleich sind 1/3 seiner jeweiligen Fundamentlänge. Diese Region umfasst die gesamten Zonen B & C und einige Teile der Zonen D & E.. Der sekundäre Kern führt zu einer teilweisen Komprimierung des Fundaments. Es empfiehlt sich, die Exzentrizität innerhalb der sekundären Zone für eine akzeptable Fundamentkonstruktion beizubehalten.

Die Exzentrizität über die sekundäre Zone hinaus ist das Ergebnis einer hohen biaxialen Belastung. Es umfasst die gesamte Zone A und die restlichen Teile der Zone D & E.. Es wird empfohlen, die Fundamente in diesen Bereichen nicht zu entwerfen, da die Gefahr des Umkippens besteht. Daher, Es empfiehlt sich, die Fundamentmaße für diese Belastungsart neu zu gestalten.

 

Im Folgenden sind die analytischen Formeln zum Lösen der Eckendrücke in jeder Zonenklassifikation aufgeführt.

Zone C. (Hauptkern, Vollständige Kompressionszone)

Wie erwähnt, Dies ist der am meisten bevorzugte Fall für die Gestaltung von Fundamenten, da dadurch die gesamte Basis des Fundaments unter Druck gesetzt werden kann, wie in Abbildung gezeigt 2. Dieser Fall wird durch eine geringe oder keine Exzentrizität innerhalb des Kerns dargestellt. Abbildung 2 zeigt die Exzentrizität innerhalb des Kerns mit seinem maximalen Druck an den Ecken P3 & P4 und Mindestdruck an den Ecken P1 & Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind.

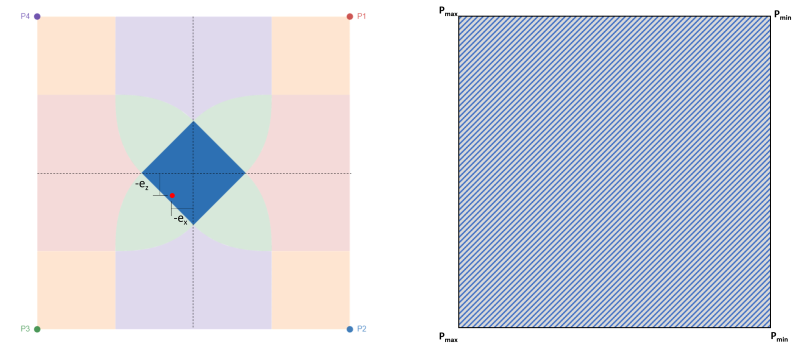
Abbildung 2: Exzentrizität (-e_x, -e_mit) in Zone C & voller Kompressionsbereich

Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung & minimale Eckdrücke (Schön & Verfolgen, 2017):

 

 

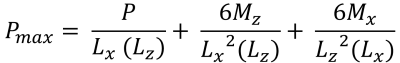
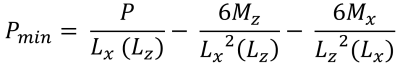
Eckdrücke basierend auf Exzentrizität
	P.1	P.2	P.3	P.4
+ex, +emit	P.max	P.max	P.Mindest	P.Mindest
+ex, -emit	P.max	P.max	P.Mindest	P.Mindest
-ex, -emit	P.Mindest	P.Mindest	P.max	P.max
-ex, +emit	P.Mindest	P.Mindest	P.max	P.max

Zone A. (Dreieckige Kompressionszone)

Dieser Fall entspricht vier rechteckigen Bereichen in jeder Ecke des Fundaments. Es tritt normalerweise mit großer biaxialer Exzentrizität auf, Dadurch wird in einer der Ecken eine hohe dreieckige Druckfläche erzeugt, wie durch den schattierten Bereich in der Abbildung dargestellt 3. Die verbleibenden Ecken verlieren den Kontakt zum Boden. Daher, Dieser Fall ist für das Design nicht empfehlenswert.

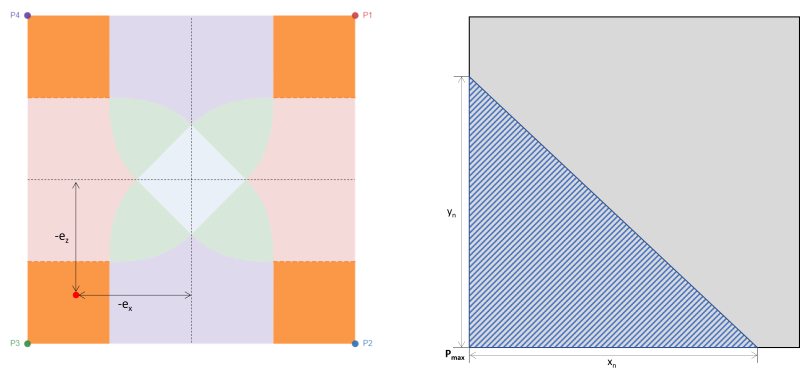Abbildung 3: Exzentrizität (-e_x, -e_mit) in Zone A & dreieckiger Kompressionsbereich um P3

 

Maximaler Druck (Schön & Verfolgen, 2017):

 

 

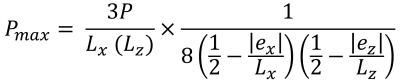
Eckdrücke basierend auf Exzentrizität
	P.1	P.2	P.3	P.4
ex(+), emit(+)	P.max	0	0	0
ex(+), emit(-)	0	P.max	0	0
ex(-), emit(-)	0	0	P.max	0
ex(-), emit(+)	0	0	0	P.max

Zone D. (Trapezförmige Kompressionszone)

Zone D entspricht auch großen Exzentrizitäten in den Bereichen, die in x-Richtung des Fundaments angebracht sind, wie in Abbildung gezeigt 4. Die Exzentrizität in Z-Richtung (e_mit) ist viel größer als in x-Richtung (e_x). In diesem Fall, Zwei Ecken des Fundaments verlieren den Kontakt zum Boden und erzeugen eine trapezförmige Druckfläche. Im Vergleich zu Zone A, die vollständig außerhalb der Sekundärzone liegt, ein Teil der Zone D ist noch von der Sekundärzone bedeckt.

 

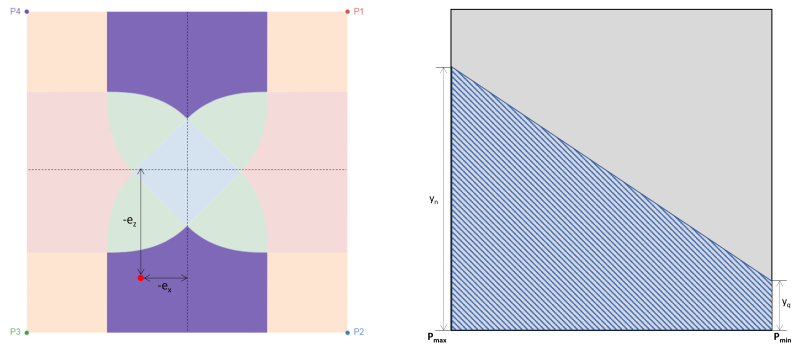
Abbildung 4: Exzentrizität (-e_x, -e_mit) in Zone D & trapezförmiger Kompressionsbereich um P3

 

Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung & minimale Eckdrücke (Schön & Verfolgen, 2017):

 

 

 

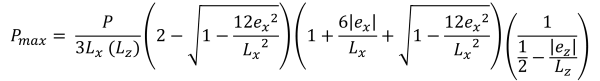
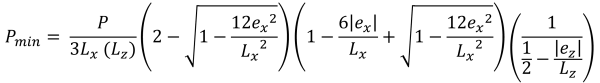
Vertikale Höhen der trapezförmigen Druckfläche (Schön & Verfolgen, 2017):

 

 

 

 

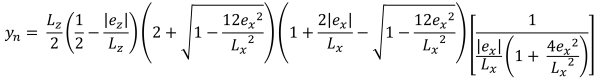
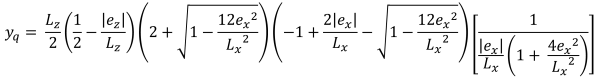
Eckdrücke basierend auf Exzentrizität
	P.1	P.2	P.3	P.4
ex(+), emit(+)	P.max	0	0	P.Mindest
ex(+), emit(-)	0	P.max	P.Mindest	0
ex(-), emit(-)	0	P.Mindest	P.max	0
ex(-), emit(+)	P.Mindest	0	0	P.max

 

Zone E. (Trapezförmige Kompressionszone)

Ähnlich wie Zone D, Auch in diesem Fall entsteht eine trapezförmige Druckfläche, die jedoch durch eine große Exzentrizität in x-Richtung verursacht wird(e_x).

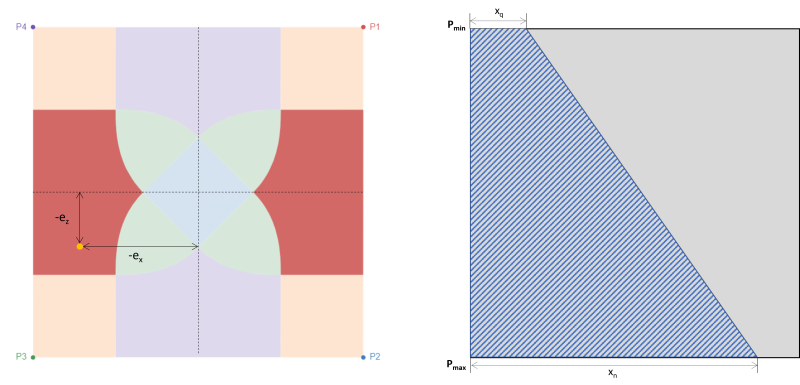Abbildung 5: Exzentrizität (-e_x, -e_mit) in Zone E & trapezförmiger Kompressionsbereich um P3

 

Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung & minimale Eckdrücke (Schön & Verfolgen, 2017):

 

 

 

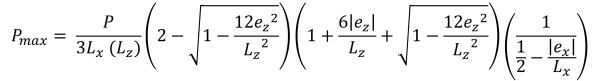
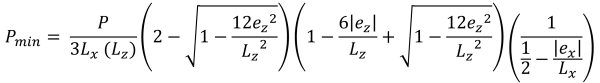
Horizontale Grundflächen der trapezförmigen Druckfläche (Schön & Verfolgen, 2017):

 

 

 

 

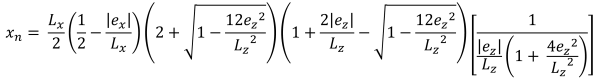
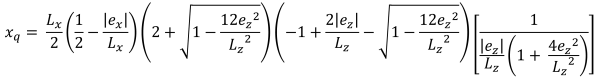
Eckdrücke basierend auf Exzentrizität
	P.1	P.2	P.3	P.4
ex(+), emit(+)	P.max	P.Mindest	0	0
ex(+), emit(-)	P.Mindest	P.max	0	0
ex(-), emit(-)	0	0	P.max	P.Mindest
ex(-), emit(+)	0	0	P.Mindest	P.max

Zone B. (Fünfeckige Kompressionszone)

Dieser Fall tritt auf, wenn die auf die Fundamente ausgeübten Lasten eine mäßige Exzentrizität innerhalb der Sekundärzone erzeugen. Die von Zone B abgedeckten Bereiche werden durch zwei gekrümmte Seiten und eine flache Basis um die Außenseiten von Zone C herum begrenzt. In diesem Fall, Es entsteht eine fünfeckige Druckfläche, und nur eine Ecke des Fundaments verliert den Kontakt zum Boden. Jedoch, Die unten bereitgestellten Lösungen sind etwas komplex und erfordern numerische Lösungsverfahren für die Eckdrücke und x & y-Achsenabschnitte des Druckbereichs.

Eckdrücke (Schön & Verfolgen, 2017):

 

 

 

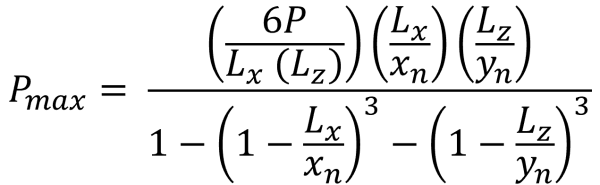
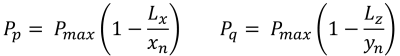
Fünfeckige Seiten des Druckbereichs (Schön & Verfolgen, 2017):

 

 

 

 

 

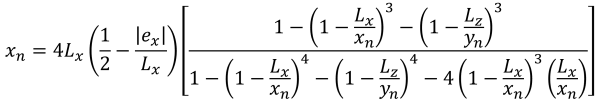
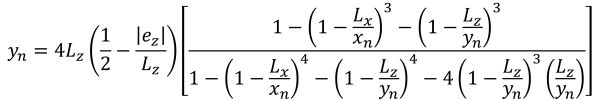
Eckdrücke basierend auf Exzentrizität
	P.1	P.2	P.3	P.4
ex(+), emit(+)	P.max	P.q	0	P.p
ex(+), emit(-)	P.p	P.max	P.q	0
ex(-), emit(-)	0	P.p	P.max	P.q
ex(-), emit(+)	P.q	0	P.p	P.max

 

Alternative, eine direktere Lösung von S.S. Strahl (1995) kann für die Eckdrücke und Schnittpunkte der fünfeckigen Druckzone verwendet werden. Die Gleichungen sind unten angegeben:

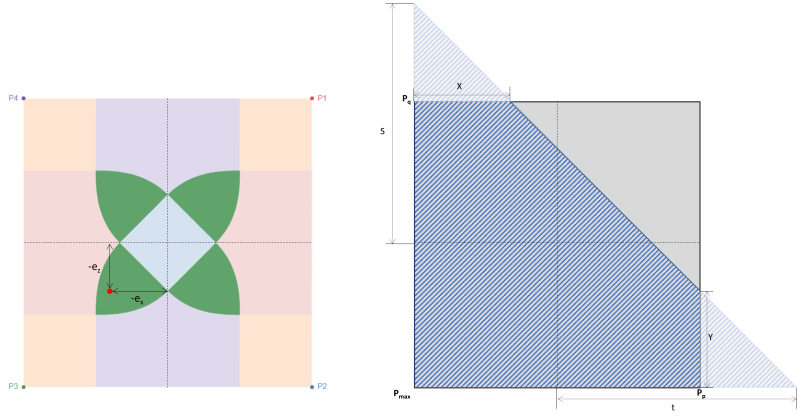
Eckdrücke (S.S. Strahl, 1995):

 

 

 

 

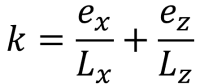
Fünfeckige Seiten des Druckbereichs (S.S. Strahl, 1995):

 

 

---

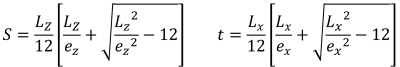
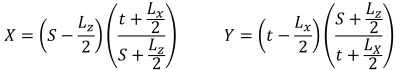
SkyCivs Modul „Foundation Design“. ist in der Lage, die Grunddrücke eines rechteckigen Betonfundaments zu lösen. Zusätzliche Designprüfungen gemäß verschiedenen Designvorschriften (ACI 318-14, Australischer Standard 2009 & 2018, Eurocode, und kanadische Standards) sind ebenfalls verfügbar.

Neuestes Update

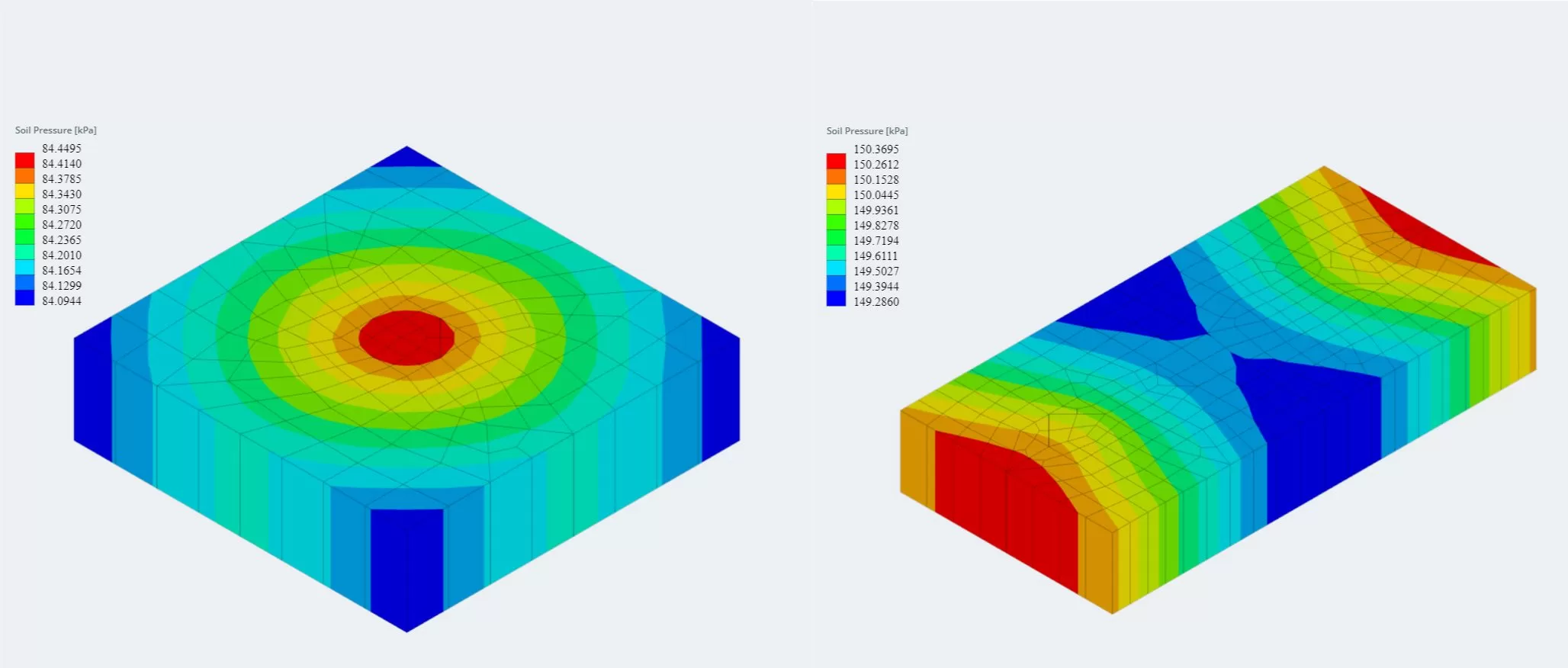
Die neueste Version des Grundlagenmoduls ist jetzt in die Finite-Elemente-Analyse integriert (HÄSSLICH), Dies bietet eine leistungsfähigere Bodendruckanalyse und führt eine Holzarmierungsanalyse ein, die für eine viel detailliertere Biegeprüfung verwendet werden kann. FEA-Ergebnisse für den Bodendruck und die Holzarmmomente können in 3D angezeigt werden und wurden den Berichten hinzugefügt.

 

Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Unser kostenloses Tool ermöglicht Benutzern die Durchführung Betonfundamentberechnungen ohne Download oder Installation!

Kostenloser Betonfundamentrechner

Verweise:

• Schön, J., Verfolgen, N.. (2017). Komplette analytische Lösung für die lineare Bodendruckverteilung unter einem starren, rechteckigen Fundament.
• Das, B.M. (2007). Grundlagen des Grundbaus (7th Ausgabe). Globales Engineering
• Rawat, S., et. al. (2020). Isolierte rechteckige Fundamente unter biaxialer Biegung: Eine kritische Bewertung und vereinfachte Analysemethodik.
• Strahl, S.S. (1995). Bewehrter Beton. Blackwell-Wissenschaft