Ein Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind. Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind, Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind. Ein Träger, Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind, Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind, Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind. Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind, Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind.

Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind (ACI 318).

Möchten Sie die Foundation Design-Software von SkyCiv ausprobieren?? Unser kostenloses Tool ermöglicht es Benutzern, Tragfähigkeitsberechnungen durchzuführen, ohne dass ein Download oder eine Installation erforderlich ist!

Foundation Design Calculator

Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind

Abmessungsanforderungen

Um die Abmessungen eines isolierten Fundaments zu bestimmen, Service oder nicht faktorisierte Lasten, wie tot (D.), Verkehrslast (L.), Wind (W.), Seismisch (E.), usw. werden mit Lastkombinationen angewendet, wie von ACI . definiert 318-14. Welche Lastkombination vorherrscht, wird als Bemessungslast betrachtet, und wird mit dem zulässigen Bodendruck verglichen, wie in Gleichung . gezeigt 1, wie empfohlen in Sektion 13.2.6 von ACI 318-14.

\(\Text{q}_{\Text{ein}} = frac{ \Text{Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind}_{\Text{n}} + \Text{Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind}_{\Text{n}} }{\Text{Ein}} \rechter Pfeil \) Gleichung 1

wo:
q_ein Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind
Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind_n Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind 1 (links)
Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind_n Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind 2 (richtig)
A = Fundamentfläche

Aus der Gleichung 1, q_ein sind im Austausch mit Ein.

\(\Text{Ein} = frac{ \Text{Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind}_{\Text{n}} + \Text{Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind}_{\Text{n}} }{\Text{q}_{\Text{ein}}} \rechter Pfeil \) Gleichung 1a

An dieser Stelle, die Abmessungen des Fundaments können aus dem benötigten Flächenmaß zurückgerechnet werden, Ein.

Einwegschere

Mit der Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind Grenzzustand, auch bekannt als “Biegeschere”, erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand “d” vom Gesicht einer Säule, erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand (Siehe Abbildung 1).

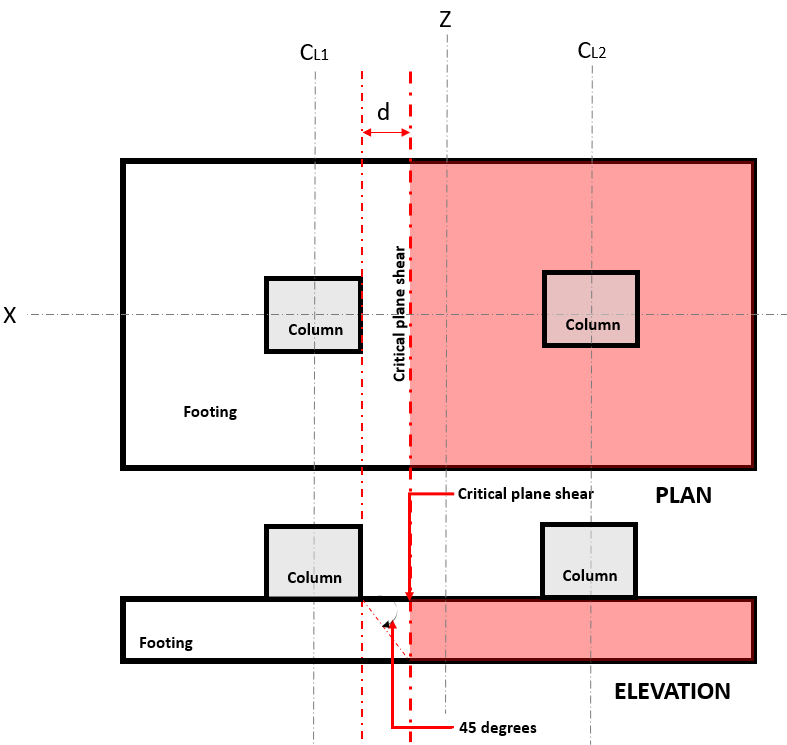
Abbildung 1. erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand

Mit der Einweg Scheren Nachfrage oder V _u wird unter der Annahme berechnet, dass das Fundament von der Stütze, in der sich die Fläche befindet, auskragt (rot) in Abbildung angegeben 1 in Übereinstimmung mit ACI 318-14, Sektion 8.5.3.1.1.

Mit der Einweg-Scherkapazität oder V_c ist als Bruchscherfestigkeit definiert und mit Gleichung . berechnet 2 pro ACI 318-14, Sektion 22.5.5.1:

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 2 \sqrt{\Text{F'}_{\Text{c}}} \mal text{b}_{\Text{w}} \mal text{d} \rechter Pfeil \) Gleichung 2 (ACI-Gl. 22.5.5.1 erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand)

oder

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 0.17 \sqrt{\Text{F'}_{\Text{c}}} \mal text{b}_{\Text{w}} \mal text{d} \rechter Pfeil \) Gleichung 2 (ACI-Gl. 22.5.5.1 Metrisch)

wo:
φ_Schub- = Schubbemessungsfaktor
f’_c = angegebene Betonfestigkeit, psi oder MPa
b_w = Dicke des Fundaments, in oder mm
d = Abstand von der Extremdruckfaser zum Schwerpunkt der Längszugbewehrung, in oder mm

Scherbedarf und Scherkapazität müssen die folgende Gleichung erfüllen, um die Konstruktionsanforderungen von ACI . zu erfüllen 318-14:

\(\Text{V }_{\Text{u}} \leq phitext{V }_{\Text{c}} \rechter Pfeil \) Gleichung 3 (ACI-Gl. 7.5.1.1(b))

SkyCiv-Stiftung, in Übereinstimmung mit Gleichung 3, berechnet das Einweg-Schereinheitsverhältnis (Gleichung 4) indem man den Scherbedarf über die Scherkapazität nimmt.

\( \Text{Verhältnis} = frac{\Text{Scherbedarf}}{\Text{Scherkapazität}} \rechter Pfeil \) Gleichung 4

Zwei-Wege-Schere

Mit der Zwei-Wege-Schere Grenzzustand, auch bekannt als “Stanzschere”, erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand. Die kritische Scherebene befindet sich in diesem Abschnitt des Fundaments (Siehe Abbildung 2).

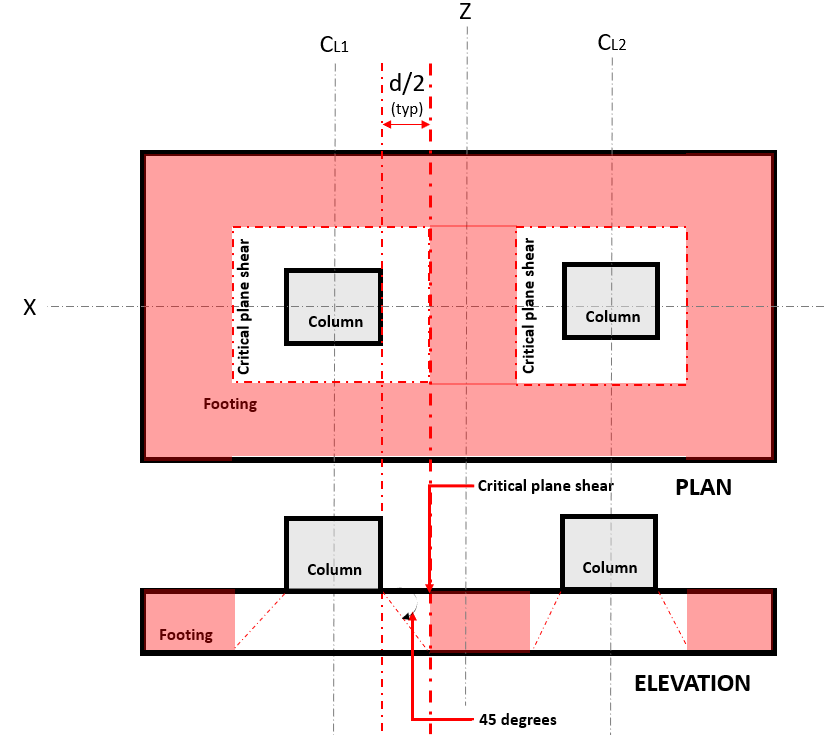
Abbildung 2. erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand

Mit der Zwei WegeNachfrage hören oder V _u tritt an der kritischen Scherebene auf, erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand (rot) schraffierter Bereich, in Abbildung angegeben 2, in Übereinstimmung mit ACI 318-14, Sektion 22.6.4.

Mit der Scherkapazität oder V_c richtet sich nach dem kleinsten mit Gleichung . berechneten Wert 5, 6, sowie 7 pro ACI 318-14, Sektion 22.6.5.2:

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 4 \mal lambda times sqrt{\Text{F'}_{\Text{c}}} \rechter Pfeil \) Gleichung 5 (ACI-Gl. 22.6.5.2(ein) erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand)

\(\phitext{V }_{\Text{c}} = links ( 2 + \frac{4}{\Beta } \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 6 (ACI-Gl. 22.6.5.2(b) erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand)

\(\phitext{V }_{\Text{c}} = left ( 2 + \frac{\alpha_{s} \mal d }{b{Das}} \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 7 (ACI-Gl. 22.6.5.2(c) erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand)

oder

\(\phitext{V }_{\Text{c}} = phi_{\Text{Schub-}} \mal 0.33 \mal lambda times sqrt{\Text{F'}_{\Text{c}}} \rechter Pfeil \) Gleichung 5 (ACI-Gl. 22.6.5.2(ein) Metrisch)

\(\phitext{V }_{\Text{c}} = 0.17 \mal links ( 1 + \frac{2}{\Beta } \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 6 (ACI-Gl. 22.6.5.2(b) Metrisch)

\(\phitext{V }_{\Text{c}} = 0.0083 \mal links ( 2 + \frac{\alpha_{s} \mal d }{b{Das}} \richtig ) \mal lambda times sqrt{f’_{c}} \rechter Pfeil \) Gleichung 7 (ACI-Gl. 22.6.5.2(c) Metrisch)

Hinweis: β ist das Verhältnis von langer Seite zu kurzer Seite der Säule, Einzellast, oder Reaktionsfläche und α_s erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand 22.6.5.3

wo:
λ = Modifikationsfaktor zur Berücksichtigung der reduzierten mechanischen Eigenschaften von Leichtbeton gegenüber Normalbeton gleicher Druckfestigkeit
f’_c = angegebene Betonfestigkeit, psi oder MPa
d = Abstand von der Extremdruckfaser zum Schwerpunkt der Längszugbewehrung, erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand

Scherbedarf und Scherkapazität müssen die folgende Gleichung erfüllen, um die Konstruktionsanforderungen von ACI . zu erfüllen 318-14:

\(\Text{V }_{\Text{u}} \leq phitext{V }_{\Text{c}} \rechter Pfeil \) Gleichung 8 (ACI-Gl. 7.5.1.1(b))

SkyCiv-Stiftung, in Übereinstimmung mit Gleichung 8, berechnet das Zwei-Wege-Schereinheitsverhältnis (Gleichung 9) indem man den Scherbedarf über die Scherkapazität nimmt.

\( \Text{Verhältnis} = frac{\Text{Scherbedarf}}{\Text{Scherkapazität}} \rechter Pfeil \) Gleichung 9

Biegung

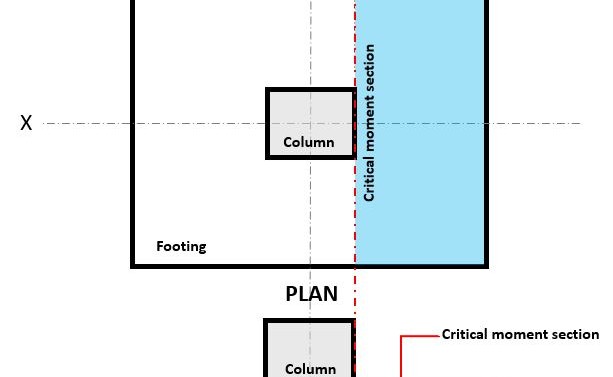
Abbildung 3. erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand

Mit der Biege Grenzzustand tritt ein bei der kritische Biegeabschnitt, befindet sich an der Stirnseite der Stütze oben auf dem Fundament (Siehe Abbildung 3).

Mit der Biegebedarf, oder M._u befindet sich in der Critical Flexure Section (blauer Lukenbereich) in Abbildung angegeben 3, und wird mit Gleichung . berechnet 10:

\( \Text{M.}_{u} = text{q}_{u} \mal links ( \frac{l_{x}}{2} – \frac{c_{x}}{2} \richtig ) \mal l_{mit} \mal links ( \frac{\frac{l_{x}}{2} – \frac{c_{x}}{2} }{2} \richtig ) \rechter Pfeil \) Gleichung 10

wo:
q_u = faktorisierter Bodendruck, ksf oder kpa
l_x = Fundamentmaß parallel zur x-Achse, in oder mm
l_mit = Fundamentmaß parallel zur z-Achse, in oder mm
c_x erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand, in oder mm

Mit der Biegekapazität, oder erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand wird mit Gleichung berechnet 11:

\( \phitext{M.}_{n} = phi_{\Text{Biegung}} \mal A_{s} \mal f_{und} \mal links( d – \frac{ein}{2} \richtig) \rechter Pfeil \) Gleichung 11

wo:
ϕ = Biegebemessungsfaktor
l_x = Fundamentmaß parallel zur x-Achse, in oder mm
l_mit = Fundamentmaß parallel zur z-Achse, in oder mm
d = Abstand von der Extremdruckfaser zum Schwerpunkt der Längszugbewehrung, in oder mm
Ein_s = Verstärkungsbereich, im² oder mm²
a = Tiefe des äquivalenten rechteckigen Spannungsblocks, in oder mm
erstreckt sich der kritische Abschnitt über die Breite des Fundaments und befindet sich in einem Abstand, ksi oder MPa

Verweise

1. Bauvorschriften für Konstruktionsbeton (ACI 318-14) Kommentar zu baurechtlichen Anforderungen an tragenden Beton (ACI 318R-14). Amerikanisches Betoninstitut, 2014.
2. McCormac, Jack C., und Russell H. Braun. Bemessung von Stahlbeton ACI 318-11 Code-Edition. Wiley, 2014.
3. Taylor, Andreas, et al. The Reinforced Concrete Design Handbook: ein Begleiter zu ACI-318-14. Amerikanisches Betoninstitut, 2015.