Como calcular as forças axiais de um sistema de treliça usando o método das juntas?
Neste tutorial, vamos explicar como usar o método de juntas para calcular as forças internas do membro em um sistema de treliça ou estrutura.
Essas forças são conhecidas como forças axiais e são muito importantes na análise de treliça. Se você não tem certeza sobre o que uma treliça é vista em nosso artigo – O que é uma treliça. O Método das Juntas envolve basicamente olhar para cada uma das 'juntas’ (onde os membros se encontram) e aplicando equações estáticas para resolver.
A grande coisa é, SkyCiv Truss faz isso automaticamente para você. Modele suas próprias treliças e o software mostrará passo a passo interativo trabalhando fora do método de juntas!
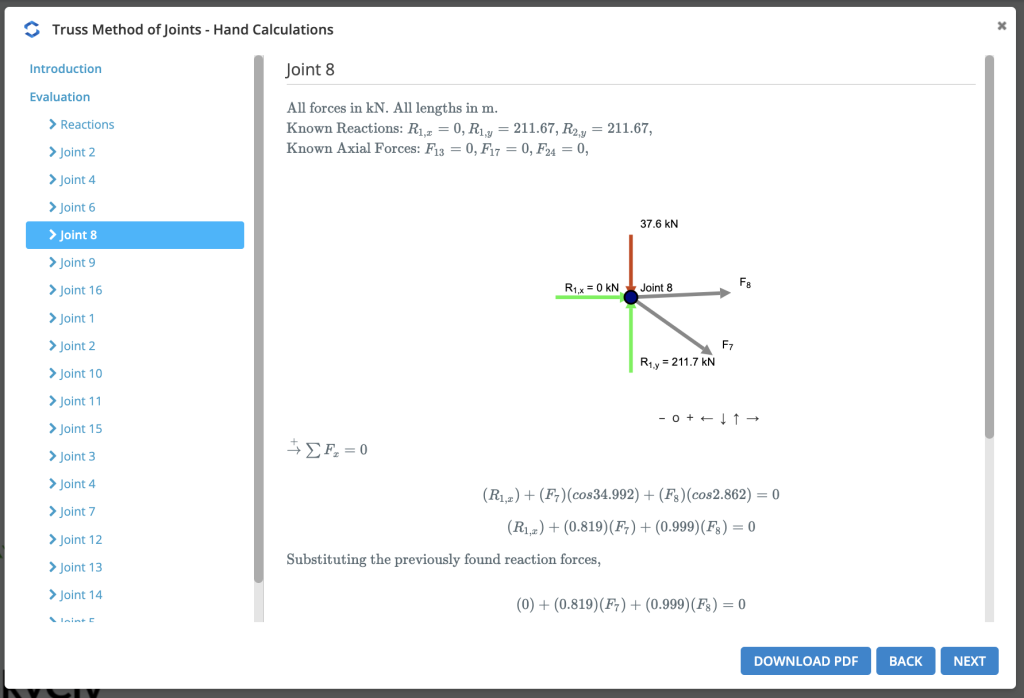
Passo 1: Calcule as reações nos apoios
Primeiro, nós calculamos o reações nos suportes. Começaremos examinando um exemplo simples de um 5 sistema de treliça de membro:
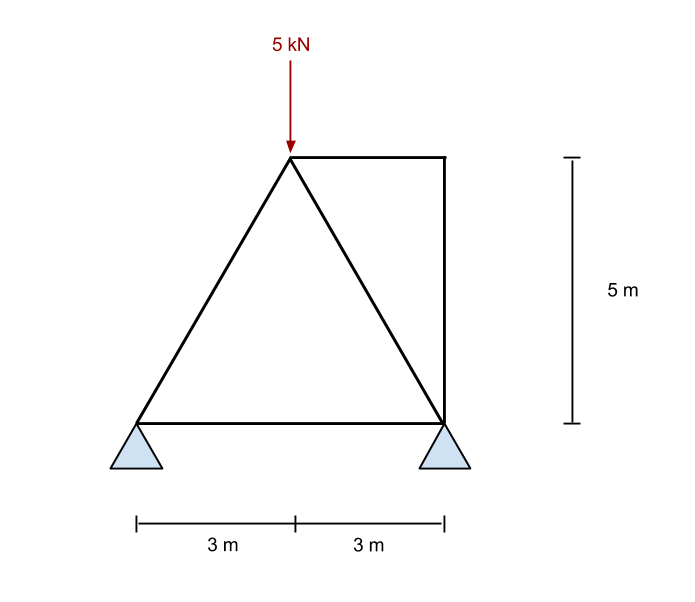
Para calcular o momentos de flexão neste sistema de treliça, primeiro consideramos a soma dos momentos na reação à esquerda como zero. Fazemos isso ignorando todos os membros e apenas olhando para as forças e apoios na estrutura. Este é o mesmo método usado nas reações de momento de flexão em nosso tutorial anterior.
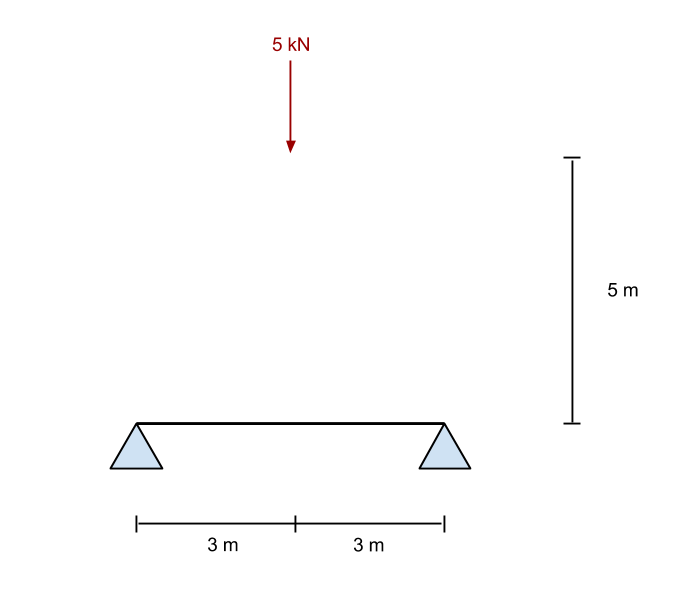
Das equações acima, resolvemos para a força de reação no ponto B (o suporte certo). Em nosso exemplo, Isso funciona para ser 2.5 kN em uma direção para cima. Agora, se tomarmos a soma das forças no y (vertical) direção, encontramos esse suporte A (o suporte esquerdo) também é dado como 2.5 kN.
Passo 2: Considere um dos suportes:
Agora que temos as forças de reação, podemos começar a análise do resto desta estrutura de treliça. em primeiro lugar, olhamos para uma de nossas forças conhecidas – nesse caso, vamos considerar a reação de suporte esquerdo de +2.5 kN. Uma vez que sabemos que esta força ocorre neste ponto, vamos considerar apenas este ponto isoladamente. Repetimos este processo várias vezes, por isso é importante praticar e aprender o processo para ter uma boa compreensão de como resolver as forças axiais em estruturas de treliça. Então novamente, considere o primeiro ponto no suporte:
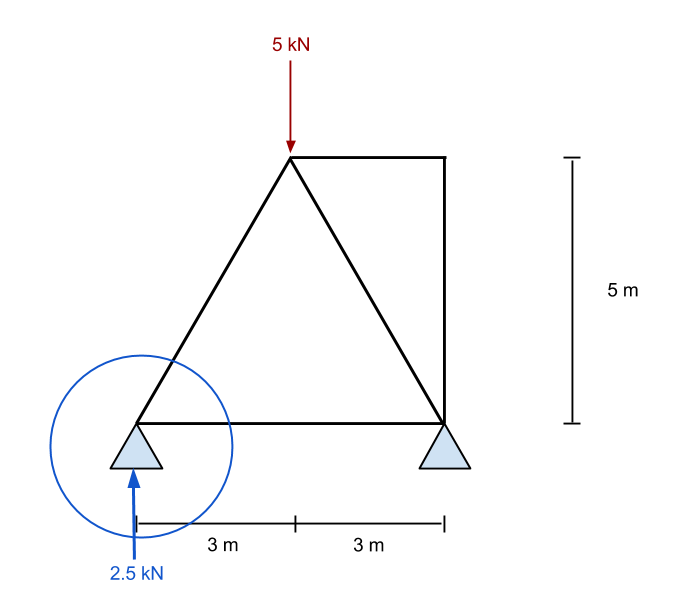
Aproximando este ponto, vemos todas as forças conhecidas agindo neste ponto. De estática, sabemos que as forças na direção xey devem somar zero. De acordo, se sabemos que existe uma força vertical ascendente, então deve haver uma força descendente para neutralizá-lo. Uma vez que já temos o valor de uma força voltada para cima, então tentaremos avaliar o número de membro 1 primeiro.
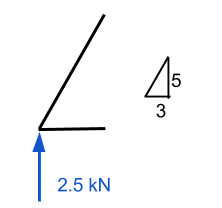
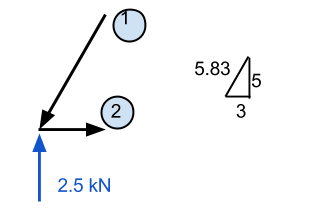
Aqui, exigimos algum conhecimento de vetores. É importante lembrar que todas as forças devem somar zero para as direções x e y. Em nosso exemplo, a distância horizontal é de 3m enquanto a vertical é de 5m – deixando-nos com a hipotenusa igual a aproximadamente 5.83 m. Usando este, podemos deduzir que o componente de força normal do membro 1 é igual a (5.83)/(5) vezes a força vertical de 2.5 kN. Isso equivale a 2.92 kN e DEVE ser uma força atuante para baixo se o ponto deve permanecer estacionário.
Membro 2 pode ser calculado da mesma maneira. Se conhecermos esse membro 1 está agindo para baixo, então sabemos que também deve agir para a esquerda. De acordo, nós conhecemos membro 2 deve estar gerando uma força que está puxando o ponto para a direita para manter as forças na direção x. Este valor é calculado por (3/5.83) x 2.92 kN e é igual a 1.51 kN.
Passo 3: Mova para outro ponto:
Tendo calculado as forças internas do primeiro membro em nossa treliça, vamos agora olhar para outro ponto para repetir o processo:
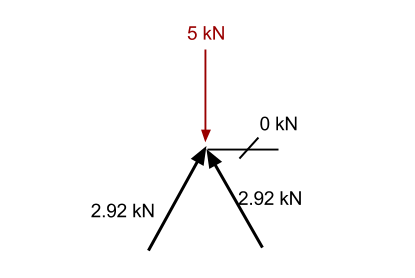
Novamente, vamos ampliar o ponto de referência e considerar todas as forças conhecidas atuando no ponto:
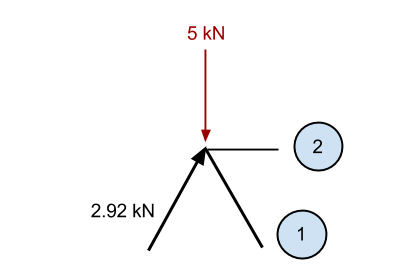
Da mesma forma que antes, se somarmos o componente vertical conhecido do 2.92 membro kN (2.5 kN na direção vertical) e o – 5força descendente kN, então temos excesso na direção descendente de 2.5 kN (5 – 2.5). De acordo, nós conhecemos aquele membro 1 deve estar causando uma força na direção para cima para manter o ponto estático. Esta força deve ter um componente vertical de 2.5 kN, e uma vez que está no mesmo ângulo do membro anterior, então a força axial interna também deve ser 2.92 kN.
Agora consideramos as forças na direção x. Neste ponto, toda a força vertical do membro 1 está resistindo à força vertical do membro calculado anteriormente. Isso significa que a soma das forças na direção x já é zero. De acordo, não pode haver força no Membro 2 ou então o ponto ficará desequilibrado e não mais estático.
Passo 4: Mova para outro ponto:
Olhando para este ponto, podemos ver que há um caso especial. Nesta situação, qualquer força empurrando para cima não terá ação de resistência possível, como não há outro membro que seja capaz de fornecer uma força para baixo para manter o ponto estático. De acordo, uma vez que a soma das forças deve ser zero, esse membro não pode ter nenhuma força associada a ele. Isto, Portanto, não tem força nele e é conhecido como Membro Zero.
Novamente, se olharmos para a soma das forças na direção x, podemos ver que há apenas um membro que tem alguma força na direção x. De acordo, isso também deve ter 0 força axial para que a soma das forças seja igual a zero.
Solução final
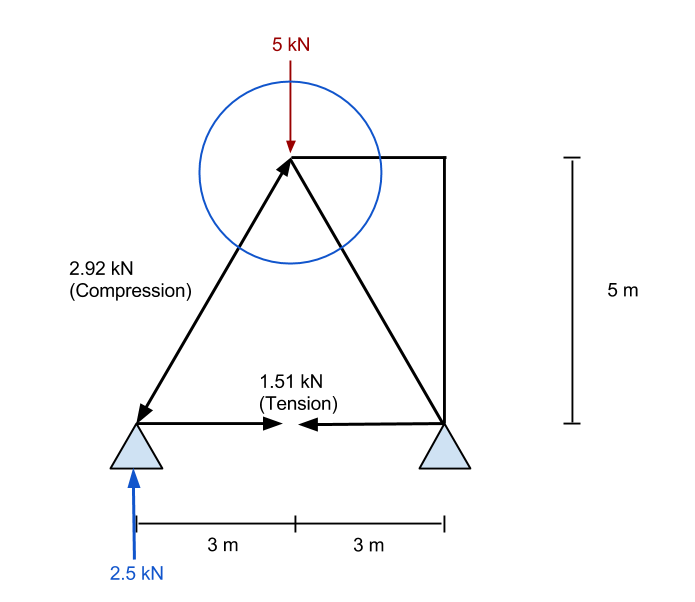
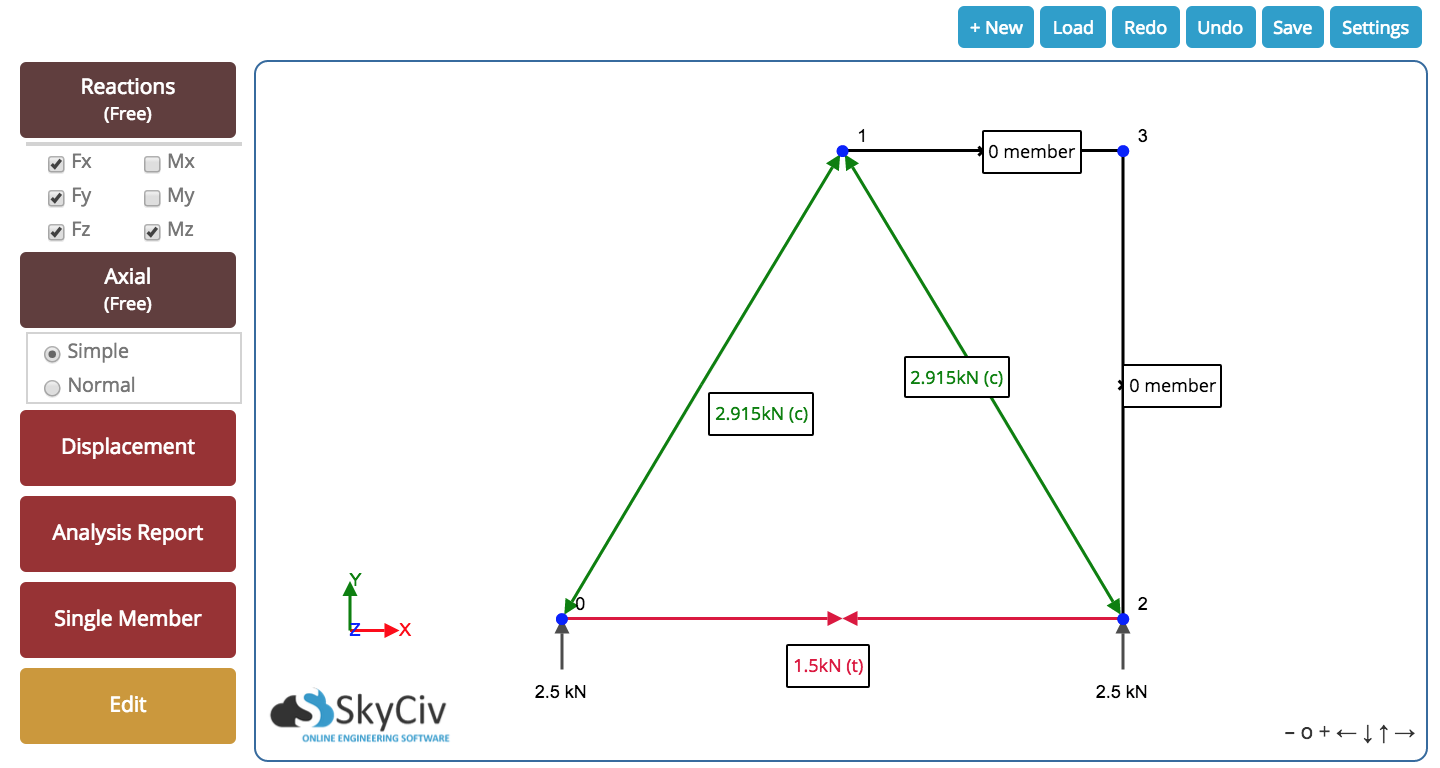
Finalmente, acabamos com o seguinte resultado para nossa treliça. Podemos ver todas as forças axiais resultantes dentro do membro e o reações nos suportes. O seguinte resultado foi retirado de nosso Calculadora Truss grátis – dê uma chance, é grátis!
Passos Simples
- Sempre comece calculando as reações nos apoios
- Escolha um ponto com uma força conhecida e observe-o isoladamente
- Use a geometria vetorial e a soma das forças = 0 para resolver as outras forças membro
- Repita o processo até que todos os membros estejam resolvidos
- Lembre-se de olhar para Zero Members
Tutorial relevante
- Resolvendo treliças pelo método das seções. Inclui um vídeo e um guia passo a passo
SkyCiv Truss
SkyCiv Truss pode calcular o método de juntas automaticamente para você. Ou experimente o nosso Calculadora Truss grátis que lhe dará a resposta final (sem cálculos manuais).
Para explorar mais funcionalidades do software SkyCiv, inscreva-se hoje para começar!
