Um guia para os cálculos necessários para projetar uma sapata isolada (EN 1992 & EN 1997)
A fundação é um sistema de construção essencial que transfere as forças da coluna e da parede para o solo de suporte. Dependendo das propriedades do solo e cargas da construção, o engenheiro pode optar por apoiar a estrutura em um sistema de fundação raso ou profundo³.
A SkyCiv Foundation inclui o projeto de sapata isolada em conformidade com o Eurocódigo 2¹ e o Eurocódigo 72.
Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta permite que os usuários realizem cálculos de Foundation Design sem nenhum download ou instalação!
Parâmetros de projeto de uma sapata isolada
Os cálculos apresentados no SkyCiv utilizam o método prescritivo baseado em EN 1997, onde uma pressão de suporte segura assumida é usada para dimensionar a fundação com base no estado limite de utilização seguida pelo projeto estrutural detalhado com base no estado limite último.
Requisitos de Dimensão
Para determinar as dimensões de uma sapata isolada, ações características, como Permanente/Morto (Q), Variável/Ao vivo (Ql), Vento (Qw), Sísmica (Qe), etc serão aplicados para o estado limite de utilização. O arranjo/combinação de carga crítica será considerado a carga de projeto, e é comparado com a pressão do solo permitida, conforme mostrado na Equação 1. Este exemplo é limitado apenas à pressão uniforme do solo.
\(\texto{q}_{\texto{uma}} = frac{\texto{P}_{\texto{n}}}{\texto{A}} \seta direita \) Equação 1
Onde:
quma = pressão permitida do solo
Pn = carga de projeto não fatorada
A = área da fundação
Da Equação 1, quma são intercâmbio com A.
\(\texto{A} = frac{\texto{P}_{\texto{n}}}{\texto{q}_{\texto{uma}}} \seta direita \) Equação 1a
Neste ponto, as dimensões da base podem ser calculadas retroativamente a partir da dimensão da área necessária, A.
Flexure
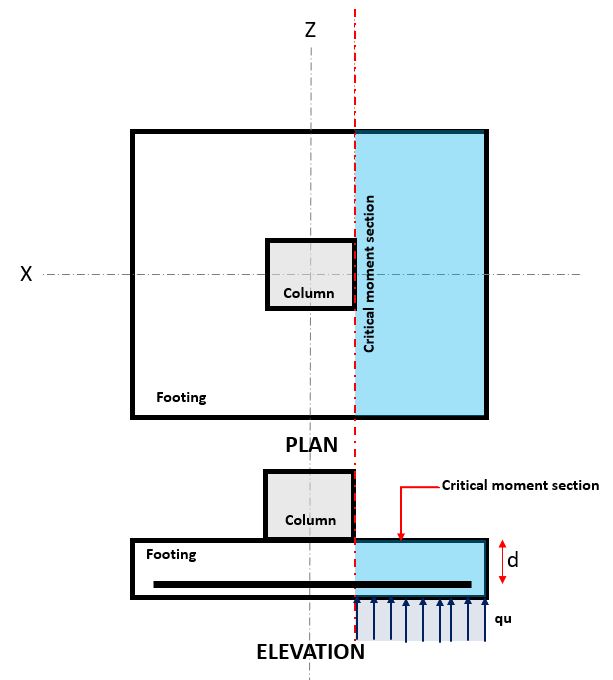
Figura 1. Seção Crítica de Flexão
A Flexural estado limite ocorre em a seção de flexão crítica, localizado na face da coluna no topo da sapata (Consulte a Figura 1).
A Demanda Flexural, ou MDE está localizado na Seção de Flexão Crítica (área de hachura azul) indicado na figura 1, e é calculado usando a Equação 2.
\( \texto{M}_{você} = text{q}_{você} \times left ( \fratura{eu_{x}}{2} – \fratura{c_{x}}{2} \direito ) \vezes l_{z} \times left ( \fratura{\fratura{eu_{x}}{2} – \fratura{c_{x}}{2} }{2} \direito ) \seta direita \) Equação 2
Onde:
qvocê = pressão do solo fatorada, kPa
eux = dimensão da base ao longo do eixo x, milímetros
euz = dimensão da base ao longo do eixo z, milímetros
cx = dimensão da coluna ao longo do eixo x, milímetros
A Capacidade Flexural, ou MUm guia para combinações de carga Eurocode é calculado usando a Equação 3.
\(\texto{M}_{Um guia para combinações de carga Eurocode} = frac{1}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{S,ponto}} \vezes f_{sim} \vezes A_{s} \times left( d – \fratura{s}{2} \direito) \seta direita \) Equação 3
Onde:
cS,ponto = fator parcial para aço de reforço
eux = dimensão da sapata paralela ao eixo x, milímetros
euz = dimensão da sapata paralela ao eixo z, milímetros
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, milímetros
As = área de reforço, milímetros2
s = profundidade do bloco de tensão retangular equivalente, milímetros
fyk = resistência do reforço, MPa
A demanda de momento e a capacidade de momento devem ser verificadas para atender ao estado limite último de EN 1990:
\(\texto{E}_{\texto{d}} \leq texto{R}_{\texto{d}} \seta direita \) Equação 4 (EN 1990 6.4.1)
Fundação SkyCiv, em conformidade com a Equação 4, calcula a razão da unidade de flexão (Equação 5) tomando Flexural Demand em vez de Flexural Capacity.
\( \texto{Razão de Unidade} = frac{\texto{Flexure Demand}}{\texto{Capacidade de Flexão}} \seta direita \) Equação 5
Tesoura unidirecional
A cisalhamento unidirecional estado limite, também conhecido como cisalhamento de feixe, está localizado a uma distância “d” da face de uma coluna, no plano de cisalhamento crítico (Consulte a Figura 2),
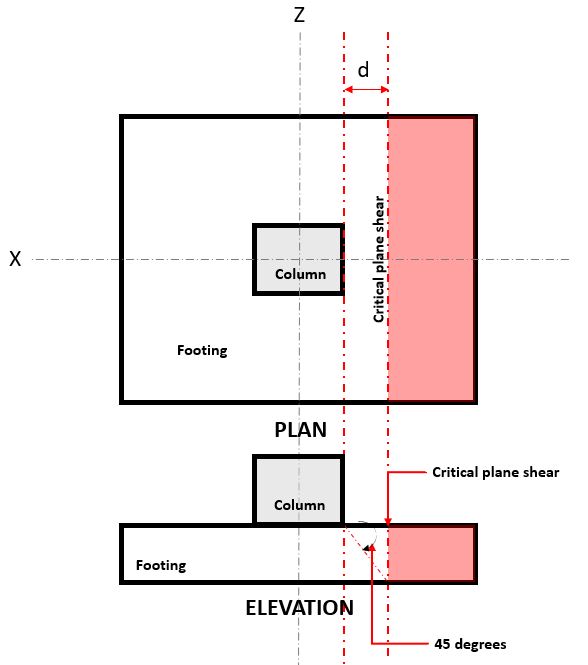
Figura 2. Cisalhamento plano crítico de cisalhamento unidirecional
A Mão única Cisalhamento Demanda ou VDE é calculado assumindo que a sapata está em balanço longe da coluna onde a área é (vermelho) indicado na figura 2.
A Capacidade de cisalhamento unilateral ou VRd,c é definida como a resistência ao cisalhamento no estado limite último (quando nenhuma armadura de cisalhamento é necessária) e calculado usando a equação 6 por EN 1992, Seção 6.2.2.
\(\texto{V}_{\texto{Rd,c}} = (\texto{C}_{\texto{Rd,c}} \vezes k vezes (100 \vezes rho_{1} \times text{f}_{\texto{inclui cálculos detalhados passo a passo}})^{\fratura{1}{3}}) \times text{b}_{\texto{C}} \times text{d} \seta direita \) Equação 6 (EN 1992 Eq. 6.2.uma)
com um mínimo de
\(\texto{V}_{\texto{Rd,c}} = (0.035 \vezes k^{\fratura{3}{2}} \times text{f}_{\texto{inclui cálculos detalhados passo a passo}}^{\fratura{1}{2}}) \times text{b}_{\texto{C}} \times text{d} \seta direita \) Equação 9 (EN 1992 Eq. 6.2.b)
Onde:
CRd,c = valor recomendado de 0,18/γC
k = coeficiente de 1 + √(200/d) ≤ 2.0
ρ1 = Asl / bCd ≤ 0.02
finclui cálculos detalhados passo a passo = resistência do concreto especificada, MPa
bC = largura da base, milímetros
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, milímetros
A demanda de cisalhamento e a capacidade de cisalhamento devem ser verificadas para atender ao estado limite último da EN 1990:
\(\texto{E}_{\texto{d}} \leq texto{R}_{\texto{d}} \seta direita \) Equação 4 (EN 1990 6.4.1)
Fundação SkyCiv, em conformidade com a Equação 4, calcula a razão de unidade de cisalhamento unilateral (Equação 7) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Razão de Unidade} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 7
Cisalhamento de duas vias
A Cisalhamento de duas vias estado limite, também conhecido como punção, estende a seção crítica a uma distância “2d” da face da coluna e ao redor do perímetro da coluna. O Plano de Cisalhamento Crítico está localizado nessa seção da sapata (Consulte a Figura 3).
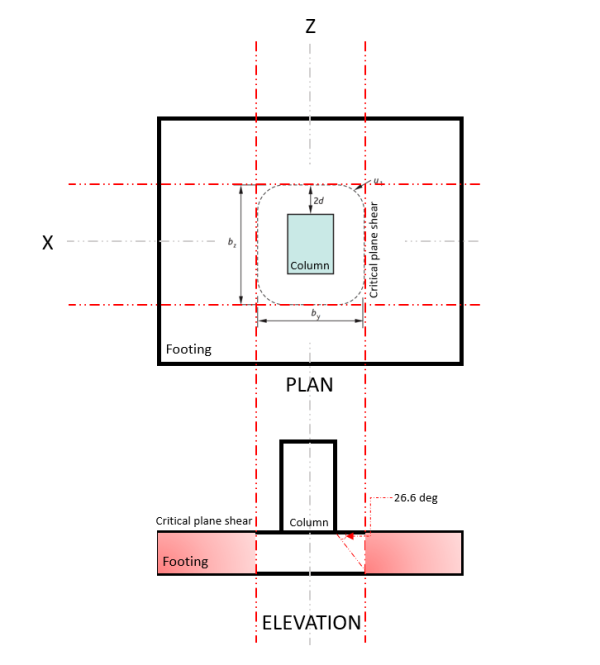
Figura 3. Plano de cisalhamento crítico de cisalhamento bidirecional
A Dois caminhosouvir Demanda ou VDE ocorre no plano de cisalhamento crítico, indicado na figura 3, de acordo com EN 1992, Seção 6.4.2.
A Capacidade de cisalhamento ou VRd,c, semelhante à capacidade de cisalhamento unidirecional (quando nenhuma armadura de cisalhamento é necessária), é calculado com base em EN 1992 Seção 6.2.2 (Consulte a equação. 8).
\(\texto{V}_{\texto{Rd,c}} = (\texto{C}_{\texto{Rd,c}} \vezes k vezes (100 \vezes rho_{1} \times text{f}_{\texto{inclui cálculos detalhados passo a passo}})^{\fratura{1}{3}}) \times text{você}_{\texto{1}} \times text{d} \seta direita \) Equação 8 (EN 1992 Eq. 6.2.uma)
com um mínimo de
\(\texto{V}_{\texto{Rd,c}} = (0.035 \vezes k^{\fratura{3}{2}} \times text{f}_{\texto{inclui cálculos detalhados passo a passo}}^{\fratura{1}{2}}) \times text{você}_{\texto{1}} \times text{d} \seta direita \) Equação 9 (EN 1992 Eq. 6.2.b)
Onde:
você1 = perímetro de controle básico, milímetros
Outras variáveis definidas de forma semelhante em Capacidade de cisalhamento unidirecional.
No geral, A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender ao estado limite último da EN 1990:
\(\texto{E}_{\texto{d}} \leq texto{R}_{\texto{d}} \seta direita \) Equação 4 (EN 1990 6.4.1)
Fundação SkyCiv, em conformidade com a equação 4, calcula a razão da unidade de cisalhamento bidirecional (Equação 10) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Razão de Unidade} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 10
NOVA Fundação SkyCiv com FEA
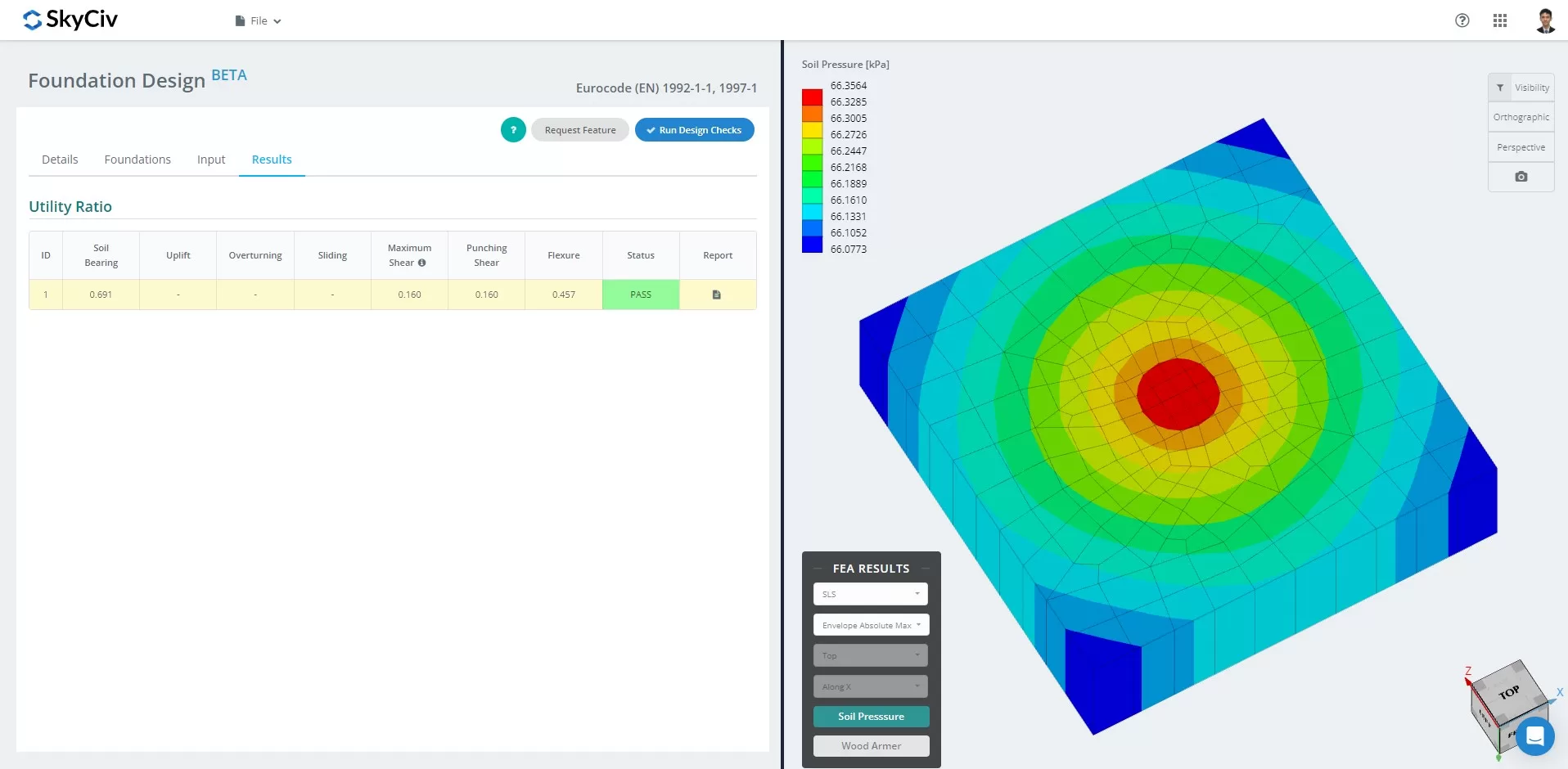
A partir de março 2024, o Módulo Foundation Design integrou a Análise de Elementos Finitos (FEIO) solucionador em suas capacidades. Este novo recurso permite que os usuários realizem análises aprofundadas da pressão do solo e da armação de madeira, ao mesmo tempo em que realizam todas as verificações estruturais especificadas pela EN. 1992 e 1997, incluindo todas as verificações mencionadas acima. O resumo dos resultados da FEA está incluído no relatório abrangente.
Calculadora grátis para pés de concreto
Experimente a calculadora gratuita de sapatas de concreto SkyCiv para projetar fundações para sapatas, sapatas combinadas, estacas de concreto, almofadas de concreto, e mais.
Referências
- Eurocódigo 2: Projeto de estruturas de concreto – Papel 1-1: Regras gerais e regras para edifícios (EN 1992-1-1:2004). Comité Europeu de Normalização, 2004.
- Eurocódigo 7: Projeto geotécnico – Papel 1: Regras gerais (EN 1997-1:2004). Comité Europeu de Normalização, 2004.
- Mosley, Bungey, e Hulse. Projeto de concreto armado de acordo com o Eurocódigo 2 (Sétima Edição), 2012.
Desenvolvedor de Produto
bacharelado (Civil)


