Projeto de pilha única de acordo com ACI 318 (2014)

As estacas são membros longos e delgados que transferem as cargas da superestrutura para o solo mais profundo ou para uma rocha com capacidade de suporte adequada. Os materiais usados ​​para as pilhas podem incluir madeira, aço, e concreto. A instalação da estaca no solo pode ser conduzida, perfurado, ou jacked que são então conectados a blocos de pilha. Muitos fatores, como condições do site, tipo de solo, a transmissão de cargas, são considerados para classificar o tipo e instalação de estacas. Este artigo se concentrará no projeto de uma estaca de concreto de acordo com o American Concrete Institute (ACI) 318 – 2014.

O módulo SkyCiv Foundation Design inclui o projeto de estacas em conformidade com o American Concrete Institute (ACI 318) e padrões australianos (AS 2159 & 3600).

Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta gratuita permite que os usuários realizem cálculos de transporte de carga sem qualquer download ou instalação!

Calculadora de design de base

Capacidade de carga de uma pilha

Geralmente, as cargas verticais aplicadas nas estacas são suportadas pelo rolamento da extremidade da estaca, e a resistência à fricção da pele desenvolvida ao longo de seu comprimento. A capacidade máxima de carga (Q_você) deve ser representado pela equação (1). Um fator de segurança é aplicado para calcular a capacidade de carga permitida (Q_A).

\({Q}_{você} = {Q}_{p} + {Q}_{s}\) (1)

Q_você = Capacidade máxima de carga

Q_P = Resistência do rolamento de extremidade

Q_S = Resistência à fricção da pele

\({Q}_{A} = frac{{Q}_{você}}{FOS} \) (2)

Q_A = Capacidade de carga permitida

FOS = Fator de segurança

Para um guia mais detalhado, confira nosso artigo sobre cálculo a resistência à fricção da pele e a capacidade de suporte da extremidade.

Resistência estrutural de uma única estaca

As estacas também estão sujeitas a forças axiais, forças de corte, e momento de flexão, é por isso que eles são estruturalmente projetados de forma semelhante a colunas. Seção 10.5.1.1 afirma que toda a carga fatorada não deve exceder suas resistências de projeto correspondentes.

\( {øP}_{N} ≤ {P}_{você} \) (3uma)

\( {dolorido}_{N} ≤ {M}_{você} \) (3b)

\( {øV}_{N} ≤ {V}_{você} \) (3c)

P_você, M_você, V_você = Axial fatorado, momentos de flexão, cargas de cisalhamento

P_N, M_N, V_N = Axial nominal, momentos de flexão, cargas de cisalhamento

ø = Fatores de redução de força (Tabela 1)

Fatores de redução de força(ϕ)
Axial	0.65-0.90
Flexural	0.65-0.90
Cisalhamento	0.75

Tabela 1: Fatores de redução de força (Tabela 21.2.1, ACI 318-14)

Capacidade de cisalhamento de uma única pilha (øV_N)

A resistência ao cisalhamento nominal deve ser equivalente às contribuições combinadas das capacidades de cisalhamento do concreto e da armadura de aço.

Resistência ao cisalhamento do concreto (V_c)

A contribuição do concreto para a capacidade de cisalhamento é calculada conforme mostrado na equação (4) que é definido na Seção 22.5.5.1 de ACI 318-14.

\( {V}_{c} = 0.17 × λ × quadrado{fc ’} × b × d \) (4)

λ = Fator de modificação do concreto = 1 (Concreto de peso normal, Tabela 19.2.4.2)

fc’ = Resistência do concreto

b = largura ou diâmetro da pilha

d = 0.80 × profundidade da pilha (Seção 22.5.2.2)

Resistência ao cisalhamento de barras de aço (V_s)

A contribuição da armadura de cisalhamento lateral para a capacidade de cisalhamento é calculada como o mínimo entre as equações (5) e (6).

\( {V}_{s} = 0.066 [object Window]{fc ’} × b × d \) (5)

\( {V}_{s} = frac{{A}_{v} × {f}_{yt} × d }{s} \) (6)

A_V = Área das barras de reforço de cisalhamento

f_yt = Resistência ao escoamento das barras de reforço de cisalhamento

s = espaçamento centro a centro das barras de reforço de cisalhamento

Resistência ao cisalhamento nominal (øV_N)

Resumindo a saída da equação 4-6 deve resultar na resistência ao cisalhamento nominal da pilha. Fator de redução de força (ø) deve ser igual a 0.75 conforme definido na Tabela 22.2.1 de ACI 318-14.

\( {øV}_{N} = ø × ({V}_{c} + {V}_{s}) ≤ {øV}_{você} \) (7)

Calculadora de design de base

Capacidades axial e flexural de uma única estaca (øP_N, dolorido_N )

As capacidades axial e flexural são verificadas usando um diagrama de interação. Este diagrama é uma representação visual do comportamento das capacidades de flexão e axial causadas por um aumento na carga do ponto de flexão puro até que um ponto de equilíbrio seja alcançado.

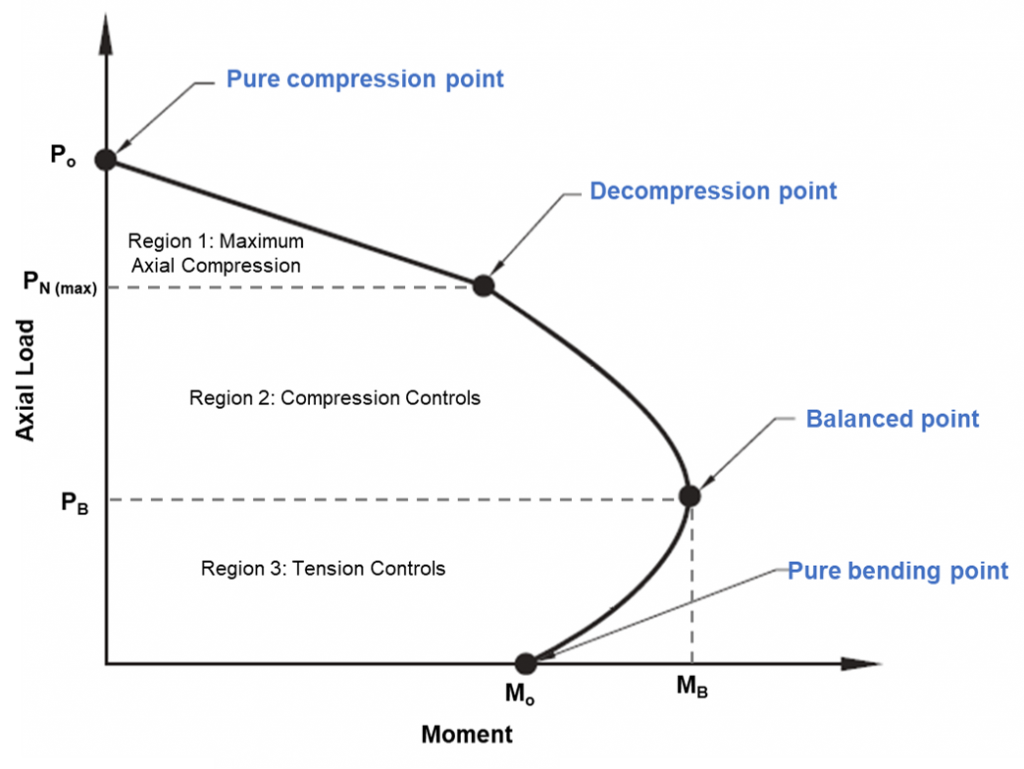
Figura 1: Diagrama de interação de coluna

Diagrama de interação de coluna

O ponto de compressão puro no diagrama é onde a pilha irá falhar na compressão puramente. Neste ponto, a carga axial é aplicada ao centroide de plástico da seção para permanecer em compressão sem dobrar. A resistência da pilha entre o ponto de compressão puro até os pontos de descompressão pode ser calculada por interpolação linear. O ponto de descompressão é onde a deformação do concreto na fibra compressiva extrema é igual a 0.003, e a deformação na fibra de tração extrema é zero. O ponto de flexão puro é onde a capacidade de carga axial é zero. Entre a transição do ponto de descompressão para o ponto de flexão puro, uma condição equilibrada é alcançada. Neste ponto, a deformação do concreto está no limite (e_c= 0,003), e a deformação externa do aço atinge o rendimento (e_s= 0,0025). Qualquer combinação de carga axial e momento de flexão fora do diagrama causará falha.

Resistência máxima à compressão axial nominal para o projeto (øP_N)

A resistência axial do projeto de uma seção deve ser limitada apenas a 80-85% da força axial nominal para levar em conta a excentricidade acidental.

\( {øP}_{N} = ø × {P}_{o} \) (8uma)

\( {P}_{o} = F × [0.85 × {f}_{c} × ({A}_{g} – {A}_{st}) + ({f}_{Y} × {A}_{st}) ] \) (8b)

F = 0.80 (Laços)

F = 0.85 (Espiral)

A_G = Área bruta da seção transversal da estaca

A_st = Área total das barras de aço longitudinais

f_Y = Resistência ao escoamento das barras de aço

Resistência à flexão nominal (dolorido_N)

A construção do diagrama de interação para a coluna envolve traçar uma série de valores de P_N e M_N. Valores para P_N deve ser equivalente à soma das forças de tração e compressão, como mostrado nas Figuras 2a e 2b, enquanto o M correspondente_N é calculado resolvendo essas forças sobre o eixo neutro. Essas forças incluem a força compressiva que atua na área de compressão e as forças exercidas por cada uma das barras de reforço que podem ser compressivas ou de tração. Um procedimento geral é sugerido abaixo para construir um diagrama de interação usando as equações apresentadas.

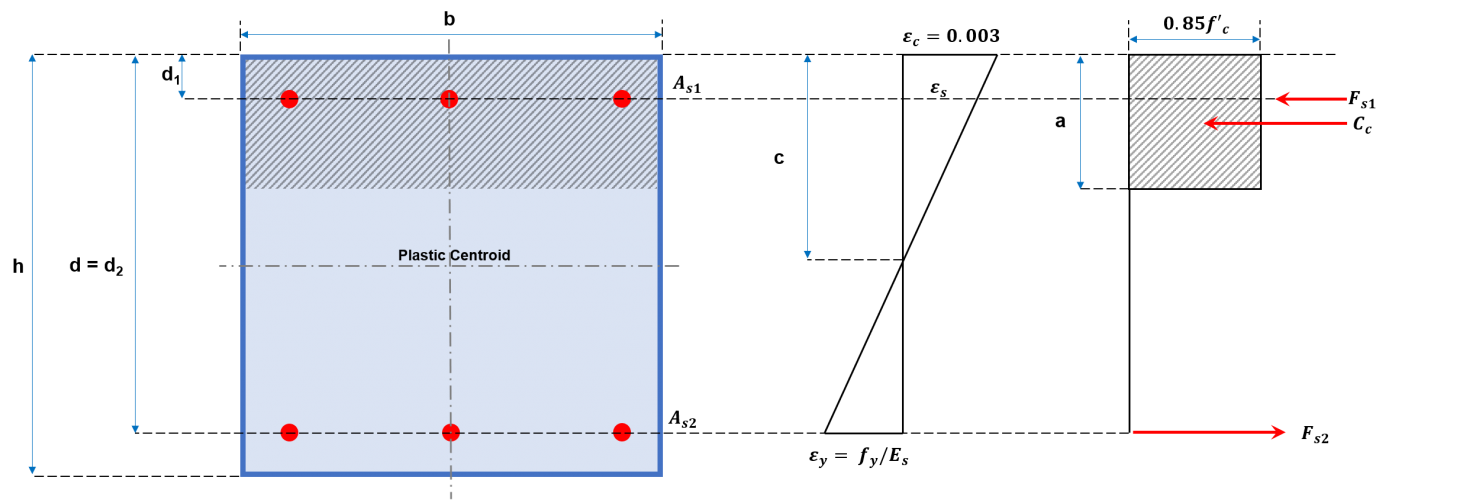
Figura 2a: Seção transversal de coluna retangular

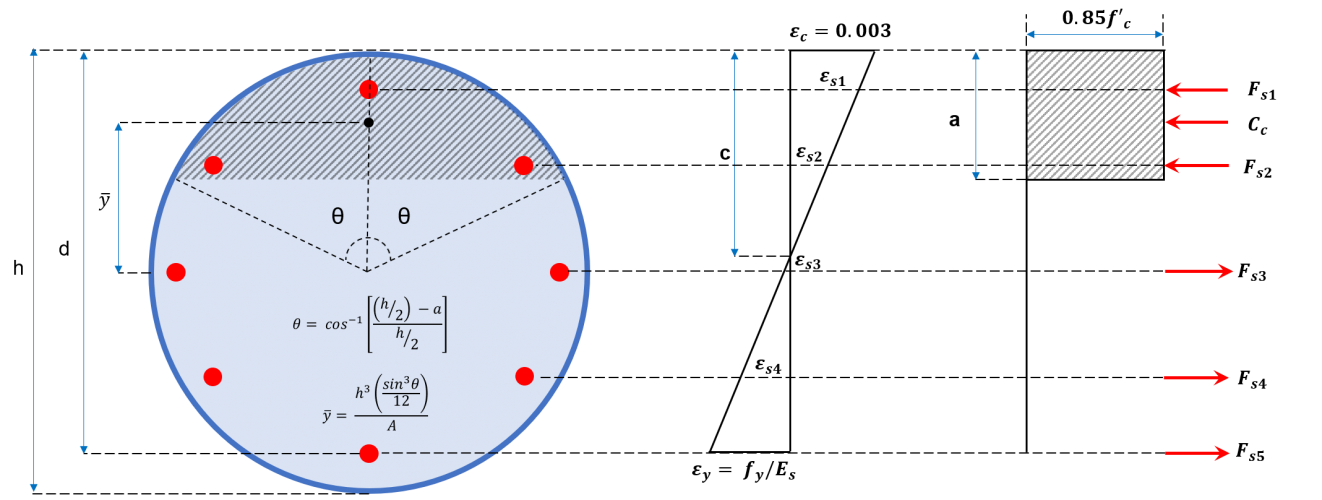
Figura 2b: Seção transversal da coluna circular

Procedimento geral para o diagrama de interação de uma coluna

(1) Calcule o valor de P_o e P_N (equações 8a e 8b).

(2) Determine ce as tensões nos reforços.

\( c = 0.003 [object Window]{{d}_{1}}{0.003 + (Z + {e}_{Y})} \) (9)

c = profundidade do eixo neutro

e_Y = Esforço de aço = f_Y/E_s

Z = valor arbitrário (0, -0.5, -1.0, -2.5)

Uma série de casos deve ser considerada selecionando vários locais do eixo neutro, c. Para definir as localizações do eixo neutro, diferentes deformações de aço devem ser selecionadas multiplicando um valor arbitrário Z para a tensão de escoamento do aço. Existe uma grande variedade de valores para Z. Contudo, existem apenas quatro pontos obrigatórios para usar no diagrama de interação.

• Z = 0: neste ponto, a deformação na camada extrema em tensão é zero. Este ponto marca a mudança da emenda sobreposta de compressão permitida em todas as barras longitudinais para uma emenda sobreposta de tensão.
• Z = -0.5: esta distribuição de tensão afeta o comprimento da emenda sobreposta de tensão em uma coluna & normalmente é plotado em um diagrama de interação.
• Z = -1: isso marca o ponto de uma condição equilibrada. Esta distribuição de deformações marca a mudança de falhas por compressão originadas pelo esmagamento da superfície de compressão da seção para falhas por tração iniciadas pelo escoamento da armadura longitudinal.
• Z = -2.5: este ponto corresponde ao limite de deformação controlada por tensão de 0.005.

(3) Calcule as tensões nas camadas de reforço.

\({f}_{e} ={e}_{e} × {E}_{s} \) (10)

f_e = Tensão no aço

e_e = Deformação no aço

\({e}_{e} = frac{c -{d}_{I}}{c} × 0.003 \) (11)

E_s = Módulo de elasticidade do aço

(4) Determine a altura do bloco de tensão de compressão, uma.

\(a = {b}_{1} × c \) (a ≤ h)(12)

Para f’c ≤ 4000 psi (28 MPa):

b₁ = 0.85

Para f’c > 4000 psi (28 MPa):

\( {b}_{1} = 0.85 – \fratura{0.05 × (f’c – 4000)}{1000} \) (Imperial)

\( {b}_{1} = 0.85 – \fratura{0.05 ×(f’c – 28)}{7} \) (Métrica)

(5) Calcule as forças em concreto e aço.

Área do bloco de estresse compressivo:

\({A}_{c} = a × b \) (Seção transversal retangular)

\({A}_{c} ={h}^{2} [object Window]{θ – senθ cosθ}{4} \) (Seção transversal circular)

Força compressiva em concreto:

\({C}_{c} = (0.85 × f’c) × {A}_{c}\) (14)

Força de tração no aço (d_I≤ a):

\({F}_{e} = {f}_{e} × {A}_{e} \) (15)

Força compressiva em aço (d_I > uma):

\({F}_{e} = [{f}_{e} – (0.85 × f’c)] × {A}_{e} \) (16)

(6) Calcule para a capacidade axial (P_N).

\({P}_{N} = {C}_{c} + Σ {F}_{e} \) (17)

(7) Calcule para a capacidade de flexão (M_N).

\({M}_{N} = [{C}_{c} × (\fratura{h}{2} – \fratura{uma}{2})]+ Σ [{F}_{e} × (\fratura{h}{2} – {d}_{I}) \) (18)

(8) Calcule o valor do fator de redução de força (ø).

Conforme mostrado na Tabela 1, o fator de redução de força para axial e flexão varia de 0.60 para 0.90. Seção 21.2 de ACI 318-14 demonstra seu valor no momento, força axial, ou momento e força axial combinados, como mostrado na Tabela 2 abaixo.

Classificação	Espiral	Amarrado
Compressão controlada	0.75	0.65
Transição de compressão para tensão	0.75 + [50 × (et – 0.003) ]	0.65 + [(250/3) × (et – 0.003) ]
Tensão controlada	0.90	0.90

Tabela 2: Fatores de redução de força para axial, momento ou combinar axial e momento (Tabela 21.2.2, ACI 318-14)

(9) Repita as etapas 2-8 com vários valores para Z.

(10) Trace no diagrama os valores de øP_N e øM_N.

Projeto de Estacas de Concreto com Calculadora Gratuita de Fundação SkyCiv

SkyCiv Free Foundation Calculator ajuda você com projeto de estacas de concreto e outras tarefas, como sapatas e projeto de estacas de concreto. Confira agora para explorar como nossa calculadora pode ajudá-lo com seu projeto de estacas de concreto!

Calculadora de design de base

Referências

• • Requisitos de Código para Concreto Estrutural (2014). AC! 318-14 American Concrete Institute.
  • Hsiao, J.K. (2012). Efeitos do eixo de flexão no momento de carga (PM) Diagramas de interação para colunas circulares de concreto usando um número limitado de barras de reforço longitudinais. Jornal Eletrônico de Engenharia Estrutural 12 (1). Obtido de http://www.ejse.org