Calculadora de momento de inércia e centroide
Calcule o momento de inércia, o centro de gravidade, e o módulo de seção para uma ampla variedade de seções
Este é um tutorial para nossa calculadora de momento de inércia
SkyCiv Moment of Inertia and Centroid Calculator ajuda a determinar o momento de inércia, centróide, e outras propriedades geométricas importantes para uma variedade de formas, incluindo retângulos, círculos, seções ocas, triângulos, vigas tipo I, vigas tipo T, ângulos e canais. Também temos alguns artigos abaixo sobre como calcular o momento de inércia, bem como mais informações sobre centroides e módulos de seção.
Você pode resolver até três seções antes de ser obrigado a se inscrever para uma conta gratuita - que também dá acesso a mais softwares e resultados. Nossa conta paga mostrará os cálculos manuais completos de como a ferramenta chegou a esse resultado. Consulte abaixo para mais informações sobre este tópico, bem como os links para outras ferramentas e recursos úteis que o SkyCiv pode oferecer.
Como usar a calculadora de momento de inércia SkyCiv
Assista ao vídeo de demonstração abaixo para começar a usar nossa calculadora.
Basta escolher a forma da seção transversal que deseja avaliar na lista suspensa, insira as dimensões da seção escolhida e clique em Calcular.
Esta calculadora multifuncional gratuita foi obtida de nosso software de análise estrutural completo. Isso permite que você:
- Calcule o momento de inércia (I) de uma seção de viga (Momento de inércia de área)
- Calcule o centroide ou baricentro (C) nos eixos X e Y de uma seção de viga
- Calcule o primeiro momento da área (Momento de inércia estático) (Q) de uma seção de viga
- Calcule o Módulo de Seção (Z) de uma seção de viga
- Calcule a constante de torção (J) de uma seção de viga
Definições de propriedades da seção
A calculadora do momento de inércia irá calcular com precisão uma série de propriedades de seção importantes usadas em engenharia estrutural. Aqui está uma lista concisa dos termos e definições de propriedade de seção:
- Área da Seção (A) – A área da seção é um cálculo bastante simples, mas usado diretamente em cálculos de esforços (quanto mais área de seção transversal, quanto mais força axial)
- Momento de inércia (Iz, Iy) – também conhecido como segundo momento de área, é um cálculo usado para determinar a resistência de um membro e sua resistência à deflexão. Quanto maior este número, quanto mais forte a seção é. Existem dois eixos aqui:
- Eixo principal (Iz) – Isso é sobre o eixo Z e normalmente é considerado o eixo principal, pois geralmente é a direção mais forte do membro
- Eixo menor (Iy) - Isso é sobre o eixo Y e é considerado o eixo menor ou mais fraco. Isso ocorre porque as seções não são projetadas para exigir tanta força sobre este eixo
- Também é importante notar que se uma forma tem as mesmas dimensões em ambas as direções (quadrado, circular etc.) esses valores serão iguais em ambas as direções. Veja Momento de Ineria de um círculo para saber mais.
- o centro de gravidade (Cz, Cy) – este é o centro de massa para a seção e geralmente tem um componente Z e Y. Para formas simétricas, este será o centro geométrico. Para formas não simétricas (como seções angulares, o canal) estes estarão em locais diferentes. Aprenda a calcular o centróide de uma seção de viga. A calculadora acima também funciona como uma calculadora de centróide, calculando o centróide X e Y de qualquer tipo de forma.
- Momento de inércia estático (Qz, Qy) – Também conhecido como Primeiro Momento da Área, isso mede a distribuição da área de uma seção de viga de um eixo. Como o momento de inércia, estes estão na direção Z e Y. Estes são normalmente usados em cálculos de tensão de cisalhamento, portanto, quanto maior for este valor, mais forte é a seção contra cisalhamento. A calculadora fornecerá este valor, mas clique aqui para saber mais sobre como calcular o primeiro momento de área.
- Módulo de seção elástica (Sz, Sy na América. Zz, Zy na Grã-Bretanha ou Austrália) – Também conhecidos como módulos de seção estáticos, e são usados em cálculos de esforços de flexão. Eles geralmente são calculados para a seção considerando as fibras superior e inferior. Por exemplo, Szt é o módulo de seção sobre o eixo Z para a fibra superior da seção.
- Constante de Torção (J) - também conhecido como o momento polar de inércia ou J, é um valor que descreve a resistência de um material à torção ou deformação torcional.
- O módulo de seção de plástico (S) - uma medida da capacidade de uma forma de seção transversal para resistir à flexão plástica, usado para estimar a tensão de um material quando ele começa a ceder (e atinge seu limite plástico) sob uma carga específica e é normalmente usado para o projeto e análise de vigas sob cargas.
Outros parâmetros - Estes são resultados mais avançados calculados pelo SkyCiv Section Builder completo:
- Produto da Inércia (sobre os eixos Z e Y): Uma medida da resistência de uma forma à rotação em torno de um eixo específico, igual ao produto vetorial da distância do eixo a qualquer ponto na forma e o componente correspondente do momento de inércia do ponto.
- Módulo de seção de plástico (sobre os eixos Z e Y): Uma medida da capacidade de uma forma de seção transversal para resistir à flexão plástica, usado para estimar a tensão de um material quando ele começa a ceder (e atinge seu limite plástico) sob uma carga específica.
- Eixo neutro plástico (sobre os eixos Z e Y): Um eixo em uma forma de seção transversal através do qual todas as forças que atuam na forma devem passar para resultar em deformação plástica.
- Área de cisalhamento (sobre os eixos Z e Y): A área de uma forma de seção transversal que é eficaz em resistir a forças de cisalhamento.
- Distância do centro de cisalhamento ao centróide (em ambos os eixos Z e Y): A calculadora de centróide SkyCiv ajuda a calcular a distância entre o centro de cisalhamento e o centróide de uma forma de seção transversal.
- Constante de Torção (Usando FEA): Um valor que descreve a resistência de um material à torção ou deformação por torção, calculado usando a Análise de Elementos Finitos.
- Raio de torção: A distância de um eixo na qual a área de uma forma de seção transversal deve ser concentrada para resultar na mesma constante de torção que a forma real.
- Constante de empenamento: Um valor que descreve a resistência de um material à deformação ou distorção.
- Constante de Monossimetria (sobre os eixos Z e Y): Uma medida de quão simétrica uma forma de seção transversal é sobre um eixo específico, com um valor de zero indicando simetria perfeita.
- Raio de Giro (sobre os eixos Z e Y): A distância de um eixo em que a área de uma forma de seção transversal deve ser concentrada para resultar no mesmo momento de inércia que a forma real.
- Ângulo de rotação do eixo principal: O ângulo entre o eixo neutro e o eixo principal de uma forma de seção transversal.
Sobre o momento de inércia, centróides e outras propriedades de seção
Também compilamos mais informações para calcular o momento de inércia das seções. Este tutorial deve ajudar a fornecer uma base de conhecimento completo relacionado ao momento de inércia, centróides, módulo da seção e outras propriedades geométricas importantes da seção. Nos segmentos abaixo, incluímos o que é momento de inércia, como calcular o centróide, momento de inércia e equações MOI comuns com a ajuda do SkyCiv Moment of Inertia and Centroid Calculator.
O que é Momento de Inércia?
O Momento de Inércia (mais tecnicamente conhecido como o momento de inércia da área, ou segundo momento de área) é uma importante propriedade geométrica usada na engenharia estrutural. Está diretamente relacionado à quantidade de resistência do material que sua seção possui..
De um modo geral, Uma análise detalhada, mais força sua seção tem, e, consequentemente, menos ele irá defletir sob carga. O momento de inércia de um retângulo, Uma análise detalhada, é tecnicamente uma medida de quanto torque é necessário para acelerar a massa em torno de um eixo - daí a palavra inércia em seu nome.
Como encontrar o momento de inércia - Retangular
Para calcular o momento de inércia de um retângulo, você pode usar a fórmula:
I = (b * h^3) / 12
I é o momento de inércia do retângulo
b é a largura do retângulo
h é a altura do retângulo
É importante notar que a unidade de medida para b e h deve ser consistente (por exemplo., polegadas, milímetros, etc.). Além disso, a unidade do resultado final depende da unidade de entrada, por exemplo, se a entrada for em metros, a unidade do resultado seria m^4.
Exemplo de Cálculo do Momento de Inércia
Digamos que temos um retângulo com as seguintes dimensões:
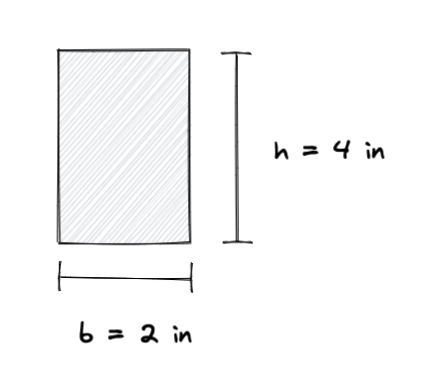
Usando a fórmula do momento de inércia, podemos calcular o momento de inércia do retângulo da seguinte forma:
I = (b * h^3) / 12
I = (2 * 4^ 3) / 12
I = (2 * 64) / 12
= 10.67 em^4
Então o momento de inércia do retângulo é 10.67 polegada^4. Este momento de inércia é sobre o eixo centroidal, lembre-se de que se você precisar encontrar o momento de inércia em relação a um eixo diferente, você precisará usar uma fórmula diferente ou realizar uma transformação. Você também pode verificar se a unidade é sempre o produto da potência da unidade de entrada, neste caso, todas as unidades de entrada são polegadas, então o resultado está em polegadas^4.
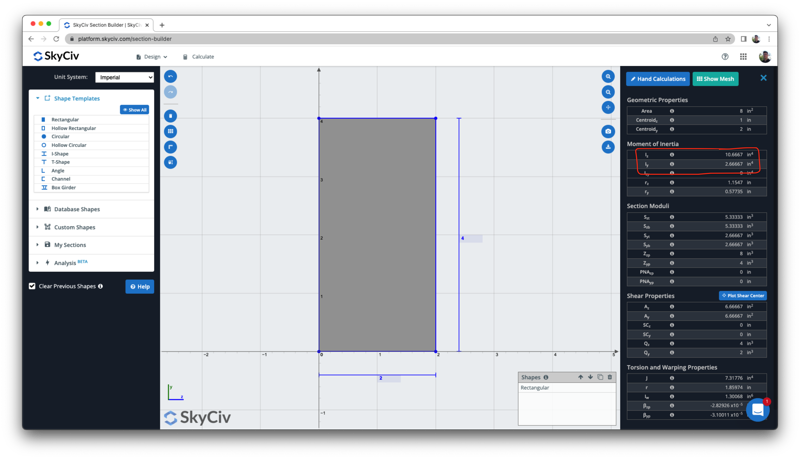
Podemos verificar este resultado com a calculadora de momento livre de inércia acima, que mostra o mesmo resultado de 10.6667 em^4:
Como encontrar o momento de inércia - Viga I
Agora vamos ver um caso mais complexo onde a seção transversal é uma viga I, com diferentes dimensões de mesa. O conceito é o mesmo, no entanto, a abordagem neste caso é bem diferente. Basicamente, precisamos olhar para a viga I como uma combinação de diferentes retângulos e somar as diferentes partes para obter as seções Momento de inércia completo. Resumidamente, precisamos seguir estes três passos:
- Calcule o eixo neutro para toda a seção
- Calcule o momento de inercia de cada peça
- Calcule o momento de inércia usando o Teorema dos Eixos Paralelos - que é essencialmente a soma do momento individual de inércias
Então, vamos considerar a seguinte seção:
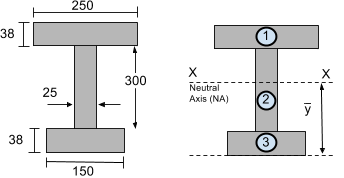
O Eixo Neutro (EN) está localizado no centróide. Esta é essencialmente uma média ponderada da área e distância do fundo para cada segmento. Nós simplesmente precisamos usar a equação do centróide para calcular a vertical (sim) centróide de uma forma multissegmentada.

Pegaremos o datum ou linha de referência da parte inferior da seção da viga. Agora vamos encontrar Ai e yi para cada segmento da seção da viga em I mostrada acima, de modo que o centroide vertical ou centroide y possa ser encontrado.


Agora temos o centróide. Podemos continuar a calcular o momento de inércia. Para calcular o momento de inércia total da seção, precisamos usar o "Teorema do Eixo Paralelo" conforme definido abaixo:

Uma vez que o dividimos em três partes retangulares, devemos calcular o momento de inércia de cada uma dessas seções. Agora podemos usar a fórmula simplificada do momento de inércia retangular:
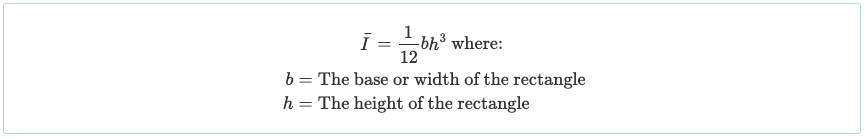
Agora temos todas as informações de que precisamos para usar o "Teorema do Eixo Paralelo" e encontre o momento de inércia total da seção da viga I. Em nosso exemplo de momento de inércia:

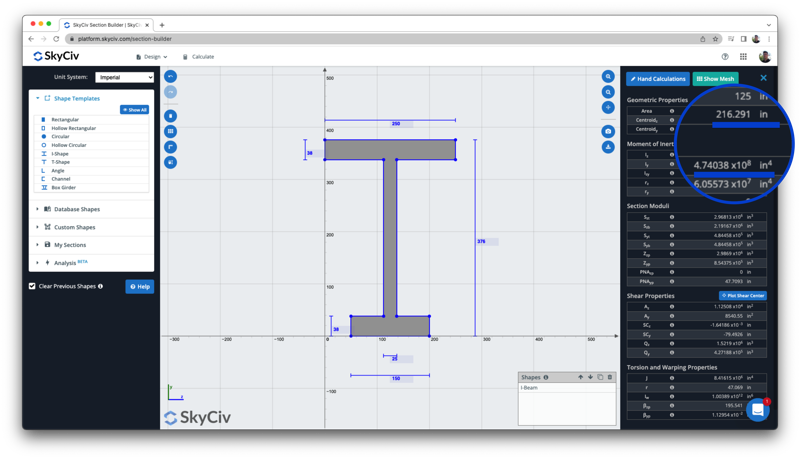
De novo, podemos comparar este resultado com o da calculadora de inércia de momento livre para comparar os resultados do centróide e do momento de inércia, onde tanto o centróide (216.29 no) e momento de inércia (4.74 x 10^8 em^4) coincidem:
Equações do Momento de Inércia
Equações simples também podem ser usadas para calcular o momento de inércia de formas e seções comuns. Estas são equações rápidas de momento de inércia que fornecem valores rápidos e são uma ótima maneira de fazer referências cruzadas ou verificar novamente seus resultados. Concentrando-se apenas em formas simples, o diagrama abaixo mostra algumas dessas equações:
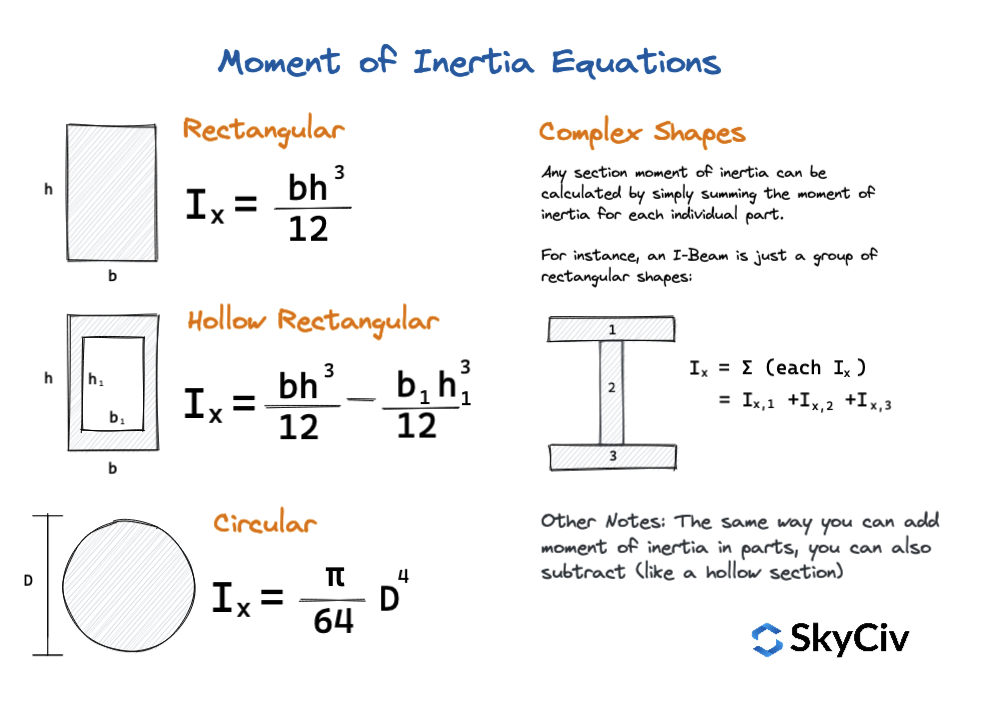
Calculadora de centroides SkyCiv
Um centróide, também conhecido como o 'centro geométrico', é o centro de massa de um objeto com densidade uniforme. Uma demonstração simplificada de um centróide, seria o local em que você precisaria colocar um lápis para equilibrá-lo em seu dedo. O local em que o lápis está equilibrado e não cai do seu dedo seria o local aproximado do centróide do lápis. Ele considera a massa e a densidade do material para determinar o ponto em que a massa do lápis é igual nos dois lados do seu dedo, e, portanto, representa o 'centro de massa' do lápis.
A Calculadora de centroide SkyCiv usa FEA para fornecer resultados altamente precisos em segundos, não importa quão complexa seja a forma. Na versão premium, os usuários podem inserir as coordenadas dos pontos que definem a forma e nossa calculadora fornecerá as coordenadas do centróide. Isso inclui a capacidade de criar formas personalizadas por meio da importação de DXF, múltiplo (composto) de seções e de seções definidas por pontos personalizados.
Além de sua velocidade e precisão, nossa calculadora de centroides também é incrivelmente fácil de usar. Com uma interface de usuário simples, você pode inserir as dimensões de sua seção e calcular as propriedades da seção (incluindo o centróide da seção da viga) em segundos. Esteja você trabalhando em um projeto de dimensionamento, experimentando diferentes seções ou estudando para um exame, a Calculadora de centroides SkyCiv é a ferramenta perfeita para ajudá-lo a fazer o trabalho.
Calculadora de Módulo de Seção
Como observado anteriormente, esta ferramenta gratuita também fornece um cálculo do módulo de seção elástica, no entanto, se você está começando como engenheiro, pode não entender o que é o Módulo de seção. Simplificando, o módulo de seção é uma propriedade de seção de uma seção transversal que mede a resistência à flexão e é calculada como a razão entre o momento de inércia e a distância do eixo neutro à fibra mais distante. O módulo de seção elástica é representado nesta equação como simplesmente:
Onde,
- S é o módulo de seção
- I é o momento de inércia da seção em relação ao eixo neutro
- y é a distância do eixo neutro ao ponto mais distante da seção
Existem dois tipos de Módulo de Seção: Elástico e Plástico. Na América, S é normalmente usado para se referir ao Módulo de Seção Elástica, enquanto Z é usado para se referir ao Módulo de Seção Plástica. Na Grã-Bretanha e na Austrália, estes são normalmente invertidos. Módulo de seção elástica é normalmente referido com uma letra Z, enquanto o módulo de seção de plástico é referido com uma letra S.
No geral, o módulo de seção elástica é usado para projeto de seção porque é aplicável até o ponto de escoamento para a maioria dos metais. Metais normalmente não são projetados para ir além do ponto de escoamento do material.
Documentação Adicional
Consulte as páginas de documentação a seguir para obter informações mais detalhadas sobre o momento de inércia, como calculá-los para várias formas, e como usar nossa calculadora centróide:
Mais ferramentas gratuitas disponíveis
SkyCiv também oferece outras ferramentas, como ferramenta de dimensionamento de vigas I e o software de projeto estrutural gratuito. Também se mostra uma representação gráfica de sua seção de viga. Então, se você quiser calcular o momento de inércia do círculo, momento de inércia de um retângulo ou qualquer outra forma, sinta-se à vontade para usar o software abaixo ou nosso SkyCiv Section Builder completo.
A SkyCiv oferece uma ampla gama de softwares de Análise e Projeto Estrutural em Nuvem para engenheiros. Como uma empresa de tecnologia em constante evolução, estamos comprometidos com a inovação e o desafio dos fluxos de trabalho existentes para economizar tempo dos engenheiros em seus processos de trabalho e projetos.
Precisa de mais funcionalidades?
Atualize para uma versão plano profissional para desbloquear os recursos completos