Como calcular o momento de inércia de uma seção de viga (Momento de inércia de área)
Antes de encontrarmos o momento de inércia de uma seção de viga (também conhecido como segundo momento de área de uma seção de viga), seu centróide (ou centro de massa) deve ser conhecido. Por exemplo, se o momento de inércia da seção sobre sua horizontal (XX) eixo foi necessário, em seguida, o vertical (sim) o centróide seria necessário primeiro (Por favor, veja nossos tutoriais em calcular o centroide de uma seção de viga e calculando o momento estático/primeiro da área).
Antes de começarmos, se você estivesse procurando por nosso Calculadora de momento de inércia grátis por favor clique no link para saber mais. Isso irá calcular o centróide, momento de inércia, e outros resultados e até mostrar os cálculos passo a passo! Mas para agora, vamos ver um guia passo a passo e um exemplo de como calcular o momento de inércia:
Etapa 1: Segmente a seção da viga em partes
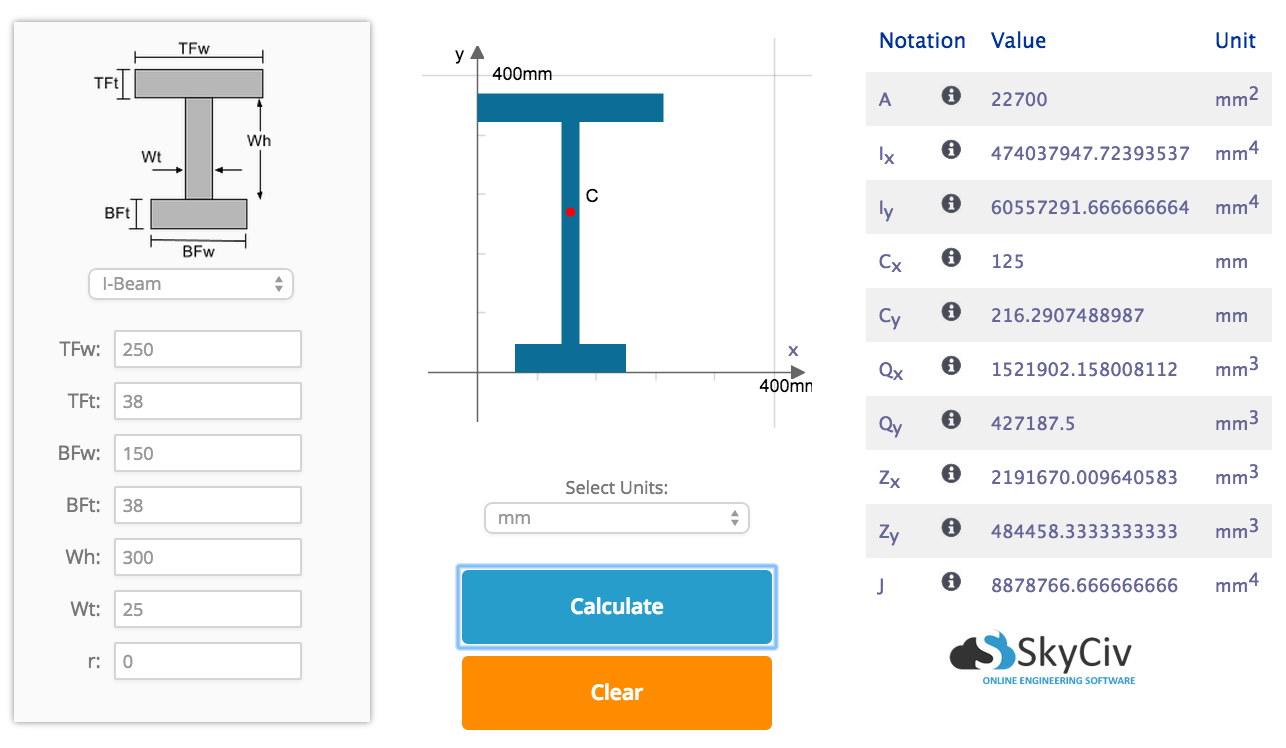
Ao calcular o momento de inércia da área, devemos calcular o momento de inércia de segmentos menores. Tente dividi-los em seções retangulares simples. Por exemplo, considere a seção da viga I abaixo, que também foi apresentado em nosso tutorial de centroide. Decidimos dividir esta seção em 3 segmentos retangulares:
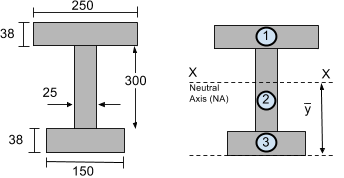
Etapa 2: Calcule o eixo neutro (EN)
O Eixo Neutro (EN) ou o eixo horizontal XX está localizado no centroide ou centro de massa. Em nosso tutorial de centroide, o centróide desta seção foi anteriormente considerado 216.29 mm da parte inferior da seção – isso é abordado em nosso como encontrar o centroide de uma forma tutorial. Estes também podem ser simplesmente calculados a partir do nosso calculadora centróide ou de comum equações do centroide.
Calculando o centroide, ou Eixo Neutro, é essencial em como calcular o momento de inércia de uma viga, pois este é o eixo no qual o momento de inércia atua.
Etapa 3: Calcule o momento de inércia
Para calcular o momento de inércia total da seção, precisamos usar o “Teorema do Eixo Paralelo”:

Uma vez que o dividimos em três partes retangulares, devemos calcular o momento de inércia de cada uma dessas seções. É amplamente conhecido que a equação do momento de inércia de um retângulo em torno de seu eixo centróide é simplesmente:
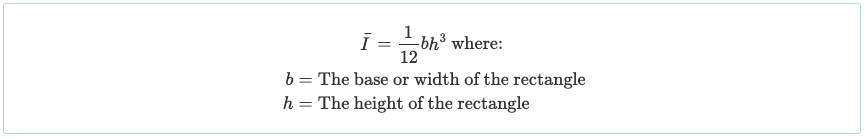
O momento de inércia de outras formas é frequentemente declarado na capa / verso dos livros ou neste guia do momento de formas de inércia. No entanto, a forma retangular é muito comum para seções de viga, então provavelmente vale a pena memorizar.
Agora temos todas as informações de que precisamos para usar o “Teorema do Eixo Paralelo” e encontre o momento de inércia total da seção da viga I. Em nosso exemplo de momento de inércia:

Então, você tem nosso guia sobre o cálculo da área de momento para seções de viga. Este resultado é crítico na engenharia estrutural e é um fator importante na deflexão de uma viga. Esperamos que você tenha gostado do tutorial e aguardamos seus comentários..
Calculadora de momento de inércia grátis
Existem muitas maneiras de calcular o momento de inércia, uma delas é usar software para facilitar o processo. Como uma nota rodapé: Às vezes, isso é incorretamente definido como segundo momento de inércia, porém isso está incorreto. Os dois nomes para esses resultados são: momento de inércia, ou segundo momento da área.
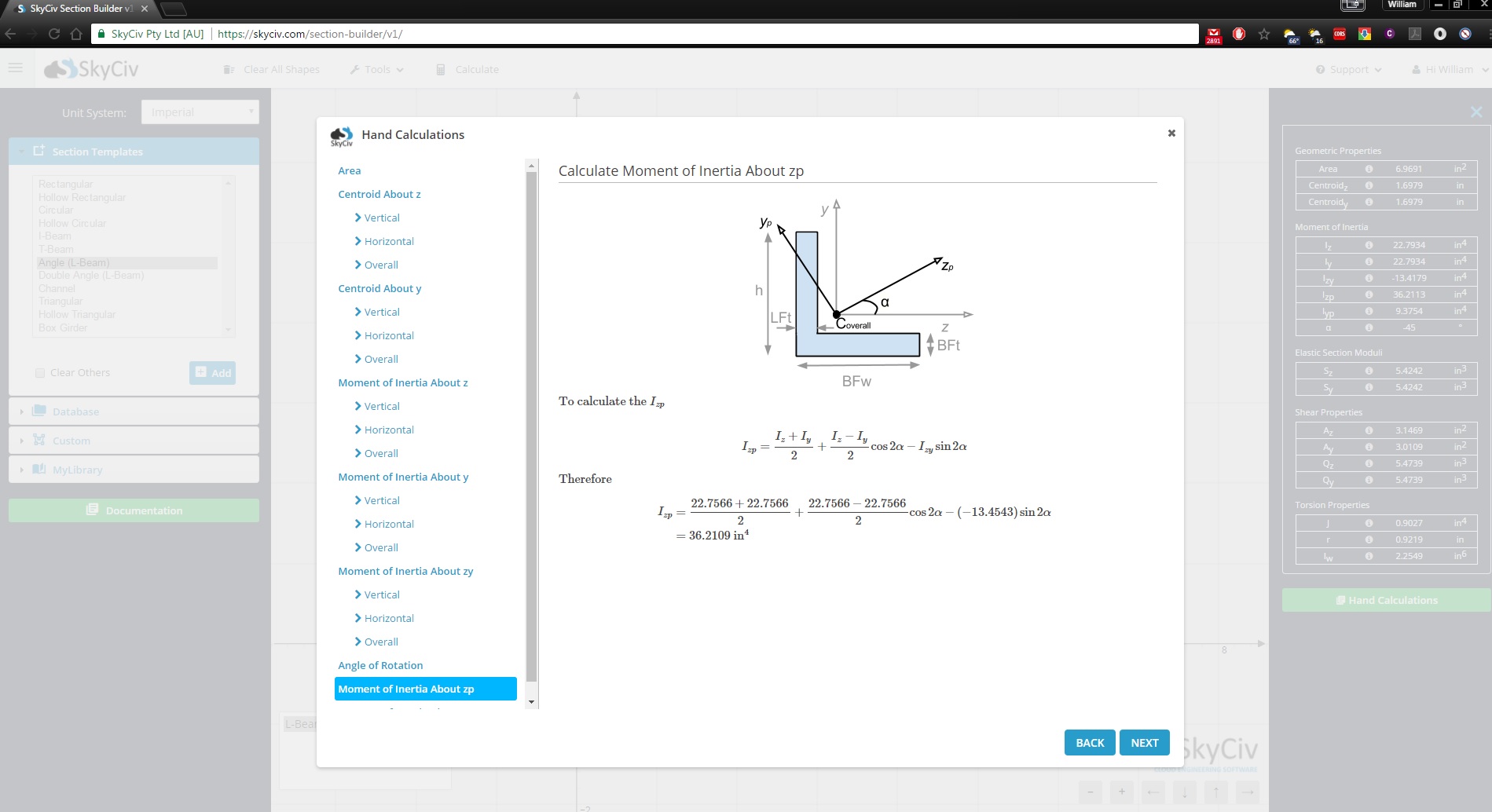
SkyCiv Section Builder fornece cálculos completos do momento de inércia. Este módulo interativo irá mostrar-lhe os cálculos passo a passo de como encontrar o momento de inércia: