Cálculo do centróide: Um guia simples sobre como calcular o centroide
O centróide ou centro de massa das seções da viga é útil para análise de vigas quando o momento de inércia é necessário para cálculos como cisalhamento/tensão de flexão e deflexões. Este artigo orienta você através de um processo simples de como calcular o centroide e apresenta a Calculadora Free Centroid SkyCiv.
Como encontrar o centroide
Em primeiro lugar, você precisa saber como encontrar o centróide. As seções de viga são geralmente compostas de uma ou mais formas. Então, para encontrar o centroide de uma área de seção de feixe inteira, primeiro precisa ser dividido em segmentos apropriados. Depois disto, a área e o centróide de cada segmento individual precisam ser considerados para encontrar o centróide de toda a seção.
Como calcular o centróide (Equação Centroide):
Considere a seção da viga I mostrada abaixo. Para calcular o centróide vertical (na direção y) pode ser dividido em 3 segmentos conforme a seguinte figura:
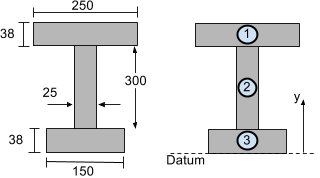
Agora, basta usar a equação do centroide para calcular a vertical (Y) centróide de uma forma multissegmentada:

Vamos pegar o datum ou linha de referência da parte inferior da seção do feixe. Agora vamos encontrar umI com sua distancia YI para cada segmento da seção da viga I mostrada acima, de modo que o centróide vertical ou y possa ser encontrado.
[math]
\texto{Segmento 1:}\\
\começar{alinhar}
{A}_{1} &= 250 times38 = 9500 {\texto{ milímetros}}^{2}\\
{Y}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \texto{ milímetros}\\\\
\fim{alinhar}
[math]
[math]
\texto{Segmento 2:}\\
\começar{alinhar}
{A}_{2} &= 300 times25 = 7500 {\texto{ milímetros}}^{2}\\
{Y}_{2} &= 38 + \tfrac{300}{2} = 188 \texto{ milímetros}\\\\
\fim{alinhar}
[math]
[math]
\texto{Segmento 3:}\\
\começar{alinhar}
{A}_{3} &= 38 times150 = 5700 {\texto{ milímetros}}^{2}\\
{Y}_{3} &= tfrac{38}{2} = 19 texto{ milímetros}\\\\
\fim{alinhar}
[math]

No caso de a seção transversal ser composta por dois materiais ou um material compósito, então, um dos materiais terá que ser multiplicado pela razão modular de modo que toda a seção da equação se torne uniforme.
[math]
n = frac{E_{1}}{E_{2}}
[math]
Normalmente, E1 é o módulo de elasticidade do material não predominante, e E2 é o módulo de elasticidade do material predominante, embora qualquer ordem que seja preferida não afete a solução do centroide. Ajustando para o segundo material, a equação do centroide se torna a seguinte.
[math]
\bar{Y}= frac{\soma{A}_{I}{Y}_{I}+\soma {n}{A}_{I}{Y}_{I}}{\soma{A}_{I}+\soma {n}{A}_{I}}
[math]
Calcule o centróide do feixe com SkyCiv
Calcular o centróide do feixe é importante, mas calculá-los manualmente pode ser demorado. SkyCiv oferece um Calculadora Centroide Gratuita que automatiza esse processo para você, ajudando você a encontrar a vertical (Y) e horizontal (x) centróides de seções de feixe com facilidade e precisão!
Esta ferramenta é uma versão gratuita do SkyCiv Section Builder, um software abrangente de análise de seção on-line para analisar geometrias, a curvatura, propriedades de seção de cisalhamento e torção, bem como FEA e projeto de concreto armado. Com esta ferramenta, você pode criar seções personalizadas usando modelos predefinidos ou definir suas próprias formas com pontos, linhas, ou importações DXF de CAD.
Para explorar todas as funcionalidades SkyCiv Section Builder e experimente a facilidade de modelar e analisar sua seção, Cadastre-se gratuitamente hoje!
Visite a próxima etapa: Calculando o momento estático.

