No projeto de conexão de aço, parafusos geralmente são projetados como um grupo de parafusos que atuará como um corpo para resistir a uma determinada carga. A resistência de um grupo de parafusos é geralmente calculada pela força de controle de seu parafuso mais crítico.. As cargas diretas são distribuídas entre o número total de parafusos, enquanto o momento induzido devido à excentricidade das cargas é distribuído em relação ao momento de inércia do grupo de parafusos e à distância do centróide. Essa análise é chamada de análise elástica. Devido às suas suposições simplificadas e conservadoras sobre a distribuição de carga, muitas vezes produz conexões aparafusadas superdimensionadas.
Ao falar sobre engenharia de valor e projetos econômicos, a abordagem inelástica é preferida pela maioria dos fabricantes. Requer um número menor de parafusos para a mesma magnitude de cargas. Para fazer a abordagem inelástica, o centro de rotação instantâneo (ICOR) método usando iterações é a melhor maneira.
Neste artigo, vamos demonstrar como calcular a força de um conexão parafusada usando o método ICOR. As reações por parafuso serão calculadas usando a Equação (7-1) nas páginas 7-7 do Manual AISC 15ª Edição. Isso será usado para verificar se a localização assumida do centro instantâneo do grupo de parafusos está correta. Finalmente, assim que tivermos a localização correta do IC, vamos então calcular o coeficiente do grupo de parafusos C para determinar sua resistência.
O uso do método ICOR para obter o coeficiente do grupo de parafusos é um processo longo, pois requer um método de tentativa e erro para obter o Centro Instantâneo (CI) localização. Hoje em dia, com o uso de solucionadores de computador, o IC de um grupo de parafusos pode ser facilmente calculado usando iterações programadas. SkyCiv Bolt Group Solver usa um método de iteração rápida para determinar a localização do IC e o coeficiente do grupo de parafusos em apenas alguns segundos. Atualmente está implementado no AS 4100 código de design, mas será integrado ao restante dos códigos de design em breve.
Obtendo as propriedades do grupo Bolt
Vamos começar nossa análise simples em um grupo de parafusos de quatro parafusos carregados com uma carga de cisalhamento vertical excêntrica de 10 kips. A excentricidade da carga ao longo do eixo x é 4 polegadas à direita do grupo de parafusos. O ângulo da vertical é zero e a excentricidade ao longo do eixo y é zero.
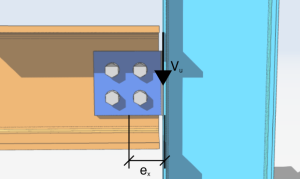
\(V_{você} = 10kips \)
\(\teta = 0 graus)
\(e_{x} = 4 dentro)
\(e_{sim} = 0in)
A primeira coisa a fazer é obter as coordenadas de todos os parafusos em nosso grupo de parafusos. O uso de guias visuais e tabelas é altamente recomendado.
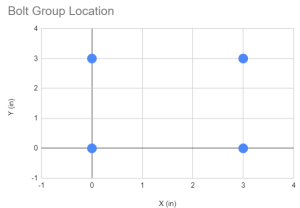
| Código da loja | X (no) | Y (no) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Para obter o centróide do grupo de parafusos ao longo do x- e eixos y, precisamos da formula abaixo.
Deixar \(n \) = número total de parafusos
\(X_{CG} = frac{\soma X}{n}\)
\(Y_{CG} = frac{\soma Y}{n} \)
Então, nossa solução é:
\(X_{CG} = frac{\soma X}{n} = frac{0 no + 0 no + 3 no + 3 no}{4} = 1.5 dentro)
\(Y_{CG} = frac{\soma Y}{n} = frac{0 no + 3 no + 0 no + 3 no}{4} = 1.5 dentro)
Assuma a localização do I.C.
Depois de obter o centroide, assumiremos a localização do centro instantâneo \(CI). Como primeira tentativa, podemos assumir que o IC está localizado no centroide geométrico do grupo de parafusos.
Então, presumir
\(X_{CI} = X_{CG} = 1.5 dentro)
\(Y_{CI} = Y_{CG} = 1.5 dentro)
Então, tabulamos o deslocamento de cada parafuso para a localização do IC. Podemos simplesmente fazer isso obtendo a distância ao longo de x e a distância ao longo de y primeiro, então pegue seu deslocamento
| Código da loja | cx (no) | cy (no) | c (no) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Onde,
\(c_{x} = X_{I} – X_{CI}\)
\(c_{sim} = Y_{I} – Y_{CI}\)
\(c = sqrt{{\deixou(c_{x} \direito)}^{2} + {\deixou(c_{sim} \direito)}^{2}}\)
Para Parafuso Não. 1, nossa solução é
\(c_{x} = 0 pol – 1.5 em = -1.5 dentro)
\(c_{sim} = 0 pol – 1.5 em = -1.5 dentro)
\(c = sqrt{{\deixou( -1.5 à direita)}^{2} + {\deixou( -1.5 à direita)}^{2}} = 2.121in\)
Calcule a deformação por parafuso wrt distância de IC
Consequentemente, depois de obter as distâncias dos parafusos da localização do IC assumida, calculamos então a deformação de cada parafuso em função de sua distância.
A deformação máxima por parafuso, definido como \(\Delta_{max} = 0.34 dentro), é baseado em dados experimentais para um parafuso ASTM conforme descrito na página AISC 7-8. Usando proporção linear, e configuração \(\Delta_{max} = 0.34 dentro), podemos calcular a deformação de um parafuso individual em relação à sua porção até a distância máxima \(c_{max}\). A equação para obter é mostrado abaixo.
\(\Delta_{1} = 0,34in vezes esquerda( \fratura{c}{c_{max}}\direito) \)
Para Parafuso Não. 1, a deformação é
\(\Delta_{1} = 0,34in vezes esquerda( \fratura{2.121 no}{2.121 no}\direito)\)
Para o resto dos parafusos, as deformações calculadas são tabuladas abaixo.
| Código da loja | \(\Delta\) (no) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Obtenha as reações por parafuso
Uma vez que temos a deformação por parafuso, podemos então usar AISC 15th Ed. Eq (7-1) para obter as reações por parafuso.
\(R = R_{ult} \deixou ( 1 – e ^{-10\Delta}\direito )^{0.55}\)
A \(R_{ult}\) na equação é a carga última assumida em um parafuso, que podemos definir como a resistência ao cisalhamento do parafuso.
\(R_{ult} = phi R_{n} \)
Para nosso exemplo, usaremos uma resistência ao cisalhamento do parafuso de \(24.4 kip). Também é permitido usar outro valor, pois isso será cancelado quando calcularmos o coeficiente do grupo de parafusos \(C) mais tarde.
Para Parafuso Não. 1, a reação calculada é
\(R = R_{ult} \deixou ( 1 – e ^{-10\Delta}\direito )^{0.55}\)
\(R = 24.4 kip esquerda ( 1 – e ^{-10 \times left ( 0.34 à direita )}\direito )^{0.55}\)
\(R = 23.949 kip)
Para o resto dos parafusos, as reações calculadas são as seguintes. Ao mesmo tempo, os componentes da reação do parafuso \(R ) ao longo de x e y também são mostrados.
| Código da loja | R (kip) | Detalhes e parâmetros do modelo (kip) | Ry (kip) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
Para Parafuso Nº 1, as soluções para obter os componentes x e y são mostradas abaixo.
\(R_{x} = -R esquerda ( \fratura{c_{sim}}{c} \direito ) = -23.949 \times left ( \fratura{-1.5no}{2.121no} \direito ) = 23.949 kip)
\(R_{sim} = R esquerda ( \fratura{c_{x}}{c} \direito ) = 23.949 \times left ( \fratura{1.5no}{2.121no} \direito ) = 23.949 kip)
além disso, devemos obter a carga de momento induzida por parafuso devido à excentricidade. Para calcular isso, usamos os componentes \(R_{x}\) e \(R_{sim}\) e multiplicá-los com as excentricidades \(c_{sim}\) e \(c_{x}\), respectivamente.
Para Parafuso Nº 1, o momento em que a reação ao IC é
\(M_{r} = -R_{x}c_{sim} + -R_{sim}c_{x} \)
\(M_{r} = -16.937 kip vezes esquerda ( -1.5à direita) + -16.937 kip vezes esquerda ( -1.5 à direita ) \)
\(M_{r} = 50.811 galinha em)
Para o resto dos parafusos, as reações de momento correspondentes são tabuladas abaixo.
| Código da loja | Senhor (frango em) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀Sr = 101.622 |
Verificando a localização do IC
Agora que temos as reações de cisalhamento e momento por parafuso, vamos usar isso para determinar a quantidade de carga de Pu que este grupo de parafusos resiste. Para fazer isso, obteremos a resultante da soma de todas as reações ao longo de x e a soma de todas as reações ao longo de y.
Da seção anterior, nós calculamos isso
\(\soma R_{x}=0kip\)
e
\(\soma R_{sim}=0kip\)
Então,
\(a pressão exercida na parede segue uma distribuição vertical uniforme{você} = sqrt{{\deixou( \soma R_{x} \direito)}^{2} + {\deixou( \soma R_{sim} \direito)}^{2}} = 0 kip)
Uma vez que a carga resultante \(a pressão exercida na parede segue uma distribuição vertical uniforme{você} = 0kip), podemos decidir neste momento não prosseguir com a verificação, pois nossos dados serão apenas zero. Também podemos inferir que a primeira localização assumida de I.C., que está no centroide do grupo de parafusos, está incorreto. Contudo, para esta discussão, vamos prosseguir com os passos abaixo.
\(a pressão exercida na parede segue uma distribuição vertical uniforme{ux} = -P_{você}pecadoesquerda ( \teta certo ) = 0 kip \)
\(a pressão exercida na parede segue uma distribuição vertical uniforme{uy} = -P_{você}cosesquerda ( \teta certo ) = 0 kip \)
\(M_{você} = -P_{ux}\deixou ( Y_{CG} + e_{sim} – Y_{CI} \direito ) + -a pressão exercida na parede segue uma distribuição vertical uniforme{uy} \deixou (X_{CG} + e_{x} – X_{CI} \direito ) = 0 kip \)
Desde a,
\(a pressão exercida na parede segue uma distribuição vertical uniforme{ux} \neq soma R_{x} \)
\(a pressão exercida na parede segue uma distribuição vertical uniforme{uy} \neq soma R_{sim} \)
\(M_{você} \eu não sou M_{r} \)
Portanto, a localização assumida de I.C. está incorreto. Agora podemos prosseguir com a próxima localização assumida.
O SkyCiv tem integração total do cálculo do grupo de parafusos no Módulo Padrão Australiano. Quer experimentar nosso software de design de conexão?
Segunda Iteração
Para nossa segunda iteração, Suponhamos que o I.C.. está localizado nas coordenadas abaixo.
Presumir
\(X_{CI} = 0.062 dentro)
\(Y_{CI} = 1.5 dentro)
Então, vamos fazer as etapas que fizemos em nossa primeira iteração. Resumindo, a tabela abaixo mostrará as coordenadas, a distância de cada parafuso do I.C assumido, e a deformação correspondente em relação à distância.
| Código da loja | X (no) | Y (no) | cx (no) | cy (no) | c (no) | \(\Delta\) (no) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Observe que o centroide calculado do grupo de parafusos ainda é o mesmo, pois nada mudou nas coordenadas do parafuso.
\(X_{CG} = 1.5 dentro)
\(Y_{CG} = 1.5 dentro)
Então, calculamos as reações ao longo de x, reações ao longo de y, e o momento correspondente. Os valores estão tabulados abaixo.
| Código da loja | R (kip) | Detalhes e parâmetros do modelo (kip) | Ry (kip) | Senhor (frango em) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀Sr = 222 |
A continuação, determinamos a carga resultante de todas as reações ao longo de x e y.
\(a pressão exercida na parede segue uma distribuição vertical uniforme{você} = sqrt{{\deixou( \soma R_{x} \direito)}^{2} + {\deixou( \soma R_{sim} \direito)}^{2}}\)
\(a pressão exercida na parede segue uma distribuição vertical uniforme{você} = sqrt{{\deixou( 0 kipright)}^{2} + {\deixou( 40.703 kipright)}^{2}}\)
\(a pressão exercida na parede segue uma distribuição vertical uniforme{você} = 40.703 kip)
Então, os componentes da carga resultante com base no dado \(\theta\) é mostrado abaixo.
\(a pressão exercida na parede segue uma distribuição vertical uniforme{ux} = -P_{você}pecado esquerda ( \teta certo ) = -41kip times sin left ( 0 grau direito )= 0 kip)
\(a pressão exercida na parede segue uma distribuição vertical uniforme{uy} = -P_{você}cos esquerda ( \teta certo ) = -41kip vezes cos esquerda ( 0 grau direito )= -41 kip)
Em seguida, usaremos esses componentes para resolver a carga de momento sobre o I.C assumido.
\(M_{você} = -P_{ux} \deixou ( Y_{CG} + e_{sim} – Y_{CI} \direito) + a pressão exercida na parede segue uma distribuição vertical uniforme{uy} \deixou ( X_{CG} + e_{x} – X_{CI} \direito)\)
\(M_{você} = -0 kip esquerda ( 1.5 no +0 no – 1.5 à direita) + 41 kip esquerda ( 1.5 no +4 no – 0.06 à direita)\)
\(M_{você} = -222 galinha em)
A continuação, vamos comparar o calculado Pux, Pux, e Mvocê às reações do grupo de parafusos.
\(a pressão exercida na parede segue uma distribuição vertical uniforme{ux} \Aproximadamente – \soma R_{x}\)
\(a pressão exercida na parede segue uma distribuição vertical uniforme{uy} \Aproximadamente – \soma R_{sim}\)
\(M_{você} \Aproximadamente – \soma M_{você}\)
Como o lado esquerdo é quase igual ao lado direito da equação, podemos dizer que a localização assumida de I.C. está correto!
Resolvendo para o coeficiente C
Uma vez que o I. C.. a localização é determinada, agora podemos obter o coeficiente do grupo de parafusos C com a fórmula abaixo.
\(C = frac{a pressão exercida na parede segue uma distribuição vertical uniforme{você}}{\phi R_{n}} = \frac{40.703 kip}{24.4 kip} = 1.668\)
Calculadora Gratuita de Grupo de Parafusos
Verifique como projetamos nossas conexões aparafusadas com esta abordagem usando nosso Calculadora gratuita de projeto de conexão de aço! Para mais funcionalidade, inscreva-se em nosso software 3D estrutural hoje para começar!

