Neste artigo, desenvolveremos um exemplo de projeto de laje usando a última versão do ACI-318-19: “Requisitos de Código para Concreto Estrutural,” consistindo na modelagem em SkyCiv de um edifício baixo de concreto armado com foco na comparação de resultados de software e cálculos manuais por um método aceito pela ACI: “O Método de Projeto Direto para Lajes.” Este procedimento consiste em atribuir em diferentes faixas ao longo das principais direções e pórticos do edifício o momento total por fatores convenientes para determinar a quantidade de armadura e a localização na laje.

Esperamos que você tenha lido o artigo anterior, Projeto de placas em S3D, apresentar-se à modelagem e design de placas usando o SkyCiv. Outra informação útil que sugerimos que você considere é encontrada em Como modelar placas? Depois de concluir a leitura de ambos os documentos, sinta-se à vontade para mergulhar no seguinte exemplo de comparação de laje completa!

Disposição geral do edifício

As imagens a seguir mostram uma vista isométrica e as dimensões do plano do exemplo a ser calculado. O edifício possui duas lajes planas elevadas sem vigas entre os apoios dos pilares.

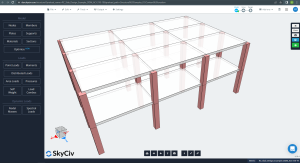
Figura 1. Vista isométrica do exemplo de construção

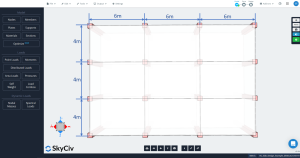
Figura 2. Dimensões do plano de laje

Método de projeto direto para lajes bidirecionais (DDM)

Limitações

ACI 318 permite usar o DDM para projetar lajes de concreto armado para cargas de gravidade, que reúnem alguns requisitos de acordo com a geometria, relações de carga, simetria, etc. Podemos resumir essas limitações na lista a seguir (Notas PCA):

• “Deve haver três ou mais vãos contínuos em cada direção.”: Figura 2 mostra três vãos em cada direção principal, longitudinal e transversal. OK!
• “Os painéis de laje devem ser retangulares com uma proporção de vão maior para menor (linha central a linha central de suportes) não superior a 2.”: De acordo com a figura 2, a proporção é igual a \({\fratura{l_1}{4}= frac{6m}{4m}=1,5 < 2}\). OK!
• “Comprimentos de vão sucessivos (linha central a linha central de suportes) em cada direção não deve diferir em mais de 1/3 do maior vão”. Comprimentos de vão são os mesmos em cada direção, 6m para longitudinal e 4m para transversal. OK!
• “As colunas não devem ser deslocadas mais de 10% do intervalo (na direção do deslocamento) de qualquer eixo entre as linhas centrais de colunas sucessivas”. O exemplo de construção não tem deslocamentos nas colunas. OK!
• “As cargas devem ser uniformemente distribuídas, com a carga ativa não fatorada ou de serviço não mais que duas vezes a carga morta não fatorada ou de serviço (L/D ≤ 2)”. Tomando os valores de cada carga de gravidade, a razão é definida como \({\fratura{L}{D}= frac{2}{7.8}=0,256 < 2}\). OK!.
• “Para lajes apoiadas por vigas de duas vias, a rigidez relativa das vigas em duas direções perpendiculares deve satisfazer os requisitos mínimos e máximos indicados no código.” Já satisfeito; não há vigas nas lajes. OK!
• “A redistribuição de momentos negativos por código não é permitida.” Pela simplicidade do exemplo, não será necessário redistribuir os momentos negativos nas lajes. OK!.

Definição de faixas longitudinais e transversais

A laje em DDM deve ser dividida em duas faixas principais para a análise e projeto de uma malha de linha específica: coluna e tiras do meio. A largura para tiras de coluna é o menor de \({\fratura {l_1}{4}}\) e \({\fratura{l_2}{4}}\), Onde \({l_1}\) é o comprimento do vão ao longo da grade de linha e \({l_2}\) é o comprimento transversal perpendicular.

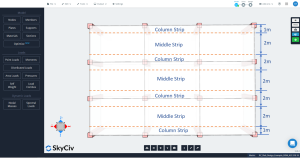
Figura 3. Coluna longitudinal e tiras intermediárias.

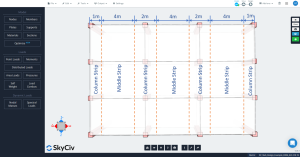
Figura 4. Coluna transversal e tiras intermediárias.

Espessura mínima

ACI-318 sugere o uso da equação: \({t_{min}}= {\fratura{l_n}{30}}={\fratura{6m-0.50m}{30}}=0,1833m = 0,20m)

Verificação preliminar da resistência ao cisalhamento

Antes de calcular a armadura do vergalhão de aço, recomenda-se verificar a capacidade de cisalhamento da laje, um para cisalhamento direto na ligação e outro para capacidade de punção no pilar da laje de ligação.

Para calcular a demanda de cisalhamento, usamos as seguintes cargas de gravidade:

• Laje de peso próprio: \({SW ={\gama_c}\vezes {t_{laje}}={24 {\fratura{kN}{m^3}}}\vezes {0.20m}=4,8{\fratura{kN}{m^2}} }\)
• Carga morta sobreposta: \({SD={3 {\fratura{kN}{m^2}}}}\)
• Carga morta total (SW+SD): \({D={7.8 {\fratura{kN}{m^2}}}}\)
• Carga viva (Ocupação residencial) : \({L={2 {\fratura{kN}{m^2}}}}\)
• Carga de força fatorada (1.2D+1,6L): \({q_{você}={12.56 {\fratura{kN}{m^2}}}}\)

A primeira verificação de cisalhamento é a “cisalhamento” na guia de entrada à esquerda, onde a imagem a seguir indica a área a ser considerada para obtenção do cisalhamento total. Nós inspecionamos cada direção, tomando a área mais extensa.

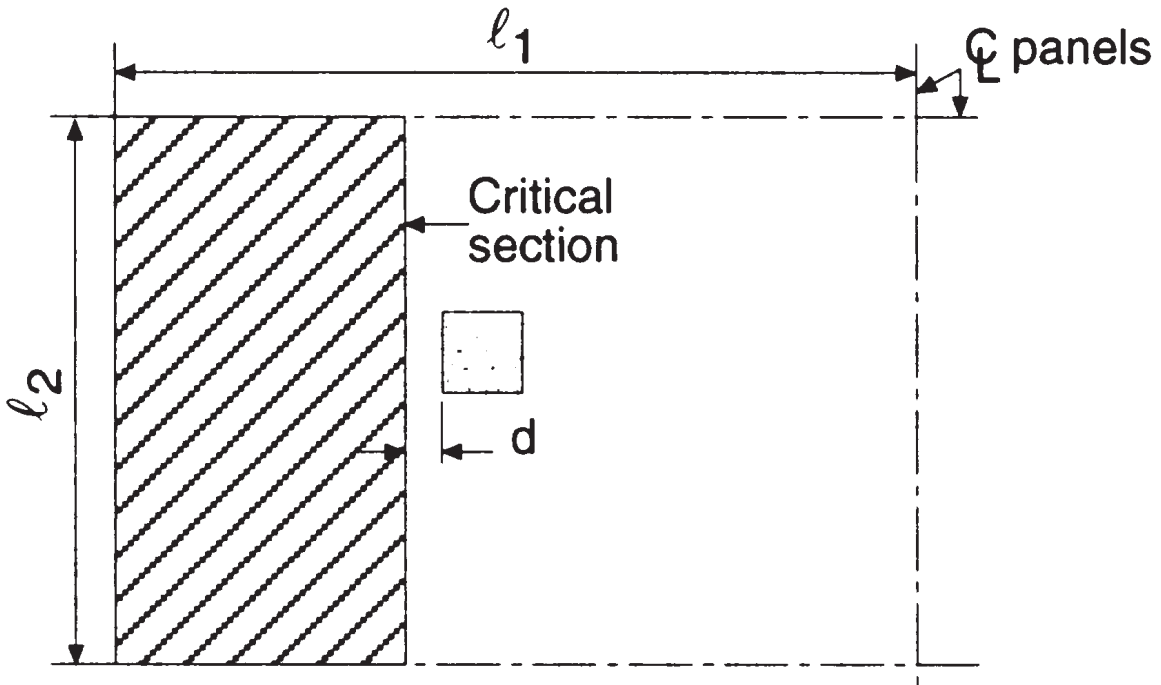
Figura 5. Cisalhamento da viga na coluna interna (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

Onde:

• Comprimento do vão na direção longitudinal, \({l_1 = 6,0m }\)
• Comprimento do vão na direção transversal, \({l_2 = 4,0m}\)
• Área tributária total, cisalhamento na direção longitudinal \({A_t = l_2 vezes (\fratura{l_1}{2}-\fratura{c_1}{2}-d) = 4,0m vezes (\fratura{6.0m}{2}-\fratura{0.50m}{2}-0.17m) = 10.32 m^2}\) (selecionado)
• Área tributária total, cisalhamento na direção transversal, \({A_t = l_1 vezes (\fratura{l_2}{2}-\fratura{c_2}{2}-d) = 6,0m vezes (\fratura{4.0m}{2}-\fratura{0.50m}{2}-0.17m) = 9.48 m^2}\)
• Dimensão de colunas quadradas, \({c_1 = c_2 = 0,50m}\)
• Distância d, \({d = h_{laje} – cobertura = 0,20m – 0.03m = 0,17m }\)

Portanto, o cisalhamento máximo da viga na coluna interior é

\({V_u =q_uvezes A_t =12,56 {\fratura{kN}{m^2}}\vezes 10.32 m^2 = 129.62 kN }\)

Isso vai ser comparado com a resistência ao cisalhamento, \({\phi_sV_c}\)

• Resistência do concreto, \({f'_c = 25 MPa}\)
• Rendimento da resistência do aço do vergalhão, \({f_y = 420 MPa}\)
• \({\fi_s = 0.75}\)
• \({\phi_sV_c = 0,17phi_s lambda sqrt(f’_c) b_w d; b_w=l_2}\)

\({\phi_sV_c = 0,17vezes 0,75vezes 1vezes sqrt(25 MPa) \vezes 4000 mmvezes 170 mm = 433.50 kN }\)

Podemos ver que a resistência ao cisalhamento é maior que a demanda de cisalhamento: \({\phi_sV_c = 433.50 kN > V_u = 129.62 kN }\) OK!.

De acordo com as imagens a seguir, temos que calcular a capacidade de punção e a força a ser resistida pelo concreto na ligação interior laje-pilar. A intenção do código ao verificar o punçoamento é manter baixos valores de tensão de cisalhamento.

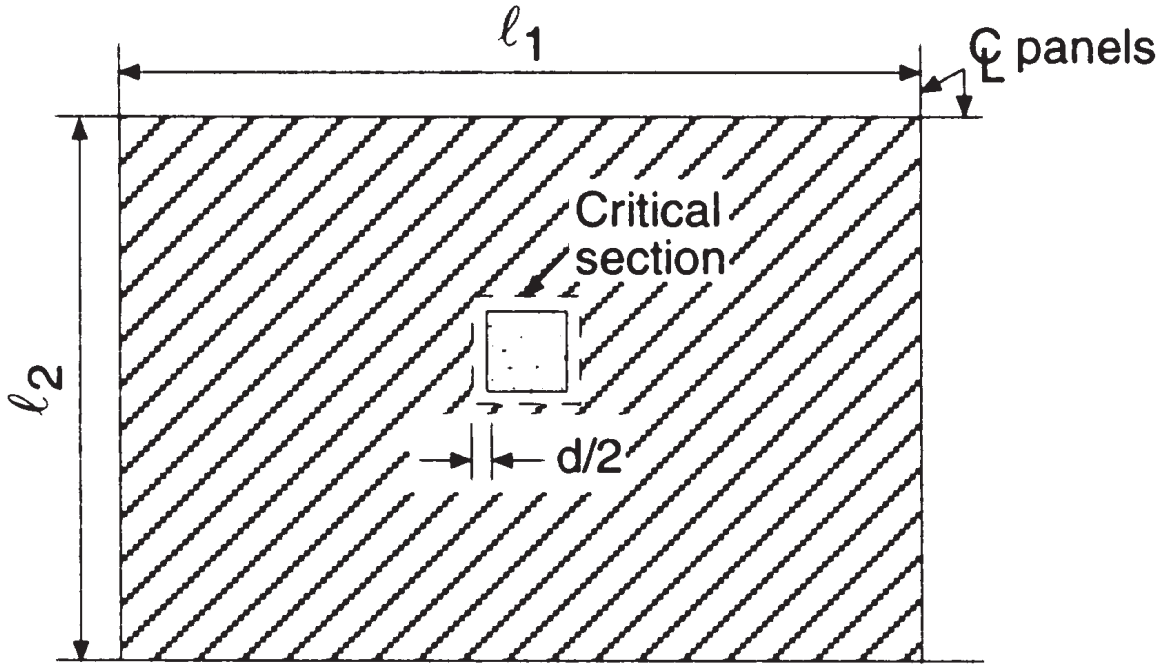
Figura 6. Cisalhamento bidirecional na coluna interior (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

• Área tributária total, punção, \({A_t = l_1 vezes l_2 – (c_1+d)^2 = 6,0m vezes 4,0m – (0.50m+0,17m)A partir da elevação do solo gerada a partir das elevações do Google 23.55 m^2}\) (mesma área para ambas as direções principais)

A força de cisalhamento total a ser resistida é

\({V_u =q_uvezes A_t =12,56 {\fratura{kN}{m^2}}\vezes 23.55 m^2 = 295.79 kN }\)

Para obter a capacidade de punção em uma laje de duas direções, usaremos o método empírico estabelecido pelo código ACI-318, que considera a tensão de cisalhamento máxima disponível no perímetro efetivo na seção crítica. A expressão mais conservadora para a coluna interna é

• Capacidade de punção, \({\phi_sV_c = 0,33phi_s lambda sqrt(f’_c) b_0 d; b_0=4vezes (c_1+d)}\)

Portanto, temos a resistência ao cisalhamento de

\({\phi_sV_c = 0,33vezes 0.75 \vezes 1 \sqrt(25 MPa) \vezes (4\vezes (500 mm+170 mm)\vezes 170mm) = 563.81 kN }\)

Podemos ver que a resistência ao cisalhamento é maior que a demanda de cisalhamento: \({\phi_sV_c = 563.81 kN > V_u = 295.75 kN }\) OK!.

Verificamos as demandas de cisalhamento unidirecional e bidirecional na ligação interna do pilar. Devido a ambas as demandas serem menores que suas respectivas capacidades ou resistências, passaremos agora a calcular a armadura principal do vergalhão para a flexão da laje.

Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!

Inscreva-se no SkyCiv!

Momento estático fatorado total por vão.

O momento máximo que pode ser desenvolvido em uma viga dupla de extremidade fixa é um momento isostático igual a \({M=frac{wvezes {l_1}^ 2}{8}}\) (Veja a figura 6).

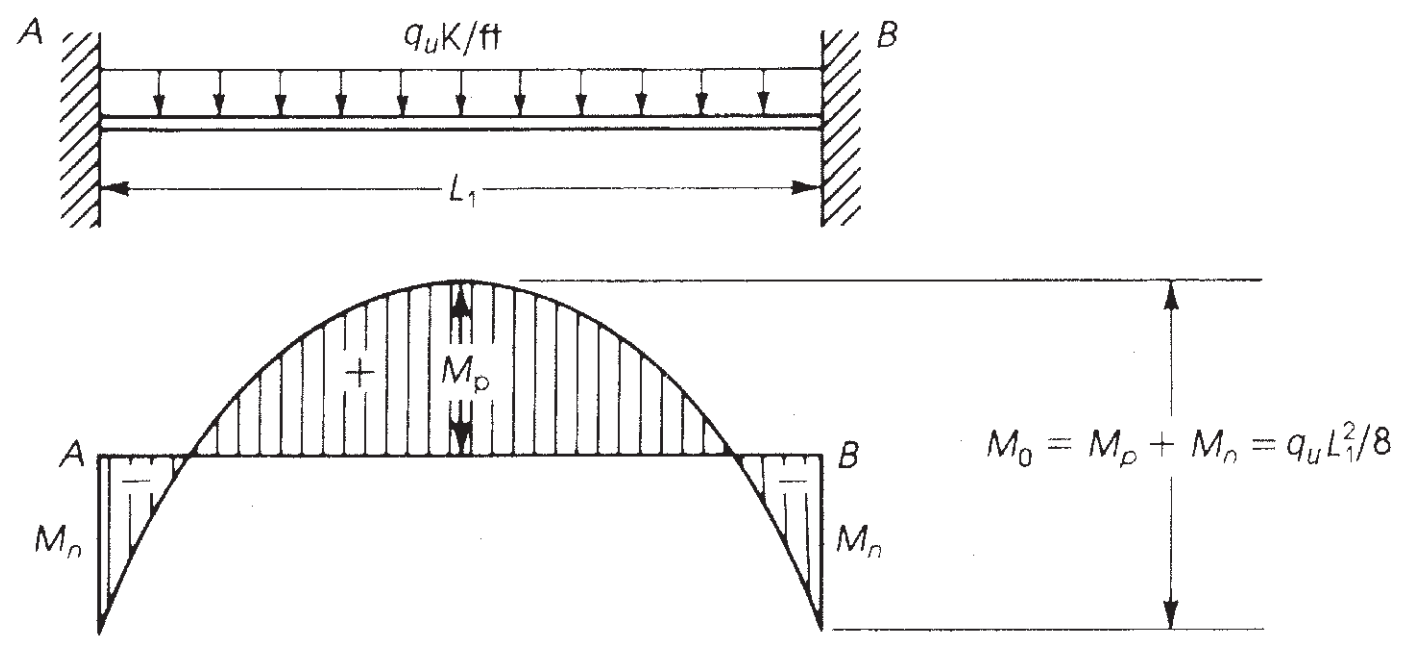
Figura 7. Momento fletor em uma viga de extremidade fixa. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

A ACI-18 adota esse princípio e, para o Método de Design Direto (DDM), estabelece o momento estático máximo a ser considerado por vão \({M_0}\)

Direção longitudinal:

• \({M_0 = frac {q_uvezes l_2vezes {eu_{n,1}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\fratura{kN}{m^2}}\vezes 4,0mvezes (6m-0.50m)^ 2}{8}=189,97 kN-m}\)

Direção transversal:

• \({M_0 = frac {q_uvezes l_1vezes {eu_{n,2}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\fratura{kN}{m^2}}\vezes 6,0mvezes (4m-0.50m)^ 2}{8}=115,40 kN-m}\)

O próximo passo é atribuir este momento total considerando o tipo de painel, interior ou exterior. (Veja a figura 7). Depois disso, devido aos vãos serem contínuos, é necessário dividir também o momento em positivo e negativo. Este último é mostrado em imagens 8 e 9.

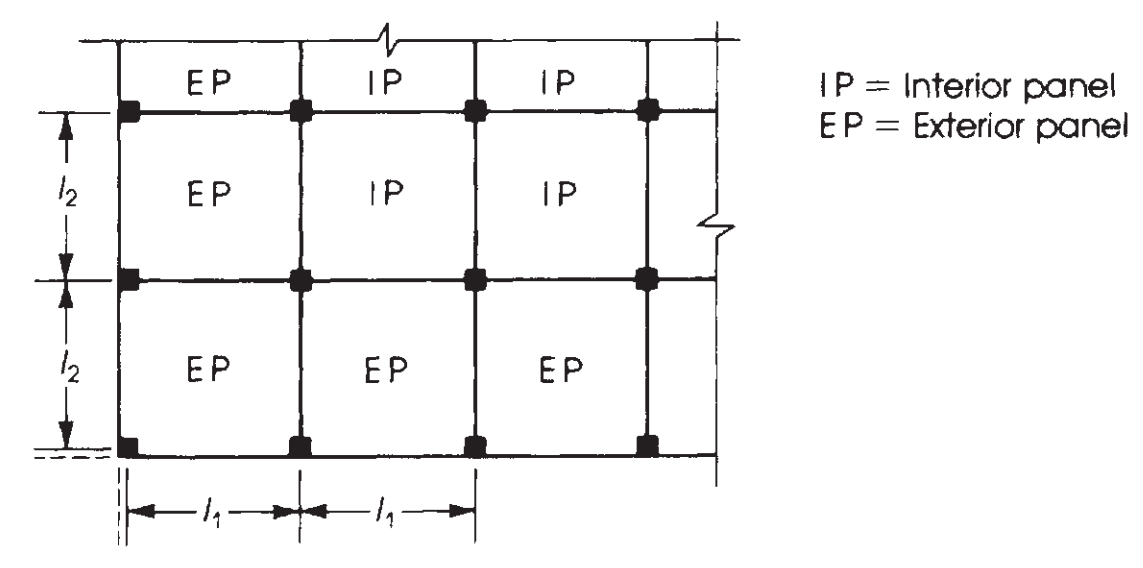
Figura 8. Definição de painéis de acordo com sua posição relativa em um plano de laje. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

 

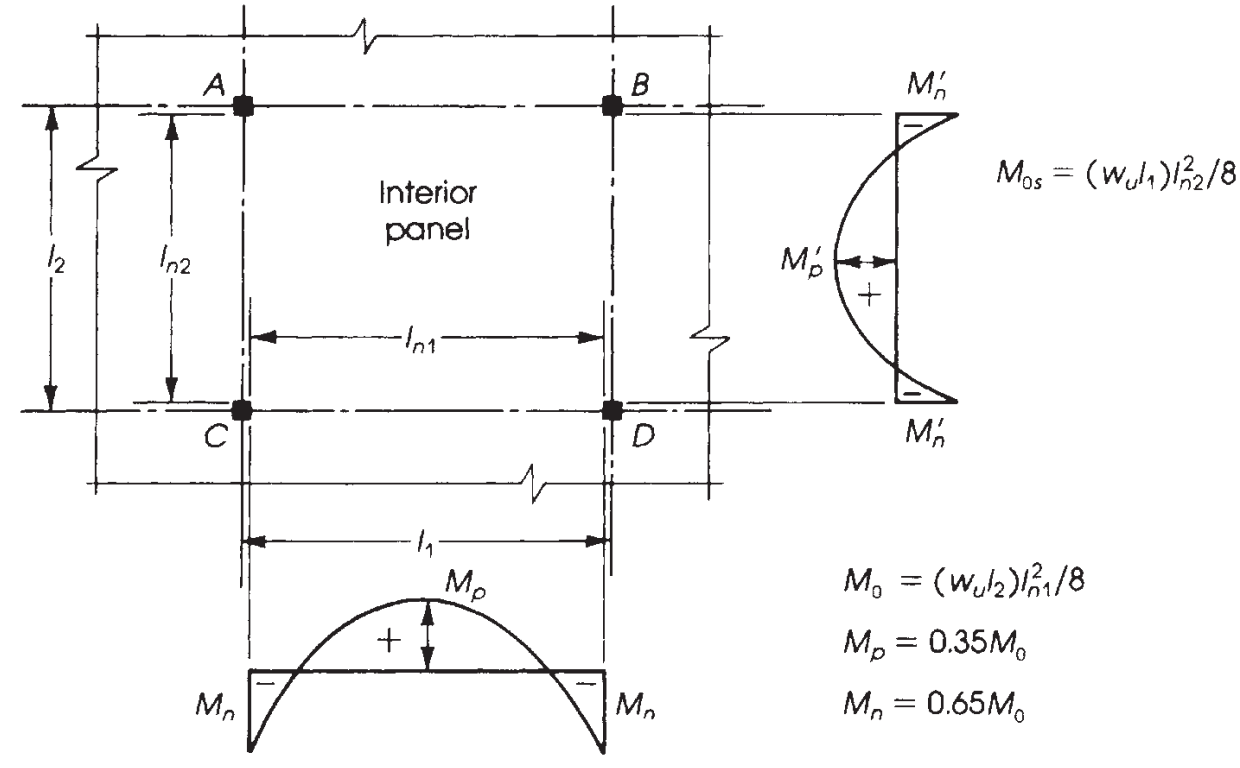
Figura 9. Distribuição de momentos em um painel interior. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

 

É fundamental saber a distribuição correta dos momentos dependendo da laje que estamos projetando. Neste exemplo, temos o último caso na imagem a seguir (figura 9), “Sem vigas,” aplicado a uma laje plana ou laje maciça sem qualquer viga, nem na borda nem entre suportes.

A principal diferença nos cinco casos mostrados na figura 9 é a fracção de momento a atribuir aos painéis exteriores, em que a restrição relativa no final altera os valores a serem calculados.

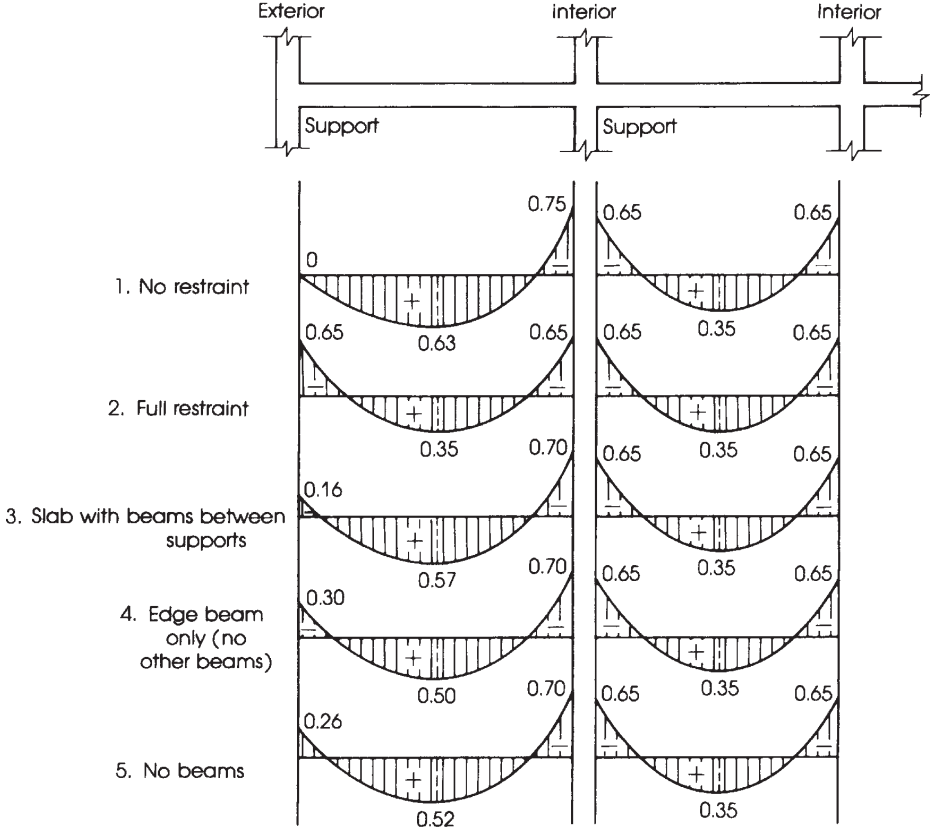
Figura 10. Distribuição do momento estático total em momentos de vão negativos e positivos. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

Distribuição do momento fatorado total \({M_0}\) por vão em momentos negativos e positivos.

Uma vez \({M_0}\) foi calculado, é hora de atribuir a fração de momentos em positivo e negativo em cada faixa de design, enquanto a tensão no aço fs é menor que a tensão de escoamento f, coluna e tiras do meio. Para mais clareza, figura 10 ajuda a especificar o fator apropriado a ser considerado na distribuição do momento total.

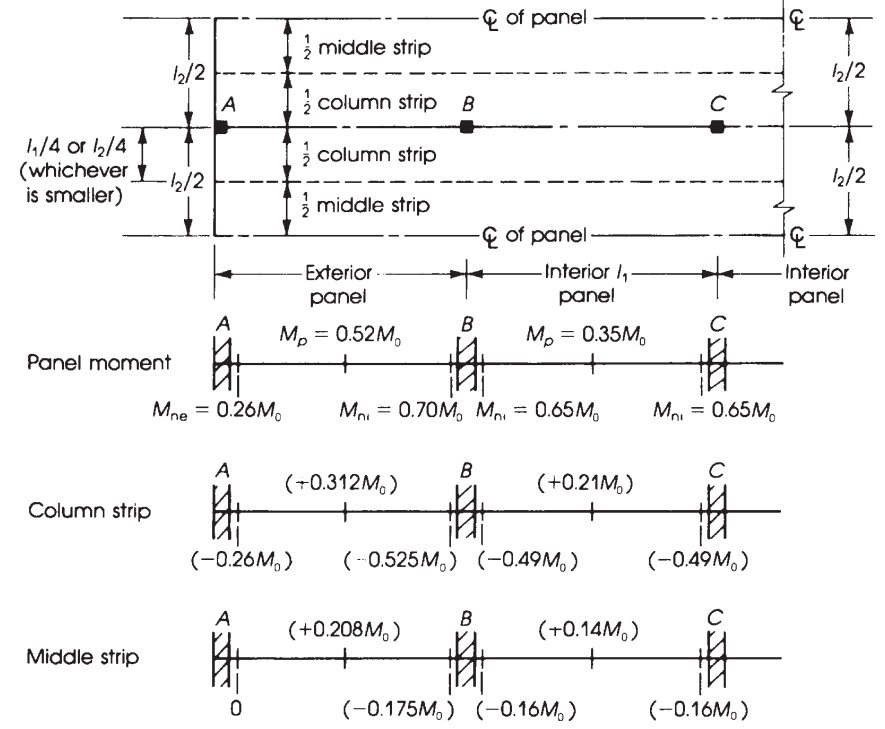
Figura 11. Largura do pórtico rígido equivalente e distribuição de momentos em lajes lisas. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e projeto do concreto estrutural”)

Usando os fatores anteriores indicados na figura 10, obtemos na tabela a seguir o momento último.

Direção longitudinal: \({M_0 = 189.97 kN-m}\)

Período (ES:Exterior, É:Interior)	momento total (kN-m)	Momento de tira de coluna (kN-m)	Momento de tira do meio (kN-m)
Exterior Negativo ES	0.26M0=49,39	0.26M0=49,39	0
ES positivo	0.52M0=98,78	0.31M0=58,89	0.21M0=39,89
ES Negativo Interior	0.70M0=132,98	0.53M0=100,68	0.17M0=32,29
IS positivo	0.35M0=66,49	0.21M0=39,89	0.14M0=26,60
IS negativo	0.65M0=123,48	0.49M0=93,09	0.16M0=30,40

Com o momento uma vez distribuído, é hora de determinar a armadura de aço a ser colocada na laje. Desenvolveremos apenas um cálculo e depois todos os resultados em uma tabela.

Momento no vão externo negativo na tira do pilar, \({M_u = 49.39 kN-m}\)

• Seção controlada por tensão assumida. \({\phi_f = 0.9}\)
• Largura da faixa da coluna, \({b=2,0m}\)
• Área de reforço de aço, \({A_s = frac{M_u}{\phi_fvezes 0,9dvezes fy}= frac{49.39kN-m}{0.9\vezes 0.9(0.17m)\vezes 420 MPa}=853.996 {milímetros}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de reforço de aço, \({UMA_{s,min}=rho_{min}\vezes bvezes d = 0.0018 \vezes 2,0m vezes 0,17m =612 {milímetros}^ 2}\). Agora, verifique se a seção está se comportando como tensão controlada.
• \({a = frac{A_svezes f_y}{0.85\vezes f'cvezes b} = frac{853.996 {milímetros}^2vezes 420 MPa}{0.85\vezes 25 MPavezes 2,0 m }= 8.439 milímetros}\)
• \({c = frac{uma}{\beta_1}= frac{8.439 milímetros}{0.85} = 9,929 mm }\)
• \({\varepsilon_t = (\fratura{0.003}{c})\vezes d – 0.003 = (\fratura{0.003}{9.929milímetros})\vezes 170mm – 0.003 = 0.048 > 0.005 }\) OK!, é uma seção controlada por tensão!.

Período(ES:Exterior, É:Interior)	Momento de Tira de Coluna (kN-m)	\({UMA_{s,calcular} ({milímetros}^ 2)}\)	\({UMA_{s,min} ({milímetros}^ 2)}\)	\({uma (milímetros)}\)	\({c (milímetros)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	49.39	853.996	612.0	8.439	9.929	0.048 > 0.005!
ES positivo	58.89	1018.259	612.0	10.063	11.839	0.040 > 0.005!
ES Negativo Interior	100.68	1740.844	612.0	17.204	20.24	0.022 > 0.005!
IS positivo	39.89	689.733	612.0	6.816	8.019	0.06 > 0.005!
IS negativo	93.09	1609.607	612.0	15.907	18.714	0.024 > 0.005!

Momento no vão externo positivo na faixa intermediária, \({M_u = 39.89 kN-m}\)

• Seção controlada por tensão assumida. \({\phi_f = 0.9}\)
• Largura da faixa intermediária, \({b=2,0m}\)
• Área de reforço de aço, \({A_s = frac{M_u}{\phi_fvezes 0,9dvezes fy}= frac{39.89kN-m}{0.9\vezes 0.9(0.17m)\vezes 420 MPa}=689.733 {milímetros}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de reforço de aço, \({UMA_{s,min}=rho_{min}\vezes bvezes d = 0.0018 \vezes 2,0m vezes 0,17m =612 {milímetros}^ 2}\). Agora, verifique se a seção está se comportando como tensão controlada.
• \({a = frac{A_svezes f_y}{0.85\vezes f'cvezes b} = frac{689.766 {milímetros}^2vezes 420 MPa}{0.85\vezes 25 MPavezes 2,0 m }= 6.816 milímetros}\)
• \({c = frac{uma}{\beta_1}= frac{6.816 milímetros}{0.85} = 8.019 milímetros }\)
• \({\varepsilon_t = (\fratura{0.003}{c})\vezes d – 0.003 = (\fratura{0.003}{8.019milímetros})\vezes 170mm – 0.003 = 0.0605 > 0.005 }\) OK!, é uma seção controlada por tensão!.

Período(ES:Exterior, É:Interior)	Momento de tira do meio (kN-m)	\({UMA_{s,calcular} ({milímetros}^ 2)}\)	\({UMA_{s,min} ({milímetros}^ 2)}\)	\({uma (milímetros)}\)	\({c (milímetros)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	0	0.00	612.0	6.048	7.115	0.069 > 0.005!
ES positivo	39.89	689.733	612.0	6.816	8.019	0.061 > 0.005!
ES Negativo Interior	32.29	558.322	612.0	6.048	7.115	0.069 > 0.005!
IS positivo	26.60	459.937	612.0	6.048	7.115	0.069 > 0.005!
IS negativo	30.40	525.642	612.0	6.048	7.115	0.069 > 0.005!

Direção transversal: \({M_0 = 115.40 kN-m}\)

Período (ES:Exterior, É:Interior)	momento total (kN-m)	Momento de tira de coluna (kN-m)	Momento de tira do meio (kN-m)
Exterior Negativo ES	0.26M0=30,00	0.26M0=30,00	0
ES positivo	0.52M0=60,00	0.31M0=35,77	0.21M0=24,23
ES Negativo Interior	0.70M0=80,78	0.53M0=61,16	0.17M0=19,62
IS positivo	0.35M0=40,39	0.21M0=24,23	0.14M0=16,16
IS negativo	0.65M0=75,01	0.49M0=56,55	0.16M0=18,46

Com o momento uma vez distribuído, é hora de determinar a armadura de aço para colocar na laje. Desenvolveremos apenas um cálculo e depois todos os resultados em uma tabela.

Momento no vão externo negativo na tira do pilar, \({M_u = 30.00 kN-m}\)

• Seção controlada por tensão assumida. \({\phi_f = 0.9}\)
• Largura da faixa da coluna, \({b=2,0m}\)
• Área de reforço de aço, \({A_s = frac{M_u}{\phi_fvezes 0,9dvezes fy}= frac{30.00kN-m}{0.9\vezes 0.9(0.17m)\vezes 420 MPa}=518.726 {milímetros}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de reforço de aço, \({UMA_{s,min}=rho_{min}\vezes bvezes d = 0.0018 \vezes 2,0m vezes 0,17m =612 {milímetros}^ 2}\). Agora, verifique se a seção está se comportando como tensão controlada.
• \({a = frac{A_svezes f_y}{0.85\vezes f'cvezes b} = frac{518.726 {milímetros}^2vezes 420 MPa}{0.85\vezes 25 MPavezes 2,0 m }= 6.048 milímetros}\)
• \({c = frac{uma}{\beta_1}= frac{6.048 milímetros}{0.85} = 7,115 mm }\)
• \({\varepsilon_t = (\fratura{0.003}{c})\vezes d – 0.003 = (\fratura{0.003}{7.115milímetros})\vezes 170mm – 0.003 = 0.069 > 0.005 }\) OK!, é uma seção controlada por tensão!.

Período(ES:Exterior, É:Interior)	Momento de Tira de Coluna (kN-m)	\({UMA_{s,calcular} ({milímetros}^ 2)}\)	\({UMA_{s,min} ({milímetros}^ 2)}\)	\({uma (milímetros)}\)	\({c (milímetros)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	30.00	518.726	612.0	6.048	7.115	0.069 > 0.005!
ES positivo	35.77	618.494	612.0	6.112	7.191	0.068 > 0.005!
ES Negativo Interior	61.16	1057.509	612.0	10.451	12.295	0.038 > 0.005!
IS positivo	24.23	418.958	612.0	6.048	7.115	0.069 > 0.005!
IS negativo	56.55	977.799	612.0	9.663	11.368	0.042 > 0.005!

Momento no vão externo positivo na faixa intermediária, \({M_u = 24.23 kN-m}\)

• Seção controlada por tensão assumida. \({\phi_f = 0.9}\)
• Largura da faixa da coluna, \({b=4,0m}\)
• Área de reforço de aço, \({A_s = frac{M_u}{\phi_fvezes 0,9dvezes fy}= frac{24.23 kN-m}{0.9\vezes 0.9(0.17m)\vezes 420 MPa}=418.958 {milímetros}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de reforço de aço, \({UMA_{s,min}=rho_{min}\vezes bvezes d = 0.0018 \vezes 4,0m vezes 0,17m =1224 {milímetros}^ 2}\). Agora, verifique se a seção está se comportando como tensão controlada.
• \({a = frac{A_svezes f_y}{0.85\vezes f'cvezes b} = frac{1224 {milímetros}^2vezes 420 MPa}{0.85\vezes 25 MPavezes 4,0m }= 6.048 milímetros}\)
• \({c = frac{uma}{\beta_1}= frac{6.048 milímetros}{0.85} = 7.115 milímetros }\)
• \({\varepsilon_t = (\fratura{0.003}{c})\vezes d – 0.003 = (\fratura{0.003}{7.115milímetros})\vezes 170mm – 0.003 = 0.069 > 0.005 }\) OK!, é uma seção controlada por tensão!.

Período(ES:Exterior, É:Interior)	Momento de tira do meio (kN-m)	\({UMA_{s,calcular} ({milímetros}^ 2)}\)	\({UMA_{s,min} ({milímetros}^ 2)}\)	\({uma (milímetros)}\)	\({c (milímetros)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	0.00	0.00	1224.00	6.048	7.115	0.069 > 0.005!
ES positivo	24.23	418.958	1224.00	6.048	7.115	0.069 > 0.005!
ES Negativo Interior	19.62	339.247	1224.00	6.048	7.115	0.069 > 0.005!
IS positivo	16.16	279.420	1224.00	6.048	7.115	0.069 > 0.005!
IS negativo	18.46	319.189	1224.00	6.048	7.115	0.069 > 0.005!

Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!

Inscreva-se no SkyCiv!

Módulo de design SkyCiv S3D

Nesta secção, descrevemos o resultado do projeto usando o módulo para projeto de placas incluído no SkyCiv. Não explicamos como modelar e analisar a estrutura (Para estes, veja artigos relacionados sobre este tópico em nossa documentação: Como modelar uma estrutura no SkyCiv?, Como aplicar cargas no meu modelo de construção? e Como executar uma análise elástica linear?)

É conveniente aplicar uma malha fina às lajes para obter um resultado de projeto preciso. Por favor, dê uma olhada na imagem a seguir para mais clareza.

Figura 12. Malha mais fina aplicada a lajes

O próximo passo é executar o módulo de projeto e selecionar as opções que calculam uma área de vergalhão de aço otimizada.

Figura 13. Definição das propriedades do concreto da laje antes da otimização do projeto.

Figura 14 representa a orientação dos eixos locais da placa. Porque o eixo local 3 é para baixo, a “figura superior” é o fundo, e o “figura inferior” será o topo, assim, tomando corretamente os dados do projeto.

Outro dado importante é o tamanho da malha da laje; é um elemento quadrado de placa com dimensões de planta de 500mm x 500mm. SkyCiv S3D fornece a área de reforço como um valor integrado por elemento finito. Por isso, se quisermos obter a área total do vergalhão de uma coluna ou faixa intermediária, precisamos calcular o valor médio do número de elementos que somam a largura da faixa que está sendo analisada. Por exemplo, para a faixa de coluna, quatro elementos serão considerados (4×0.5m = 2m).

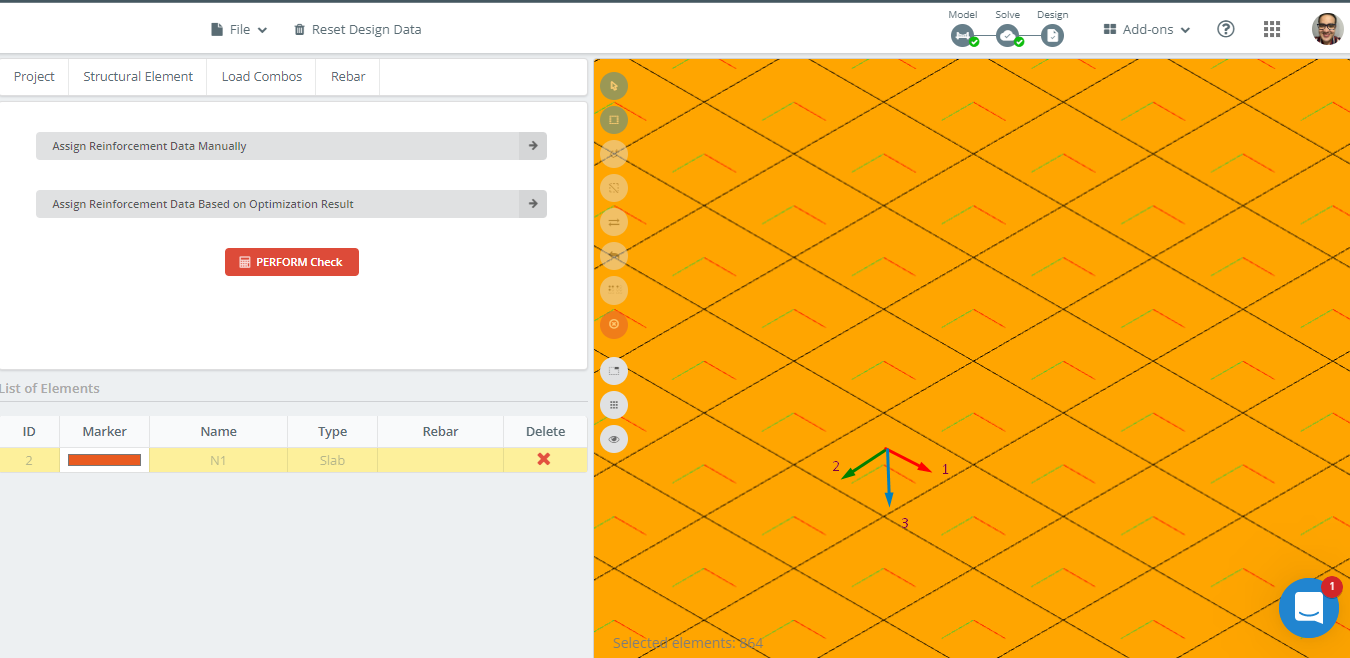
Figura 14. Orientação dos eixos locais no exemplo de laje.

Primeiro, analisamos a área de reforço necessária ao longo da direção longitudinal no eixo 1.

Faixa de coluna

• Momento externo negativo (reforço superior): \({UMA_{s,figura superior} =(119.09\vezes 2 + 952.72 + 833.64 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 1012.27 {milímetros}^ 2}\)
• Momento externo positivo (reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = 4*463.90 \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 927.80 {milímetros}^ 2}\)
• Momento negativo exterior interior (reforço superior): \({UMA_{s,figura superior} =(1071.82\vezes 2 +714.54 \vezes 2 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 1786.36 {milímetros}^ 2}\)
• Momento interior positivo(reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = 4*309.27 \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 618.54 {milímetros}^ 2}\)
• Momento interno negativo (reforço superior): \({UMA_{s,figura superior} =(714.54\vezes 2 +952.73 \vezes 2 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 1667.27 {milímetros}^ 2}\)

faixa do meio

• Momento externo negativo (reforço superior): \({UMA_{s,figura superior} =(119.09\vezes 4)\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 238.18 {milímetros}^ 2}\)
• Momento externo positivo (reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = (463.90\vezes 2 +412.36 \vezes 2 ) \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 876.26 {milímetros}^ 2}\)
• Momento negativo exterior interior (reforço superior): \({UMA_{s,figura superior} =(357.27\vezes 2 +476.36 \vezes 2 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 833.63 {milímetros}^ 2}\)
• Momento interior positivo(reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = 4*257.72 \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 515.44 {milímetros}^ 2}\)
• Momento interno negativo (reforço superior): \({UMA_{s,figura superior} =(357.27\vezes 2 +476.36 \vezes 2 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 833.63 {milímetros}^ 2}\)

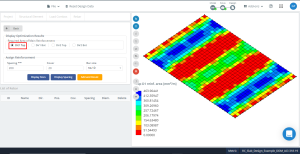
Figura 15. A otimização resulta na direção “1” e o lado de cima (Lado inferior, na realidade).

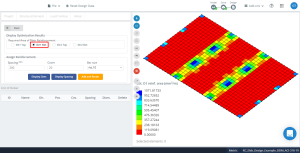
Figura 16. A otimização resulta na direção “1” e o lado de baixo (Lado superior, na realidade).

Finalmente, analisamos a área de reforço necessária ao longo da direção transversal no eixo 2.

Faixa de coluna

• Momento externo negativo (reforço superior): \({UMA_{s,figura superior} =(91.55\vezes 2 + 457.73 + 549.28 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 595.055 {milímetros}^ 2}\)
• Momento externo positivo (reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = (269.68\vezes 3+239.72) \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 524.38 {milímetros}^ 2}\)
• Momento negativo exterior interior (reforço superior): \({UMA_{s,figura superior} =(823.92\vezes 2 +549.28 +457.73)\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 1327.43 {milímetros}^ 2}\)
• Momento interior positivo(reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = (179.79\vezes 3+149.82) \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 344.60 {milímetros}^ 2}\)
• Momento interno negativo (reforço superior): \({UMA_{s,figura superior} =(823.92\vezes 2 +549.28 +457.73)\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 1327.43 {milímetros}^ 2}\)

faixa do meio

• Momento externo negativo (reforço superior): \({UMA_{s,figura superior} =(183.09\vezes 2+91,55vezes 6)\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 457.74 {milímetros}^ 2}\)
• Momento externo positivo (reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = (209.75\vezes 2 +179.79 \vezes 2 +149.82 \vezes 4) \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 689.18{milímetros}^ 2}\)
• Momento negativo exterior interior (reforço superior): \({UMA_{s,figura superior} =(274.64\vezes 2+91,55vezes 6)\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 549.29 {milímetros}^ 2}\)
• Momento interior positivo(reforço inferior): \({UMA_{s,As unidades têm comprimento elevado à potência de} = (119.86\vezes 4 + 89.89\vezes 4) \fratura{{milímetros}^ 2}{m}\vezes 0,50m = 419.50 {milímetros}^ 2}\)
• Momento interno negativo (reforço superior): \({UMA_{s,figura superior} =(274.64\vezes 2+91,55vezes 6 )\fratura{{milímetros}^ 2}{m} \vezes 0,50m = 549.29 {milímetros}^ 2}\)

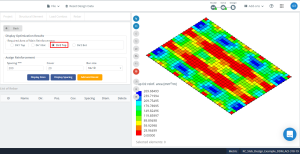
Figura 17. A otimização resulta na direção “2” e o lado de cima (Lado inferior, na realidade).

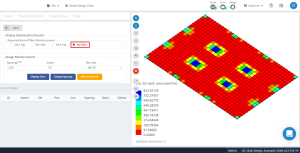
Figura 18. A otimização resulta na direção “2” e o lado de baixo (Lado superior, na realidade).

 

Comparação de resultados

A tabela a seguir mostra os resultados para o DDM (“Método de Design Direto”) e a otimização do vergalhão de aço S3D.

Período (ES:Exterior, É:Interior)	Faixa de coluna (Projeto S3D) \({Como ({milímetros}^ 2)}\)	Faixa de coluna (ACI-318 DDM) \({Como ({milímetros}^ 2)}\)	% Dif	faixa do meio (Projeto S3D) \({Como ({milímetros}^ 2)}\)	faixa do meio (ACI-318 DDM) \({Como ({milímetros}^ 2)}\)	% Dif
Exterior Negativo ES	1012.27	853.996	15.636	238.18	0 (612.0)	100.00
ES positivo	927.80	1018.259	9.75	876.26	689.733	21.287
ES Negativo Interior	1786.36	1740.844	2.48	833.63	558.322 (612.0)	26.586
IS positivo	618.54	689.733	11.51	515.44	459.937 (612.0)	18.734
IS negativo	1667.27	1609.607	3.459	833.63	525.642 (612.0)	26.586

Direção transversal

Período (ES:Exterior, É:Interior)	Faixa de coluna (Projeto S3D) \({Como ({milímetros}^ 2)}\)	Faixa de coluna (ACI-318 DDM) \({Como ({milímetros}^ 2)}\)	% Dif	faixa do meio (Projeto S3D) \({Como ({milímetros}^ 2)}\)	faixa do meio (ACI-318 DDM) \({Como ({milímetros}^ 2)}\)	% Dif
Exterior Negativo ES	595.055	518.726	12.827	457.74	0 (1224)	100.00
ES positivo	524.38	618.494	17.948	689.18	418.958	39.209
ES Negativo Interior	1327.43	1057.509	20.334	549.29	339.247	38.239
IS positivo	344.60	418.958	21.578	419.50	279.42	33.392
IS negativo	1327.43	977.799	26.339	549.29	319.189	41.891

Conclusão

Demonstramos neste artigo que o módulo SkyCiv para projeto de placas calcula a armadura de aço para dobrar a laje de acordo com o código ACI-318-19. Comparando os resultados da análise nas tiras de coluna, onde por causa de sua rigidez relativa, os momentos são altamente concentrados, as diferenças entre cálculos manuais e otimização por S3D arredondam um valor de 10 – 15%. Essa praticidade indica uma excelente correspondência entre os procedimentos de análise e projeto.

Para tiras intermediárias, os resultados diferem um pouco mais porque o código só atribui o resto do momento depois de tirar as tiras de coluna correspondentes. Isso afetará a correspondência quando a compararmos com a análise do software, qual é mais preciso.

Novo no SkyCiv? Inscreva-se e experimente você mesmo o software!

Inscreva-se no SkyCiv!