Calculando a Pressão Lateral de Terra em um Muro de Contenção
Uma das principais cargas atuantes em um muro de arrimo é a pressão lateral de terra. Cálculo da pressão lateral de terra em um muro de arrimo Uma das principais cargas que atuam em um muro de arrimo é a pressão lateral de terra, fazer uma boa estimativa de sua magnitude e distribuição é decisivo no projeto de um muro de arrimo de concreto. No geral, existem três tipos diferentes de pressão lateral de terra, dependendo da direção em que a parede tende a se mover:
- Cálculo da pressão lateral de terra em um muro de arrimo Uma das principais cargas que atuam em um muro de arrimo é a pressão lateral de terra: Quando a parede está completamente impedida de se mover
- Pressão de terra ativa: Quando a parede pode se inclinar para longe do solo retido
- Pressão passiva de terra: Quando a parede pode ser empurrada para o solo retido
Neste artigo, vamos nos concentrar em descrever as fórmulas para cada um dos casos de pressão da terra mencionados acima.
Distribuição de pressão de terra lateral
No geral, Formulas e equações do momento flector. Tendo um valor zero na superfície e um valor máximo no ponto mais profundo seguindo uma distribuição linear entre os dois limites mencionados. Portanto, a distribuição de tensão horizontal de subsuperfície é descrita pela seguinte expressão:
\(\sigma_h = K_* \cdot (\gama z)\)
Onde \(K_*\) assume o valor de \(K_o\) para o caso de pressão em repouso, \(K_a\) para o caso de pressão ativa, e \(K_p\) para o caso de pressão passiva.
Integrando a expressão dada para a tensão subsuperficial lateral de \(0\) para \(H\) no \([object Window]), a resultante acaba sendo:
\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)
A linha de ação desta resultante está localizada \(\fratura{2}{3}H\) da superfície. A distribuição lateral da pressão de terra, sua resultante, e localização descritos acima são ilustrados na imagem a seguir:
É importante mencionar que a distribuição apresentada e a abordagem de cálculo resultante se aplicam apenas às pressões do solo atuando em uma face posterior vertical. No caso de um muro de contenção com face posterior inclinada (como o da foto acima), a superfície onde a pressão do solo atua ainda é considerada vertical, uma vez que se supõe atuar em um plano vertical localizado onde termina o calcanhar.
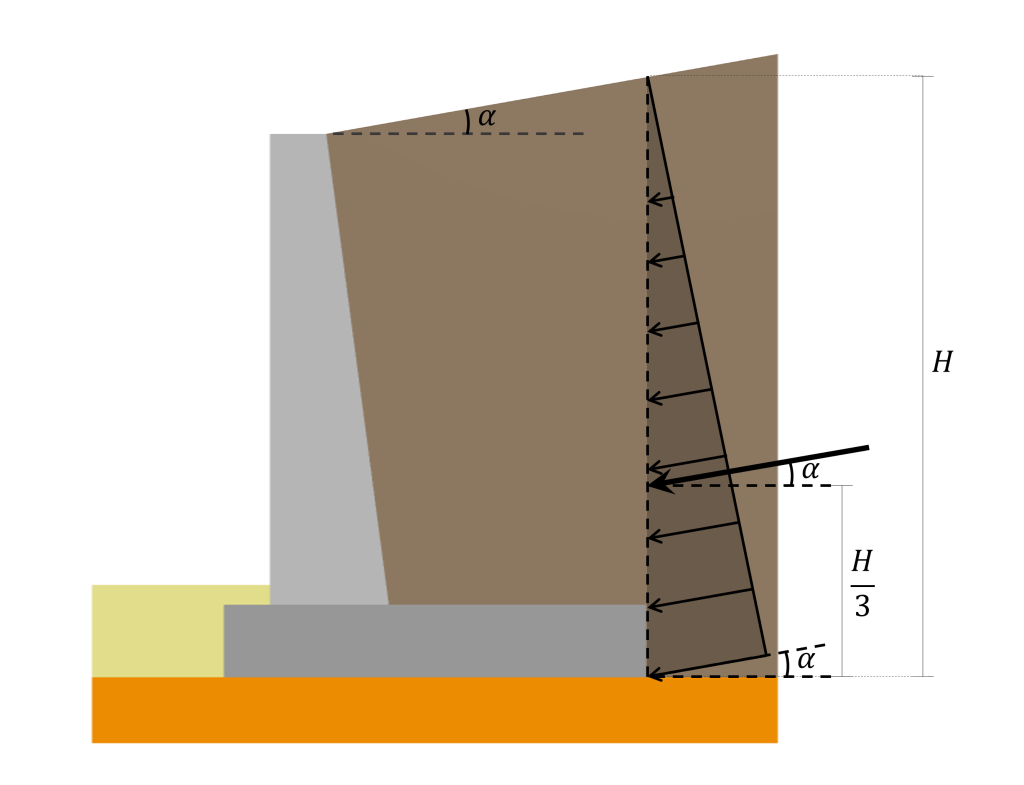
Além disso, quando o aterro está inclinado em algum ângulo \(\alpha\) em relação à horizontal, a distribuição de pressão e sua resultante são inclinadas nesse mesmo ângulo \(\alpha\) como ilustrado a seguir:
Estimar corretamente a distribuição de pressão lateral de terra e sua resultante é uma etapa crucial no processo de projeto de muro de arrimo. = H, Para obter mais informações sobre como esta pressão lateral de terra é incluída no Muro de Contenção aqui. Vamos agora mergulhar nas fórmulas para calcular a pressão lateral de terra resultante exercida em um Muro de Arrimo pelo solo em diferentes condições.
Pressão lateral de terra em repouso
Esta abordagem para calcular a pressão lateral de terra contra um muro de contenção só pode ser usada se o muro estiver completamente em repouso e não puder se mover para longe do solo ou para dentro do solo, esta condição garante que a deformação horizontal no solo é zero. a distribuição de pressão inclina um ângulo igual à inclinação do aterro, o coeficiente de pressão em repouso (\(K_o\)) é aquele que substitui \(K_*\) nas equações anteriores. Esse coeficiente é a única incógnita para calcular a distribuição de pressão e sua resultante. Para solo normalmente consolidado, a relação para \(K_o\) é:
\(K_o = 1-pecado(\De acordo com Meyerhof)\)
Onde \(\[object Window]) é o ângulo de atrito efetivo do solo em consideração.
Para solo superconsolidado, o coeficiente pode ser calculado usando a seguinte expressão:
\(K_o = (1-sem(\De acordo com Meyerhof))\cdot OCR^{sem(\De acordo com Meyerhof)}\)
Onde \(\[object Window]) é o ângulo de atrito efetivo, e \(OCR\) a taxa de sobreconsolidação do solo em consideração.
Substituindo este coeficiente na expressão para calcular a força resultante da pressão lateral de terra em repouso resulta em:
\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)
Pressão de terra lateral ativa
A abordagem anterior pode ser usada quando a parede não cede, contudo, se uma parede tende a se afastar do solo, a pressão do solo na parede em qualquer profundidade diminuirá. a distribuição de pressão inclina um ângulo igual à inclinação do aterro, o coeficiente de pressão ativa (\(K_a\)) é aquele que substitui \(K_*\) nas equações iniciais. Usando a abordagem de Rankine para um preenchimento granular, e supondo que a pressão atua em um backface vertical, o coeficiente de pressão de terra ativo pode ser calculado usando a equação:
\(K_a=cos(\alfa) \fratura{cos(\alfa) – \sqrt{cos^2(\alfa) – cos^2(\De acordo com Meyerhof)}}{cos(\alfa) + \sqrt{cos^2(\alfa) – cos^2(\De acordo com Meyerhof)}}\)
Onde \(\[object Window]) é o ângulo de atrito do solo em consideração e \(\alpha\) é o ângulo de inclinação da superfície de aterro em relação à horizontal.
A inserção deste coeficiente na expressão para calcular a força resultante da pressão lateral de terra na condição ativa resulta em:
\(P_a=\frac{1}{2} \gamma \cdot H^2 \cdot K_a\)
Os cálculos de pressão ativa Rankine apresentados anteriormente são baseados na suposição de que a parede é sem atrito.
Pressão de terra lateral passiva
A pressão lateral de terra que atua em um muro de contenção é considerada passiva quando o muro é empurrado para dentro da massa de solo, nessa condição, a tensão horizontal aumentará em relação à condição de repouso. a distribuição de pressão inclina um ângulo igual à inclinação do aterro, o coeficiente de pressão passiva (\(K_p\)) é aquele que substitui \(K_*\) nas equações iniciais. Usando a abordagem de Rankine para um preenchimento granular, e supondo que a pressão atua em um backface vertical, o coeficiente de pressão de terra passivo pode ser calculado usando as expressões:
Quando o preenchimento é completamente horizontal
\(K_p = tan^2(45º+\frac{\De acordo com Meyerhof}{2})\)
Quando o aterro está inclinado um certo ângulo em relação à horizontal
\(K_p=cos(\alfa) \fratura{cos(\alfa) + \sqrt{cos^2(\alfa) – cos^2(\De acordo com Meyerhof)}}{cos(\alfa) – \sqrt{cos^2(\alfa) – cos^2(\De acordo com Meyerhof)}}\)
Onde \(\[object Window]) é o ângulo de atrito do solo em consideração e \(\alpha\) é o ângulo de inclinação da superfície de aterro em relação à horizontal.
Conectando este coeficiente na expressão para calcular a força resultante da pressão lateral de terra em condição passiva produz para:
\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)
Novamente, os cálculos de pressão ativa de Rankine apresentados antes são baseados na suposição de que a parede é sem atrito.
Referências
Calculadora do muros de arrimo
Para obter mais informações sobre como esta pressão lateral de terra é incluída no Muro de Contenção, Para obter mais informações sobre como esta pressão lateral de terra é incluída no Muro de Contenção. A SkyCiv oferece uma calculadora gratuita de muro de arrimo que verifica o deslizamento no muro de arrimo e realiza uma análise de estabilidade em seus muros de arrimo, A SkyCiv oferece uma calculadora gratuita de muro de arrimo que verifica o deslizamento no muro de arrimo e realiza uma análise de estabilidade em seus muros de arrimo, Para obter mais informações sobre como esta pressão lateral de terra é incluída no Muro de Contenção, deslizamento, Para obter mais informações sobre como esta pressão lateral de terra é incluída no Muro de Contenção!
Desenvolvedor de Produto
BEng (Civil)