A walk-through and example of calculating snow drift loads and how to apply them
Projetos de telhado geralmente apresentam inúmeras elevações de telhado e raramente oferecem uma única altura de telhado. Por causa disso, existem áreas de telhado mais altas e mais baixas que as outras e estão sujeitas a montes de neve. A quantidade de carga de neve adicional, ou sobretaxa, can and will make a large impact of the design of the members in these areas.
Geometry of the roof and the direction of the wind are the two drivers that lead to snow drifts. The two directions of wind that cause snow drifts are “barlavento” e “sotavento”. Windward snow drifts occur when wind blows snow from a lower elevation roof towards the wall of an adjacent, telhado mais alto. Os montes de neve de sotavento ocorrem quando o vento leva a neve de um telhado de maior elevação para um telhado adjacente inferior. Veja a figura 7-7 de ASCE 7-10 below for a succinct depiction:

Lets assume our project is in Madison, Wisconsin and we have already calculated our balanced, roof snow load aqui. From our example, our ground load and flat roof snow load were found to be 30 psf e 21 psf, respectivamente. Provisions on how to calculate the snow drift surcharge for structures can be found in Section 7.8 de ASCE 7-10.
Our example structure’s roof has two varying roof heights and therefore we need to calculate the snow drift surcharge and apply it to our members. No nosso caso, our beams are spaced at 10 pés.
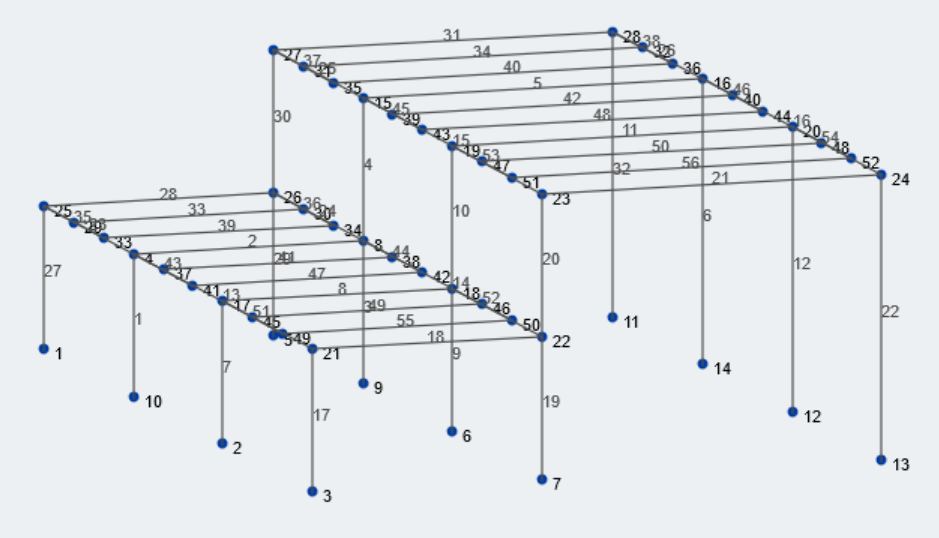
Figura 1: Isometric view of our example structure
Lets first gather the relevant geometric information about our structure. The lower bay and upper bay size is 25 feet and 37 pés, respectivamente. The lower and higher roof elevations are 15 feet and 30 feet from grade, respectivamente. Most of the geometric values can be associated with variables. Lets take a look at all the pertinent variables for this calculation.
\({p}_{g}\) cargas de neve no painel solar também devem ser consideradas
\({eu}_{você}\) = length of upper roof
\({eu}_{eu}\) = length of lower roof
\({h}_{d}\) = height of snow drift
\({C}\) = width of snow drift
\({h}_{b}\) = height of balanced snow load
\({h}_{c}\) = clear height from top of balanced snow load to closest point of adjacent roof
\({h}_{r}\) = height difference between roofs
\({p}_{s}\) = design snow load from Chapter 7
\({c}\) = snow density
\({p}_{d}\) = snow drift load
Take a look at Figure 7-8 de ASCE 7-10 for a depiction of many of these terms and what they visually represent:
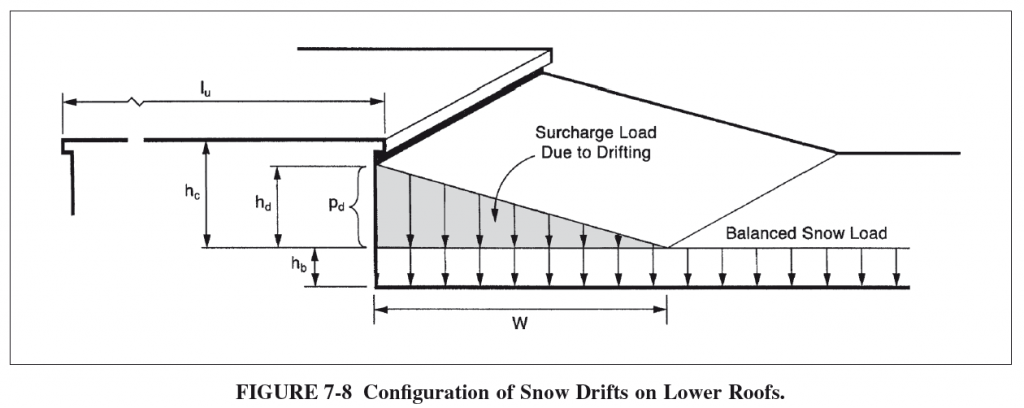
Finding the Snow Drift Surcharge Load
Now that we have identified what the variables are, the snow loading configurations, and the geometric constraints of our structure, lets calculate the snow drift.
Primeiro, find if snow drift loading is necessary, per ASCE 7.7-1:
A partir da elevação do solo gerada a partir das elevações do Google \({h}_{c}/{h}_{b} < 0.2\), then snow drift application is not necessary.
\({h}_{b} = {p}_{s}/{c}\), Onde:
\({c} = 0.13{p}_{g} + 14 ≤ 30 pcf\)
\({c} = 0.13*(30) + 14 = 17.9 pcf ≤ 30 pcf \)
\({h}_{b} = {21 psf}/{17.9 pcf} = 1.17 [object Window])
\({h}_{c} = {h}_{r}-{h}_{b}\)
\({h}_{c} = 15 ft – 1.17 ft = 13.8 [object Window])
\({h}_{c}/{h}_{b} = 13.8 ft/1.17ft = 11.8 > 0.2\) e portanto, snow drift loading is necessary.
Segundo, find maximum drift height between both windward and leeward directions:
The height of the drift for both wind directions can be found using the equation found in Figure 7-9 de ASCE 7-10, mostrado abaixo:
\({h}_{d} = 3/4*(0.43({eu}_{eu})^{1/3}({p_g}+10)^{1/4}-1.5)\) for windward drift
\({h}_{d} = 0.43({eu}_{você})^{1/3}({p_g}+10)^{1/4}-1.5\) for leeward drift
Windward drift height:
\({h}_{d} =3/4*(0.43(25 ft)^{1/3}(30 psf+10)^{1/4}-1.5)\)
\({h}_{d} = 1.25 [object Window])
Leeward drift height:
\({h}_{d} = 0.43(37 ft)^{1/3}(30 psf+10)^{1/4}-1.5\)
\({h}_{d} = 2.1 [object Window])
The maximum drift height between the windward and leeward drift height will be used for design, Portanto:
\({h}_{d} = 2.1 [object Window])
A continuação, find the width of the snow drift surcharge:
The width of the snow drift load, \({C}\), depends on \({h}_{c}\) e \({h}_{d}\)
Per Section 7.7.1,
A partir da elevação do solo gerada a partir das elevações do Google \({h}_{d} ≤ {h}_{c}\), então \({C} = 4{h}_{d}\)
A partir da elevação do solo gerada a partir das elevações do Google \({h}_{d} > {h}_{c}\), então \({C} = 4{h}_{d}^2/{h}_{c}) e subsequentemente \({h}_{d} = {h}_{c}\)
No nosso caso, \({h}_{c} = 13.8 [object Window]) e \({h}_{d} = 2.1 [object Window]), e portanto:
\({h}_{d} ≤ {h}_{c}\), e
\({C} = 4*(2.1 ft)\)
\({C} = 8.4 [object Window])
Observação, per ASCE 7-10 a snow drift width shall never exceed \(8{h}_{c}\)
Last, calculate the snow drift surcharge load:
To find the maximum surcharge load, multiply the drift height by the snow density:
\({p}_{d} = {h}_{d}{c}\)
No nosso caso,
\({p}_{d} = (2.1 ft)*(17.9 pcf)\)
\({p}_{d} = 37.6 [object Window])
The maximum snow drift surcharge load is then superimposed on the balanced snow load:
\({p}_{max} = {p}_{d}+{p}_{s}\)
\({p}_{max} = 58.6 [object Window])
Applying the Snow Drift Surcharge Loads
Lets look at the middle frame of our structure. The distributed area for the beams in this plane is 10 ft because of the constant 10 ft beam spacing. Figura 2 shown below depicts the balanced snow load of 21 psf applied to the roof of our structure. Observação, all values are unfactored, service loads.
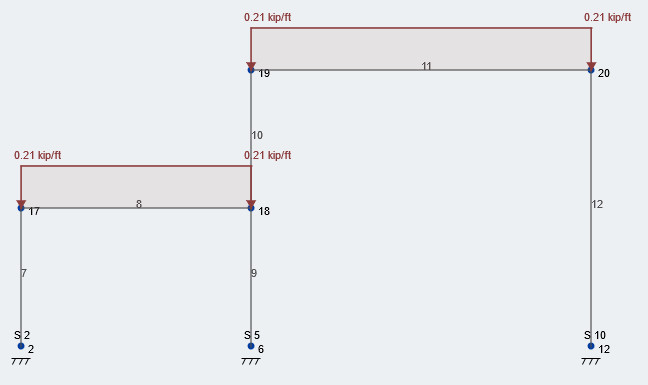
Figura 2: Typical loading condition of balanced snow load
Agora, lets take the snow drift surcharge load and superimpose it on our structure. Figura 3 depicts the additional drift load at the correct location. Como você pode ver, our total snow load is 58.6 psf – rounded up to 59 psf – located at the face of the wall and then decreases linearly over the 8.4 ft drift width back to the constant balanced snow load. This loading condition follows the entire length of the wall, in our course, the length of the structure.
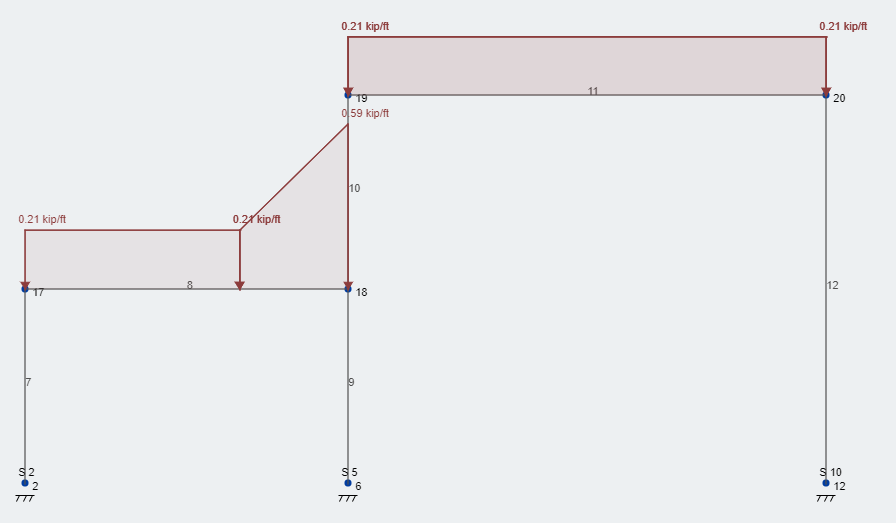
Figura 3: Typical loading condition service level snow design loads
At this point the snow loads are ready for analysis in conjuncture with other load cases and load combinations based on ASCE 7-10 and other pertinent building codes. Make sure to read through Chapter 7 de ASCE 7-10 for more information about successive provisions for partial snow loading and unbalanced snow loading, as those conditions were not evaluated here.
Referências:
- Cargas mínimas de projeto para edifícios e outras estruturas. (2013). EIXOS / SEIS 7-10. Sociedade Americana de Engenheiros Civis.

