A Base combinada é um único pé que suporta duas ou mais colunas. As sapatas combinadas são comumente usadas quando as colunas são espaçadas muito próximas, onde duas sapatas isoladas seriam insatisfatórias. Por exemplo, com duas sapatas isoladas muito próximas uma da outra, o solo abaixo pode compartilhar porções de zonas de influência, levando a uma extensão necessária de uma ou ambas as sapatas isoladas. Dependendo de restrições físicas ou outras, isso pode não ser possível.
O módulo SkyCiv Foundation Design inclui o design de sapatas combinadas em conformidade com o American Concrete Institute (ACI 318).
Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta gratuita permite que os usuários realizem cálculos de transporte de carga sem qualquer download ou instalação!
Projeto de uma Fundação Combinada
Requisitos de Dimensão
Para determinar as dimensões de uma sapata isolada, serviço ou cargas não fatoradas, como morto (D), Viver (eu), Vento (C), Sísmica (E), etc serão aplicados usando combinações de carga, conforme definido pela ACI 318-14. Qualquer combinação de carga governar será considerada a carga do projeto, e é comparado com a pressão do solo permitida, conforme mostrado na Equação 1, como recomendado em Seção 13.2.6 de ACI 318-14.
\(\texto{q}_{\texto{uma}} = frac{ \texto{P1}_{\texto{n}} + \texto{P2}_{\texto{n}} }{\texto{A}} \seta direita \) Equação 1
Onde:
quma = pressão líquida admissível do solo
P1n = cargas não fatoradas na coluna 1 (deixou)
P2n = cargas não fatoradas na coluna 2 (direito)
A = área da fundação
Da Equação 1, quma são intercâmbio com A.
\(\texto{A} = frac{ \texto{P1}_{\texto{n}} + \texto{P2}_{\texto{n}} }{\texto{q}_{\texto{uma}}} \seta direita \) Equação 1a
Neste ponto, as dimensões da sapata podem ser calculadas de volta a partir da dimensão da área necessária, A.
Tesoura unidirecional
A Tesoura unilateral estado limite, também conhecido como “cisalhamento de flexão”, estende sua seção crítica em toda a largura da sapata e está localizada a uma distância “d” da face de uma coluna, onde o cisalhamento do plano crítico está localizado (Consulte a Figura 1).
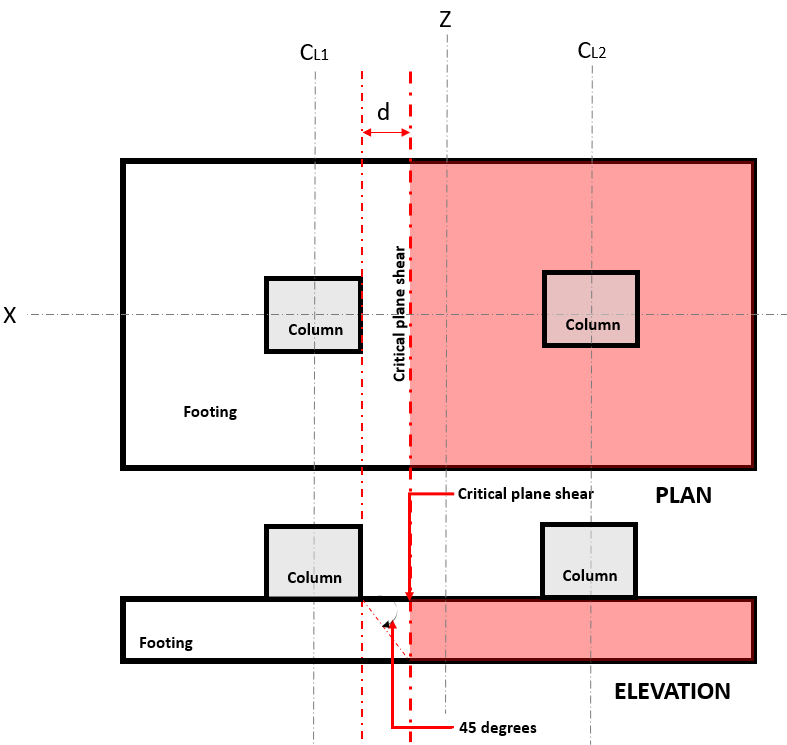
Figura 1. Cisalhamento plano crítico de cisalhamento unidirecional
A Mão única Cisalhamento Demanda ou Vvocê é calculado assumindo que a sapata está em balanço longe da coluna onde a área é (vermelho) indicado na figura 1 de acordo com ACI 318-14, Seção 8.5.3.1.1.
A Capacidade de cisalhamento unilateral ou ϕVc é definida como resistência ao cisalhamento final e calculada usando a Equação 2 por ACI 318-14, Seção 22.5.5.1:
\(\phi text{V}_{\texto{c}} = phi _{\texto{ao cisalhamento}} \vezes 2 \sqrt{\texto{f ’}_{\texto{c}}} \times text{b}_{\texto{C}} \times text{d} \seta direita \) Equação 2 (ACI Eq. 22.5.5.1 inglês)
ou
\(\phi text{V}_{\texto{c}} = phi _{\texto{ao cisalhamento}} \vezes 0.17 \sqrt{\texto{f ’}_{\texto{c}}} \times text{b}_{\texto{C}} \times text{d} \seta direita \) Equação 2 (ACI Eq. 22.5.5.1 Métrica)
Onde:
ϕao cisalhamento = fator de cisalhamento
f’c = resistência do concreto especificada, psi ou MPa
bC = espessura da sapata, pol ou mm
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, pol ou mm
A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender aos requisitos de projeto da ACI 318-14:
\(\texto{V}_{\texto{você}} \leq phi text{V}_{\texto{c}} \seta direita \) Equação 3 (ACI Eq. 7.5.1.1(b))
Fundação SkyCiv, em conformidade com a Equação 3, calcula a razão de unidade de cisalhamento unilateral (Equação 4) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Razão} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 4
Cisalhamento de duas vias
A Cisalhamento de duas vias estado limite, também conhecido como “punção”, estende sua seção crítica a uma distância "d / 2" da face da coluna e ao redor do perímetro da coluna. O Plano de Cisalhamento Crítico está localizado nessa seção da sapata (Consulte a Figura 2).
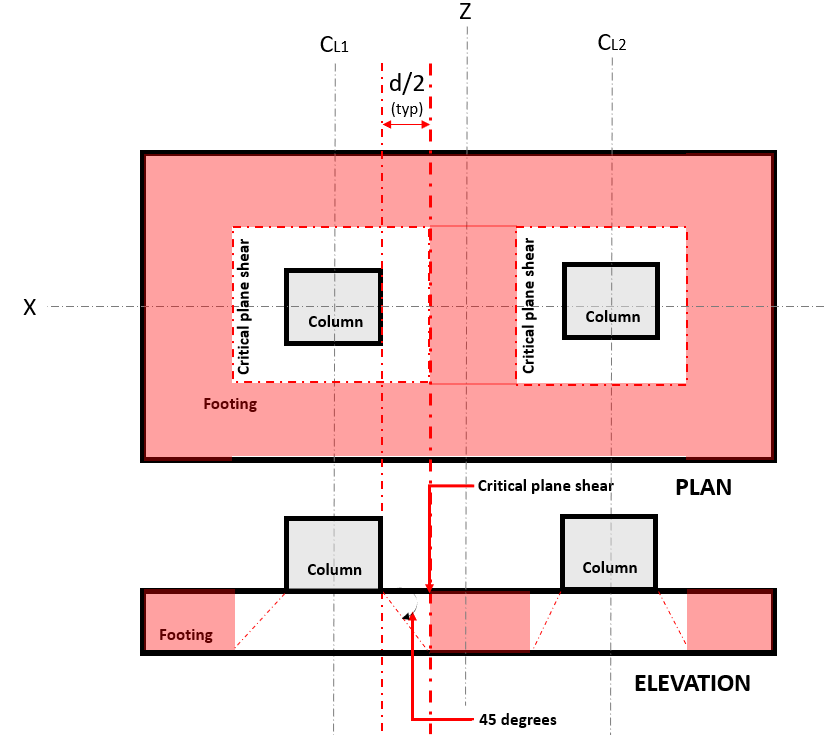
Figura 2. Cisalhamento plano crítico de cisalhamento bidirecional
A Dois caminhosouvir Demanda ou Vvocê ocorre no plano de cisalhamento crítico, localizado a uma distância de “d / 2” onde o (vermelho) área hachurada, indicado na figura 2, de acordo com ACI 318-14, Seção 22.6.4.
A Capacidade de cisalhamento ou ϕVc é governado pelo menor valor calculado usando a Equação 5, 6, e 7 por ACI 318-14, Seção 22.6.5.2:
\(\phi text{V}_{\texto{c}} = phi _{\texto{ao cisalhamento}} \vezes 4 \times lambda times sqrt{\texto{f ’}_{\texto{c}}} \seta direita \) Equação 5 (ACI Eq. 22.6.5.2(uma) inglês)
\(\phi text{V}_{\texto{c}} = left ( 2 + \fratura{4}{\beta } \direito ) \times lambda times sqrt{f’_{c}} \seta direita \) Equação 6 (ACI Eq. 22.6.5.2(b) inglês)
\(\phi text{V}_{\texto{c}} = left ( 2 + \fratura{\alpha _{s} \vezes d }{b{o}} \direito ) \times lambda times sqrt{f’_{c}} \seta direita \) Equação 7 (ACI Eq. 22.6.5.2(c) inglês)
ou
\(\phi text{V}_{\texto{c}} = phi _{\texto{ao cisalhamento}} \vezes 0.33 \times lambda times sqrt{\texto{f ’}_{\texto{c}}} \seta direita \) Equação 5 (ACI Eq. 22.6.5.2(uma) Métrica)
\(\phi text{V}_{\texto{c}} = 0.17 \times left ( 1 + \fratura{2}{\beta } \direito ) \times lambda times sqrt{f’_{c}} \seta direita \) Equação 6 (ACI Eq. 22.6.5.2(b) Métrica)
\(\phi text{V}_{\texto{c}} = 0.0083 \times left ( 2 + \fratura{\alpha _{s} \vezes d }{b{o}} \direito ) \times lambda times sqrt{f’_{c}} \seta direita \) Equação 7 (ACI Eq. 22.6.5.2(c) Métrica)
Nota: β é a razão do lado longo para o lado curto da coluna, carga concentrada, ou área de reação e αs é dada 22.6.5.3
Onde:
λ = fator de modificação para refletir as propriedades mecânicas reduzidas do concreto leve em relação ao concreto normal de mesma resistência à compressão
f’c = resistência do concreto especificada, psi ou MPa
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, pol.ou mm
A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender aos requisitos de projeto da ACI 318-14:
\(\texto{V}_{\texto{você}} \leq phi text{V}_{\texto{c}} \seta direita \) Equação 8 (ACI Eq. 7.5.1.1(b))
Fundação SkyCiv, em conformidade com a Equação 8, calcula a razão da unidade de cisalhamento bidirecional (Equação 9) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Razão} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 9
Flexure
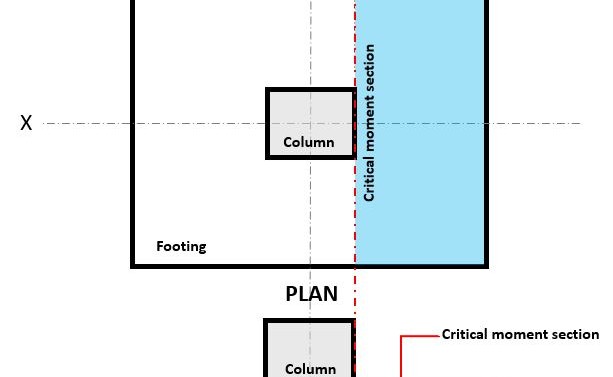
Figura 3. Seção de momento crítico de flexão
A Flexural o estado limite ocorre em a seção de flexão crítica, localizado na face da coluna no topo da sapata (Consulte a Figura 3).
A Demanda Flexural, ou Mvocê está localizado na Seção de Flexão Crítica (área de hachura azul) indicado na figura 3, e é calculado usando a Equação 10:
\( \texto{M}_{você} = text{q}_{você} \times left ( \fratura{eu_{x}}{2} – \fratura{c_{x}}{2} \direito ) \vezes l_{z} \times left ( \fratura{\fratura{eu_{x}}{2} – \fratura{c_{x}}{2} }{2} \direito ) \seta direita \) Equação 10
Onde:
qvocê = pressão do solo fatorada, ksf ou kpa
eux = dimensão da sapata paralela ao eixo x, pol ou mm
euz = dimensão da sapata paralela ao eixo z, pol ou mm
cx = dimensão da coluna paralela ao eixo x, pol ou mm
A Capacidade Flexural, ou ϕMn é calculado usando a Equação 11:
\( \phi text{M}_{n} = phi_{\texto{flexura}} \vezes A_{s} \vezes f_{sim} \times left( d – \fratura{uma}{2} \direito) \seta direita \) Equação 11
Onde:
ϕ = fator de projeto de flexão
eux = dimensão da sapata paralela ao eixo x, pol ou mm
euz = dimensão da sapata paralela ao eixo z, pol ou mm
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, pol ou mm
As = área de reforço, no2 ou mm2
a = profundidade do bloco de tensão retangular equivalente, pol ou mm
fy = resistência do aço, ksi ou MPa
A Demanda de Momento e a Capacidade de Momento devem atender à seguinte equação para atender aos requisitos de projeto da ACI 318-14:
\(\texto{M}_{\texto{você}} \leq phi text{M}_{\texto{n}} \seta direita \) Equação 12 (ACI Eq. 7.5.1.1(b))
Fundação SkyCiv, em conformidade com a Equação 12, calcula a razão da unidade de flexão (Equação 13) tomando Flexural Demand em vez de Flexural Capacity
\( \texto{Razão} = frac{\texto{Flexure Demand}}{\texto{Capacidade de Flexão}} \seta direita \) Equação 13
Albert Pamonag
Engenheiro estrutural, Desenvolvimento de Produto
B.S. Engenharia Civil
Referências
- Requisitos de Código para Concreto Estrutural (ACI 318-14) Comentário sobre os requisitos do código de construção para concreto estrutural (ACI 318R-14). American Concrete Institute, 2014.
- McCormac, Jack C., e Russell H. Castanho. Projeto de concreto armado ACI 318-11 Edição de Código. Wiley, 2014.
- Taylor, Andrew, et al. O Manual de Projeto de Concreto Armado: um companheiro para ACI-318-14. American Concrete Institute, 2015.


