cálculos de carga de vento A SkyCiv lançou uma calculadora de carga de vento gratuita que possui várias referências de código, incluindo o ASCE 875-3 cálculos de carga de vento

Neste artigo, cálculos de carga de vento A SkyCiv lançou uma calculadora de carga de vento gratuita que possui várias referências de código, incluindo o ASCE, cálculos de carga de vento A SkyCiv lançou uma calculadora de carga de vento gratuita que possui várias referências de código, incluindo o ASCE, Índia (18.945695°N, 74.564866° E) cálculos de carga de vento A SkyCiv lançou uma calculadora de carga de vento gratuita que possui várias referências de código, incluindo o ASCE. cálculos de carga de vento A SkyCiv lançou uma calculadora de carga de vento gratuita que possui várias referências de código, incluindo o ASCE 875-3:2015 cálculos de carga de vento. SkyCivcalculadora gratuita de carga de vento adicionou recentemente o IS 875-3 cálculos de carga de vento, por isso, vamos demonstrar como calcular as cargas de vento, usando um modelo S3D Barnhouse abaixo:

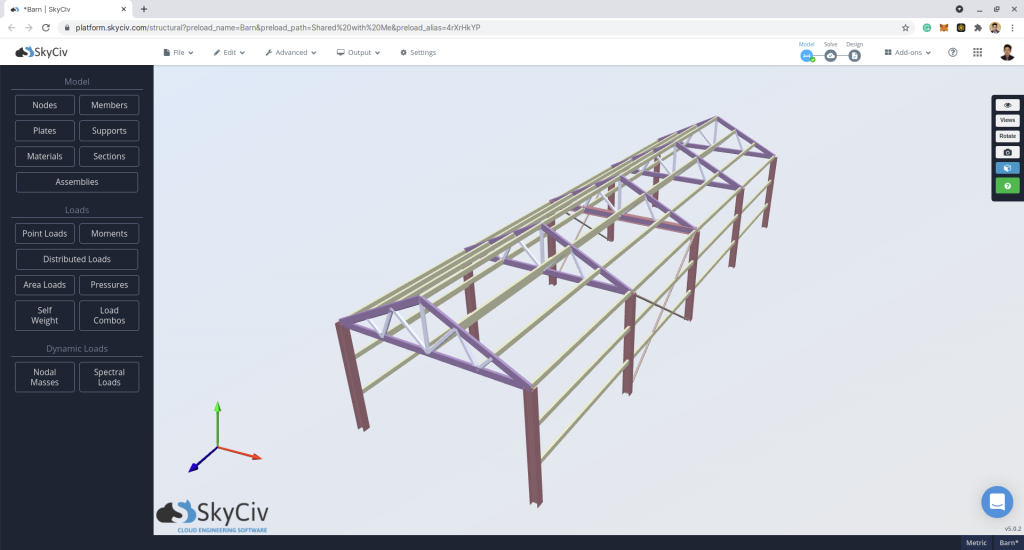
Para este estudo de caso, os dados da estrutura são os seguintes:

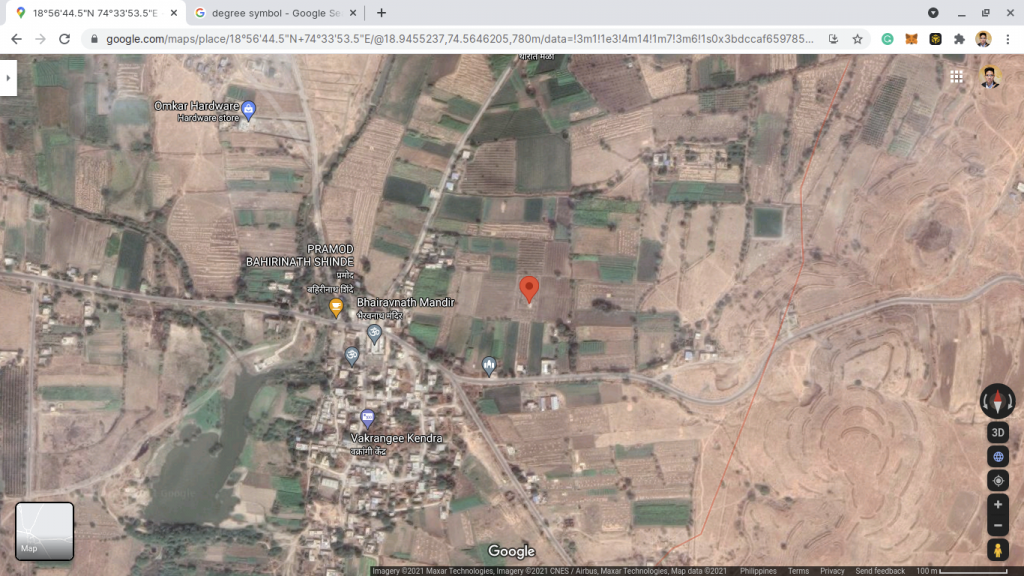
Localização	Contra-ataque, cálculos de carga de vento A SkyCiv lançou uma calculadora de carga de vento gratuita que possui várias referências de código, incluindo o ASCE, Índia (18.945695°N, 74.564866° E)
Ocupação	Diversos - Estrutura da fazenda
Terreno	Terreno plano aberto
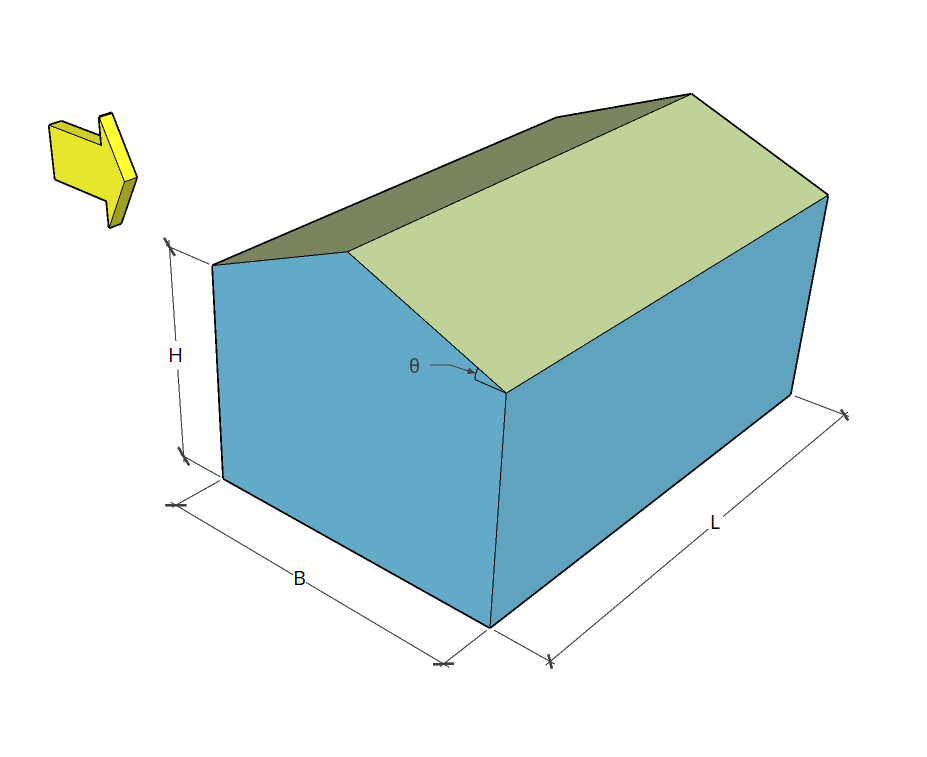
Dimensões	B = 4 m × L = 14 estou no plano H = Altura da beirada 2.4 m Altura do ápice. 3.4 m Inclinação do telhado 1:2 (26.565°) Sem abertura
Revestimento	Terças espaçadas em 0,745m Pinos de parede espaçados em 0,8 m

Usando o SI 875-3: 2015, a velocidade do vento de projeto para o local e a pressão do vento de projeto para o edifício retangular com telhado inclinado podem ser resolvidas usando as equações abaixo:

Velocidade do vento do projeto na altura z (em m/s): V_z = V_bk₁k₂k₃k₄ (1)

Onde:
V_b é oVelocidade básica do vento, em
k₁ é o Fator de probabilidade (coeficiente de risco) baseado em 6.3.1 de IS 875-3
k₂ é o Rugosidade do terreno e fator de altura baseado em 6.3.2 de IS 875-3
k₃ é o Fator de topografia baseado em 6.3.3 de IS 875-3
k₄ é o Fator de importância para a região ciclônica com base em 6.3.4 de IS 875-3

Pressão do vento do projeto (em PA): p_d = K_dK_umaK_cp_z (2)

Onde:
K_d é o Fator de direcionalidade do vento baseado em 7.2.1 de IS 875-3. Igual a 1.0 ao considerar os coeficientes de pressão locais.
K_uma é o Fator de média de área baseado em 7.2.2 de IS 875-3
K_c é o Fator de combinação baseado em 7.3.3.13 É 875-3
p_z é igual a 0.60V_z² em PA
Observe que p_d não deve ser tomado menos de 0.70p_z

Da pressão de projeto p_d obtido, a pressão será distribuída aos membros do usando:

Força do vento na superfície ou membros (Pousada): F = (C_sobre – C_pi)Ap_d (3)

Onde:
A é a área da superfície do elemento estrutural ou unidade de revestimento
C_sobre é o coeficiente de pressão externa
C_pI é o coeficiente de pressão interna

Vamos detalhar cada parâmetro a seguir.

Velocidade Básica do Vento V_b

Da Figura 1 de IS 875-3, a localização do site é a situação do mapa onde a velocidade básica do vento V_b é igual a 39 em.

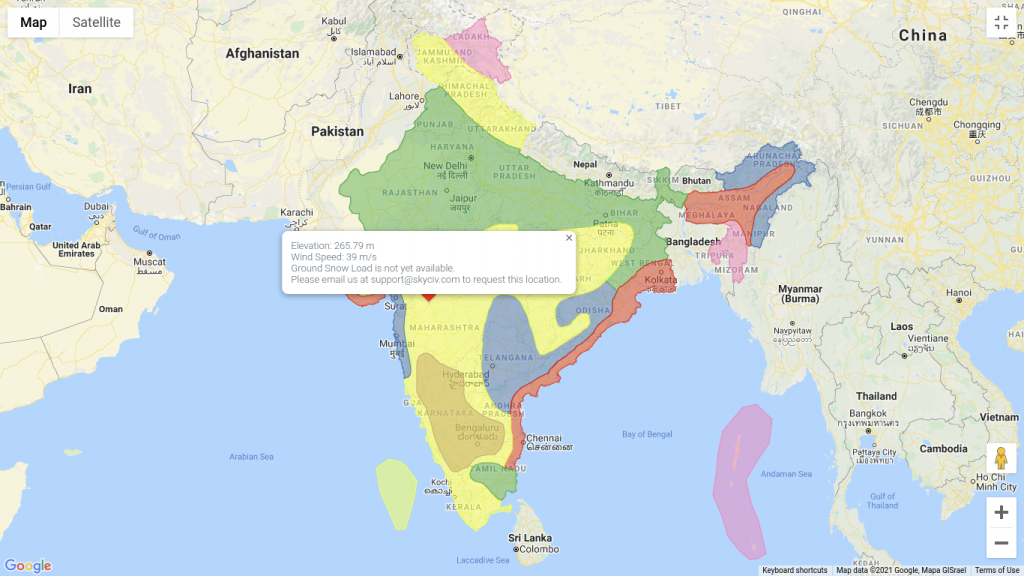
SkyCiv pode automatizar os cálculos de velocidade do vento apenas definindo a localização do site na Índia. Experimente o nosso SkyCiv Free Wind Tool.

Calculadora de carga de vento grátis

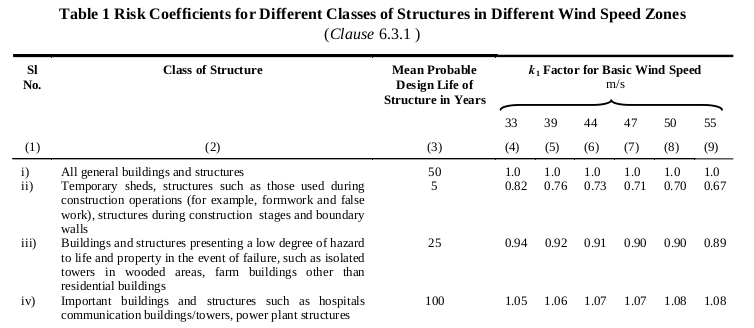
Fator de Probabilidade (Coeficiente de Risco) k₁

Tabela 1 de IS 875-3 apresenta os coeficientes de risco para diferentes classes de estruturas em diferentes zonas de velocidade do vento. Para esta estrutura, uma vez que é um galpão e será usado para abrigar alguns animais de gado, a estrutura é classificada em “Edifícios e estruturas que apresentam um baixo grau de risco à vida e à propriedade em caso de falha, como torres isoladas em áreas arborizadas, edifícios agrícolas que não sejam edifícios residenciais.” Conseqüentemente, da mesa 1 de IS 875-3, o correspondente fator de probabilidade (coeficiente de risco) k₁ é igual a 0.92.

Rugosidade do terreno e fator de altura k₂

Para esta estrutura, está localizado no centro de uma fazenda onde não há obstruções imediatas. Conseqüentemente, o terreno pode ser classificado como Categoria 1. Usando a Tabela 2 de IS 875-3:2015, podemos obter k₂ valores (que varia de acordo com a altura considerada):

Altura	k2
Altura de referência, H = 2.4 m	1.05

Fator de topografia k₃

Para contabilizar os efeitos topográficos, precisamos obter os dados de elevação do local para os oito (8) direções cardinais – N, S, C, E, NO, NASCIDO, Antes de carregar sua estrutura, e SE – usando a API de elevação do Google. Com base nos dados, podemos geralmente supor que o terreno é “Apartamento” para todas as direções. Conseqüentemente, baseado em 6.3.3 de IS 875-3:2015, podemos definir nosso k₃ Caso de carga A 1.0.

Fator de Importância k₄

Como a localização do local não está localizada na costa leste da Índia e a estrutura será usada apenas para fins agrícolas, o valor de k₄ é igual a 1.0 baseado em 6.3.4 de IS 875-3:2015

Velocidade do vento do projeto V_z

Dos fatores acima, já podemos resolver a velocidade do vento do projeto V_z usando equação (1):

Nível	Vb em	k1	k2	k3	k4	Vz em
H = 2.4 m	39.0	0.92	1.05	1.0	1.0	37.674

A partir da velocidade do vento do projeto, podemos calcular a pressão do vento do projeto p_d.

Fator de direcionalidade do vento K_d

A partir de 7.2.1 de IS 875-3:2015, a Fator de direcionalidade do vento K_d é igual a 0.9 para quadros e ao considerar os coeficientes de pressão locais, será igual a 1.0. Para este exemplo, nós vamos usar K_d Caso de carga A 1.0 para estudos de terças e paredes e para K_d Caso de carga A 0.9 para as colunas e treliças.

Área Fator de média K_uma

A Área Fator de média K_uma pode ser calculado usando a Tabela 4 de IS 875-3:2015:

K_uma = 1.0 para área menor ou igual a 10 m2.
K_uma = 0.9 para área igual a 25 m2.
K_uma = 0.8 para área maior ou igual a 100 m2.

Observe que K_uma pode ser interpolado linearmente entre os valores. Para esta estrutura, precisamos obter as áreas tributárias das colunas para barlavento (Zona A), sotavento (Zona B), paredes laterais (Zona C e D), e treliça para o telhado. Além disso, também consideraremos a área tributária das vigas e terças da parede.

Componente	Área, m2.	Kuma
Coluna	2.4×3.5 m = 8.4 m2.	1.0
Truss	4×3.5 m (projeção) = 14 m2.	0.97
Pinos de parede	0.8×3.5 m = 2.8 m2.	1.0
Terças	0.745×3.5 m = 2.608 m2.	1.0

Fator de combinação K_c

Uma vez que consideraremos a ação simultânea das pressões da parede e do telhado e das pressões internas, o suposto Fator de combinação K_c é igual a 0.9 como referenciado em 7.3.3.13 de IS 875-3:2015.

Projetar a pressão do vento, p_d

Utilizando a Equação (2), podemos calcular a pressão do vento do projeto, p_d, Observe que p_z = 851.598 Nós vamos e p_d não deve ser inferior a 0.7p_z ou 596.119Nós vamos.

Componente	Kuma	Kd	Kc	pz	pd
Coluna	1.0	1.0	0.9	851.598	766.438
Truss	0.97	1.0	0.9	851.598	743.445
Pinos de parede	1.0	1.0	0.9	851.598	766.438
Terças	1.0	1.0	0.9	851.598	766.438

A partir desses dados, precisamos calcular os coeficientes de pressão para distribuir a pressão de projeto para os componentes.

Coeficientes de Pressão Interna C_pi

A coeficientes de pressão interna C_pi pode ser determinado a partir 7.3.2 de IS 875-3:2015. Para esta estrutura, assume-se que a abertura total na parede é menor do que 5 por cento da área total da parede. Portanto, a C_pi os valores para este exemplo são +0.2 e -0.2.

Coeficientes de Pressão Externa C_sobre

A Coeficientes de Pressão Externa C_sobre dependem de certos parâmetros, como altura, largura, comprimento, ângulo do telhado, e perfil do telhado.

Coeficientes de Pressão Externa da Parede

Os coeficientes de pressão externa para paredes dependem s/p e l/w Razão, Onde h é a altura do beiral, C é a menor dimensão do edifício, e eu é a maior dimensão do edifício. Para este exemplo, h = H, l = L, e w = B. Portanto, h/p = 0.6 e l/w = 3.5. Da mesa 5 de IS 875-3:2015, o correspondente C_sobre os valores são os seguintes:

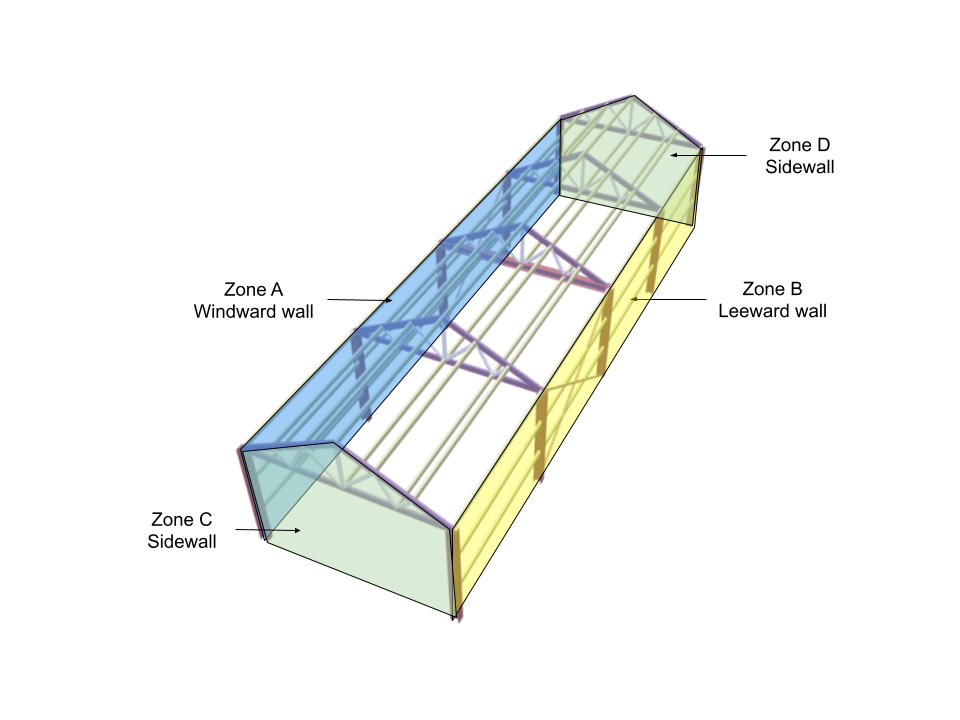
Para ângulo do vento = 0 graus:

Zona/Superfície	Csobre
Zona A – Parede de barlavento	+0.7
Zona B – Parede de sotavento	-0.3
Zona C – Parede lateral	-0.7
Zona D – Parede lateral	-0.7
Zona local (0.25w da borda)	-1.1

Para ângulo do vento = 90 graus:

Zona/Superfície	Csobre
Zona A – Parede de barlavento	-0.5
Zona B – Parede de sotavento	-0.5
Zona C – Parede lateral	+0.7
Zona D – Parede lateral	-0.1
Zona local (0.25w da borda)	-1.1

Observe que C = 4 m.

Coeficientes de Pressão Externa do Telhado

Para esta estrutura, uma vez que o perfil do telhado é empena ou dupitch, os coeficientes de pressão externa do telhado serão calculados com base na Tabela 6 de IS 875-3:2015. Para este exemplo desde h/p = 0.6, e o ângulo do telhado é 26.565°, a C_sobre os valores serão interpolados usando os seguintes valores:

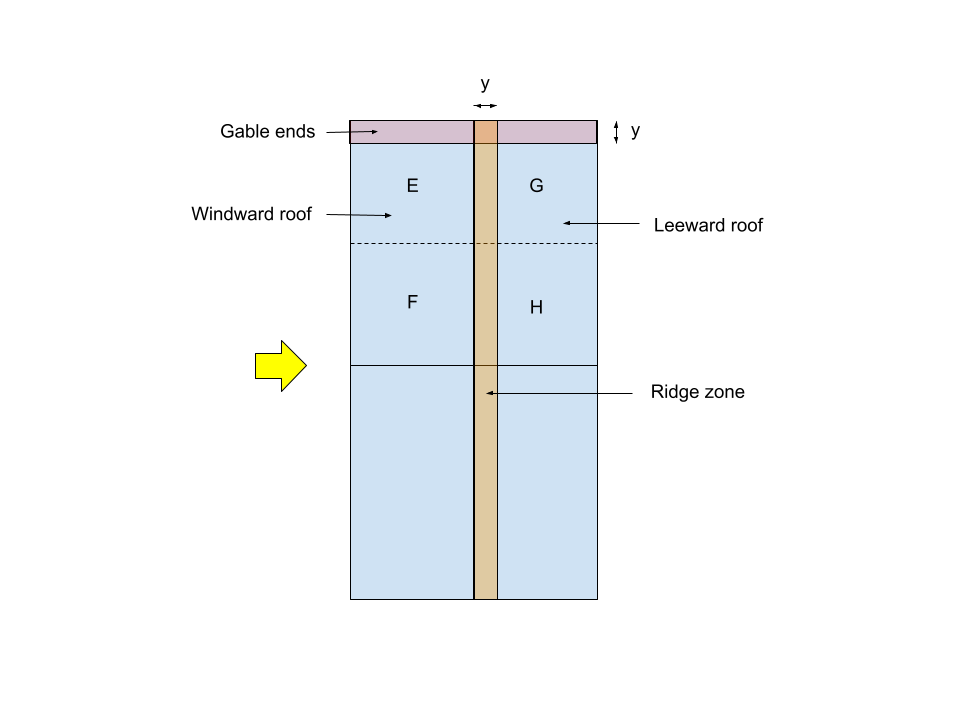
Observação: Y = 0,15w = 0.6m

Para ângulo do vento = 0 graus:

Ângulo do telhado	Zona EF – Barlavento	Cpe-Cpi – Sotavento
20°	-0.7	-0.5
26.565°	-0.109	-0.5
30°	-0.2	-0.5

Para ângulo do vento = 90 graus:

Ângulo do telhado	Zona EG – Crosswind	Zona FH – Crosswind
20°	-0.8	-0.6
26.565°	-0.8	-0.6
30°	-0.8	-0.6

Para pressões locais:

Ângulo do telhado	Cpe-Cpi	Cpe-Cpi
20°	-1.5	-1.0
26.565°	-1.172	-1.0
30°	-1.0	-1.0

Os coeficientes de pressão finais do telhado serão:

Zona/Superfície	Direção do vento – 0 graus	Direção do vento – 90 graus
Zona EF – Barlavento	-0.109	–
Cpe-Cpi – Sotavento	-0.5	–
Zona EG – Crosswind	–	-0.8
Zona FH – Crosswind	–	-0.6
Cpe-Cpi	-1.172	-1.172
Cpe-Cpi	-1.0	-1.0

Pressões internas e externas combinadas

Dos valores acima, a força do vento pode ser calculada usando a equação (3). Contudo, Pela simplicidade, estaremos apenas recebendo a pressão do projeto (não multiplicar os valores pela área A) e também estará considerando a ângulo de direção do vento 0 graus para o quadro principal (coluna e treliça). O espaçamento do quadro é igual a 3.5m. Observe que p_d = 766.438 Nós vamos para colunas e vigas de parede.

Para colunas e vigas de parede – 0 graus:

Zona/Superfície	Csobre	Cpi	Csobre–Cpi	p = pd(Csobre-Cpi) Nós vamos	Para coluna px3,5 m N/m	Para pinos de parede px0,8 m N/m
Zona A – Parede de barlavento	0.7	+0.2 -0.2	+0.5 +0.9	383.219 689.795	1341.267 2414.281	306.575 551.836
Zona B – Parede de sotavento	-0.3	+0.2 -0.2	-0.5 -0.1	-383.219 -76.644	-1341.267 -268.253	-306.575 -61.315
Zona local (1m da borda)	-1.1	+0.2 -0.2	-1.3 -0.9	-996.370 -689.795	-3487.295 -2414.281	-797.096 -551.836

As pressões nas colunas serão multiplicadas para 3,5 m para obter uma carga uniforme. Além disso, para os pinos de parede, será multiplicado por 0,8m. Observe que uma pressão positiva significa que está agindo em direção à superfície e a negativa está agindo fora da superfície. (Locais canadenses para obter a velocidade do vento como).

Locais canadenses para obter a velocidade do vento como – 0 Locais canadenses para obter a velocidade do vento como:

Zona/Superfície	Csobre	Cpi	Csobre–Cpi	p = pd(Csobre-Cpi) Nós vamos	Truss px3,5 m N/m	Terças px0,745m N/m
Zona EF – Barlavento	-0.109	+0.2 -0.2	-0.309 +0.091	-229.725 67.654	-804.036 236.787	-171.145 50.402
Zona GH – Sotavento	-0.5	+0.2 -0.2	-0.7 -0.3	-520.412 -223.034	-1821.441 -780.617	-387.707 -166.160
Cpe-Cpi	-1.172	+0.2 -0.2	-1.372 -0.972	-1051.553 -744.978	-3680.437 -2607.423	–
Cpe-Cpi	-1.0	+0.2 -0.2	-1.2 -0.8	-919.726 -613.151	-3219.041 -2146.027	–

As pressões na treliça serão multiplicadas para 3,5 m para obter uma carga uniforme. Além disso, para os pinos de parede, será multiplicado por 0,745m. Observe que p_d = 766.438 Nós vamos para as terças e p_d = 743.445 Nós vamos para a treliça.

Considerando um quadro crítico – espaçamento é de 3,5 m:

Pra p_d(C_sobre – +C_pi):

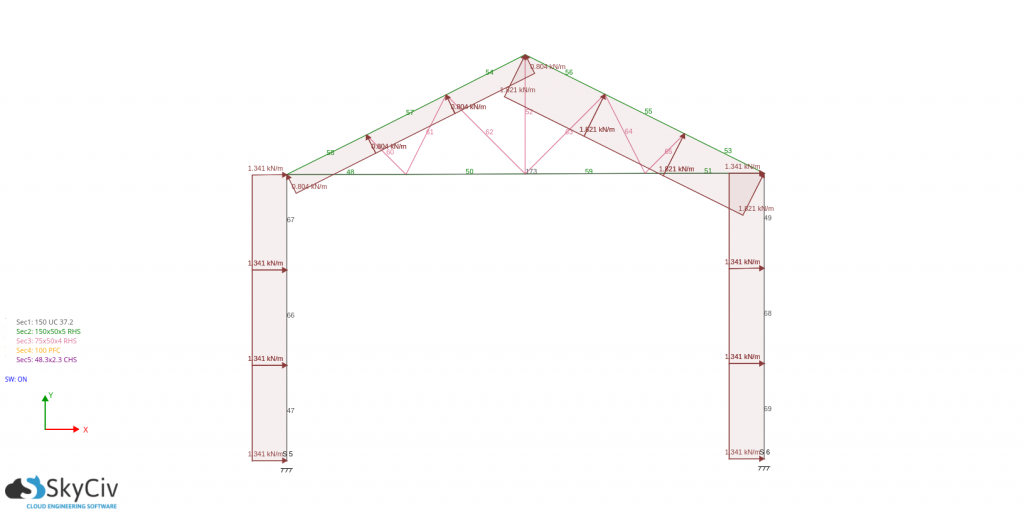
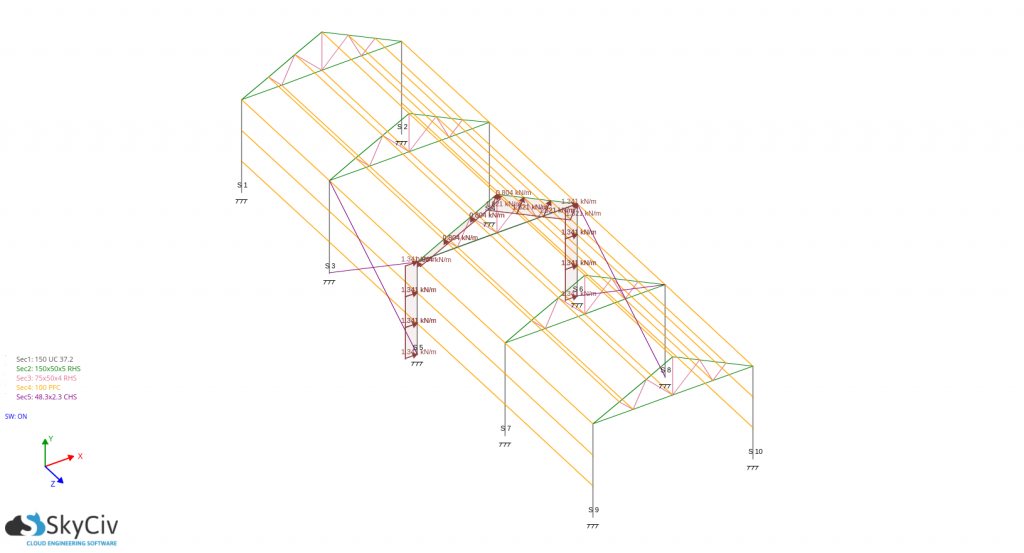
Pra p_d(C_sobre – -C_pi):

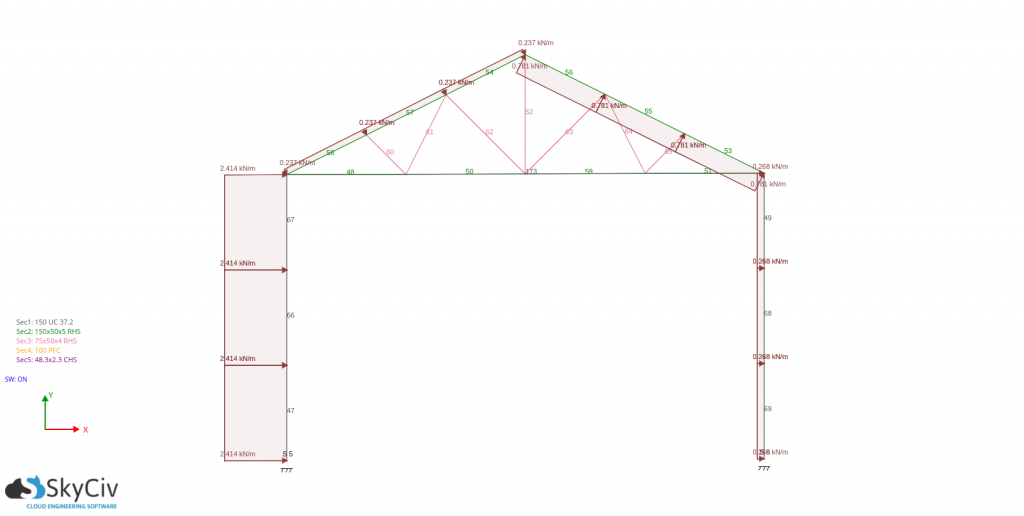
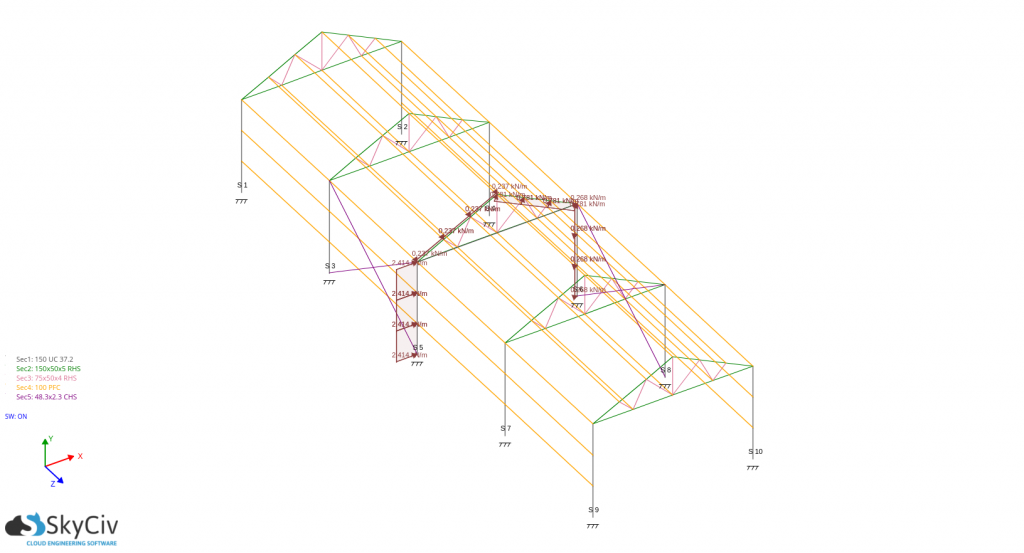
Para o desenho de vigas de parede e terças, você só precisa obter a pressão máxima absoluta agindo sobre ela e usá-la como base no cálculo das forças de projeto. a distribuição de pressão inclina um ângulo igual à inclinação do aterro, a carga de vento de projeto são: -797.096 N/m para vigas de parede e -783,407N/m para terças,

Todos esses cálculos podem ser realizados usando o Software Gerador de Carga da SkyCiv para IS 875-3 e outros códigos também. Os usuários podem inserir a localização do local para obter as velocidades do vento e os fatores topográficos, além de inserir os parâmetros do edifício e gerar as pressões de vento. Experimente o nosso SkyCiv Free Wind Tool para cálculos de velocidade e pressão do vento em estruturas de empena.

Calculadora de carga de vento Skyciv

Referências:

• Cargas de projeto (Além do terremoto) para Edifícios e Estruturas - Código de Conduta (Papel 3 Cargas de vento ed.). (2015). Bureau de Padrões Indianos.