Um exemplo totalmente trabalhado de cálculo de carga de vento para sinais usando EN 1991-1-4
Neste artigo, estaremos discutindo como calcular as cargas de vento em placas usando EN 1991-1-4 localizado em Oxfordshire, Reino Unido. Nossas referências serão o EN 1991-1-4 Ação em estruturas (carga de vento) e BS EN 1991-1-4 Anexo Nacional. Usaremos dados semelhantes em EN 1991-1-4 Exemplo de cálculo de carga de vento.
Um exemplo totalmente trabalhado de montagem no solo. Experimente o nosso Calculadora de Carga de Vento de Tabuleta:
Dados de Estrutura
Neste exemplo, usaremos os dados abaixo. Vamos considerar apenas direção da fonte de vento igual a 240°. além disso, a a elevação do terreno do local é de 57,35m.
Mesa 1. Os dados da placa de sinalização necessários para o cálculo da carga de vento.
| Localização | Oxfordshire, Reino Unido |
| Ocupação | Diversos – Tabuleta |
| Terreno | Fazenda plana |
| Dimensão horizontal do sinal, b | 12.0 m |
| Sinal Horizontal Vertical, h |
12.0 m |
| Terra ao topo da placa, H |
50.0m |
| Aterramento para centroide da placa, ze |
44.0 m |
| Área de referência da placa Aplaca |
144.0 m2. |
| Diâmetro do poste, d |
1.0 m |
| Tipo de superfície do poste |
Ferro fundido |
| Terra ao topo do poste, zg |
38.0 m |
| Área de referência do pólo Apólo |
38.0 m |
Figura 1. Localização do site (do Google Maps).

Figura 2. Dimensões da placa.
A fórmula para determinar a pressão do vento do projeto é:
Para velocidade básica do vento:
\({v}_{b} = {c}_{para você} {c}_{estação} {c}_{alt} {v}_{b,mapa}\) (1)
Onde:
\({v}_{b}\) = velocidade básica do vento em m / s
\({c}_{para você}\) = fator direcional
\({c}_{estação}\)= fator sazonal
\({c}_{alt}\)= fator de altitude onde:
\({c}_{alt} = 1 + 0.001A \) pra \( z ≤ 10 \) (2)
\({c}_{alt} = 1 + 0.001A ({10/z}^{0.2}) \) pra \( z > 10 \) (3)
\({v}_{b,mapa}\) = valor fundamental da velocidade básica do vento dado na Figura NA.1 da BS EN 1991-1-4 Anexo Nacional
\( A \) = altitude do local em metros acima do nível médio do mar
Para pressão de velocidade básica:
\({q}_{b} = 0.5 {⍴}_{ar} {{v}_{b}}^{2} \) (4)
Onde:
\({q}_{b}\) = pressão do vento projetada em Pa
\({⍴}_{ar}\) = densidade do ar (1.226kg / cu.m.)
\({v}_{b}\)= velocidade básica do vento em m / s
Para pressão de pico:
\({q}_{p}(z) = 0.5 {c}_{e}(z){q}_{b} \) para local em terreno rural (5)
\({q}_{p}(z) = 0.5 {c}_{e}(z){c}_{e,T}{q}_{b} \) para local no terreno da cidade (6)
Onde:
\({c}_{e}(z)\) cargas de neve no painel solar também devem ser consideradas
\({c}_{e,T} \) = fator de correção de exposição para o terreno da cidade
Para calcular a força do vento que atua na placa/poste:
\({F}_{C} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({z}_{e}){A}_{referência} \) (7)
Onde:
\( {c}_{s} {c}_{d} \) = fator estrutural
\({c}_{f} \) = coeficiente de força da estrutura
\({q}_{p}({z}_{e}) \) = pressão de velocidade de pico na altura de referência \({z}_{e} \)
\({A}_{referência} = b h\) = área de referência da estrutura
Categoria de Terreno
Baseado em BS EN 1991-1-4 Anexo Nacional, as Categorias de Terreno em EN 1991-1-14 foram agregados em 3 categorias: Categoria de terreno 0 é conhecido como mar; As categorias de terreno I e II foram consideradas como terreno do país, e as categorias de terreno III e IV foram consideradas como terreno da cidade.
Considerando vento vindo de 240°, podemos classificar a categoria de terreno do terreno a favor do vento como Terreno da cidade.
Fatores direcionais e sazonais, \({c}_{para você}\) & \({c}_{estação}\)
A fim de calcular para a Equação (1), precisamos determinar os fatores direcionais e sazonais, \({c}_{para você}\) & \({c}_{estação}\). Da Tabela NA.1 da BS EN 1991-1-4 Anexo Nacional, uma vez que a direção da fonte de vento é 240°, o valor correspondente para o fator direcional, \({c}_{para você}\), é igual a 1.0.

Por outro lado, queremos considerar um caso conservador para o fator temporada, \({c}_{estação}\), que nós vamos definido como 1.0.
Fator de Altitude \({c}_{alt}\)
Para o fator altitude, \({c}_{alt}\), usaremos apenas a equação (2) para uma abordagem mais conservadora usando a elevação do local \( A \) igual a 57,35m. Portanto:
\({c}_{alt} = 1 + 0.001(57.35) = 1.05735\)
Velocidade e pressão básicas do vento, \({v}_{b}\) & \({q}_{b}\)
O mapa de velocidade do vento para o Reino Unido pode ser obtido a partir da Figura NA.1 do Anexo Nacional para BS EN 1991-1-4.
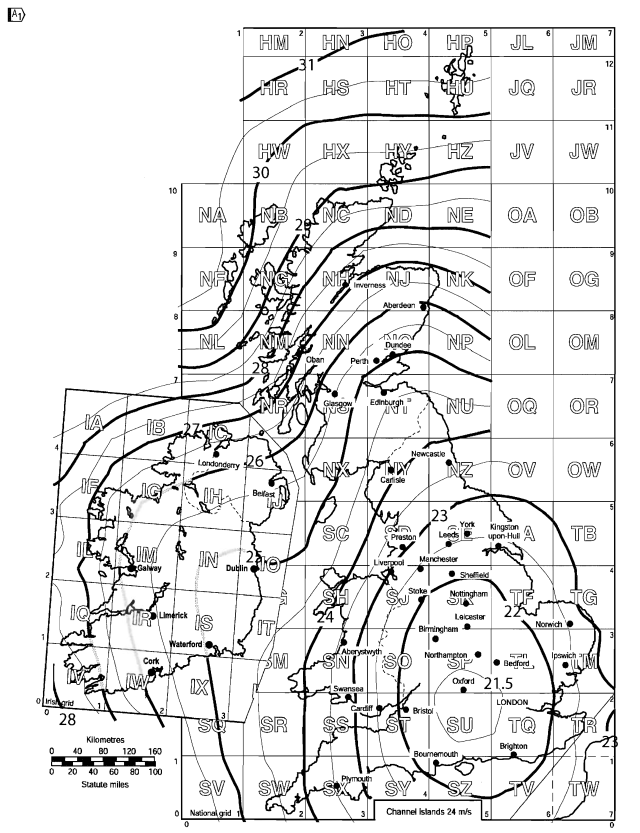
Figura 5. Velocidade básica do vento para o Reino Unido com base na Figura NA.1 da BS EN 1991-1-4 Anexo Nacional.
Para a localização do nosso site, Oxfordshire, Inglaterra, o calculado \( {v}_{b,mapa} \) é igual a 22.7 em.
\( {v}_{b} = {c}_{para você} {c}_{estação} {c}_{alt} {v}_{b,mapa} = (1.0)(1.0)(1.05735)(22.7) \)
\( {v}_{b} = 24.0 em \)
Podemos calcular a pressão básica do vento, \( {q}_{b,0} \), usando equações (4):
\( {q}_{b} = 0.5(1.226)({24}^{2}) = 353.09 Nós vamos \)
SkyCiv agora automatiza a detecção da região do vento e obtém o valor da velocidade do vento correspondente com apenas algumas entradas. Experimente o nosso SkyCiv Free Wind Tool
Fator de orografia \({c}_{o}(z)\)
Para esta estrutura, o terreno é relativamente plano para o vento vindo de 240°, a
fator de altitude, \({c}_{alt}\), usaremos apenas a equação (2) para uma abordagem mais conservadora usando a elevação do local \( A \) igual a 57,35m. Portanto:
Pressão de Velocidade de Pico, \({q}_{p}(z)\)
Para nossa estrutura, uma vez que a categoria de terreno é classificada como terreno de cidade, o pico Da mesma forma, a pressão de pico de velocidade, \({q}_{p}(z)\), pode ser resolvido usando a equação (6):
\({q}_{p}(z) = {c}_{e}(z){c}_{e,T}{q}_{b} \)
Onde:
\({c}_{e}(z)\) = fator de exposição com base na Figura NA.7 da BS EN 1991-1-4 Anexo Nacional
\({c}_{e,T} \) = fator de correção de exposição para o terreno da cidade com base na Figura NA.8 da BS EN 1991-1-4 Anexo Nacional
Para determinar o fator de exposição, \({c}_{e}(z)\) , para a placa, precisamos calcular o \(z – {h}_{dis}\) e a distância a favor do vento até a costa em km. Pela simplicidade, vamos definir a altura de deslocamento, \({h}_{dis}\), para 0. Para o \(z \) valores, vamos considerá-lo em \(z = 38.0\) e \(z = 44.0\). além disso, a distância a favor do vento até a costa é superior a 100 km. Portanto, usando a Figura NA.7 da BS EN 1991-1-4 Anexo Nacional:
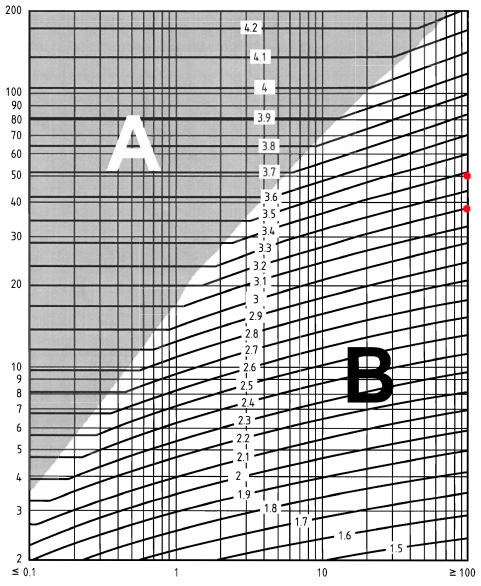
Figura 6. Figura NA.7 da BS EN 1991-1-4 Anexo Nacional.
Portanto:
\({c}_{e}(38.0) = 3.2\)
\({c}_{e}(44.0) = 3.3\)
Por outro lado, o fator de correção de exposição \( {c}_{e,T} \) para a placa pode ser determinado na Figura NA.8 da BS EN 1991-1-4 Anexo Nacional. Usando a distância dentro do terreno da cidade igual a 1km, podemos obter o fator de correção de exposição \( {c}_{e,T} \):
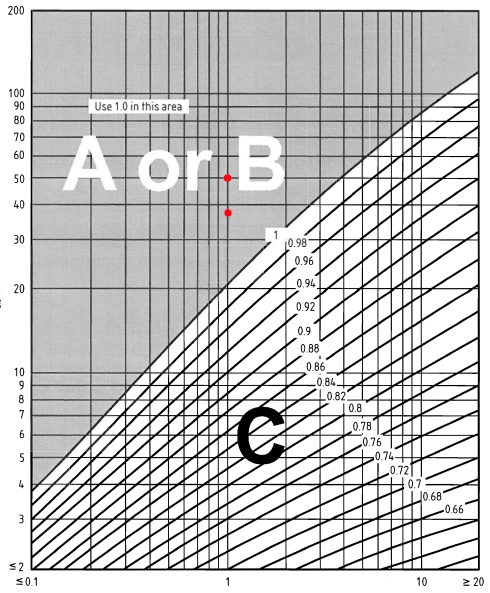
Figura 7. Figura NA.8 da BS EN 1991-1-4 Anexo Nacional.
Portanto:
\({c}_{e,T}(38.0) = 1.0\)
\({c}_{e,T}(44.0) = 1.0\)
Usando os valores acima, podemos calcular a pressão de velocidade de pico, \({q}_{p}(z)\), pra \(z = 38.0\) e \(z = 50.0\):
\({q}_{p}(44.0) = (3.3)(1.0)(353.09) = 1165.20 Nós vamos \)
\({q}_{p}(38.0) = (3.2)(1.0)(353.09) = 1129.89 Nós vamos \)
Fator Estrutural, \( {c}_{s}{c}_{d} \)
Para nossa placa, usaremos o valor simplificado para o fator estrutural, \({c}_{s}{c}_{d}\), ser igual a 1.0 A partir da elevação do solo gerada a partir das elevações do Google 6 ou e 1991-1-4.
Coeficiente de Força, \( {c}_{f}\), para tabuleta
Para placas, o coeficiente de força, \({c}_{f}\), é igual a 1.8 A partir da elevação do solo gerada a partir das elevações do Google 7.4.3 ou e 1991-1-4.
Força do vento, \( {F}_{C,tabuleta} \), agindo na placa
A força que atua na placa pode ser calculada usando a Equação (7) A partir da elevação do solo gerada a partir das elevações do Google 5.3(2) ou e 1991-1-4.
\({F}_{C,tabuleta} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({z}_{e}){A}_{referência,tabuleta} = (1.0)(1.8)(1165.20Nós vamos)(12.0m)(12.0m)\)
\({F}_{C,tabuleta} = 302019.84 N\)
Observe que a excentricidade horizontal desta força do vento que atua no centroide da placa é recomendada como sendo igual a 3,0m.
Os cálculos de vento podem ser realizados usando o SkyCiv Load Generator for EN 1991 (calculadora de carga de vento de placa e poste). s/h, s/h. s/h, você pode agilizar esse processo e obter um relatório detalhado de cálculo de carga de vento para placas e postes!
Força do vento, \( {F}_{C,pólo} \), atuando no poste
similarmente, a força que atua no poste pode ser calculada usando a equação (7) A partir da elevação do solo gerada a partir das elevações do Google 5.3(2) ou e 1991-1-4.
\({F}_{C,pólo} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({z}_{g}){A}_{referência,pólo}\) (8)
Onde:
\({c}_{f} = {c}_{f,0}{ψ}_{λ} \)
\({A}_{referência,pólo} = {z}_{g}d \)
Observação:
\(ψ_{λ} \) é calculado com base na esbeltez efetiva, \( λ \), usando usando Figura 7.36 da seção 7.13 ou e 1991-1-4
\({c}_{f,0}\) é calculado com base no número de Reynolds \( R_{e} \) usando figura 7.28 ou e 1991-1-4
Onde:
\( {z}_{g} \) é a altura do poste ao solo em m
\( d \) é o diâmetro do poste em m
\( ν = 0.000015 m²/s \) é a viscosidade cinemática do ar
\( v({z}_{g}) = (2{q}_{p}({z}_{g})/ρ)^{0.5} \) (9)
\( {R}_{e} = v(z_{g})d / ν \) (10)
Vamos nos aprofundar nesses parâmetros nas próximas seções
Número de Reynolds, \( {R}_{e} \), para o pólo
Usando os valores calculados acima, podemos calcular \( v({z}_{g}) \) usando equação (9):
\( v({z}_{g}) = (2{q}_{p}({z}_{g})/ρ)^{0.5} = (2(1129.89)/(1.226))^{0.5} \)
\( v({z}_{g}) = 42.93 m/s\)
Portanto, o número de Reynolds \( R_{e} \) para o pólo, usando equação (10) é:
\( {R}_{e} = v({z}_{g})d / ν = (42.93)(1.0)/(0.000015) \)
\( {R}_{e} = 2862000 \)
Coeficiente de força, \( {c}_{f0} \), sem fluxo de extremidade livre
O material do poste que usamos é ferro fundido que tem rugosidade da superfície equivalente \( k \) Caso de carga A 0.2 baseado na tabela 7.13 ou e 1991-1-4.
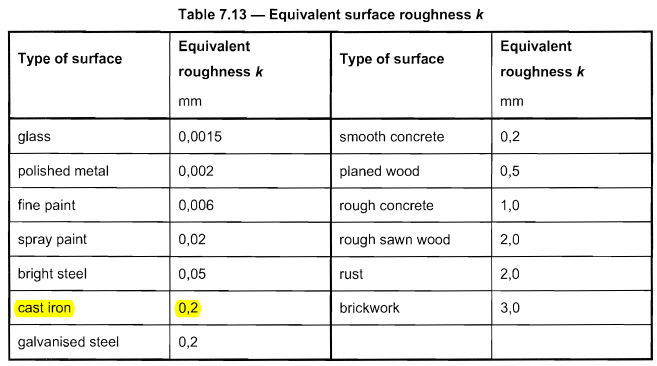
Figura 8. Mesa 7.13 ou e 1991-1-4 para rugosidade equivalente \( k \).
O coeficiente de força \( {c}_{f0} \) pode ser determinado usando a fórmula da Figura 7.28 de PT 1991-1-4 com \( k/d = 0.2\):
\( {c}_{f0}= 1.2 + {0.18registro(10 k/d)}/{1 + 0.4registro({R}_{e}/{10}^{6}} = 1.2 + {0.18registro(10 (0.2)}/{1 + 0.4registro((2862000)/{10}^{6}}\)
\( {c}_{f0} = 1.246 \)
Esbeltez Eficaz, \( λ \)
A magreza efetiva, \( λ \), para o pólo pode ser determinado na Tabela No.4 7.16 ou e 1991-1-4.
\( λ = máx.(0.7 {z}_{g}/d, 70) \) pra \( {z}_{g} \) > 50m
\( λ = máx.({z}_{g}/d, 70) \) pra \( {z}_{g} \) < 15m
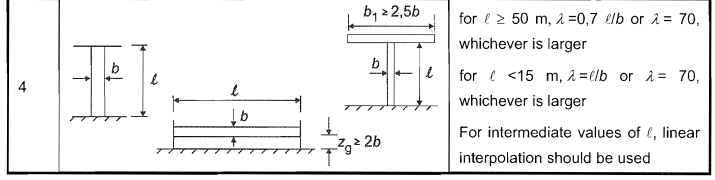
Figura 9. Mesa 7.16 ou e 1991-1-4 para calcular a esbeltez efetiva \( λ \).
Desde a \( {z}_{g} \) é igual a 38,0m, precisamos interpolar os valores de \( λ \) para 50m e 15m:
\( {z}_{g} = 38\)
\( {λ}_{50m} = máximo(0.7 (38), 70) = 70 \)
\( {λ}_{15m} = máximo((38), 70) = 70 \)
Portanto:
\( λ = 70 \)
Fator de efeito final, \( {ψ}_{λ} \)
O fator de efeito final, \( {ψ}_{λ} \), pode ser obtido usando a Figura 7.36 ou e 1991-1-4 exigindo a relação de solidez \( Phi \) e magreza efetiva \( λ \). Vamos assumir a razão de solidez \( Phi \) Caso de carga A 1.0 uma vez que a coluna do tubo não tem nenhuma perfuração.
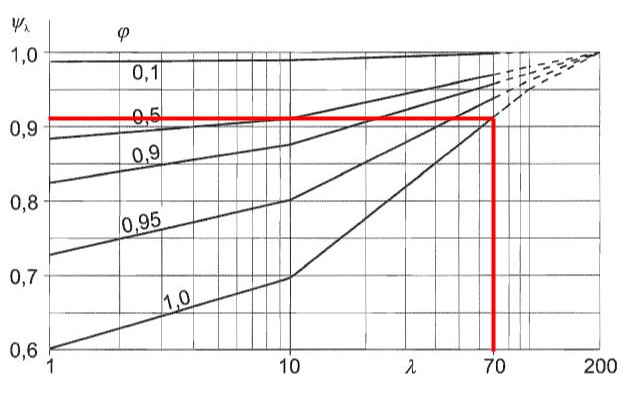
Figura 10. O fator de efeito final correspondente \( {ψ}_{λ} \) para o poste que suporta a placa com base na Figura 7.36 ou e 1991-1-4.
Da Figura 10, podemos deduzir que o fator de efeito final \( {ψ}_{λ} \) pois o pólo é igual a 0.910.
A partir dos parâmetros calculados acima,já podemos calcular Força do vento, \( {F}_{C,pólo} \):
\({c}_{f} = {c}_{f,0}{ψ}_{λ} = (1.246)(0.910) = 1.134\)
\({F}_{C,pólo} = {c}_{s}{c}_{d}{c}_{f}{q}_{p}({z}_{e}){A}_{referência,pólo} = (1.0)(1.134)(1129.89)(38.0×1.0) \)
\({F}_{C,pólo} = 48689.22 N \)
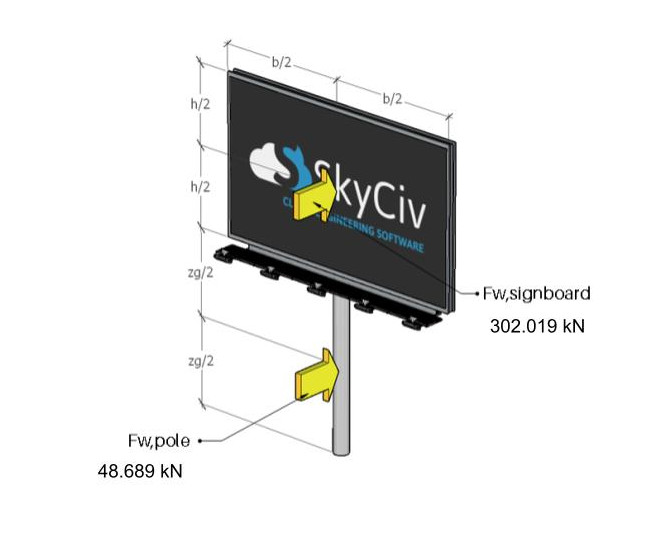
Figura 11. As forças do vento que atuam na placa e no poste.
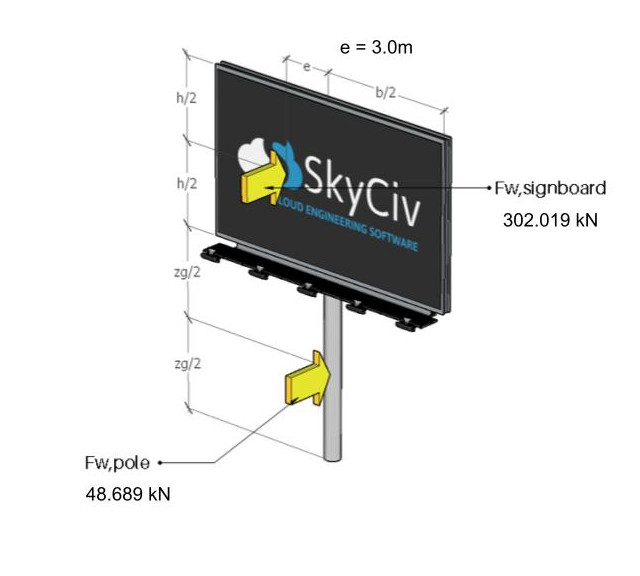
Figura 12. As forças do vento atuando na placa e poste para caixa excêntrica.
SkyCiv Load Generator
Usando o gerador de carga SkyCiv, você pode obter cargas de vento para placas e postes com apenas alguns cliques e entradas. você pode obter cargas de vento e neve em painéis solares montados no solo com apenas alguns cliques e entradas, você poderá gerar o relatório detalhado do vento para o seu projeto de letreiro!
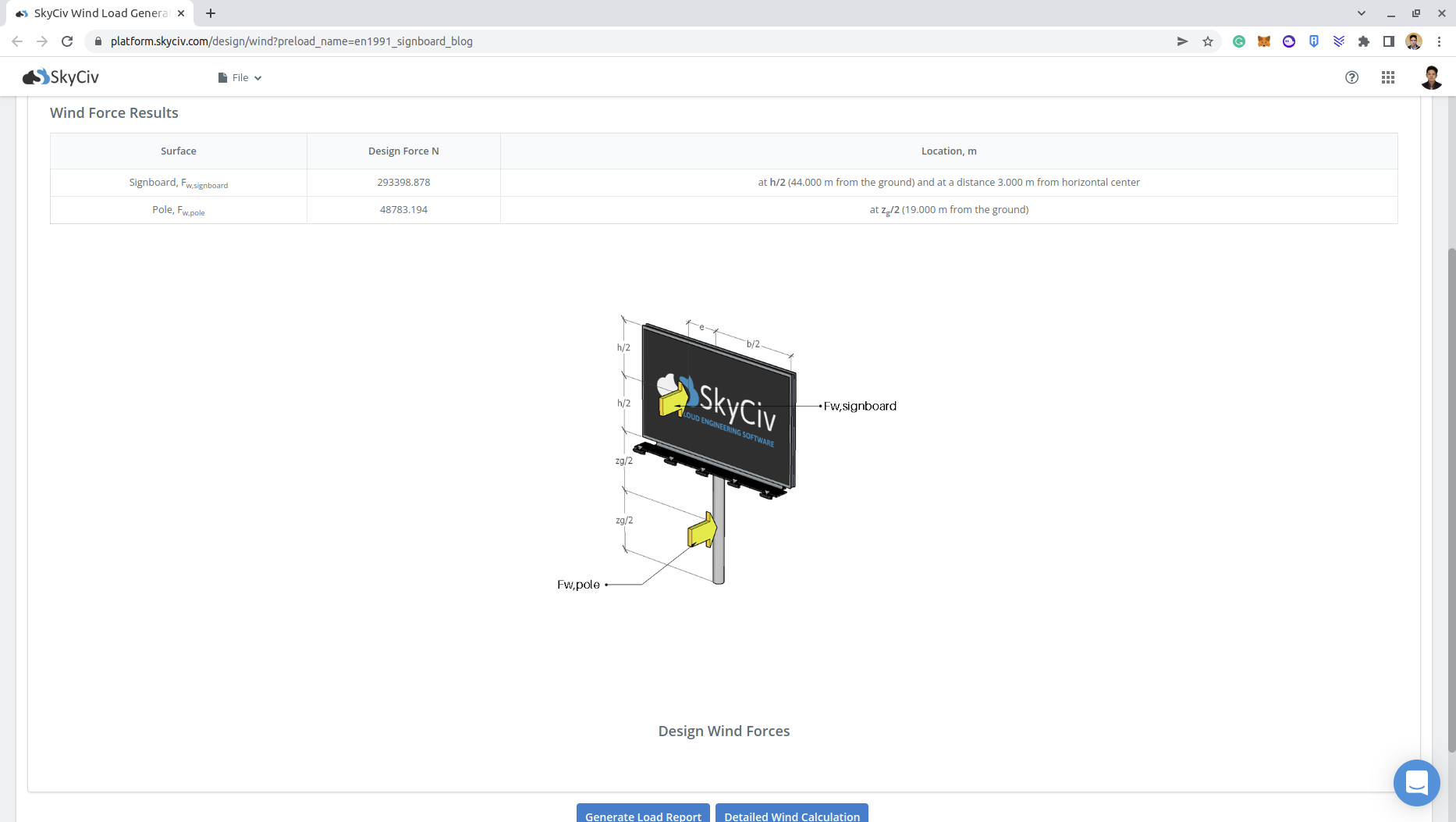
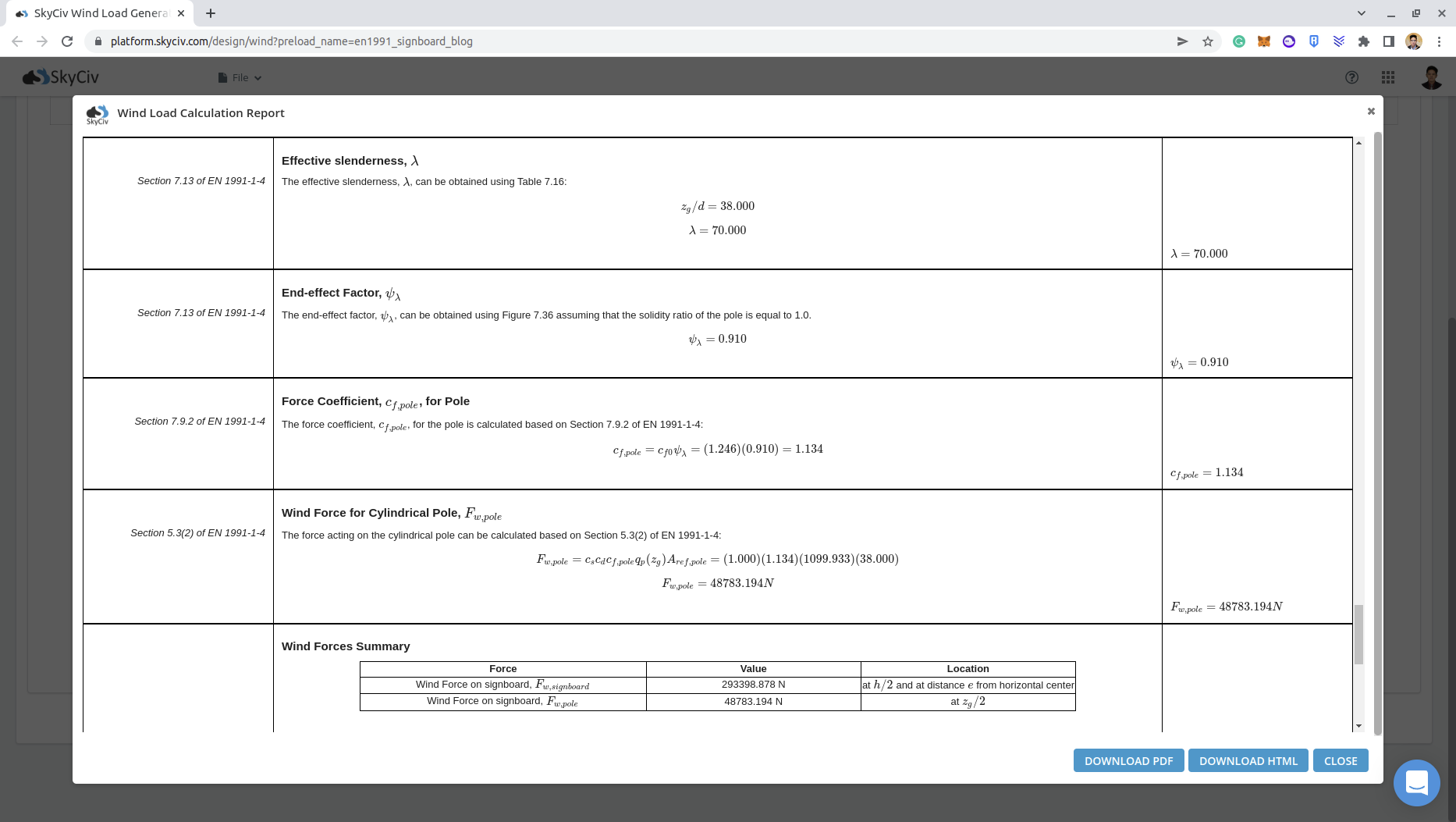
Você pode verificar o relatório detalhado de carga de vento para a placa de sinalização através desses links:
Engenheiro estrutural, Desenvolvimento de Produto
MS Engenharia Civil
Referências:
- Sobre, B. (2005). Eurocódigo 1: Ações em Estruturas - Parte 1-4: Ações Gerais - Ações do Vento.
- BSI. (2005). BS EN 1991-1-4: 2005+ A1: 2010: Eurocódigo 1. Ações em estruturas. Ações gerais. Ações do vento.


