O momento de inércia é uma importante propriedade geométrica usada na engenharia estrutural.. Está diretamente relacionado à quantidade de resistência do material que sua seção possui.. Geralmente, um maior momento de inércia implica uma maior resistência na seção, resultando em deflexão reduzida quando submetido a uma carga. O momento de inércia de um retângulo, Uma análise detalhada, é tecnicamente uma medida de quanto torque é necessário para acelerar a massa em torno de um eixo – Uma análise detalhada Uma análise detalhada Uma análise detalhada.

Fórmula do Momento de Inércia de um Retângulo

A fórmula geral usada para determinar como encontrar o momento de inércia de um retângulo é:

[matemática] Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia{As unidades têm comprimento elevado à potência de}[object Window]{BD^3}{12} , Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia{As unidades têm comprimento elevado à potência de}[object Window]{B^3D}{12} [matemática]

Onde o As unidades têm comprimento elevado à potência de e As unidades têm comprimento elevado à potência de referir-se ao eixo particular, ou direção, sendo considerado.

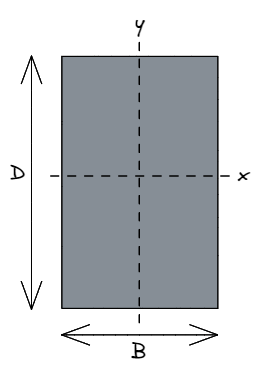
É uma convenção comum de engenharia estrutural que B refere-se a largura do retângulo, paralelo a um convencionalmente horizontal eixo x.

similarmente, D refere-se a profundidade do retângulo, paralelo a um convencionalmente vertical eixo y.

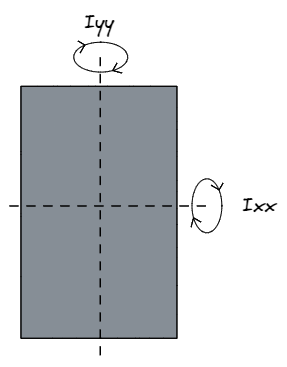
Pode ser confuso no começo, mas quando os engenheiros estruturais se referem a Ixx eles estão de fato referenciando a força de uma seção sobre o eixo x, ou seja, em uma direção paralela ao D dimensão, ou eixo y. similarmente, aaaa refere-se à força sobre o eixo y, ou seja, em uma direção paralela ao B dimensão, ou eixo x.

Seções Ocas Retangulares (RHS)

Embora os engenheiros possam hipoteticamente usar seções retangulares sólidas ao projetar, isso usaria uma quantidade significativamente maior de matéria-prima, com aumentos correspondentes em peso e custo. É muito mais comum usar retângulos seções ocas (comumente referido como um RHS). Aqui podemos utilizar a mesma equação definida acima para o caso retangular geral, Contudo, devemos subtrair o interior oco área do retângulo:

[matemática] Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia{As unidades têm comprimento elevado à potência de}[object Window]{BD^3}{12} – \dfrac{bd^3}{12} [matemática]

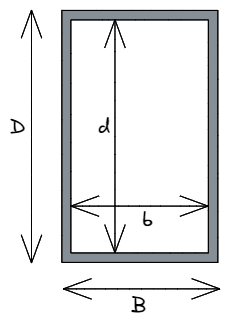
Neste caso, minúsculas b e d denotar o tamanho da área oca dentro do retângulo que devemos subtrair das dimensões externas da forma, sendo maiúsculas B e D. A diferença entre cada dimensão correspondente refere-se à espessura do material naquela dimensão – ou seja. B – b = espessura total do material paralelo ao eixo x.

Além dos exemplos claros de peso e uso de materiais, por que as seções ocas são frequentemente descritas como mais eficiente do que suas contrapartes sólidas?

Considere uma viga submetida a uma carga vertical para baixo. Esperamos que as fibras superiores do material sofram uma força compressiva, enquanto as fibras inferiores correspondentes sofrerão uma força de tração. As fibras ao longo do eixo neutro da seção (paralelo ao centróide da seção) Contudo, não experimentará compressão nem tensão, daí o nome neutro eixo.

importante, a magnitude dessas forças de compressão ou tração dependem da distância deste eixo neutro – material mais perto ao eixo neutro precisa resistir menos força.

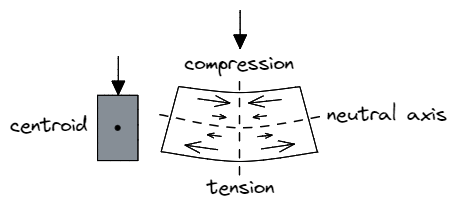
Assim sendo, o material interno de uma seção totalmente sólida está resistindo a uma quantidade relativamente pequena de força enquanto ocupa uma área relativamente grande porque o material mais externo está trabalhando mais! Retirar essa parte interna da seção e torná-la oca melhora consequentemente a eficiência da seção em relação ao seu peso, custo, e uso de materiais.

Conclusão

Resumindo, a fórmula para determinar o momento de inércia de um retângulo é Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. Para seções ocas retangulares, a fórmula é Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

O momento de inércia é importante tanto para a força/tensão do momento fletor quanto para a deflexão. Isso é evidente em suas fórmulas, como em ambos os casos, eu (Momento de inércia) Uma análise detalhada:

Fonte: Fórmula de Flexão de Tensão

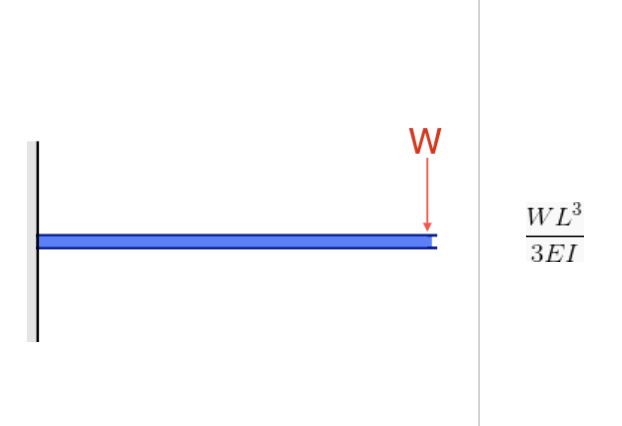
Fonte: Equação de deflexão em uma viga em balanço

Calculadora do Momento de Inércia de um Círculo

Se você deseja calcular o momento de inércia, confira nosso tutorial sobre o Momento de Inércia de um Círculo para ver como as formas de seção circulares e retangulares se comparam entre si.

Calculadora de momento de inércia grátis