Os Fundamentos do Centroide
É importante notar que em um corte transversal, cuja área é uniforme em todo, o centroide pode ser encontrado tomando a soma dos momentos em relação a um eixo definido arbitrariamente, mas geralmente é definido na fibra superior ou inferior. Confira nosso artigo anterior sobre como encontrar o centróide de uma seção de feixe e SkyCiv Free Centroid Calculator.
Fundamentalmente, o centroide pode ser obtido tomando a soma dos momentos sobre a soma da área. Que se expressa assim.
[math]
\bar{x}= frac{1}{A}\int xfesquerda ( xdireita )dx
[math]

Resumo das Equações Centróides
Na equação acima, f(x) é a função e x é o braço do momento. Para ilustrar melhor isso, derivaremos o centróide y de um triângulo arbitrário com sua base coincidente com o eixo x. Nesta situação, a forma do triângulo, se é equilátero, isósceles ou escaleno é irrelevante, pois tudo é relativo apenas ao eixo x. Observe que a forma é irrelevante se a base do triângulo for coincidente ou paralela em relação ao eixo. Este não será o caso ao resolver para o centróide x. Em vez de, você pode imaginá-lo como obtendo o centróide de dois triângulos retângulos em relação ao eixo y. Por conveniência, vamos imaginar um triângulo isósceles semelhante à tabela de referência abaixo. Encontrar a relação entre b e h resultará na seguinte relação.
[math]
\fratura{-Y}{x}= frac{-h}{b}
[math]
Observe que a inclinação é negativa, pois estamos imaginando o triângulo na vertical. Se imaginarmos o triângulo invertido, a inclinação seria positiva. Independentemente, a relação continua a mesma. Como x = f(Y), a relação acima pode ser reescrita como a seguir.
[math]
x=fesquerda ( y direita )= frac{b}{h}Y
[math]
Agora podemos resolver para o centroide. Ajustando a primeira equação acima, obtemos o seguinte.
[math]
\bar{Y}= frac{1}{A}\int yfesquerda ( y direita )dy
[math]
Conectando valores adicionais e substituindo a relação acima resultará na seguinte equação.
[math]
\bar{Y}= frac{2}{bh}\int_{0}^{h} \fratura{b}{h}Fundamentos do Momento de Inércia{2}dy
[math]
Simplificando,
[math]
\bar{Y}= frac{2}{Fundamentos do Momento de Inércia{2}}\deixou [ \fratura{Fundamentos do Momento de Inércia{3}}{3} \direito ]_{0}^{h}
[math]
[math]
\bar{Y}= frac{2}{Fundamentos do Momento de Inércia{2}}\deixou [ \fratura{Fundamentos do Momento de Inércia{3}}{3}-0 \direito ]
[math]
[math]
\bar{Y}= frac{2}{3}h
[math]
Observe que esta solução é tirada do topo. O centróide retirado de baixo deve então ser igual a 1/3 de h.
Fórmula para centróides de formas comuns e seções de feixe
Abaixo está uma lista de um variedade de formas de seção de viga e a distância aos centróides da seção. As equações mostram como encontrar o centroide de uma seção específica a partir da base ou do ponto mais à esquerda da seção. Para assinaturas SkyCiv Student e Structural, esta referência também pode ser baixada como uma referência em PDF para levar com você onde quer que vá. Os centróides de uma seção de viga são extremamente importantes, pois localizam o eixo neutro e são uma das primeiras etapas necessárias ao analisar uma seção de viga.
SkyCiv também oferece uma Tabela de Resumo de Seções abrangente que contém todas as equações e fórmulas relacionadas às seções de vigas (momento de inércia, área etc…).
A equação para vários centróides estão listados abaixo:
| As unidades têm comprimento elevado à potência de | CY (Distância de baixo) |
Cx (Distância do ponto mais à esquerda) |
Centroide de Retângulo ou Seções Retangulares |
||
|---|---|---|
 |
[math] \dfrac{h}{2} [math] |
[math] \dfrac{b}{2} [math] |
Centroide de uma seção retangular oca |
||
 |
[math] \dfrac{b}{2} [math] |
[math] \dfrac{h}{2} [math] |
Centroide de um círculo ou seção circular |
||
 |
[math] \dfrac{D}{2} [math] |
[math] \dfrac{D}{2} [math] |
Equação Centroide de uma Seção Circular Oca |
||
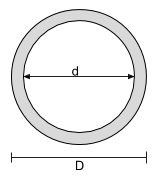 |
[math] \dfrac{D}{2} [math] |
[math] \dfrac{D}{2} [math] |
Centróide de um triângulo isósceles |
||
 |
[math] \dfrac{h}{3} [math] |
[math] \dfrac{b}{2} [math] |
Centróide de um feixe I |
||
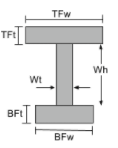 |
[math] \fratura{[object Window] ( BFt + Wh + \fratura{TFt}{2} \direito )}{TFwvezes TFt + Wtvezes Wh + BFwvezes BFt} + [math] [math] \fratura{[object Window] ( BFt + \fratura{Wh}{2} \direito )}{TFwvezes TFt + Wtvezes Wh + BFwvezes BFt} + [math] [math] \fratura{[object Window] ( \fratura{BFt}{2} \direito )}{TFwvezes TFt + Wtvezes Wh + BFwvezes BFt} [math] |
[math] TFw > BFw, \fratura{TFw}{2}[math] [math] BFw > TFw, \fratura{BFw}{2} [math] |
Centroide de uma seção em T |
||
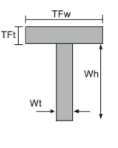 |
[math] \fratura{[object Window] ( \fratura{Wh}{2} \direito )}{TFwvezes TFt + Wtvezes Wh } + [math] [math] \fratura{[object Window] ( Wh + \fratura{TFt}{2} \direito ) }{TFwvezes TFt + Wtvezes Wh } [math] |
[math] \fratura{TFw}{2} [math] |
Centroide de uma cesariana |
||
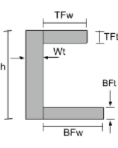 |
[math] \fratura{[object Window] ( h – \fratura{TFt}{2} \direito )}{TFwvezes TFt + Wtvezes Wh + BFwvezes BFt} + [math] [math] \fratura{Wtvezes hvezes esquerda ( \fratura{h}{2} \direito )}{TFwvezes TFt + Wtvezes Wh + BFwvezes BFt} + [math] [math] \fratura{[object Window] ( \fratura{BFt}{2} \direito )}{TFwvezes TFt + Wtvezes Wh + BFwvezes BFt} [math] |
[math] \fratura{TFttimes TFwtimes left ( Em peso + \fratura{TFw}{2} \direito )}{TFtvezes TFw + hvezes Peso + BFtvezes BFw} + [math] [math] \fratura{hvezes Wtvezes esquerda ( \fratura{Em peso}{2} \direito )}{TFtvezes TFw + hvezes Peso + BFtvezes BFw} + [math] [math] \fratura{[object Window] ( Em peso + \fratura{BFw}{2} \direito )}{TFtvezes TFw + hvezes Peso + BFtvezes BFw} [math] |
Centróide de um ângulos |
||
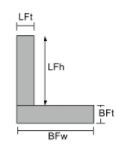 |
[math] \fratura{LFttimes LFhtimes left ( BFt + \fratura{LFh}{2} \direito ) }{LFtvezes LFh + BFwvezes BFt} + [math] [math] \fratura{[object Window] ( \fratura{BFt}{2} \direito )}{LFtvezes LFh + BFwvezes BFt} [math] |
[math] \fratura{LFhtimes LFttimes left ( \fratura{LFt}{2} \direito )}{LFhvezes LFt + BFtvezes BFw} + [math] [math] \fratura{[object Window] ( \fratura{BFw}{2} \direito )}{LFhvezes LFt + BFtvezes BFw} [math] |
Equações automáticas para centróide do feixe
Confira nosso Calculadora Centroide Gratuita, uma versão simplificada de SkyCiv Section Builder, calcular o centróide do feixe automaticamente, sem necessidade de cálculos manuais. Ou inscreva-se hoje para começar!


