Descrição geral
SkyCiv incluiu um novo recurso poderoso que consiste na análise do espectro de resposta da placa na plataforma. Neste artigo, vamos cobrir um exemplo de um pequeno edifício, como mostra a imagem a seguir. O objetivo principal é explicar alguns detalhes essenciais ao executar uma análise semelhante por conta própria.
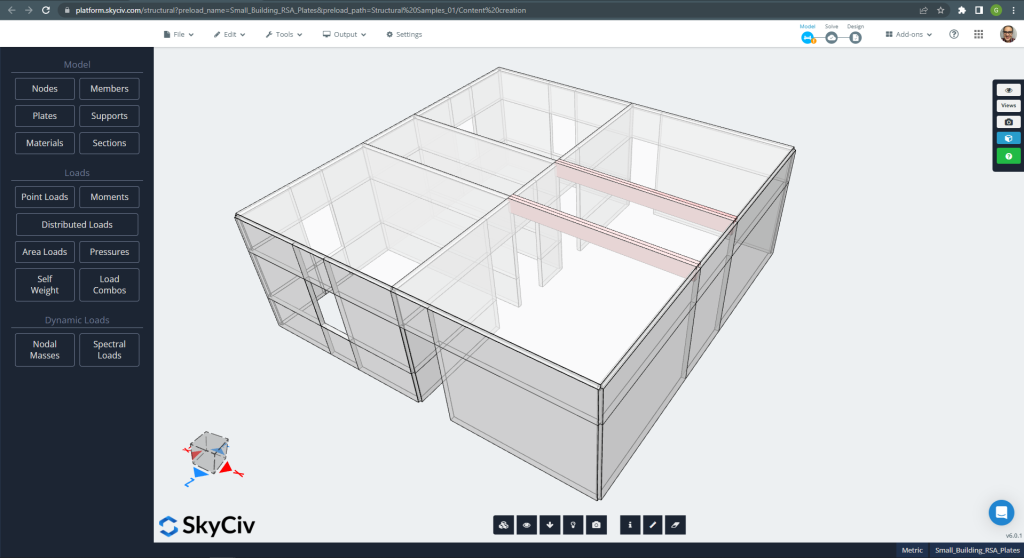
Figura 1. Exemplo de Edifício Pequeno
Você pode ver que a pequena estrutura de concreto armado possui paredes e lajes construídas com o elemento de placa SkyCiv. Ao projetar o edifício para cargas dinâmicas, como terremotos, a maioria dos códigos de construção estabelece alguns métodos, como o 'Procedimento ou Análise de Espectro de Resposta (RSA).’
O RSA consiste em tomar a aceleração do nível de projeto sísmico através de uma curva suave dada pelo código. Você pode ler estes artigos SkyCiv: Análise de espectro de resposta: Um exemplo de construção e análise de espectro de resposta: Métodos de combinação modal para mais informações e exemplos Análise de espectro de resposta: Exemplos de construção e Análise de espectro de resposta: Métodos de Combinação Modal.
Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!
Modelo de elementos finitos: Análise Dinâmica de Placas
Depois que a geometria e os materiais do exemplo forem definidos, o próximo passo crucial é executar uma análise linear de uma estrutura em malha. Por favor, dê uma olhada no modelo na Figura 2.
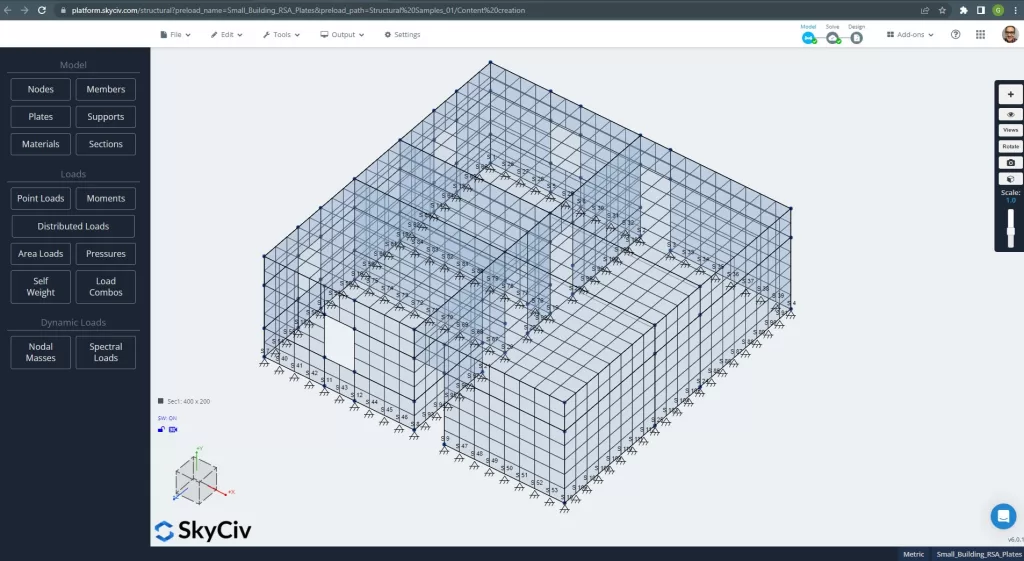
Figura 2. Edifício pequeno em malha
A equação de movimento a ser resolvida ao executar uma análise de espectro de resposta tem a forma de:
\({Meu}{\ponto{X_e}}+{C_e}{\ponto{X_e}}+{K_e}{X_e}={-\ponto{X_0}{(t)}{Meu}{J}}\)
Onde:
- \({Meu}\) é a matriz consistente para massas.
- \({C_e}\) é a matriz de amortecimento (Muitas vezes, este valor pode ser calculado como a combinação linear das matrizes de rigidez e massa \({C_e}={\alfa}{K_e}+{\beta}{M}\) ).
- \({K_e}\) é a matriz de rigidez.
- \({X_e}\) é o vetor de deslocamento em relação à base da estrutura.
- \({X_0}{(t)}\) é o vetor de deslocamento do solo (Tem todos os graus de liberdade: 3 deslocamentos e três rotações).
- \({J}\) é um vetor com componentes unitários.
Due SkyCiv usando o método de elementos finitos para placas, o Matrix \({Meu}\) poderia ser obtido através da seguinte expressão para Energia Cinética:
\({E_c}={\fratura{1}{2}}{\int_{volume} {\rho}{\ponto{x}^ 2}{dw}Vol}\) .
Escrevemos agora o \(x\) deslocamento em função de seus nós e usar algumas expressões de interpolação (\(N_{x}^{T}\)).
\({x}=N_{x}^{T} {x}\). Se inserirmos esse valor na equação de energia, logo temos:
\({E_c}={\fratura{1}{2}}{\ponto{x}^{T}}\{{\int_{volume}{\rho}{N}{N^T}{d}{Vol}}\} \ponto{x} \)
Então, Nós podemos dizer que:
\( M = {\int_{volume}{\rho}{N}{N^T}{d}{Vol}}\)
Definir a matriz acima nos permite executar uma análise modal, que é necessário para a análise dinâmica. Figura 3 nos ajuda com algumas informações recomendadas.
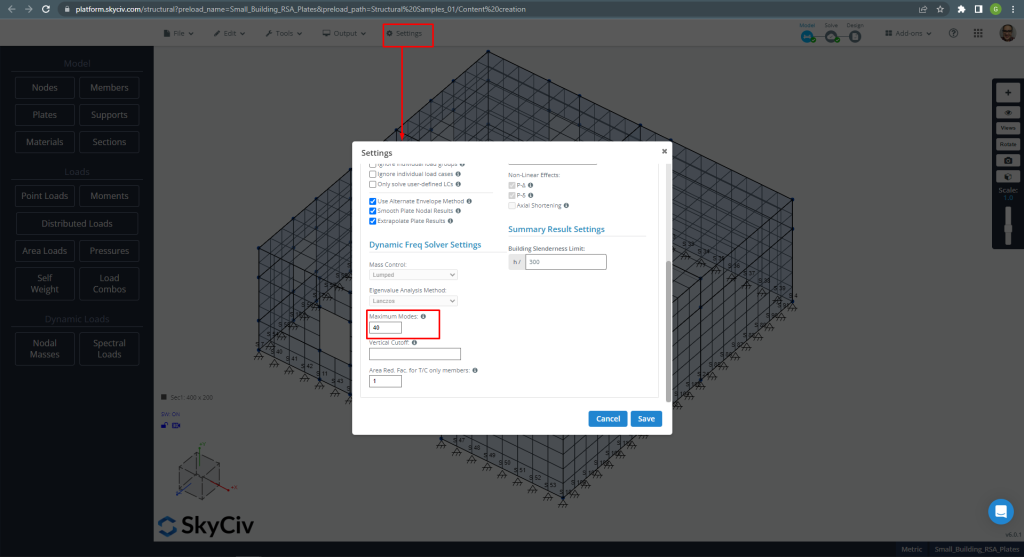
Figura 3. Modos máximos considerados aumentados até 40
Recomenda-se aumentar o número total de modos até cumprir rigorosamente os códigos. Isso afetará os fatores totais de participação em massa, que devem atingir um valor de 90%.
Aplicando Cargas Sísmicas
O próximo passo é definir as cargas espectrais. Podemos incluir uma função customizada ou pegar os cases previamente construídos pela plataforma SkyCiv. Este exemplo usa para cada direção principal do plano de construção um gráfico ASCE. Verifique as entradas na Figura 4 e figura 5.
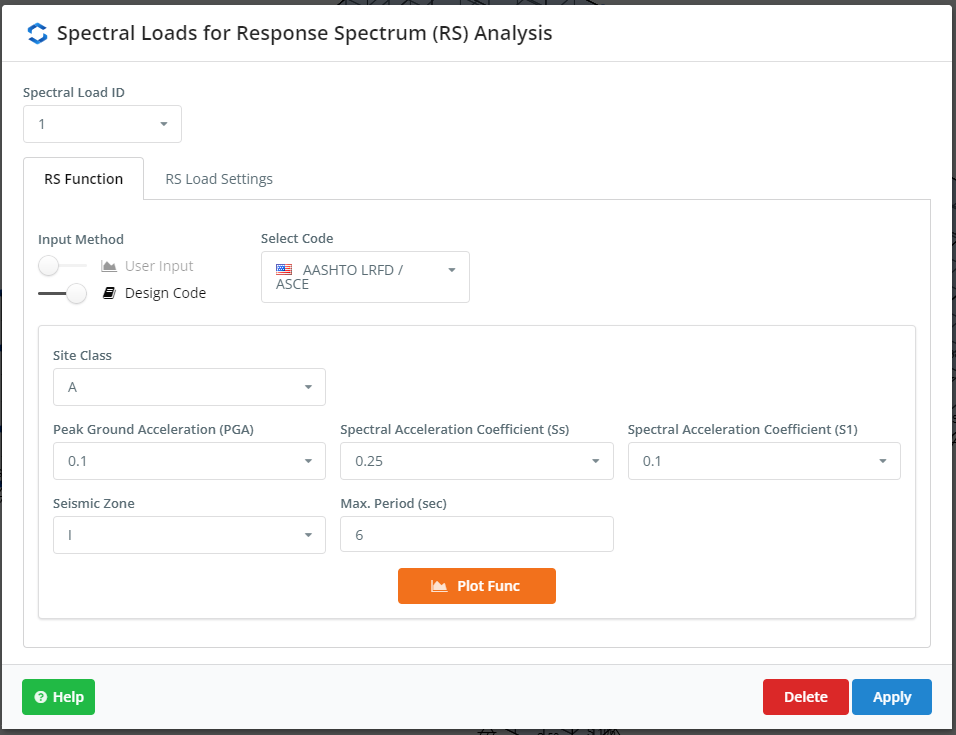
Figura 4. Configurações para RSA, parte um
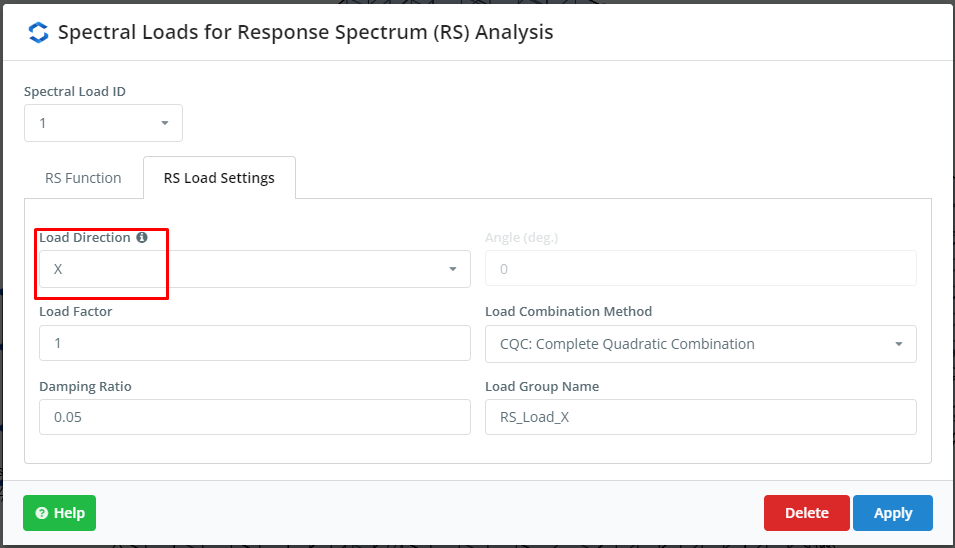
Figura 5. Configurações para RSA, parte dois
Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!
Análise de resultados e conclusões
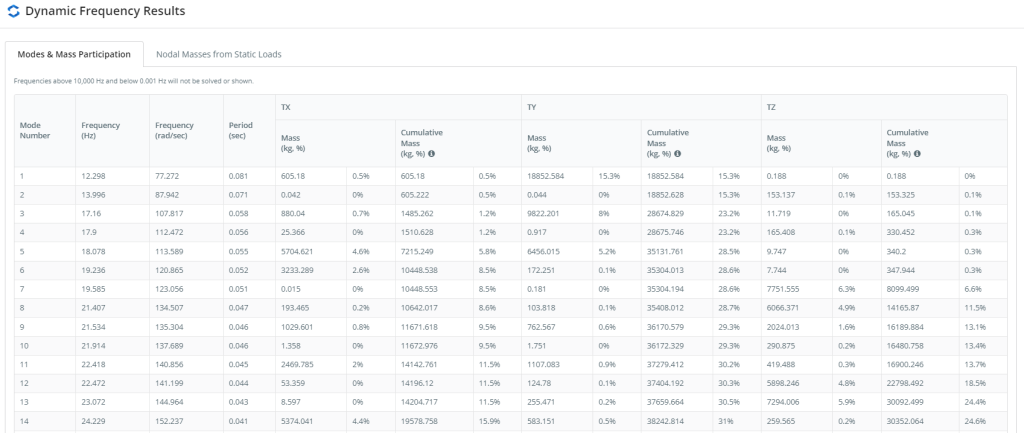
Figura 6. Modos e Resumo de Participação em Massa, parte um
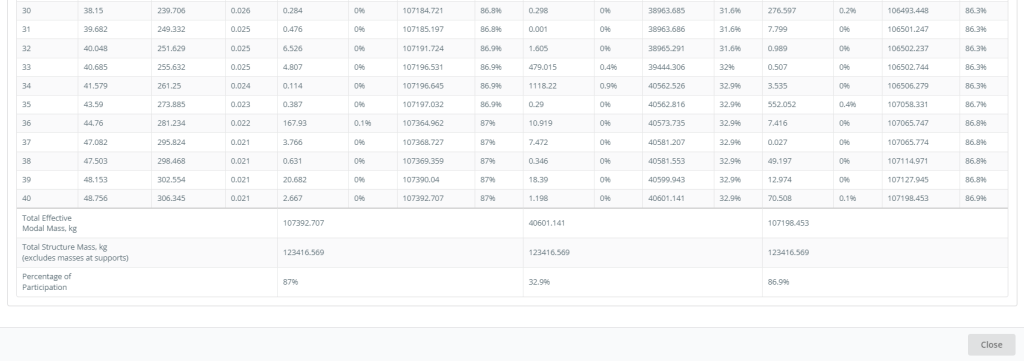
Figura 7. Modos e Resumo de Participação em Massa, parte um
Figuras 6 e 7 dê os modos e valores de participação em massa. Estas tabelas definem os principais modos em cada direção do plano correspondentes àqueles com maiores valores de participação em massa.
Modo 24, T = 0.029 segundos, participação em massa = 44.80 % 'direção x':
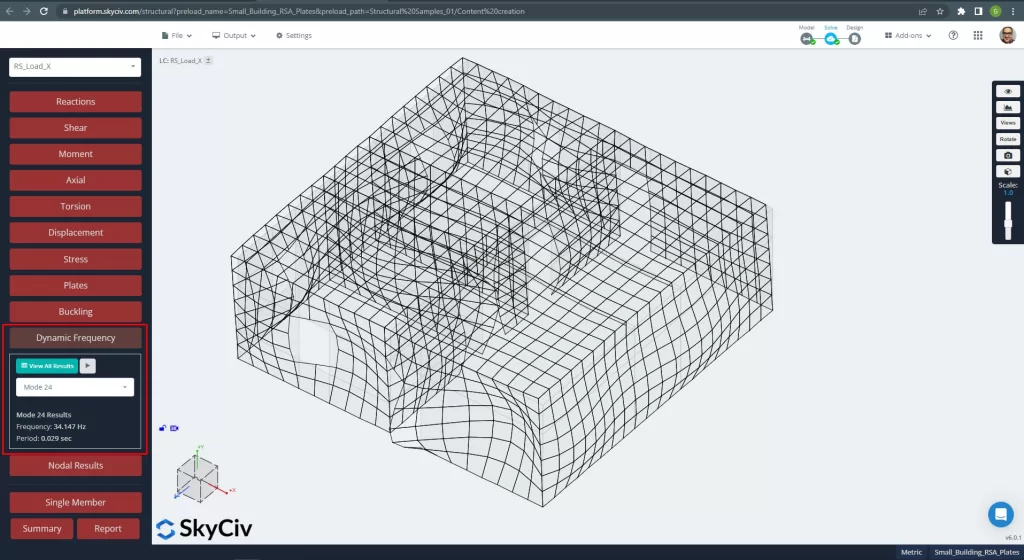
Figura 8. Modo modal principal para direção X.
Modo 23, T = 0.030 segundos, participação em massa = 41.80 % 'direção z':
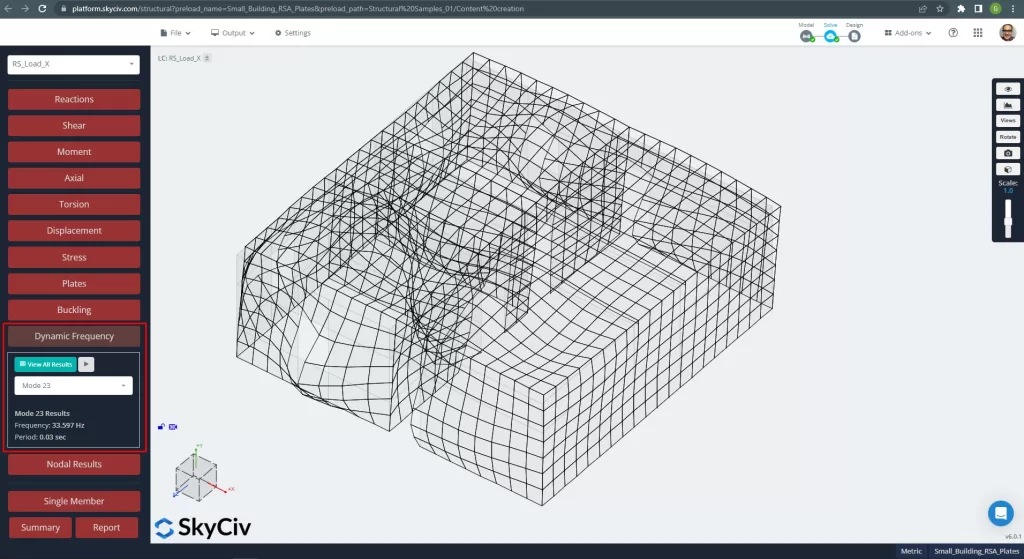
Figura 9. Modo modal principal para direção Z.
SkyCiv também fornece os deslocamentos, forças, esforços, e assim por diante ao executar o RSA. As imagens a seguir nos ajudam a entender como os edifícios se comportam.
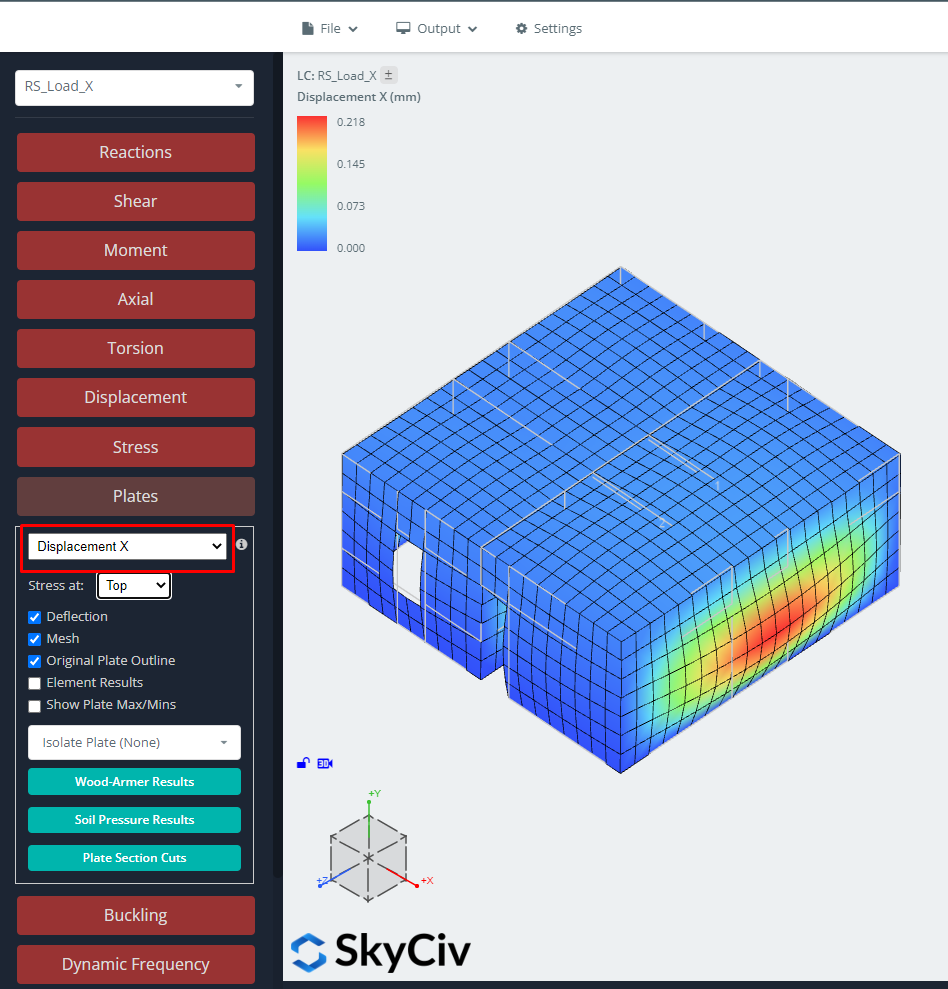
Figura 10. Deslocamentos na direção X para caso de carga RSA.
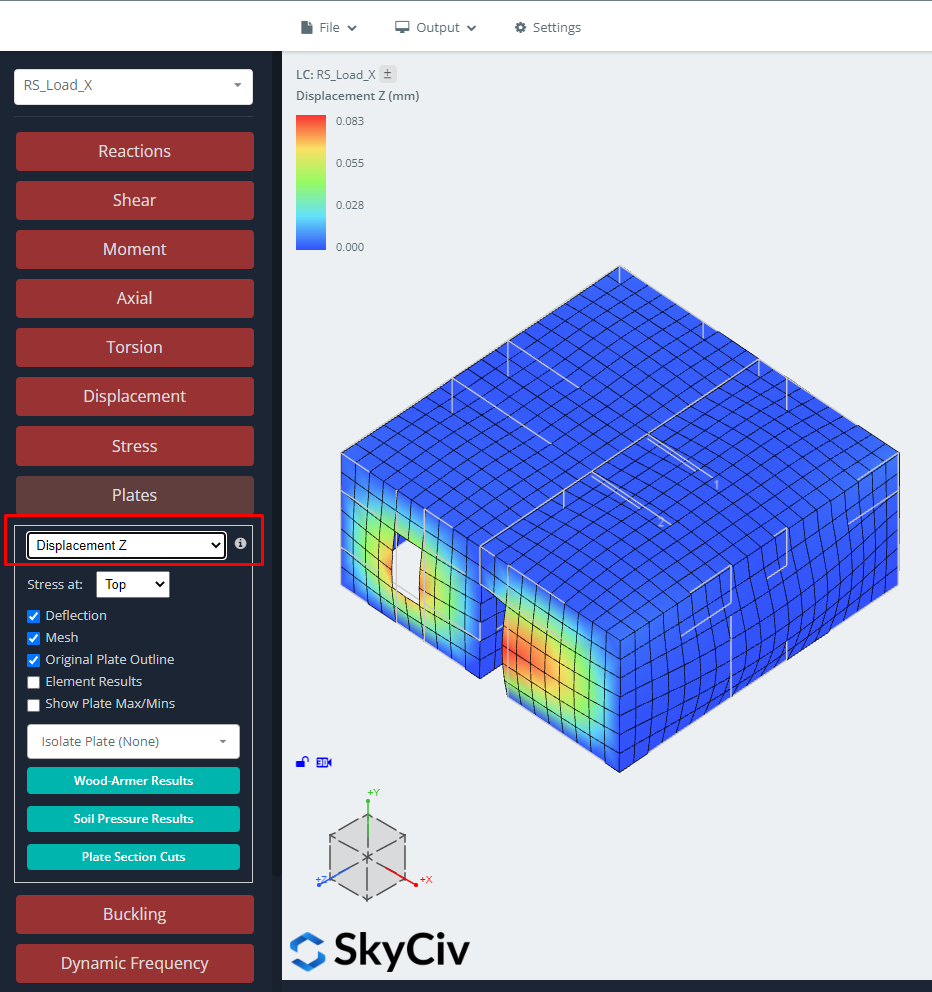
Figura 11. Deslocamento na direção Z para caso de carga RSA.
Agora você pode projetar os elementos da placa com esses resultados. Sugerimos que você leia os artigos SkyCiv sobre Plate Design: Módulo de Design de Placa e exemplos de placas baseadas em código aplicados nos links a seguir: ACI, AS-3600 e Eurocódigo 2.
Além disso, com SkyCiv, podemos obter as reações básicas para o projeto da fundação.
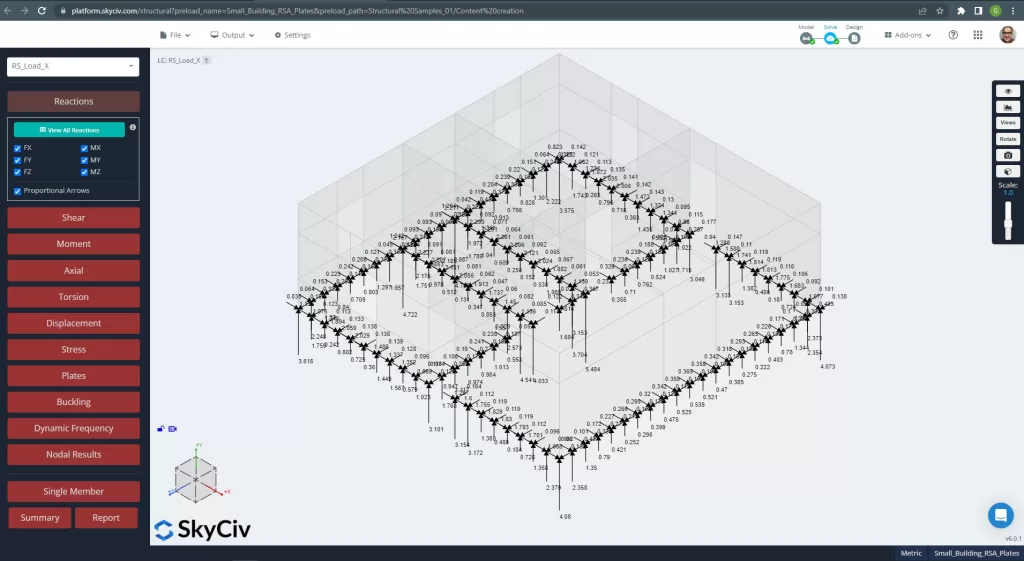
Figura 12. Reações básicas para caso de carga RSA.
Apenas esteja ciente dos sinais de resultados! Todos eles vieram em valores positivos ou absolutos. Isso ocorre porque obtemos os valores absolutos máximos para cada componente de design ao usar um método RSA.
Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!

