Exemplo de cálculo do momento de capotamento – Como Calcular o Fator de Segurança Contra Deslizamento para Muro de Contenção
Este é um guia simples sobre como calcular o momento de tombamento em um muro de arrimo com exemplos. A primeira verificação de estabilidade realizada para um Muro de Contenção de Concreto Cantilever é contra tombamento. Refere-se à capacidade das forças resistentes de impedir que a parede gire em relação ao canto inferior esquerdo da base para a ação das forças de tombamento. Esses dois grupos de carga (resistindo e derrubando) são divididos da seguinte forma:
Resistência a cargas:
- Peso próprio da parede de retenção
- Solo ativo sobre o peso do calcanhar
- Sobretaxa de carga
Cargas tombadas:
- Pressão lateral ativa do solo
- Pressão lateral que resulta da presença da sobrecarga
Dito isto, a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga:
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga:
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga
- Altura: 3.124 m
- Largura: 0.305 m
- Desvio: 0.686 m
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga
- Largura: 2.210 m
- Espessura: 0.381 m
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga
- a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: 18.85 kN / m3
- o ângulo de atrito: 35 graus
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga
- a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: 18.85 kN / m3
- o ângulo de atrito: 35 graus
- a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: 0.55
- a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: 143.641 kPa
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga:
- a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: 3.505 m
- passivo: 0.975 m
- a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: 0.792 m
a força de atrito que impedirá o deslizamento da parede é a carga vertical total multiplicada pelo coeficiente de atrito solo-concreto definido para o material do solo da subestrutura e a força de deslizamento é o resultado da pressão lateral do solo retido e da pressão associada à presença da sobrecarga: -17.237 kN / m
Cargas verticais:
Todas as cargas verticais a que o muro de arrimo cantilever de concreto está submetido são mostrados na figura a seguir:
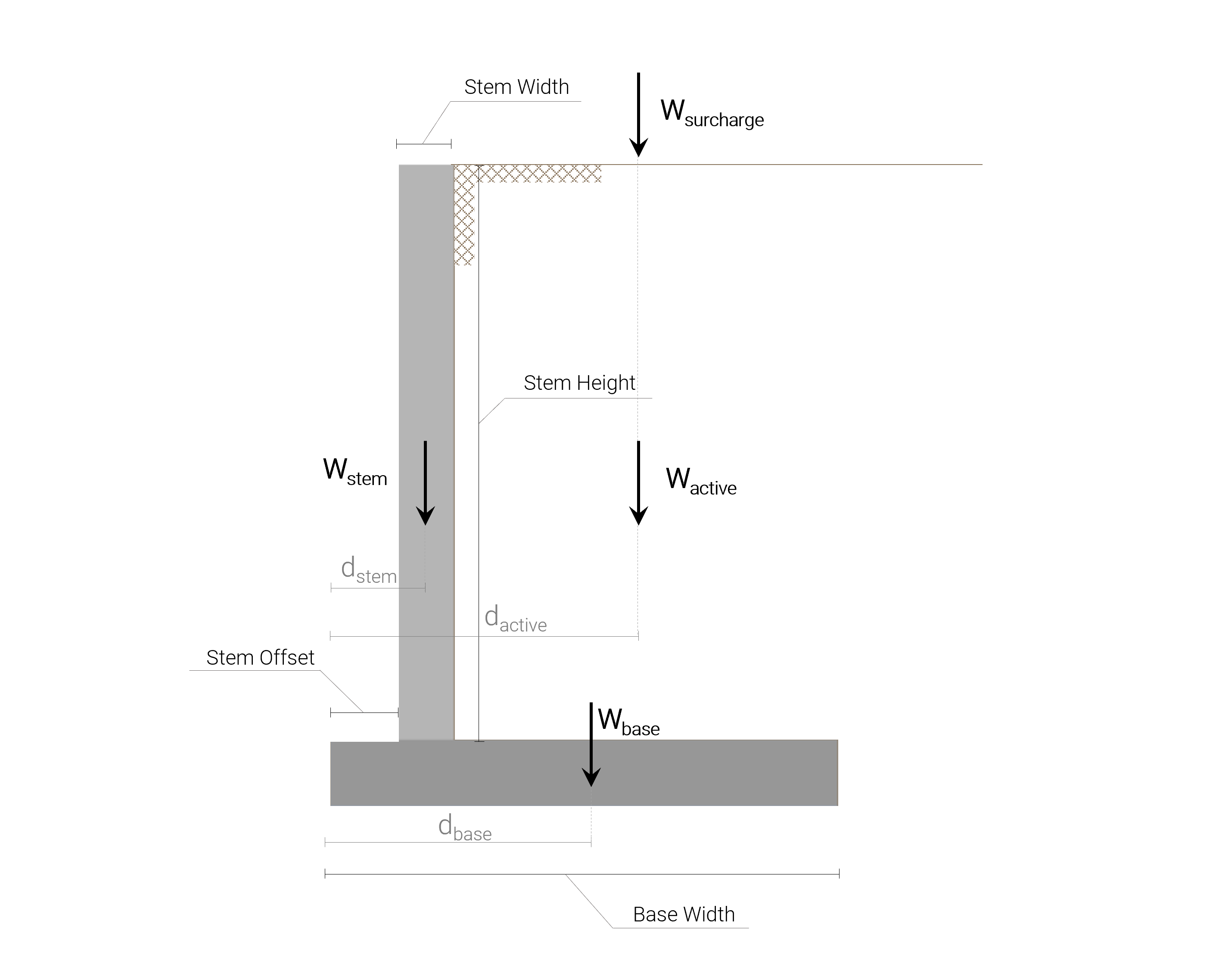
Vale a pena mencionar aqui, que o peso (carga vertical) e o momento associado à porção de solo passivo são desprezados, pois pode ser removido ou erodido e é uma suposição conservadora.
\(W_{stem} = \gamma_{concrete} \cdot (stem_{height} \cdot stem_{width} ) = 23.58 kN/m^3 \cdot 3.124m \cdot 0.305m\)
\( W_{stem}= 22.467kN/m\)
\(W_{base} = \gamma_{concrete} \cdot (base_{thickness} \cdot base_{width} ) = 23.58 kN/m^3 \cdot 0.381m \cdot 2.210m\)
\( W_{base}= 18.855 kN/m\)
\(W_{active} = \gamma_{soil,active} \cdot (stem_{height}\cdot (base_{width}-stem_{offset}-stem_{width}) ) \)
\( W_{active} = 18.85 kN/m^3 \cdot 3.124m \cdot (2.210-0.686-0.305)m\)
\( W_{active} = 71.784 kN/m\)
\(W_{surcharge} = surcharge_{value} \cdot ( (base_{width}-stem_{offset}-stem_{width} ) \)
\( W_{surcharge} = 17.237 kN/m \cdot (2.210-0.686-0.305)m\)
\( W_{surcharge} = 21.012 kN/m\)
Restaurando o momento:
O momento restaurador é o responsável por evitar que a parede gire em relação ao canto mais inferior esquerdo da base. Para calculá-lo, é necessário realizar um somatório de momentos em relação ao ponto mencionado de todas as cargas verticais:
\(M_{stem}=W_{stem}\cdot d_{stem} = 22.467\;kN/m \cdot 0.839\;m=18.839\;kNm/m\)
\(M_{base}=W_{base}\cdot d_{base} = 18.855\;kN/m \cdot 1.105\;m=21.939\;kNm/m\)
\(M_{active}=W_{active}\cdot d_{active} = 71.784\;kN/m \cdot 1.601\;m=114.89\;kNm/m\)
\(M_{surcharge}=W_{surcharge}\cdot d_{surcharge} = 21.012\;kN/m \cdot 1.601\;m=33.630\;kNm/m\)
\( \Sigma{M_{R}} = M_{stem}+M_{base}+M_{active}+M_{surcharge}\)
\( \Sigma{M_{R}} = 18.839+21.939+114.89+33.630\)
\( \Sigma{M_{R}} = 189.298\;kNm/m\)
Cargas horizontais:
Todas as cargas horizontais às quais o muro de arrimo cantilever de concreto está submetido são mostrados na figura a seguir:
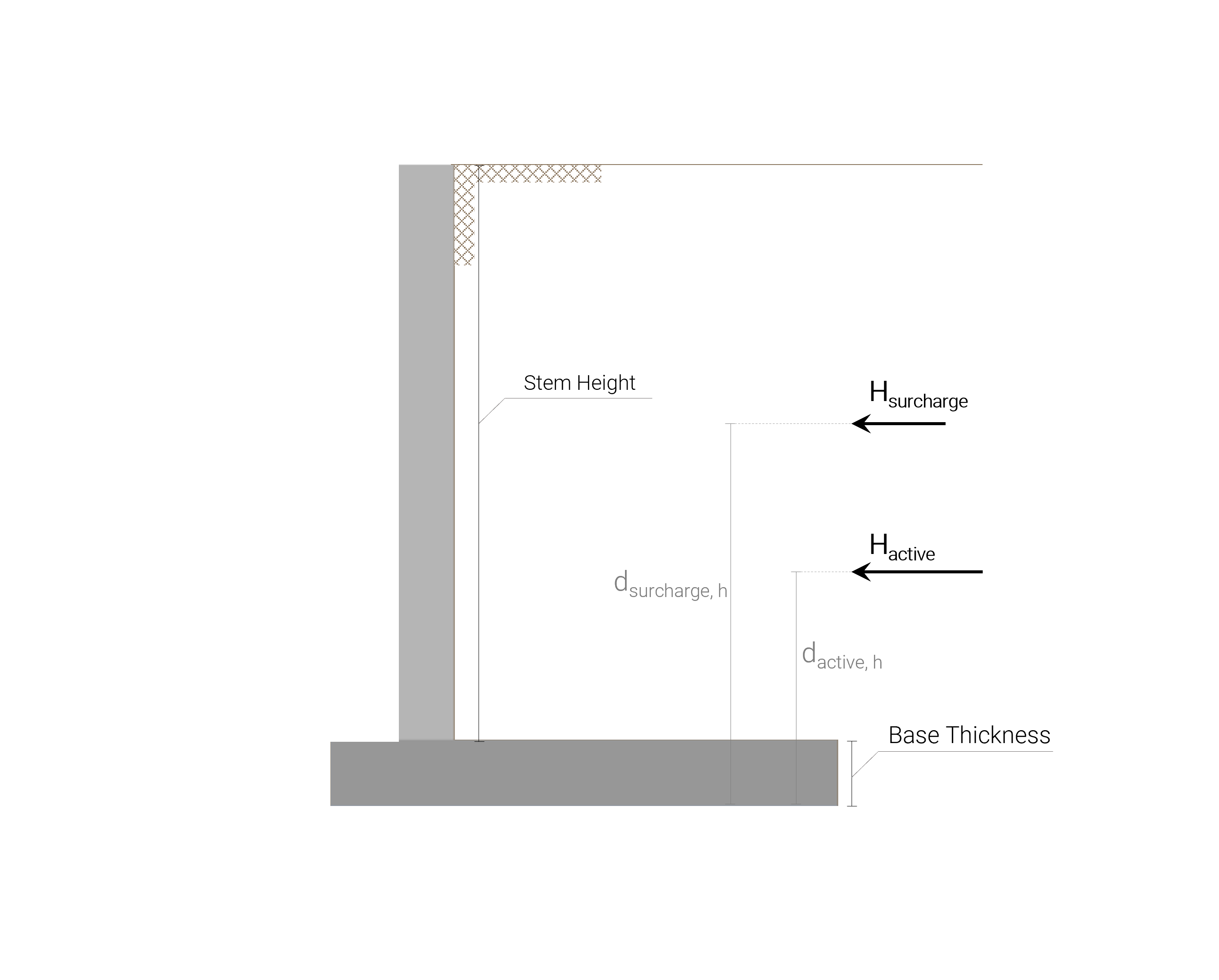
a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga, a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga:
\( K_a = \frac{1-sin(\gamma_{soil,\;active})}{1+sin(\gamma_{soil,\;active})} \)
\( K_a = \frac{1-sin(35º)}{1+sin(35º)} = 0.271 \)
a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga, a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga:
\(H_{active} = \frac{1}{2} \cdot \gamma_{soil,\;active} \cdot (stem_{height} + base_{thickness})^{2} \cdot K_a \)
\(H_{active} = \frac{1}{2} \cdot 18.85\;kN/m^3 \cdot 3.505^{2} \cdot 0.271 \)
\(H_{active} = 31.377\;kN/m \)
a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga, a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga, a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga:
\( h_{soil,\;eq} = \frac{surcharge_{value}}{\gamma_{soil,\;active}} = \frac{17.237 \;kN/m^{2}}{18.85 \;kN/m^{3}} \)
\( h_{soil,\;eq} = 0.914 \; m \)
\( H_{surcharge} = \gamma_{soil,\;active} \cdot h_{soil,\;eq} \cdot (stem_{height} + base_{thickness}) \cdot K_a\)
\(H_{surcharge} =\cdot 18.85\;kN/m^3 \cdot 0.914 \; m \cdot 3.505 \; m \cdot 0.271 \)
\(H_{surcharge} = 16.372\;kN/m \)
Momento de capotamento
O momento de tombamento é calculado como o momento gerado pelas cargas horizontais em relação ao canto inferior esquerdo da base. A distância do braço da alavanca para cada uma das cargas horizontais será:
- Um terço da altura da parede do fundo da base para o resultante da distribuição de pressão ativa do solo retido. É assim porque essa pressão segue uma distribuição triangular com um valor zero no nível da superfície e um valor máximo na parte inferior do nível de base.
- Metade da altura da parede a partir do fundo da base para o caso do carga horizontal resultante da presença da carga de sobretaxa. É assim desde que essa pressão segue uma distribuição retangular.
Dito isto, o momento de tombamento é calculado da seguinte forma:
\( M_{active} = H_{active} \cdot \frac{1}{3} \; (stem_{height} + base_{thickness}) \)
\( M_{active} = 31.377\;kN/m \cdot \frac{1}{3} \; 3.505\;m \)
\( M_{active} = 36.659 \;kNm/m \)
\( M_{surcharge, \;h} = H_{surcharge} \cdot \frac{1}{2} \; (stem_{height} + base_{thickness}) \)
\( M_{surcharge, \;h} = 16.372\;kN/m \cdot \frac{1}{2} \; 3.505\;m \)
\( M_{surcharge, \;h} = 28.692\;kNm/m \)
\( \Sigma{M_{OTM}} = M_{active}+M_{surcharge, \;h}\)
\( \Sigma{M_{OTM}} = 36.659 \;kNm/m+28.692\;kNm/m\)
\( \Sigma{M_{OTM}} = 65.351\;kNm/m\)
Fator de segurança contra capotamento
ACI 318 cdot K_a \(2.0\). É calculado da seguinte forma:
\( FS = \frac{\Sigma{M_{R}}}{\Sigma{M_{OTM}}} \)
\( FS = \frac{189.298\;kNast m}{65.351\;kNast m}= 2.897 \ge 2.0\) cdot K_a!
Calculadora de muros de arrimo
Neste artigo, discutimos exemplos de cálculo de momento de tombamento. A SkyCiv oferece uma calculadora gratuita de muros de arrimo que verifica o momento de tombamento e realiza uma análise de estabilidade em seus muros de arrimo. A SkyCiv oferece uma calculadora gratuita de muro de arrimo que verifica o deslizamento no muro de arrimo e realiza uma análise de estabilidade em seus muros de arrimo, para que você possa ver o passo a passo de como calcular a estabilidade do muro de contenção contra tombamento, A SkyCiv oferece uma calculadora gratuita de muro de arrimo que verifica o deslizamento no muro de arrimo e realiza uma análise de estabilidade em seus muros de arrimo!
Desenvolvedor de Produto
BEng (Civil)
