Índice
- Cálculo do diagrama do momento de flexão
- e pode ser adaptado a muitos tipos diferentes de problemas
- Convenção de sinais para diagramas de momento fletor
- Como calcular a flexão usando o feixe SkyCiv
Cálculo do diagrama do momento de flexão
Abaixo estão instruções simples sobre como calcular o diagrama de momento fletor de um viga simplesmente apoiada. Estude este método, pois é muito versátil (e pode ser adaptado a muitos tipos diferentes de problemas. A capacidade de calcular o momento de um feixe é uma prática muito comum para engenheiros estruturais e muitas vezes aparece em exames de faculdade e ensino médio. é bom avisar antes, que o software SkyCiv Beam pode exibir esses os cálculos manuais instantaneamente e automaticamente! Seguiremos o tutorial de hoje com um exemplo retirado diretamente do Módulo de Cálculo Manual do SkyCiv Beam.
em primeiro lugar, o que é uma momento fletort? Um momento é uma força rotacional que ocorre quando uma força é aplicada perpendicularmente a um ponto a uma determinada distância daquele ponto. É calculado como a força perpendicular multiplicada pela distância do ponto. Um momento de flexão é simplesmente a dobra que ocorre em uma viga devido a um momento.
É importante lembrar duas coisas ao calcular os momentos de flexão; (1) as unidades padrão são Nm e (2) quando a fibra superior é comprimida, a flexão é considerada positiva. Com as definições fora do caminho, vamos dar uma olhada nas etapas para calcular um diagrama de momento fletor:
e pode ser adaptado a muitos tipos diferentes de problemas
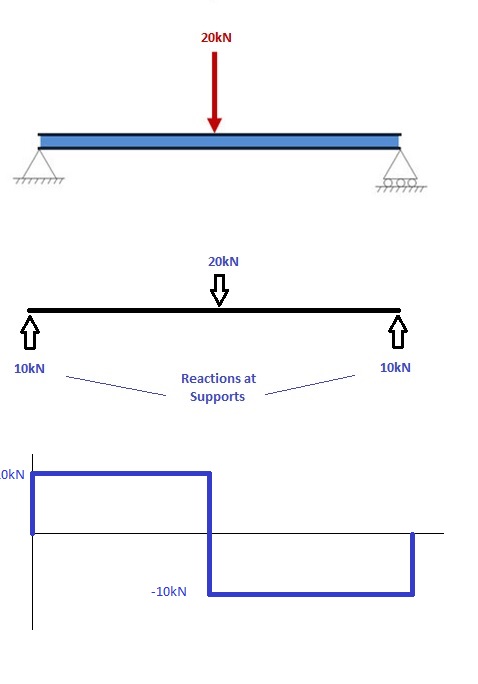
1. Calcule as reações nos apoios e desenhe o Diagrama de Corpo Livre (FBD)
Se você não tem certeza de como determinar as reações nos apoios – por favor veja este tutorial primeiro. Depois de ter as reações, desenhe seu Diagrama de Corpo Livre e Diagrama de força de corte debaixo da viga. Finalmente, o cálculo dos momentos pode ser feito nas seguintes etapas:
2. Da esquerda para a direita, faço “cortes” antes e depois de cada reação / carga
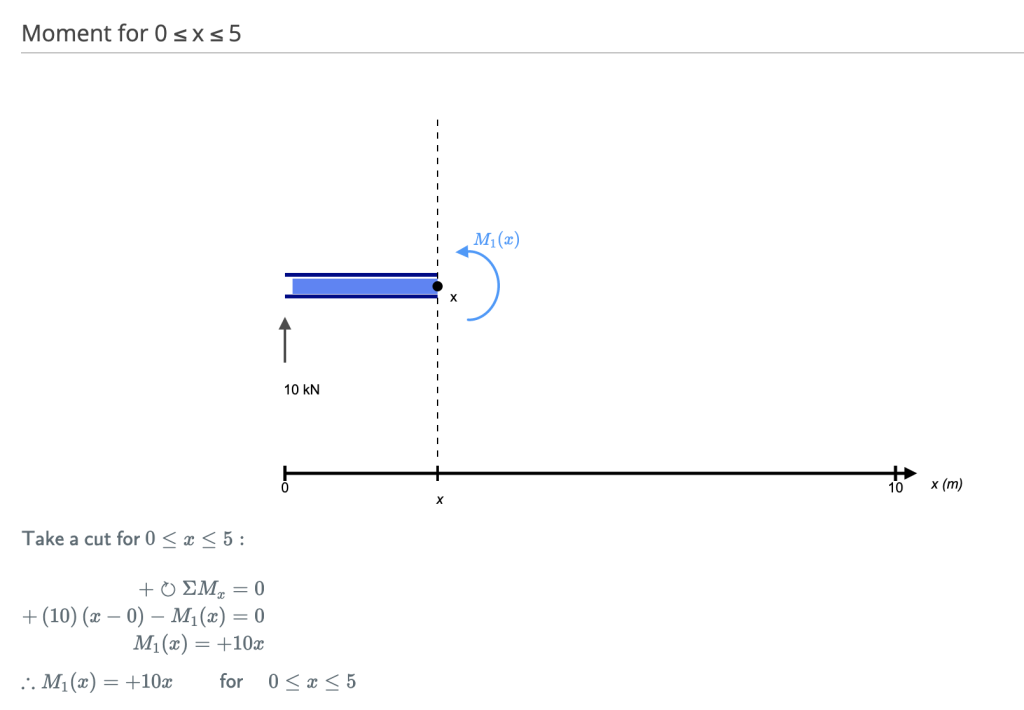
Para calcular o momento fletor de uma viga, devemos trabalhar da mesma forma que fizemos para o diagrama de força de cisalhamento. Começando em x = 0 vamos mover através da viga e calcular o momento de flexão em cada ponto.
Cortar 1
Faça um “cortar” logo após a primeira reação do feixe. Em nosso exemplo simples:
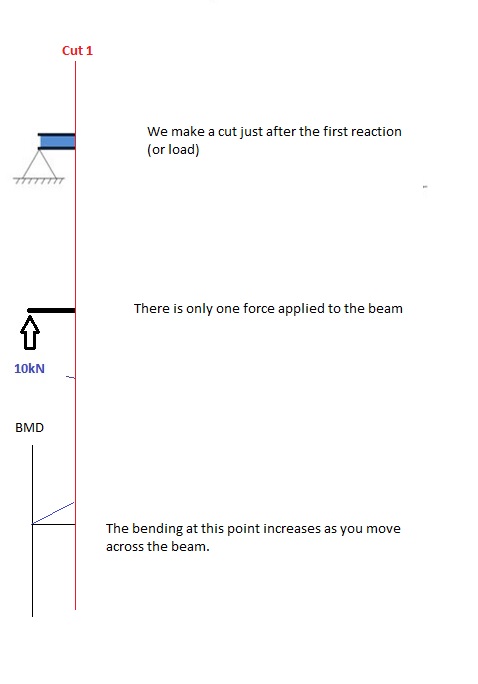
[Fonte: SkyCiv Módulo de cálculo manual da viga]
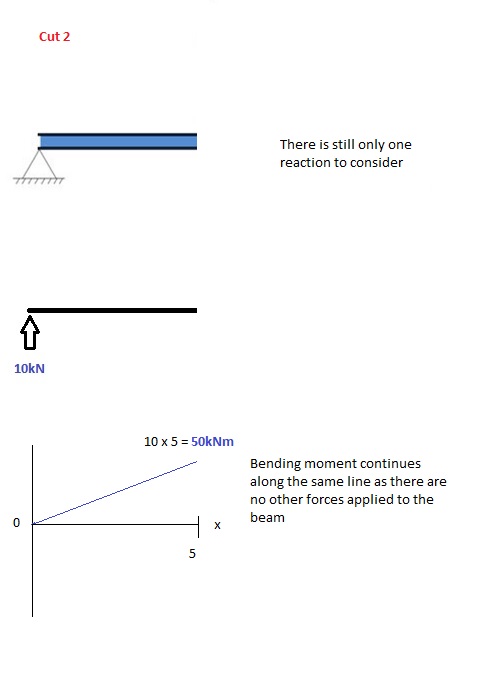
Cortar 2
Este corte é feito um pouco antes da segunda força ao longo da viga. Uma vez que não há outras cargas aplicadas entre o primeiro e o segundo corte, a equação do momento fletor vai continuar o mesmo. Isso significa que podemos calcular o momento fletor máximo (neste caso, no ponto médio, ou x = 5) simplesmente substituindo x = 5 na equação acima:
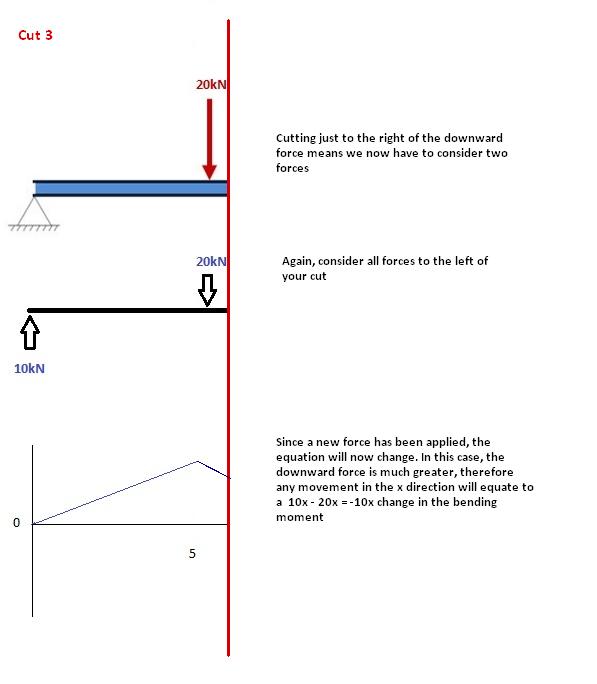
Cortar 3
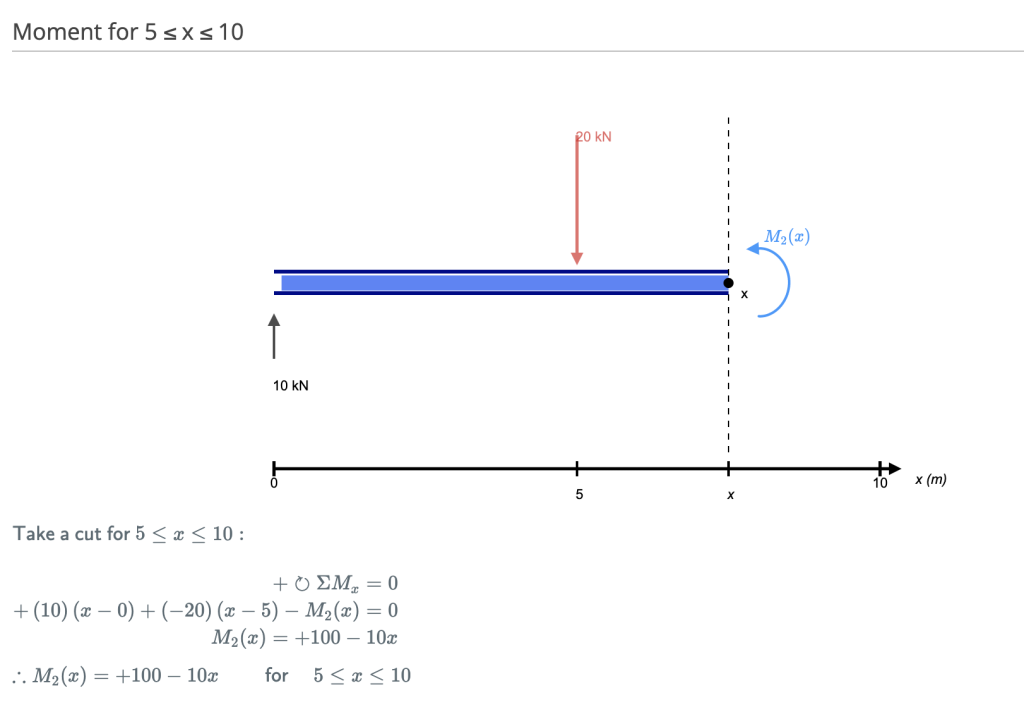
Este corte é feito logo após a segunda força ao longo da viga. Agora temos DUAS forças que atuam à esquerda do nosso corte: uma reação de suporte de 10kN e uma carga de ação descendente de -20kN. Portanto, agora devemos considerar essas duas forças à medida que progredimos ao longo de nosso feixe. Para cada metro que nos movemos através do feixe, haverá um momento de + 10kNm adicionado da primeira força e -20kNm da segunda.
Cortar 4
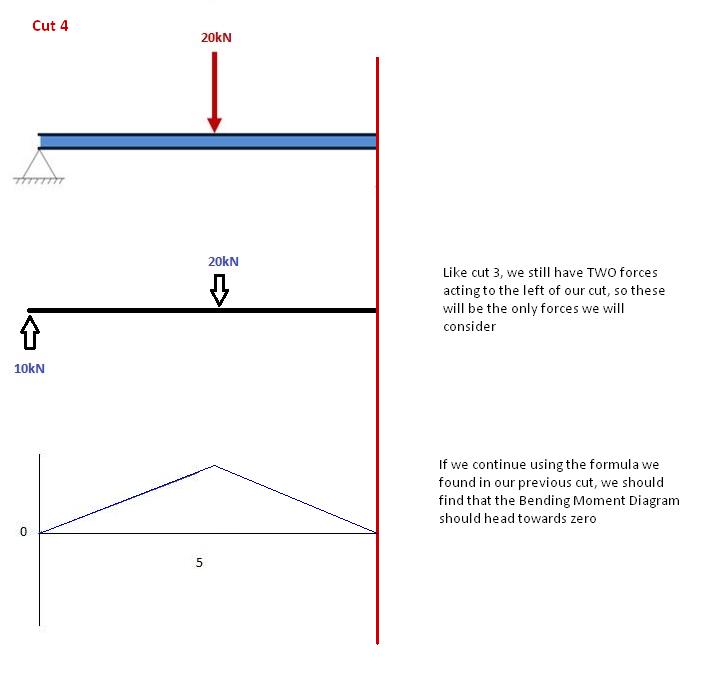
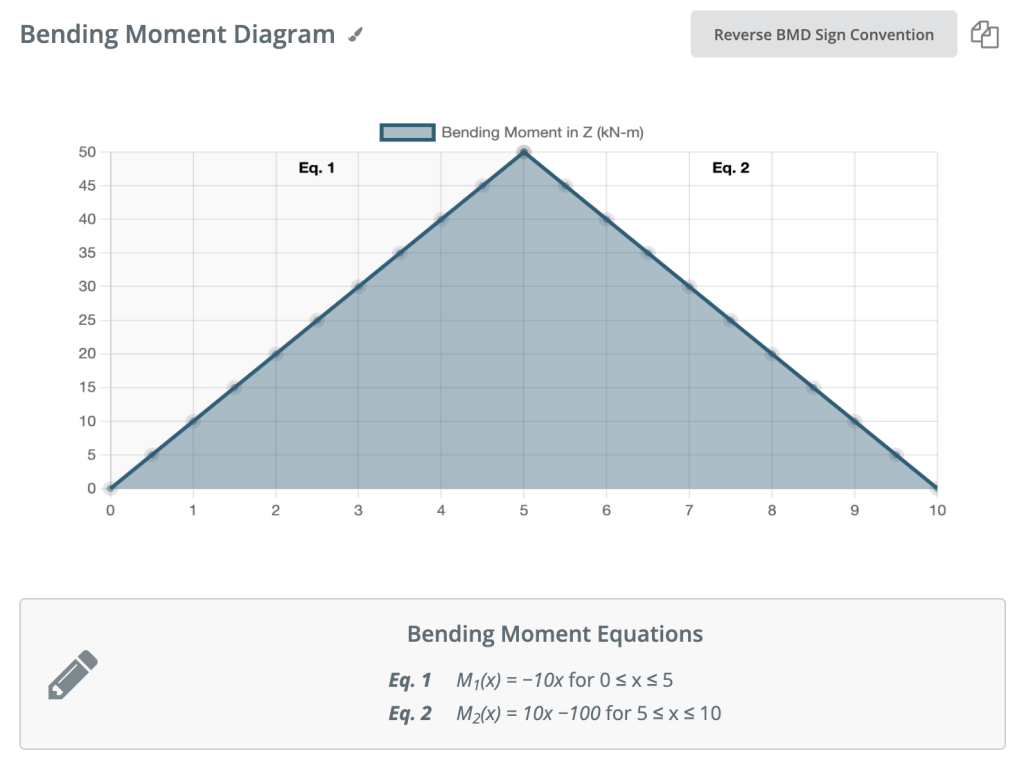
Novamente, vamos nos mover para a direita de nossa viga e fazer um corte um pouco antes de nossa próxima força. Nesse caso, nosso próximo corte ocorrerá um pouco antes da reação do Suporte Certo. Uma vez que não há outras forças entre o suporte e nosso corte anterior, a equação permanecerá a mesma: M(x) = 50 -10(x-5) pra 5 ≤ x≤ 10 E vamos substituir x = 10 nisso para encontrar o momento de flexão encontrado no final da viga: M(x) = 50 – 10(10-5) = 0kNm Isso faz todo o sentido. Uma vez que nosso feixe é estático (e sem rotação) faz sentido que nosso feixe deva ter momento zero neste ponto quando consideramos todas as nossas forças. Também satisfaz uma das nossas condições iniciais, que a soma dos momentos no suporte é igual a zero. NOTA: Se seus cálculos o levarem a qualquer outro número que não seja 0, você cometeu um erro!
Convenção de sinais para diagramas de momento fletor
Discutimos como encontrar o momento fletor acima. Os diagramas de momento fletor podem ficar um pouco confusos quando se trata de convenções de sinais. Você pode ver o mesmo diagrama desenhado em direções opostas, dependendo da fonte. A convenção de sinais usada pelo SkyCiv é exibida abaixo.
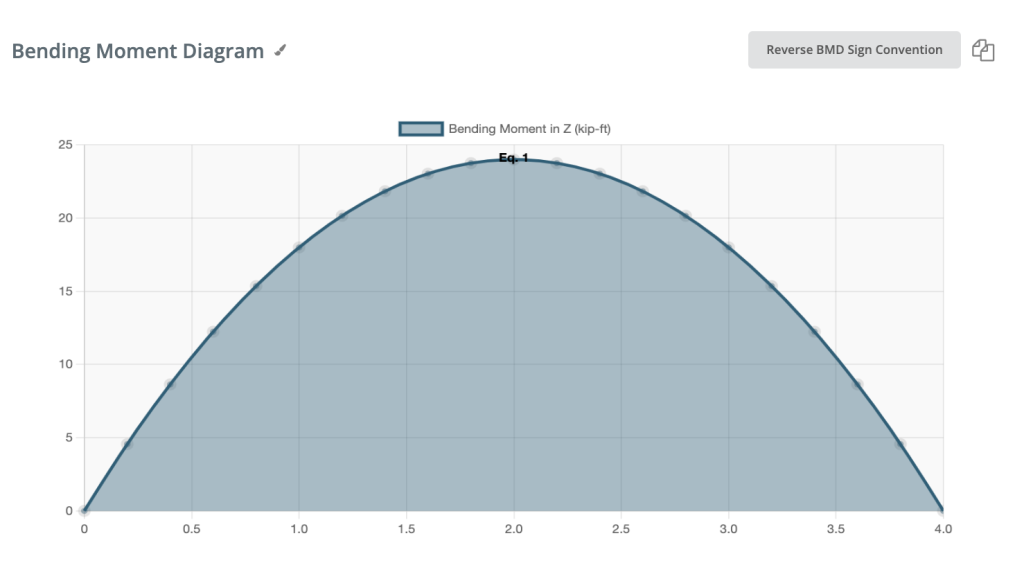
Momento de flexão positivo:
Se o momento fletor for positivo, a fibra superior da viga é comprimida.
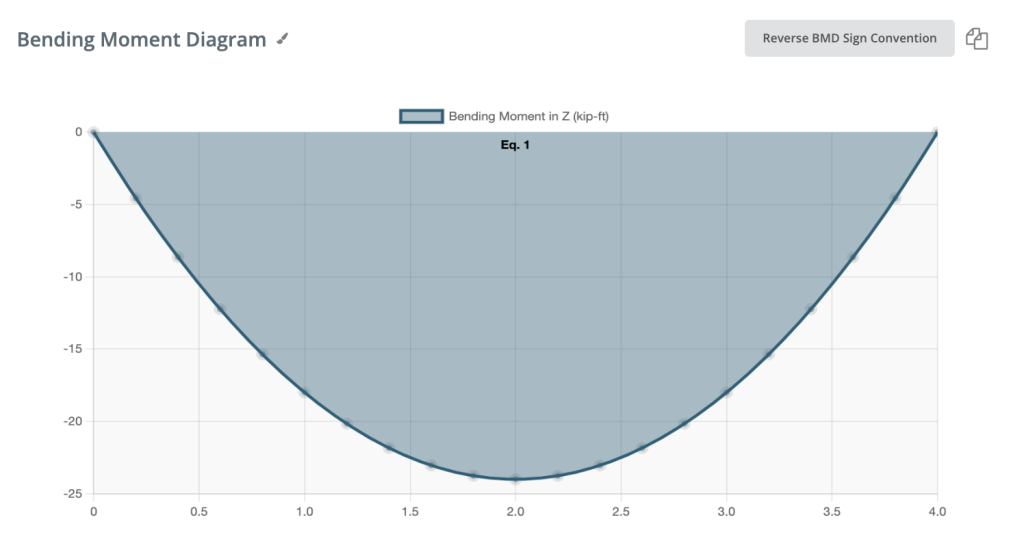
Momento de flexão negativo:
Se o momento fletor for negativo, a fibra inferior da viga é comprimida.
BÔNUS: Como encontrar o momento fletor
Em nossa versão paga do SkyCiv Beam a calculadora mostrará os cálculos manuais completos e as etapas executadas para calcular manualmente seus diagramas de momento fletor. Simplesmente modele seu feixe usando a calculadora, e clique em resolver. Ele mostrará os cálculos passo a passo de como desenhar um diagrama de momento fletor (incluindo cortes):
SkyCiv também tem um a Calculadora de vigas grátis para você calcular diagramas de momento fletor rápida e facilmente. Também calcula reações em apoios, dos diagramas de força de corte, e as deflexões e relações de extensão. Então confira agora ou inscreva-se hoje para começar SkyCiv Beam!
De outra forma, se você deseja calcular a capacidade do momento fletor para uma viga em I, experimente o nosso Calculadora de Carga I-Beam!

