Guia de cálculo para projetar uma sapata isolada com base na CSA A23.3-14
A SkyCiv Foundation cobre o projeto de sapata isolada em conformidade com CSA A23.3-14¹ e NBCC 20102.
Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta permite que os usuários realizem cálculos de Foundation Design sem nenhum download ou instalação!
Parâmetros de projeto de uma sapata isolada
Alguns cálculos apresentados são semelhantes ao ACI 318, que também é uma das referências do seu homólogo CSA.
Requisitos de Dimensão
Para determinar as dimensões de uma sapata isolada, serviço ou cargas não fatoradas, como morto (D), Viver (eu), Vento (C), Sísmica (E), etc serão aplicados usando combinações de carga, conforme definido pela NBCC 2010. Qualquer combinação de carga governar será considerada a carga do projeto, e será dividido pela pressão permitida do solo, conforme mostrado na Equação 1.
\(\texto{A} = frac{\texto{P}_{\texto{n}}}{\texto{q}_{\texto{tudo}}} \seta direita \) Equação 1
Onde:
qtudo = pressão permitida do solo
Pn = carga de projeto não fatorada
A = área da fundação
Tesoura unidirecional
Para verificar cisalhamento unidirecional, o plano de cisalhamento crítico (Consulte a Figura 1) está localizado a uma distância “d” da face de uma coluna.
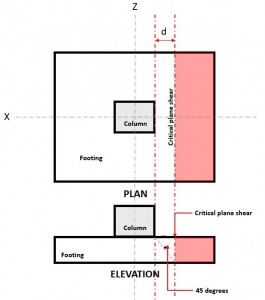
Figura 1. Cisalhamento plano crítico de cisalhamento unidirecional
A Mão única Cisalhamento Demanda ou Vf é calculado assumindo que a sapata está em balanço longe da coluna onde a área é (vermelho) indicado na figura 2, de acordo com CSA A23.3-14, Seção 13.3.6.
A Capacidade de cisalhamento unilateral ou Vc é definida como resistência ao cisalhamento final e calculada usando a Equação 2 por CSA A23.3-14, Seção 11.3.4.
\(\texto{V}_{\texto{c}} = phi _{\texto{c}} \times lambda times sqrt{\texto{f ’}_{\texto{c}}} \times text{b}_{\texto{C}} \times text{d} \seta direita \) Equação 2 (CSA A23.3-14 Eq.. 11-6)
Onde:
ϕc = fator de resistência para concreto
λ = fator de modificação para densidade do concreto
f’c = resistência do concreto especificada, MPa
bC = largura da base, milímetros
d = profundidade de cisalhamento efetiva, milímetros
A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender aos requisitos de projeto de CSA A23.3-14:
\(\texto{V}_{\texto{f}} \leq phi text{V}_{\texto{c}} \seta direita \) Equação 3 (CSA A23.3-14 Eq. 11.3)
Fundação SkyCiv, em conformidade com a Equação 3, calcula a razão de unidade de cisalhamento unilateral (Equação 4) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Razão de Unidade} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 4
Cisalhamento de duas vias
A Cisalhamento de duas vias estado limite, também conhecido como punção, estende a seção crítica a uma distância “d/2” da face da coluna e ao redor do perímetro da coluna. O Plano de Cisalhamento Crítico está localizado nessa seção da sapata (Consulte a Figura 2).
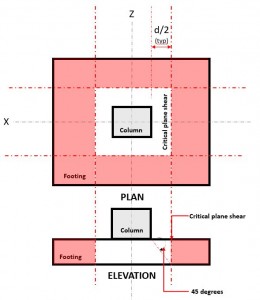
Figura 2. Plano de cisalhamento crítico de cisalhamento bidirecional
A Dois caminhosouvir Demanda ou Vf ocorre no plano de cisalhamento crítico, localizado a uma distância de “d/2” onde o (vermelho) área hachurada, indicado na figura 2, de acordo com CSA A23.3-14, Seção 13.3.3.
A Capacidade de cisalhamento ou Vc é regido pelo menor valor calculado usando a Equação 5, 6, e 7 por CSA A23.3-14, Seção 13.3.4.1
\(\texto{V}_{\texto{c}} = left ( 1 + \fratura{2}{\inclui cálculos detalhados passo a passo{\texto{c}}} \direito ) \vezes 0.19 \vezes lambda vezes phi _{\texto{c}} \times sqrt{f’_{c}} \seta direita \) Equação 5 (CSA A23.3-14 Eq. 13.5)
\(\texto{V}_{\texto{c}} = left ( \fratura{\alfa_{\texto{s}} \times text{d}}{\texto{b}_{\texto{o}}} + 0.19 \direito ) \vezes lambda vezes phi _{\texto{c}} \times sqrt{f’_{c}} \seta direita \) Equação 6 (CSA A23.3-14 Eq. 13.6)
\(\texto{V}_{\texto{c}} = 0.38 \vezes lambda vezes phi _{\texto{c}} \times sqrt{f’_{c}} \seta direita \) Equação 7 (CSA A23.3-14 Eq. 13.7)
Observação: bc é a razão entre o lado longo e o lado curto da coluna, carga concentrada, ou área de reação e αs É dado por 13.3.4.1
Onde:
λ = fator de modificação para densidade do concreto
f’c = resistência especificada do concreto à compressão, MPa
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, milímetros
A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender aos requisitos de projeto da CSA A23.3-14:
\(\texto{V}_{\texto{f}} \leq phi text{V}_{\texto{c}} \seta direita \) Equação 8 (CSA A23.3-14 Eq. 11.3)
Fundação SkyCiv, em conformidade com a Equação 8, calcula a razão da unidade de cisalhamento bidirecional (Equação 9) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Razão de Unidade} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 9
Flexure
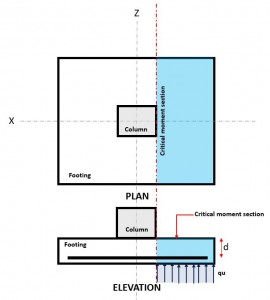
Figura 3. Seção Crítica de Flexão
A Flexural estado limite ocorre em a seção de flexão crítica, localizado na face da coluna no topo da sapata (Consulte a Figura 3).
A Demanda Momentânea, ou Mf está localizado na Seção de Flexão Crítica (área de hachura azul) indicado na figura 3, e é calculado usando a Equação 10.
\( \texto{M}_{você} = text{q}_{você} \times left ( \fratura{eu_{x}}{2} – \fratura{c_{x}}{2} \direito ) \vezes l_{z} \times left ( \fratura{\fratura{eu_{x}}{2} – \fratura{c_{x}}{2} }{2} \direito ) \seta direita \) Equação 10
Onde:
qvocê = pressão do solo fatorada, kPa
eux = dimensão da base ao longo do eixo x, milímetros
euz = dimensão da base ao longo do eixo z, milímetros
cx = dimensão da coluna ao longo do eixo x, milímetros
A Resistência ao momento, ou Mr é calculado usando a Equação 11.
\( \texto{M}_{r} = phi_{\texto{s}} \vezes A_{s} \vezes f_{sim} \times left( d – \fratura{uma}{2} \direito) \seta direita \) Equação 11
Onde:
ϕs = fator de resistência para barras de armadura não protendidas
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, milímetros
As = área de reforço, milímetros2
a = profundidade do bloco de tensão retangular equivalente, milímetros
fy = resistência do reforço, MPa
A demanda de momento e a resistência ao momento devem atender à seguinte equação para atender aos requisitos de projeto da CSA A23.3-14:
\(\texto{M}_{\texto{r}} \leq phi text{M}_{\texto{f}} \seta direita \) Equação 12
Fundação SkyCiv, em conformidade com a Equação 12, calcula a razão da unidade de flexão (Equação 13) tomando Flexural Demand em vez de Flexural Capacity.
\( \texto{Razão de Unidade} = frac{\texto{Flexure Demand}}{\texto{Capacidade de Flexão}} \seta direita \) Equação 13
NOVA Fundação SkyCiv com FEA
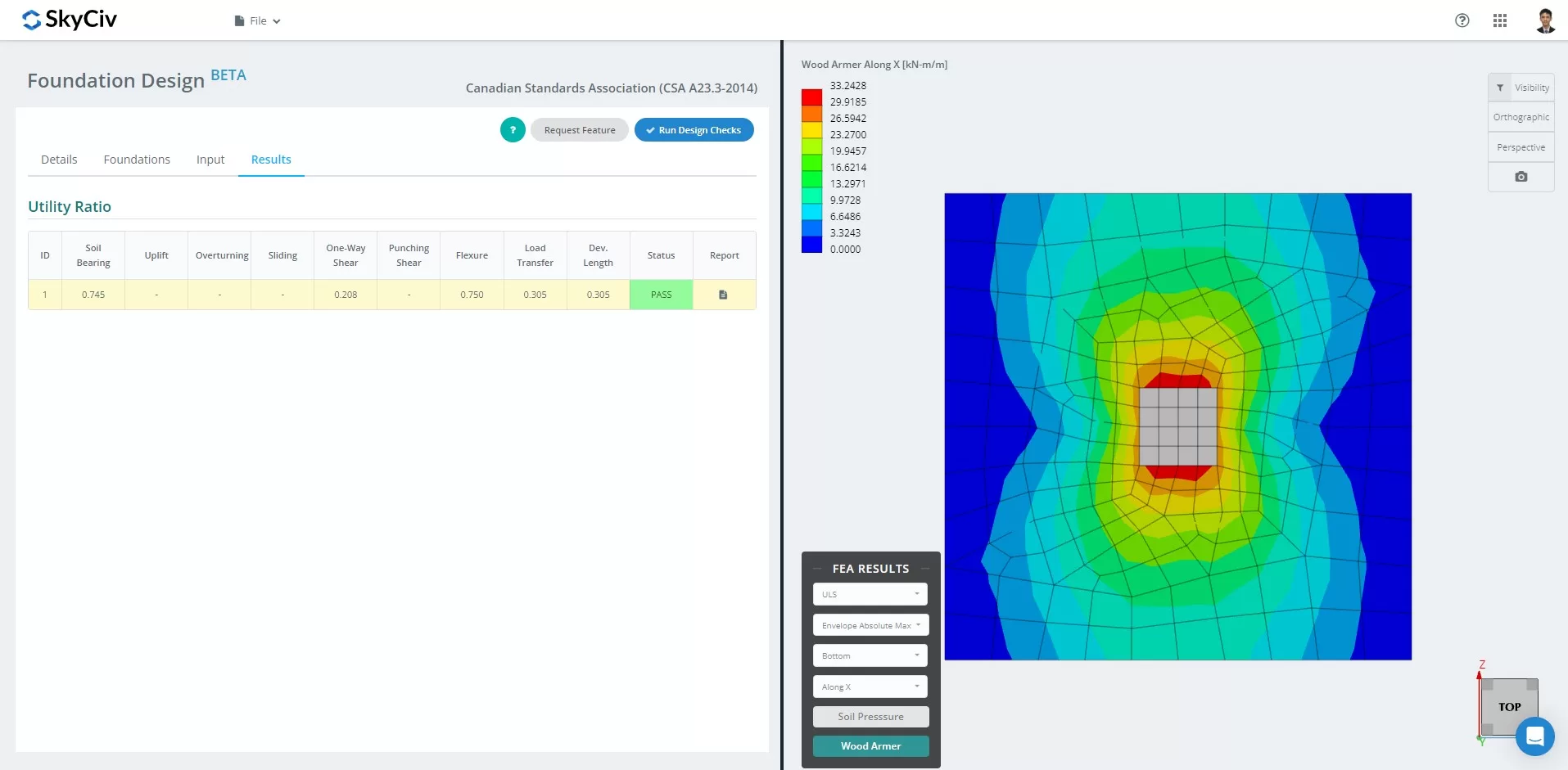
A partir de março 2024, o Módulo Foundation Design integrou a Análise de Elementos Finitos (FEIO) solucionador em suas capacidades. Este novo recurso permite que os usuários realizem análises aprofundadas da pressão do solo e da armação de madeira, ao mesmo tempo em que realizam todas as verificações estruturais especificadas pela CSA A23.3-14., incluindo todas as verificações mencionadas acima. O resumo dos resultados da FEA está incluído no relatório abrangente.
Calculadora grátis para pés de concreto
Experimente a calculadora gratuita de sapatas de concreto SkyCiv para projetar fundações para sapatas, sapatas combinadas, estacas de concreto, almofadas de concreto, e mais.
Referências
- A23.3-14: Projeto de estruturas de concreto. Associação Canadense de Normas, 2014.
- Brzev e Pao. Projeto de concreto armado: Uma Abordagem Prática, 2009.
Desenvolvedor de Produto
bacharelado (Civil)


