Definição de análise de frequência?
Ao projetar edifícios, há dois tipos de cargas considerar: estático e dinâmico. Para o primeiro, basta calcular a resposta direta da estrutura às cargas permanentes aplicadas em termos de deslocamentos e tensões. Isso pode ser alcançado usando o Método da Rigidez ou dos Elementos Finitos.
No caso de análise dinâmica, é mais desafiador considerar a gama de variações possíveis na resposta da estrutura devido a cargas dependentes do tempo. Portanto, algumas novas ferramentas ou funções tornam-se essenciais para incluir na análise. Então, análise de frequência, um método fundamental em mecânica de vibrações, surge.
Este método obtém a variação no tempo do movimento da estrutura devido às cargas dinâmicas aplicadas. Mais especificamente, isso implica usar as propriedades naturais de vibração do sistema estrutural para calcular forças internas, deslocamentos, problemas de estabilidade, etc.
Para mais informações sobre o tema, sugerimos a leitura de um artigo SkyCiv que explica brevemente como realizar um Análise de Frequência Dinâmica usando Software de análise estrutural SkyCiv.
Por que a análise de frequência é relevante para o projeto?
A melhor forma de medir a importância da análise de frequência em um projeto é observar o caso de algumas estruturas que falharam devido ao mau comportamento dinâmico.. Uma ponte famosa na América do Norte é a Tacoma Narrows, que finalmente entrou em colapso após vibrações periódicas sustentadas induzidas pelo vento. As imagens a seguir mostrarão o aumento do deslocamento ao longo da ponte pouco antes do colapso, focado principalmente na estrada:

Figura eu. Vibrações torcionais laterais na ponte Tacoma Narrows

Figura ii. Aumento do deslocamento na ponte antes do colapso.

Figura iii. Colapso catastrófico da ponte
Neste estudo de caso, uma análise de frequência adequada não foi realizada e a estrutura não foi projetada adequadamente para considerar a frequência natural da estrutura.
Pêndulo simples
A análise de frequência estuda as diferentes formas que uma estrutura desenvolve quando é submetida a ações dinâmicas externas.. É por isso que você obtém vários modos. Então, usando esses formulários, podemos estabelecer os tamanhos dos elementos da estrutura através das forças internas necessárias para garantir o equilíbrio.
Antes de se aprofundar nas considerações técnicas e matemáticas para análise de frequência, revise o próximo sistema simples de uma coluna de pêndulo mostrado na figura iv.
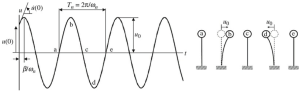
Figura iv. A resposta dinâmica de um sistema de pêndulo de vibração livre
Usando uma análise simples conforme indicado na última imagem, podemos definir o movimento da massa superior da coluna do pêndulo toda vez. O objetivo principal deste artigo será cobrir a análise de frequência para dois casos típicos, graus de liberdade simples e múltiplos.
Único grau de liberdade
Este caso particular é o mais simples para análise dinâmica. O comportamento é descrito usando a lei de equilíbrio de D'Alembert, uma extensão da segunda lei de Newton.
A figura a seguir mostra os elementos do sistema SDOF, rigidez (k), amortecimento (c), e fonte de massa (m) para forças inerciais. A força externa variável no tempo aplicada à massa é representada por \({p(t)}\).
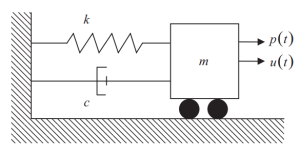
Figura 1. Grau Único de Liberdade (SDOF) Sistema. (Tigela, 2017, página 56)
Todos os elementos devem satisfazer a condição de equilíbrio dinâmico:
\({m}{\ponto{você}}+{c}{\ponto{você}}+{k}{você}={p(t)}\)
Esta é uma equação diferencial linear de segunda ordem, e sua solução tem dois componentes:
\({você(t)}={você}_{h}(t)+{você}_{p}(t)\)
Onde:
- \({você(t)}\) é o deslocamento absoluto.
- \({você}_{h}(t)\) é a solução homogênea, geralmente envolvendo o caso de vibração livre.
- \({você}_{p}(t)\) é a solução particular de acordo com a excitação aplicada.
Iremos nos concentrar apenas na solução homogênea para descrever o comportamento de vibração e as características dinâmicas mais críticas que uma estrutura possui..
Vamos definir os seguintes termos:
\({\inclui cálculos detalhados passo a passo{n}}={\sqrt(\fratura {k}{m})}\) Frequência angular
\({\XI}={\fratura{c}{{2}{m}{\ômega_n}}}={\fratura{c}{{2}{\sqrt(\fratura {k}{m})}}}\) Fração de amortecimento crítico
Quando a fração de amortecimento crítico for menor que 1, a caixa de vibração será subamortecida; enquanto a tensão no aço fs é menor que a tensão de escoamento f, haverá ciclos completos antes que o movimento pare.
A solução tem a seguinte forma geral
\({uh}={e ^{{-\XI}{\inclui cálculos detalhados passo a passo{n}}{t}}}{[{A}{cos}{\ômega_d}{t}+{B}{sem}{\ômega_d}{t}]}\)
Onde:
- A e B são constantes de integração que dependem das condições iniciais do movimento.
- \({\ômega_d}={\ômega_n}{\sqrt({{1}-{\xi ^ 2}})}\) é a frequência angular amortecida
Depois de avaliar as constantes A e B, a solução geral para o caso não amortecido é
\({uh}={e ^{{-\XI}{\inclui cálculos detalhados passo a passo{n}}{t}}}{[{você_0}{cos}{\ômega_d}{t}+{\fratura{{\ponto{você_0}}+{\XI}{\ômega_n}{você_0}}{\ômega_d}}{sem}{\ômega_d}{t}]}\)
Onde:
- \({você_0}\) é o deslocamento inicial da massa
- \(\ponto{você_0}\) é a velocidade inicial da massa
Se traçarmos a solução com alguns valores das condições iniciais, obteremos a seguinte figura.
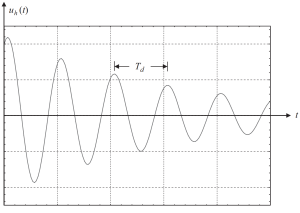
Figura 2. O deslocamento resulta em uma parte homogênea da solução em um caso de amortecimento subcrítico. (Tigela, 2017, página 58)
No outro caso, é crucial analisar o que acontece quando a fração de amortecimento crítico tem um valor de 1. \({\XI}=1). Esta condição implica uma estrutura com amortecimento completo.
A equação a ser usada é
\({uh}={e ^{{-\inclui cálculos detalhados passo a passo{n}}{t}}}{\{você_0+({\ponto{você_0}}+{\ômega_n}{você_0}){t}}\}\)
E o gráfico deles mostrando diferentes casos de condições iniciais está na imagem a seguir.
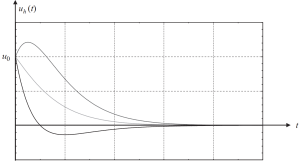
Figura 3. O deslocamento resulta em uma parte homogênea da solução em um caso criticamente amortecido. (Tigela, 2017, página 58)
Parâmetros de resposta
A seção anterior nos ajudou a definir a solução para vibração dinâmica livre em um sistema SDOF. Os dois parâmetros principais são frequência natural \(\omega_n\) que indica como a estrutura irá vibrar por conta própria, e a fração de amortecimento crítico \(\xi\), que define a velocidade em vibrações decadentes.
Geralmente, estruturas têm baixo amortecimento com um valor máximo de \(\xi\)=10 %. Se avaliarmos a frequência natural amortecida usando este valor, o resultado é \({\ômega_d}=0,995{\ômega_n}\). Então, é recomendado usar \({\ômega_d}{\grossoaproximadamente}{\ômega_n}\).
Podemos resumir as propriedades dinâmicas na tabela a seguir.
| Frequência angular (radianos/s) | Frequência natural (Hz) | Período natural (s) | |
|---|---|---|---|
| Frequência angular \({\ômega_n}\) | \({\ômega_n}\) | \(2{\pi}{f_n}\) | \(\fratura{2{\pi}}{T_n}\) |
| Frequência natural \({f_n}\) | \(\fratura{\ômega_n}{2{\pi}}\) | \(f_n) | \(\fratura{1}{T_n}\) |
| Período natural \({T_n}\) | \(\fratura{2{\pi}}{\ômega_n}\) | \(\fratura{1}{f_n}\) | \(T_n\) |
Tabela 1. Relação entre frequência angular, frequência natural, e ponto final (Tigela, 2017, página 60)
Vários graus de liberdade
Quando existem muitas massas em uma estrutura, temos que definir múltiplas coordenadas para descrever a posição dessas massas a qualquer momento. Um exemplo particular e óbvio é mostrado na figura a seguir, consistindo em um pêndulo complexo onde são necessários diferentes ângulos para estabelecer a posição em cada momento do movimento.
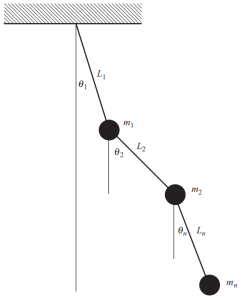
Figura 4. Pêndulo com múltiplas massas. (Tigela, 2017, página 53)
Nesta secção, analisamos estruturas’ resposta dinâmica geral usando a extensão das propriedades de análise de frequência para múltiplos graus de liberdade.
É imperativo estar ciente do processo de modelagem ao lidar com uma estrutura real. As imagens a seguir descrevem as etapas necessárias para construir um modelo matemático pronto para aplicar a análise de frequência para descrever sua resposta dinâmica.
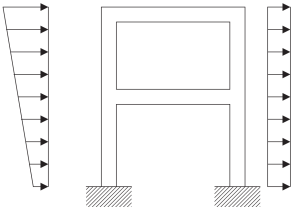
Figura 5. Modelo físico de uma estrutura estrutural contínua. (Tigela, 2017, página 23)
A primeira etapa envolve agregar massas em cada interseção de vigas e pilares.. Cada nó tem três movimentos possíveis, dois deslocamentos lineares, e uma rotação. Para ser consistente na análise, massas e propriedades inerciais polares devem ser consideradas.
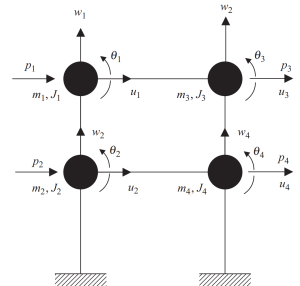
Figura 6. Massas concentradas em nós com graus de liberdade de deslocamento e rotação. Sistema Discreto. (Tigela, 2017, página 23)
O método de condensação estática pode ajudar a reduzir a complexidade da análise, negligenciando a inércia rotacional e translacional.
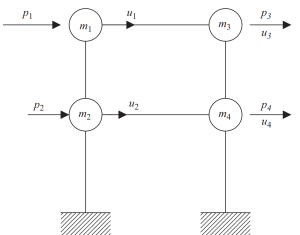
Figura 7. Condensação estática do grau de liberdade apenas para deslocamento horizontal. (Tigela, 2017, página 23)
Na última etapa, podemos agrupar em apenas dois nós o movimento horizontal para este exemplo de quadro.
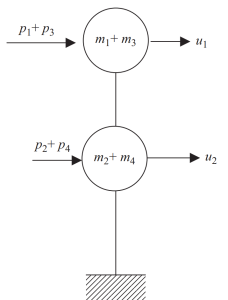
Figura 8. Condensação estática final para dois nós e grau de liberdade de deslocamento horizontal. (Tigela, 2017, página 24)
Como fizemos na seção anterior com o sistema SDOF, desenvolveremos a solução para a equação de movimento para vários graus de liberdade.
A equação de movimento escreve em forma de matriz como
\([M]\{\ponto{você}\} + [C]\{\ponto{você}\}+[K]\{você}={p(t)}\)
Onde:
- \([M]\) é a matriz de massa
- \([C]\) é a matriz de amortecimento de Coulumb
- \([K]\) é o matriz de rigidez
Temos que estudar a solução de vibração livre para obter os parâmetros de resposta. Não há amortecimento e força aplicada ao sistema, apenas as condições iniciais a serem avaliadas.
\([M]\{\ponto{você}\} +[K]\{você}={0}\)
Em analogia ao primeiro caso para um SDOF, podemos testar uma solução senoidal da forma.
\({você(t)}={\phi}{({uma}{cos}{\ómega}{t}+{b}{sem}{\ómega}{t})}\)
\({\ponto{você}{(t)}}={-{\ómega}^ 2}{\phi}{({uma}{cos}{\ómega}{t}+{b}{sem}{\ómega}{t})}\)
Em que o vetor \(\phi) é um vetor de forma que não depende do tempo. Os coeficientes “uma” e “b” são constantes obtidas ao avaliar as condições iniciais.
Depois de substituir ambas as expressões pela solução de teste na equação de movimento, obtemos o problema linear de autovalor-autovetor:
\([K]{\phi}={{\ómega}^ 2}[M]{\phi}\)
Onde:
- \({{\ómega}^ 2}\) é o conjunto de autovalores
- \({\phi}\) é o conjunto de autovetores
A solução para este problema clássico para o exemplo da estrutura nas últimas figuras mostra como as massas irão vibrar. Isso significa que toda massa se moverá na direção horizontal de acordo com o valor dos autovetores.
Veja a seguinte imagem deste comportamento.
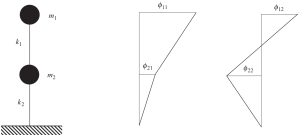
Figura nº 9. Análise de frequência mostrando os resultados dos dois autovetores. (Tigela, 2017, Página 135)
SkyCiv Structural 3D
Execute análises de frequência para suas estruturas com SkyCiv Structural 3D. Inscreva-se hoje para começar!
Referências:
- Eduardo Kausel, (2017). “Dinâmica Estrutural Avançada” 1ª edição, Cambridge University Press


