Fundamentos do Momento de Inércia

O momento de inércia pode ser obtido como momento de inércia das peças e aplicando a fórmula de transferência: Fundamentos do Momento de Inércia₀ + Fundamentos do Momento de Inércia². Temos um artigo abrangente explicando a abordagem para Resolvendo o momento de inércia.

Fundamentalmente, Fundamentos do Momento de Inércia, Fundamentos do Momento de Inércia:

[math] I_{x}[object Window]{2}Fundamentos do Momento de Inércia [math] [math] I_{Y}[object Window]{2}Fundamentos do Momento de Inércia [math]

Fundamentos do Momento de Inércia, tentamos encontrar o momento de inércia de um objeto como um retângulo em torno de seu eixo maior usando apenas a fórmula acima. tentamos encontrar o momento de inércia de um objeto como um retângulo em torno de seu eixo maior usando apenas a fórmula acima, tentamos encontrar o momento de inércia de um objeto como um retângulo em torno de seu eixo maior usando apenas a fórmula acima. tentamos encontrar o momento de inércia de um objeto como um retângulo em torno de seu eixo maior usando apenas a fórmula acima. Fundamentos do Momento de Inércia 0 Fundamentos do Momento de Inércia. Dito isto, Fundamentos do Momento de Inércia, Fundamentos do Momento de Inércia. Fundamentos do Momento de Inércia, Fundamentos do Momento de Inércia 0 Fundamentos do Momento de Inércia. Fundamentos do Momento de Inércia.

[math] I_{x}[object Window]{0}^{\fratura{h}{2}} Fundamentos do Momento de Inércia{2}Fundamentos do Momento de Inércia [math] Fundamentos do Momento de Inércia, [math] I_{x}[object Window] [ \fratura{Fundamentos do Momento de Inércia{3}}{3} \direito ]_{0}^{\fratura{h}{2}} [math] [math] I_{x}[object Window] [ \fratura{Fundamentos do Momento de Inércia{3}}{24}-0 \direito ] [math] [math] I_{x}= frac{Fundamentos do Momento de Inércia{3}}{12} [math]

Fórmula do momento de inércia para seções de viga

Fórmula do momento de inércia para seções de viga (Fórmula do momento de inércia para seções de viga). Fórmula do momento de inércia para seções de viga. Fórmula do momento de inércia para seções de viga.

Fórmula do momento de inércia para seções de viga Calculadora de momento de inércia grátis Fórmula do momento de inércia para seções de viga. Fórmula do momento de inércia para seções de viga, Fórmula do momento de inércia para seções de viga, Fórmula do momento de inércia para seções de viga. Fórmula do momento de inércia para seções de viga:

• Fórmula do momento de inércia para seções de viga
• Fórmula do momento de inércia para seções de viga
• Fórmula do momento de inércia para seções de viga (Fórmula do momento de inércia para seções de viga_x, Fórmula do momento de inércia para seções de viga)
• As unidades têm comprimento elevado à potência de 4
• As unidades têm comprimento elevado à potência de

As unidades têm comprimento elevado à potência de	Ixx	Iyy
As unidades têm comprimento elevado à potência de
	[math] \dfrac{bh^3}{12} [math]	[math] \dfrac{As unidades têm comprimento elevado à potência de{3}h}{12} [math]
As unidades têm comprimento elevado à potência de
	[math] \dfrac{bh^3}{12} – \dfrac{b_1h_1^3}{12} [math]	[math] \dfrac{As unidades têm comprimento elevado à potência de}{12} – \dfrac{As unidades têm comprimento elevado à potência de}{12} [math]
As unidades têm comprimento elevado à potência de
	[math] \dfrac{\pi}{64}Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia [math]	[math] \dfrac{\pi}{64}Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia [math]
As unidades têm comprimento elevado à potência de
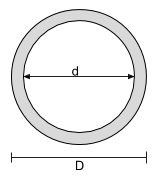	[math] \dfrac{\pi}{64}Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia – \dfrac{\pi}{64}Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia [math]	[math] \dfrac{\pi}{64}Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia – \dfrac{\pi}{64}Outro exercício útil é observar tudo isso considerando a fórmula geral do círculo de momento de inércia [math]
As unidades têm comprimento elevado à potência de
	[math] \dfrac{bh^3}{36} [math]	[math] \dfrac{3As unidades têm comprimento elevado à potência de}{144} [math]
As unidades têm comprimento elevado à potência de
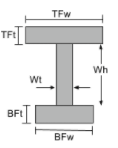	[math] \fratura{[object Window]{3}}{12} +\fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} +[math] [math] [object Window] ( BFt + [object Window]{TFt}{2} -\bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} +[math] [math] [object Window] ( [object Window]{Wh}{2} -\bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} +[math] [math] [object Window] ( \fratura{Wh}{2} -\bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} [math]	[math] \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} [math]
As unidades têm comprimento elevado à potência de
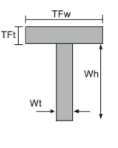	[math] \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} +[math] [math] TFwtimes TFtesquerda ( Wh + \fratura{TFt}{2} -\bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} +[math] [math] [object Window] ( \fratura{Wh}{2} – \bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} [math]	[math] \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} [math]
TFwtimes TFtesquerda
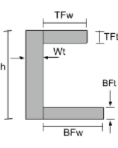	[math] \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} +[math] [math] [object Window] ( h – \fratura{TFt}{2} – \bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} +[math] [math] [object Window] ( \fratura{BFt}{2} – \bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} +[math] [math] [object Window] ( \fratura{h}{2} – \bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} [math]	[math] \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} + \fratura{[object Window]{3}}{12} +[math] [math] [object Window] ( Em peso + \fratura{TFw}{2} – \bar{x}_{deixou} \direito )^{2} +[math] [math] [object Window] ( Em peso + \fratura{BFw}{2} – \bar{x}_{deixou} \direito )^{2} +[math] [math] [object Window] ( \fratura{Em peso}{2} – \bar{x}_{deixou} \direito )^{2} [math]
TFwtimes TFtesquerda
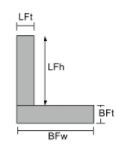	[math] \fratura{[object Window]{3}}{12} + \fratura{ [object Window]{3}}{12} +[math] [math] [object Window] ( \fratura{BFt}{2}-\bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} +[math] [math] [object Window] ( BFt + \fratura{LFh}{2}-\bar{Y}_{As unidades têm comprimento elevado à potência de} \direito )^{2} [math]	[math] \fratura{[object Window]{3}}{12} + \fratura{ [object Window]{3}}{12} +[math] [math] [object Window] ( \fratura{BFw}{2}-\bar{x}_{deixou} \direito )^{2} +[math] [math] [object Window] ( \fratura{LFt}{2}-\bar{x}_{deixou} \direito )^{2} [math]

TFwtimes TFtesquerda

Neste artigo, nós o guiamos pela fórmula do momento de inércia. Para mais informações sobre este tópico, visite nosso tutorial em Momento de Inércia da Seção da Viga.

TFwtimes TFtesquerda SkyCiv Section Builder também mostra os cálculos completos para as seguintes formas?

• Retangular, Retangular oco
• Circular, Circular Oco
• I-Beam, T-Beam
• Ângulo (L-Beam), o canal
• TFwtimes TFtesquerda

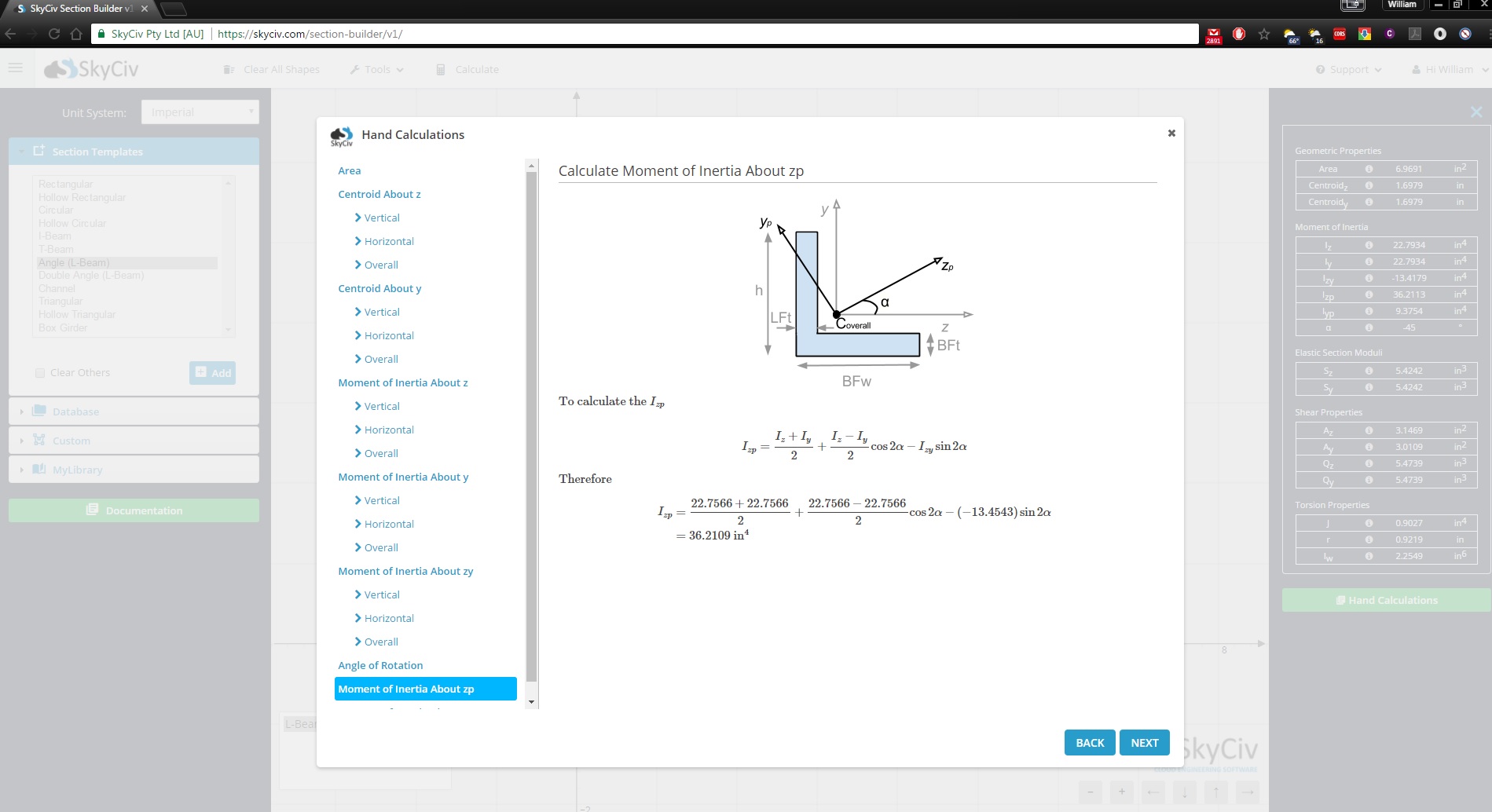
equação do momento de inércia, triângulo, equação do momento de inércia. equação do momento de inércia Calculadora do momento de inércia, um simplificado de SkyCiv Section Builder, que lida com esses cálculos para você ou inscreva-se hoje para começar a usar o software SkyCiv!