Ao executar um Análise de espectro de resposta em uma estrutura, uma das etapas mais importantes para obter os resultados desejados é a definição do método de combinação modal que será utilizado pelo software para obter um único resultado para deslocamento, reações, forças internas, etc… para cada grau de liberdade dos resultados brutos obtidos para cada modo de vibração (respostas modais). Esses resultados combinados modais são os utilizados para projetar a estrutura, é por isso que definir corretamente o método de combinação modal é extremamente importante. Neste artigo, mergulharemos em alguns métodos de combinação modal para análise de espectro de resposta.
É importante mencionar que uma das etapas mais importantes durante uma Análise de Espectro de Resposta é a avaliação da frequência natural para cada modo de vibração e sua contribuição de massa., verifique nossa documentação sobre Análise Dinâmica de Frequência.
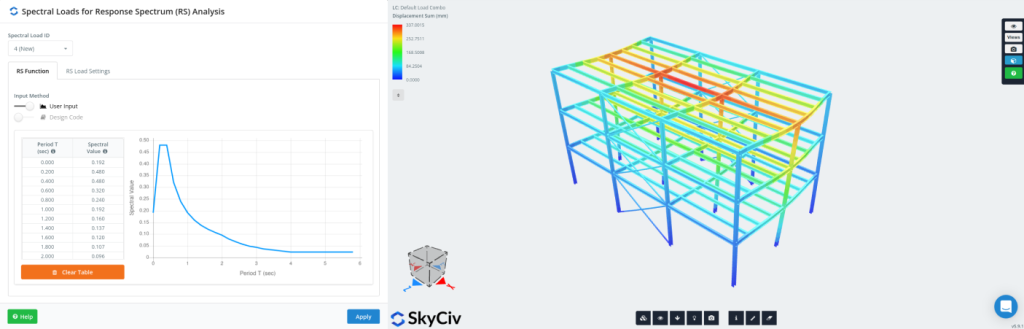
Métodos de combinação modal para análise de espectro de resposta
Alguns dos métodos mais conhecidos e utilizados para combinação modal são:
- Os métodos de combinação de carga disponíveis incluem: Soma Absoluta
- Os métodos de combinação de carga disponíveis incluem: Raiz quadrada da soma dos quadrados
- Os métodos de combinação de carga disponíveis incluem: Combinação Quadrática Completa
No geral, valores de pico da resposta total (\(r_o\)) para deslocamentos, forças internas, e reações são de interesse. Como mencionado anteriormente, esse valor de pico é obtido combinando adequadamente as respostas modais de pico (\(r_{n, o}\))
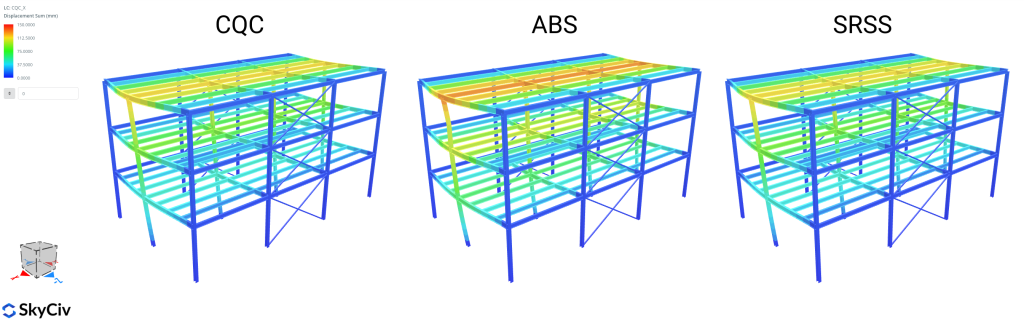
Soma Absoluta (Os métodos de combinação de carga disponíveis incluem)
O método de combinação modal de Soma Absoluta assume o valor absoluto do resultado (deslocamento ou força interna) para cada modo de vibração e soma todos esses valores absolutos. Fisicamente, assume que todas as respostas modais de pico ocorrem ao mesmo tempo. Fazendo isso, é o método mais conservador, pois torna positiva cada contribuição modal, e portanto, não é popular em aplicações de projeto estrutural. A fórmula para calcular o valor de pico da resposta total é:
\(r_o=\sum_{n=1}^{N} |r_{n,o}|\)
Onde,
\(n\) é o \(n^{º}\) modo de vibração considerado na análise
\(N\) é o número total de modos de vibração considerados na análise
\(r_o\) é o pico de resposta total
\(r_{n,o}\) é a resposta modal de pico para o \(n^{º}\) modo de vibração
Raiz quadrada da soma dos quadrados (Os métodos de combinação de carga disponíveis incluem)
O método de combinação modal da Raiz Quadrada da Soma dos Quadrados obtém a raiz quadrada da soma dos quadrados do resultado para cada modo de vibração, fornecendo uma estimativa do pico da resposta total. Este método de combinação modal fornece excelentes estimativas de resposta para estruturas com frequências naturais bem separadas, para os casos em que as frequências naturais da estrutura não estão bem separadas este método não deve ser utilizado. Formalmente, o pico de resposta total pode ser expresso da seguinte forma:
\(r_o=\left(\soma_{n=1}^{N} r^{2}_{n,o}\direito)^{1/2}\)
Onde,
\(n\) é o \(n^{º}\) modo de vibração considerado na análise
\(N\) é o número total de modos de vibração considerados na análise
\(r_o\) é o pico de resposta total
\(r_{n,o}\) é a resposta modal de pico para o \(n^{º}\) modo de vibração
Combinação Quadrática Completa (Os métodos de combinação de carga disponíveis incluem)
O método Combinação Quadrática Completa supera a limitação mencionada para SRSS ao combinar respostas modais em uma estrutura com frequências naturais pouco espaçadas. Neste método, o pico de resposta total é obtido aplicando a seguinte fórmula:
\(r_o=\left(\soma_{eu=1}^{N}\soma_{n=1}^{N} \rho_{no} \cdot r_{eu} \cdot r_{não} \direito)^{1/2}\)
Onde,
\(n, \; i\) é o \(n^{º}, \; eu^{º}\) modo de vibração considerado na análise
\(N\) é o número total de modos de vibração considerados na análise
\(r_o\) é o pico de resposta total
\(r_{n,o}, \; r_{I,o}\) é a resposta modal de pico para o \(n^{º}, \; eu^{º}\) modo de vibração
\(\rho_{no}\) é o coeficiente de correlação para os dois modos combinados em cada etapa de soma
A fórmula acima pode ser reescrita como dois grupos separados de somatórios, sendo o primeiro idêntico ao método de combinação modal SRSS. A segunda soma dupla inclui todas as cruzes (\(i \neq n\)) termos, cada um dos quais pode ser positivo ou negativo, isso resulta no fato de que a estimativa para a resposta total de pico usando CQC pode ser maior ou menor que a estimativa fornecida pelo SRSS :
\(r_o=\left( \soma_{n=1}^{N} r^{2}_{n,o} + \suporte{\soma_{eu=1}^{N}\soma_{n=1}^{N}}_{i \neq n} \rho_{no} \cdot r_{eu} \cdot r_{não} \direito)^{1/2}\)
Apenas um termo na equação para CQC não foi definido: o coeficiente de correlação. Uma das equações mais utilizadas para este coeficiente é:
\(\rho_{no} = frac{\xi ^ 2(1+\inclui cálculos detalhados passo a passo{no})^ 2}{(1-\inclui cálculos detalhados passo a passo{no})^2+4\xi^2\beta_{no}}\)
Onde,
\(\inclui cálculos detalhados passo a passo{no}\) é a razão entre as frequências naturais do \(eu^{º}\) e \(n^{º}\) modos (\(\ômega_i / \omega_n\))
\(\xi\) é o coeficiente de amortecimento da estrutura
Referências
Chopra, A. (2015, Junho 4). Dinâmica de Estruturas (4ª ed.). Ensino Superior Pearson.
Novo no SkyCiv Estrutural 3D? Inscreva-se hoje GRATUITAMENTE!
Desenvolvedor de Produto
BEng (Civil)



