Um exemplo totalmente trabalhado de AS / NZS 1170.2 (2011) cálculos de carga de vento
SkyCiv’s calculadora de carga de vento agora tem várias referências de código, incluindo os Padrões Australianos/Nova Zelândia. Neste artigo, estaremos calculando a pressão do vento do projeto para uma estrutura de armazém. Estaremos usando um modelo de nosso S3D para demonstrar como as cargas (AS 1170.2 / NZS1170.2:2011 ) são aplicados em cada superfície.
Observe que o exemplo abaixo é baseado no 2011 versão do AS/NZS 1170.2. Os procedimentos para a versão mais recente podem ser diferentes, mas ainda assim devem ser semelhantes no cálculo.
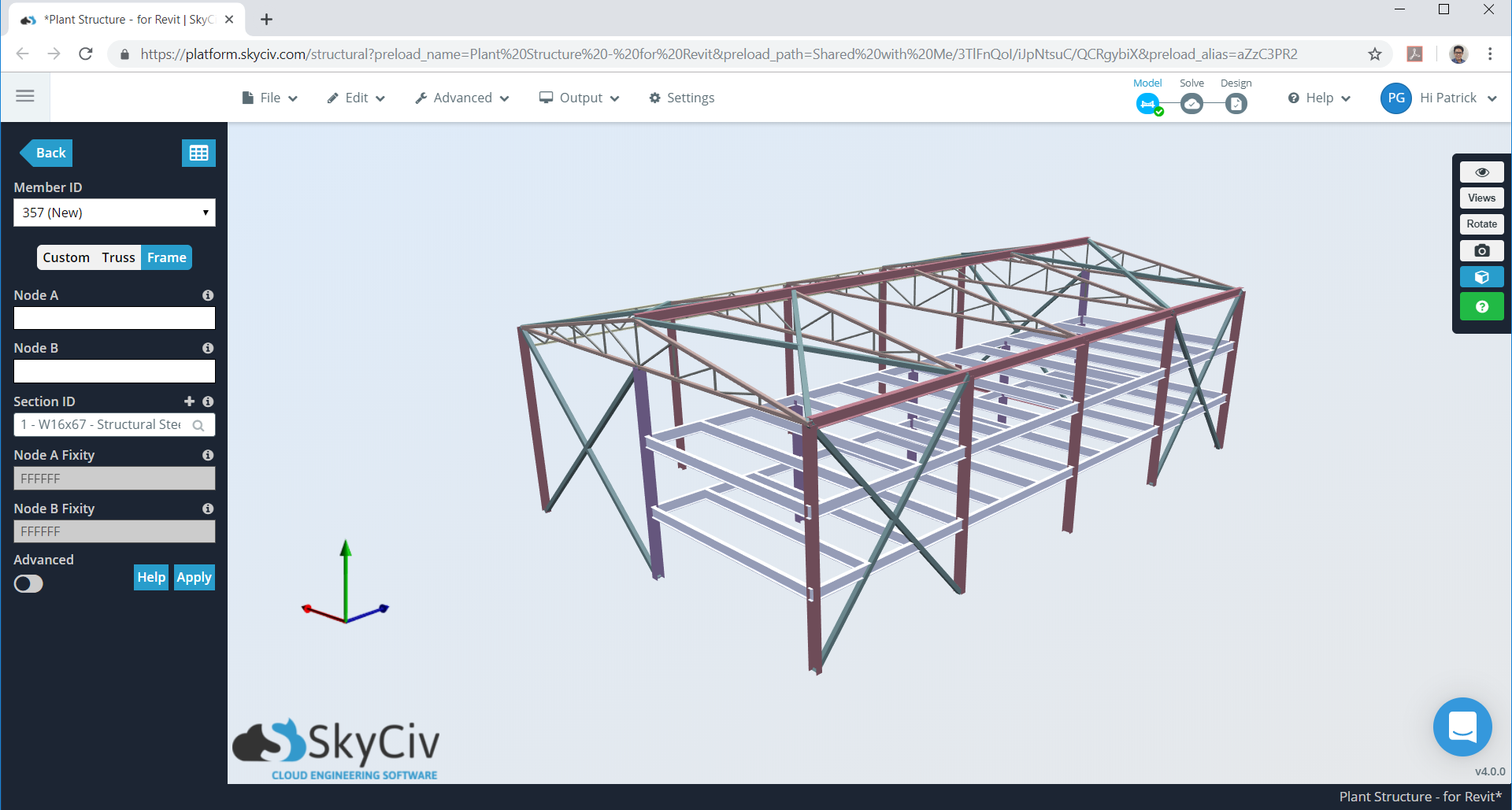
Figura 1. Modelo de armazém no SkyCiv S3D como exemplo.
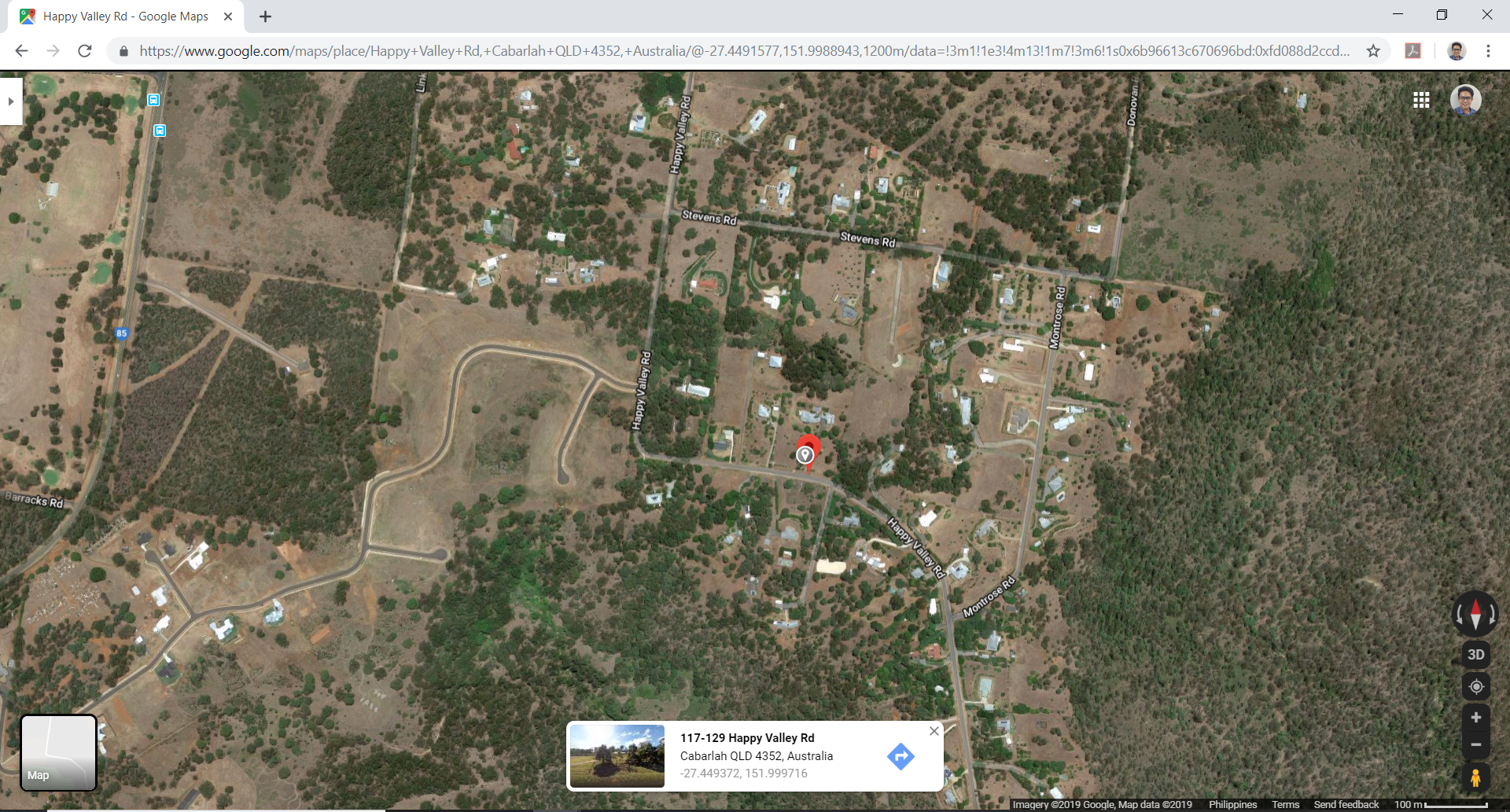
Figura 2. Localização do site (do Google Maps).
Tabela 1. Dados do edifício necessários para o cálculo de vento.
| Localização | Happy Valley Road, Desafie, Queensland, Austrália |
| Ocupação | Diversos – Estrutura do Armazém |
| Terreno | Terreno plano, agrícola |
| Dimensões | 19.507 m (L) × 31.699 m (B) No plano Altura da beirada 9.144 m Altura do ápice. 10.973 m Inclinação do telhado 3:16 (10.62°) Sem abrir |
| Revestimento | Purlins espaçados em 0.6 m Vigas de parede espaçadas em 0.6 m |
A fórmula para determinar a pressão do vento do projeto é:
Para projetar a velocidade do vento:
\({V}_{sentar,b} = {V}_{R} {M}_{d} {M}_{z,gato} {M}_{s} {M}_{t} \) (1)
Onde:
\({V}_{sentar,b}\) = velocidade do vento projetada em m / s
\({V}_{R}\) = velocidade do vento de rajada 3s regional (do mapa do vento), em (AS / NZS 1170.2 Seção 3)
\({M}_{d}\)= multiplicador direcional do vento para 8 direções cardinais (b) (AS / NZS 1170.2 Seção 3)
\({M}_{z,gato}\) = terreno / multiplicador de altura (AS / NZS 1170.2 Seção 4)
\({M}_{s}\)= multiplicador de blindagem, definido como 1.0 (AS / NZS 1170.2 Seção 4)
\({M}_{t}\)= multiplicador topográfico (AS / NZS 1170.2 Seção 3)
Para projetar a pressão do vento:
\(p = 0.5 {⍴}_{ar} ({V}_{de,θ})^ 2 {C}_{FIG} {C}_{homem} \) (2)
Onde:
\(p ) = pressão do vento projetada em Pa
\({⍴}_{ar}\) = densidade do ar (1.2 kg / cu.m.)
\({V}_{de,θ}\)= velocidade do vento de desenho ortogonal do edifício
\({C}_{homem}\)= fator de resposta dinâmica, definido como 1.0
\({C}_{FIG}\) = fator de forma aerodinâmica (para pressão interna ou externa) para edifícios fechados onde:
\({C}_{FIG,I} = {C}_{p,I} {K}_{c,I} \) – para pressões internas (3)
\({C}_{FIG,e} = {C}_{p,e} {K}_{uma} {K}_{c,e} {K}_{eu} {K}_{p}\) – para pressões externas (4)
\({C}_{p,I}\) = coeficiente de pressão interna
\({K}_{c,I}\) = fator de combinação aplicado às pressões internas
\({C}_{p,e}\) = coeficiente de pressão externa
\({K}_{uma}\) = fator de redução de área
\({K}_{c,e}\) = fator de combinação aplicado a pressões externas
\({K}_{eu}\) = fator de pressão local
\({K}_{p}\) = fator de revestimento poroso
Cada parâmetro será discutido posteriormente.
Velocidade do vento regional, \({V}_{R}\)
Os dados regionais de velocidade do vento são detalhados na figura 3.1 do AS / NZS 1170.2 (como mostrado nas figuras 3 e 4 abaixo). Cada área administrativa é classificada em regiões de velocidade do vento com a velocidade do vento correspondente. Para nosso exemplo, o site está localizado perto do ponto vermelho e é classificado como Região A4 uma vez que é aproximadamente 106 km da suavizada costa da ilha principal da Austrália. A velocidade do vento correspondente pode ser calculada usando a tabela 3.1 de AS / NZS 1170.2 como mostrado na figura 5. O intervalo de recorrência anual é selecionado dependendo do nível de importância e da vida útil do projeto da estrutura, conforme detalhado na Tabela 3.3 de AS / NZS 1170.0.
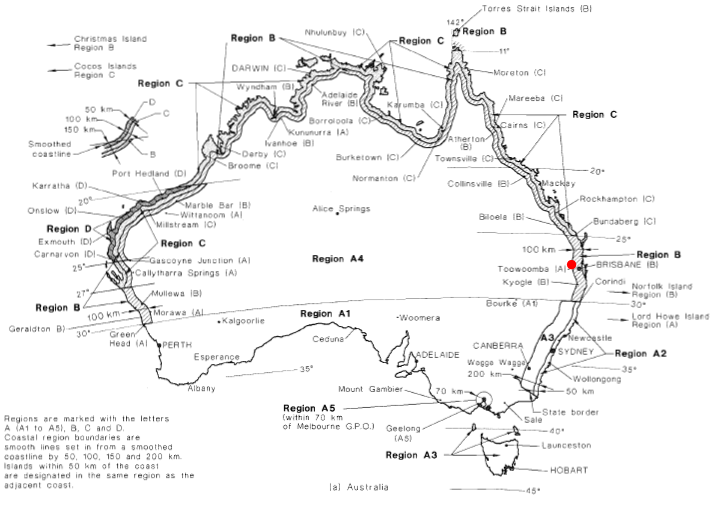
Figura 3. Mapa regional da velocidade do vento para a Austrália (Figura 3.1(A) de AS / NZS 1170.2).
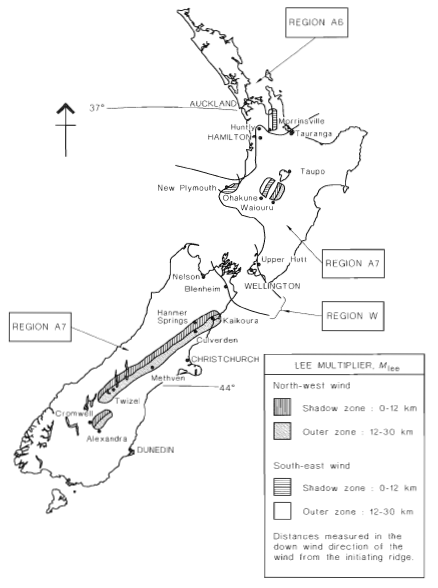
Figura 4. Mapa regional de velocidade do vento para a Nova Zelândia (Figura 3.1(B) de AS / NZS 1170.2).
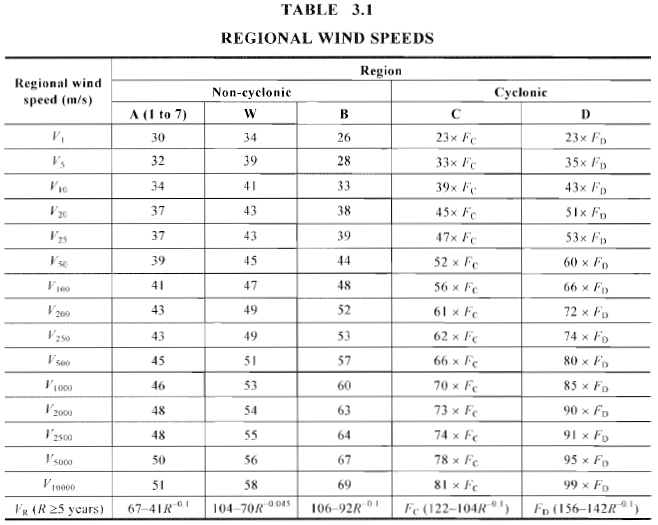
Figura 5. Velocidade do vento correspondente com base na região do vento e intervalo de recorrência anual (Tabela 3.1 de AS / NZS 1170.2).
Para estados limites finais ou de manutenção, Mesas 3.1 e 3.3 de AS / NZS 1170.0 (Figuras 6 e 7) detalha como classificar a estrutura por nível de importância e sua probabilidade anual de excedência correspondente.
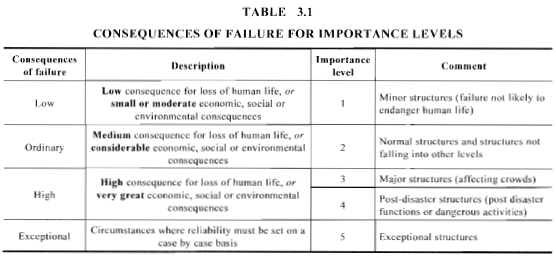
Figura 6. Definição do nível de importância de acordo com a Tabela 3.1 de AS / NZS 1170.0.
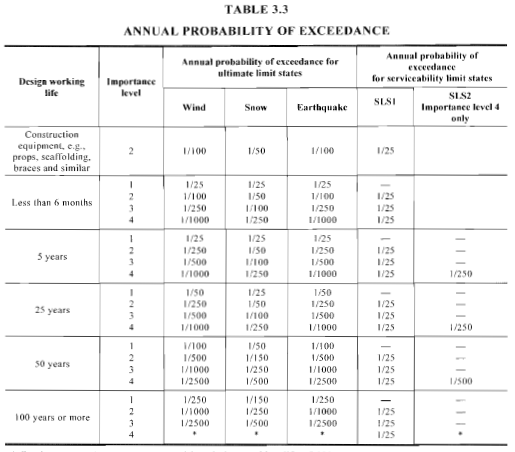
Figura 7. Definição da probabilidade anual de superação de acordo com a Tabela 3.3 de AS / NZS 1170.0.
Para nosso exemplo, devemos apenas considerar o estado limite final. Nossa estrutura de exemplo é classificada como “Ordinário” e assumiu ter uma vida útil de projeto de 50 anos. Conseqüentemente, devemos adotar a probabilidade anual de excedência equivalente a 1/500. Conseqüentemente, o valor correspondente do nosso \({V}_{R}\) é 45 em.
SkyCiv agora automatiza a detecção da região do vento e obtém o valor da velocidade do vento correspondente com apenas algumas entradas. Tentar nosso SkyCiv Free Wind Tool
Multiplicador de direção do vento, \({M}_{d}\)
Para cada região de vento e a direção correspondente do vento (8 direções cardinais), multiplicador da direção do vento, \({M}_{d}\), são diferentes em valores, conforme mostrado na Tabela 3.2 de AS / NZS 1170.2.
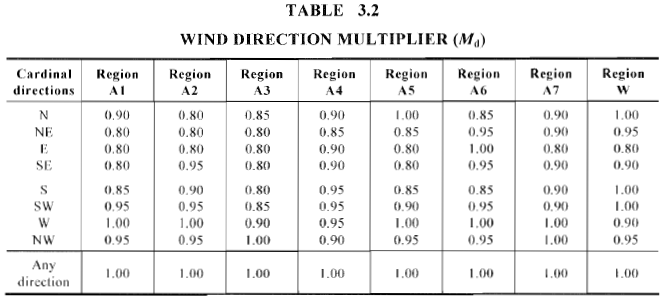
Figura 8. Valores do multiplicador de direção do vento por região e direção do vento de acordo com a Tabela 3.2 de AS / NZS 1170.2.
Para este exemplo, devemos verificar a velocidade do vento vindo de “NASCIDO” no qual \({M}_{d}\) = 0.85. Contudo, também é seguro assumir \({M}_{d}\) = 1.0 para dar um resultado conservador.
Multiplicador de terreno / altura, \({M}_{z,gato}\)
Para calcular o multiplicador de terreno / altura \({M}_{z,gato}\), precisamos classificar a categoria de terreno do nosso site. Tabela 2 mostra a definição de cada categoria de terreno com base na seção 4.2.1 de AS / NZS 1170.2. \({M}_{z,gato}\) agora pode ser calculado usando a Tabela 4.1 de AS / NZS 1170.2 dependendo da altura, região do vento e categoria de terreno da estrutura.
Tabela 2. Definição de categoria de terreno para AS / NZS 1170.2.
| Categoria de Terreno | Definição |
|---|---|
| Categoria 1 | Terreno aberto exposto com poucas ou nenhuma obstrução e superfícies de água em velocidades de vento de manutenção |
| Categoria 2 | Superfícies de água, terreno aberto, pastagem com poucos, obstruções bem espalhadas com alturas geralmente de 1.5 ma 10m |
| Categoria 3 | Terreno com numerosas obstruções espaçadas 3 m para 5 m alto, como áreas de habitação suburbana. |
| Categoria 4 | Terreno com numerosos grandes, Alto (10 m para 30 m alto) e obstruções espaçadas, como grandes centros de cidades e complexos industriais bem desenvolvidos. |
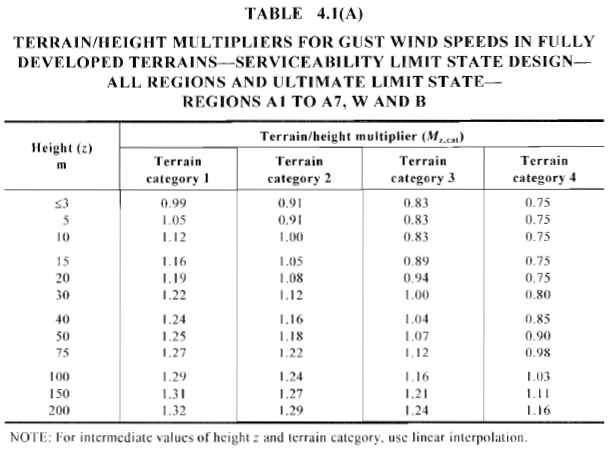
Figura 9. Multiplicador Calculado de Terreno / Altura, \({M}_{z,gato}\) , com base na categoria de terreno correspondente e região de vento (Tabela 4.1 de AS / NZS 1170.2).
Para nosso exemplo, a localização do site pode ser classificada como “Categoria 2” assumindo que temos uma categoria de terreno uniforme para cada direção do vento. Vamos dividir a altura da estrutura para cada 3m e a altura média do telhado. Os valores tabulados de \({M}_{z,gato}\) para cada nível é mostrado na Tabela 3.
Tabela 3. Calculado \({M}_{z,gato}\) para cada nível da estrutura.
| Altura, m | \({M}_{z,gato}\) |
|---|---|
| 3 m | 0.91 |
| 6 m | 0.928 |
| 9 m | 0.982 |
| 10.06 m | 1.001 |
Multiplicador de blindagem, \({M}_{s}\)
O efeito de proteção pode ser considerado no cálculo das pressões do vento de projeto usando AS / NZS 1170.2. Isso é para considerar a diminuição da pressão do vento quando estruturas próximas estão presentes. Seção 4.3 de AS / NZS 1170.2 detalha o cálculo do fator de proteção \({M}_{s}\). Para este exemplo, uma vez que a localização do site está situada em um campo aberto, e estruturas próximas têm distâncias superiores a 20h (201.2 m) da estrutura, podemos assumir o \({M}_{s}\) = 1.0.
Multiplicador Topográfico, \({M}_{t}\)
O efeito da topografia na pressão do vento é capturado no multiplicador topográfico, \({M}_{t}\), onde amplifica a pressão do vento projetada com base na elevação do solo do local, se a estrutura está em uma colina ou escarpa. Seção 4.4 do AS / NZS 1170.2 detalha o cálculo deste parâmetro. Fora da zona topográfica local, uma distância calculada do pico da colina ou escarpa, a \({M}_{t}\) pode ser considerado igual a 1.0 como mostrado nas figuras 4.2 e 4.3 de AS / NZS 1170.2 (Figura 10).
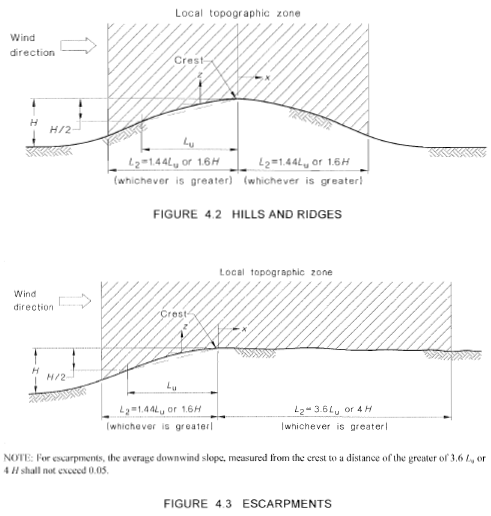
Figura 10. Parâmetros necessários para calcular o fator topográfico, \({M}_{t}\) , baseado na seção 4.4 de AS / NZS 1170.2.
A partir dos dados de elevação do solo do local (do Google Maps, vindo de NE), deduzimos que a topografia pode ser classificada como colina. Com base na Figura 4.2 de AS / NZS 1170.2, os seguintes pontos podem ser obtidos conforme mostrado na Tabela 4:
Tabela 4. Pontos de dados extraídos de dados de elevação do solo (do Google Maps) como mostrado na figura 11.
| Parâmetro | Valor |
| Mt | 1.076 |
| inclinação | 0.07 |
| Localização do pico | -380.00 m da localização da estrutura |
| Elevação do pico | 628.16 m |
| Localização do pé | -2000.00 m da localização da estrutura |
| Elevação do pé | 515.37 m |
| H | 112.79 m |
| Lugar. de H / 2 | -1154.23 m da localização da estrutura |
| x | 380.00 m |
| Lvocê | 774.23 m |
| L1 | 278.72 m |
| L2 | 1114.89 m |
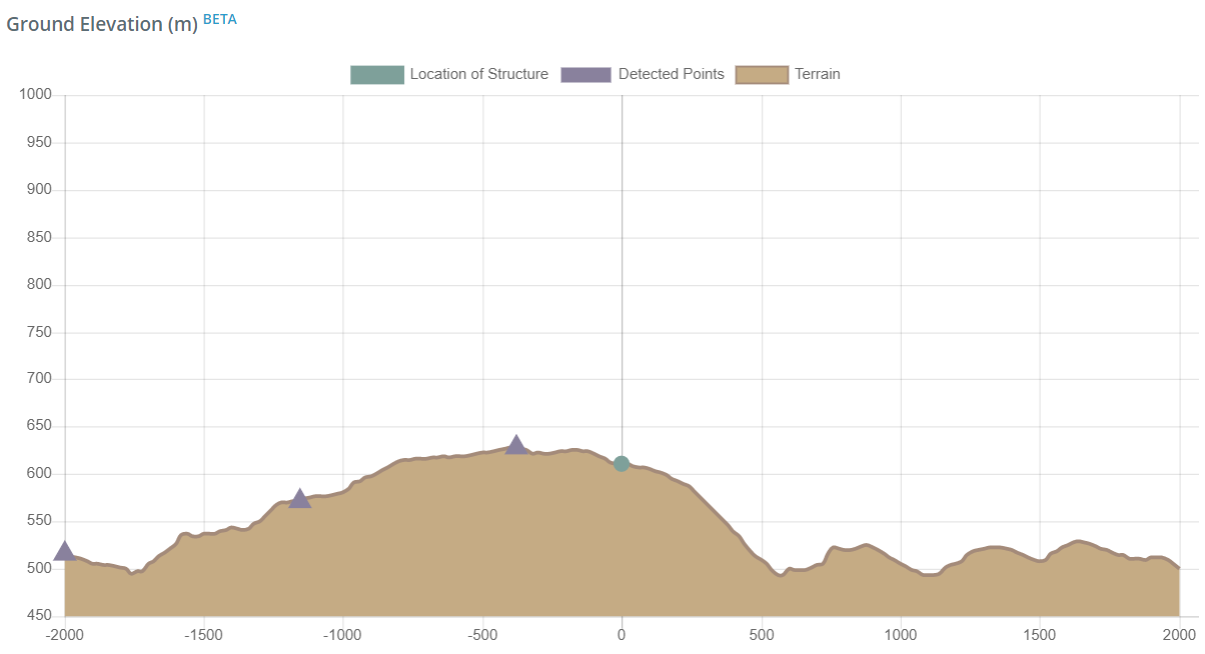
Figura 11. Elevação do solo do local na seção NE-SW (do Google Maps).
A partir dos dados mostrados na Tabela 4, o multiplicador topográfico calculado, \({M}_{t}\), é igual a 1.08 baseado na equação 4.4(2) de AS / NZS 1170.2 como mostrado na Equação (5).
\({M}_{t} = {M}_{h} = 1 + [ H / 3.5(z + {L}_{1})] [ 1 – ( |x| / {L}_{2})] \) (5)
\({M}_{t} = 1.08 \)
Finalmente, usando equação (1), a velocidade do vento de projeto calculada é mostrada na Tabela 5.
Tabela 5. Calculado \({V}_{sentar,b}\) para cada nível da estrutura.
| Altura, m | \({V}_{sentar,b}\), em |
| 3 | 37.45 |
| 6 | 38.19 |
| 9 | 40.42 |
| 10.06 | 41.20 |
Onde:
\({V}_{sentar,b (mínimo)}\) = 30 m/s para estruturas permanentes.
A fim de calcular as pressões do vento de projeto, os fatores de forma aerodinâmica, \({C}_{FIG}\), para superfícies internas e externas são necessárias. Isso será discutido na próxima seção.
Fator de forma aerodinâmica, \({C}_{FIG}\)
O fator de forma aerodinâmica, \({C}_{FIG}\), é usado para determinar os valores da pressão do vento aplicada a cada superfície. Um valor positivo de \({C}_{FIG}\) significa que a pressão está agindo em direção à superfície, enquanto negativo significa agindo longe da superfície.
Fator de forma aerodinâmica para pressão interna, \({C}_{FIG,I}\)
Coeficiente de pressão interna, \({C}_{p,I}\)
Pra \({C}_{FIG,I}\), o cálculo do coeficiente de pressão interna \({C}_{p,I}\) é detalhado na Tabela 5.1 de AS / NZS 1170.2 como mostrado na figura 12.
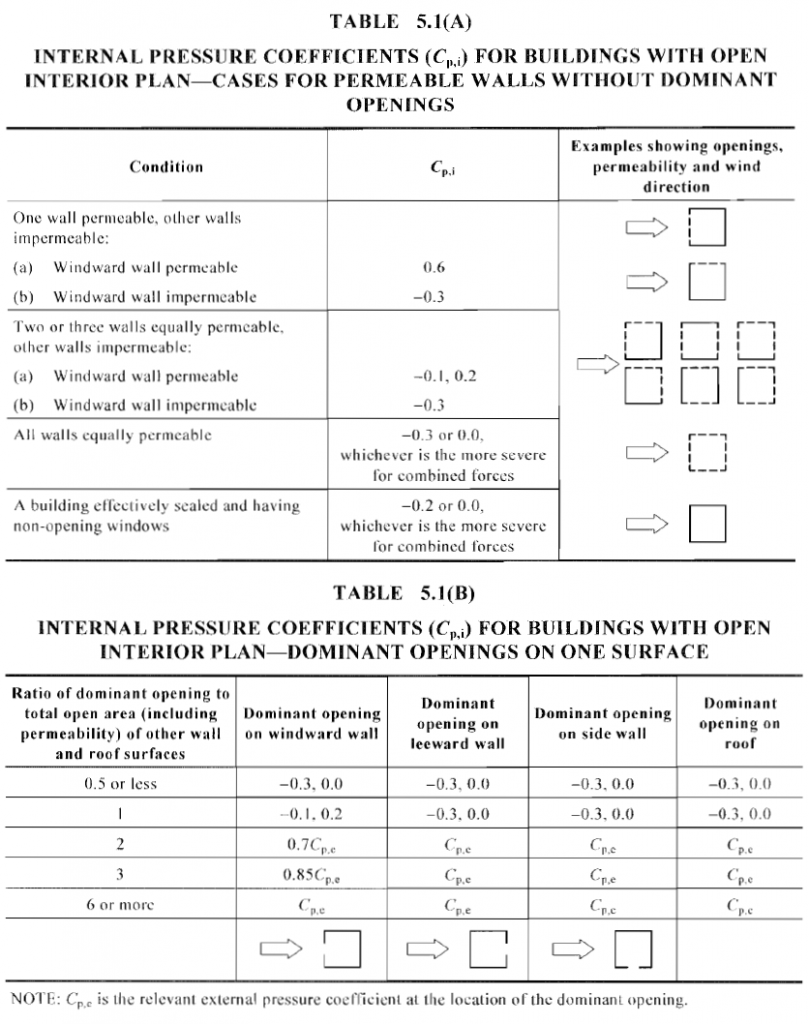
Figura 12. Coeficiente de pressão interna, \({C}_{p,I}\), conforme definido na Seção 5.3 de AS / NZS 1170.2.
Para este exemplo, nossa estrutura é fechada e presume-se que não tem abertura, por isso, a condição apropriada para esta estrutura é “Um edifício dimensionado de forma eficaz e com janelas que não abrem” e os coeficientes de pressão interna correspondentes são \({C}_{p,I}\) = -0.2, 0.0.
Fator de forma aerodinâmica para pressão externa, \({C}_{FIG,e}\)
Coeficiente de pressão externa, \({C}_{p,e}\)
Seção 5.4 de AS / NZS 1170.2 define o procedimento para obter o coeficiente de pressão externa, \({C}_{p,e}\), para edifícios retangulares. As superfícies de construção para distribuição de pressão externa são definidas na Figura 5.2 do código como mostrado se a Figura 13. Além disso, Mesas 5.2 para 5.3 de AS / NZS 1170.2 detalha os valores calculados de \({C}_{p,e}\) para cada definição de superfície, conforme mostrado nas Figuras 14 para 18.
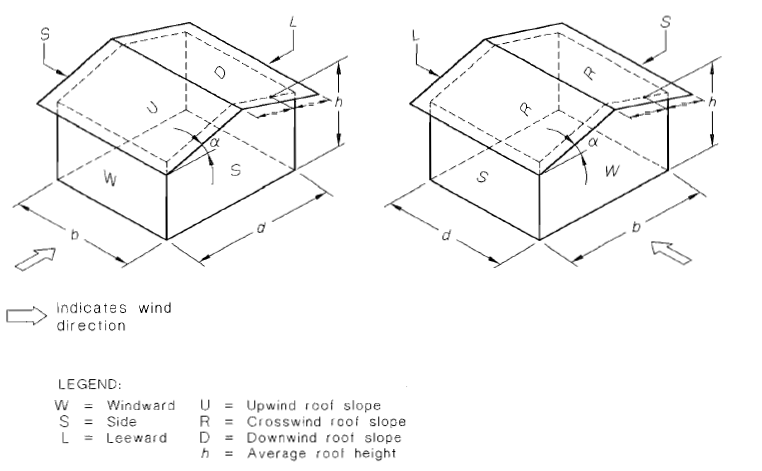
Figura 13. Definição de superfície para distribuição de pressão externa, conforme definido na Seção 5.4 de AS / NZS 1170.2.
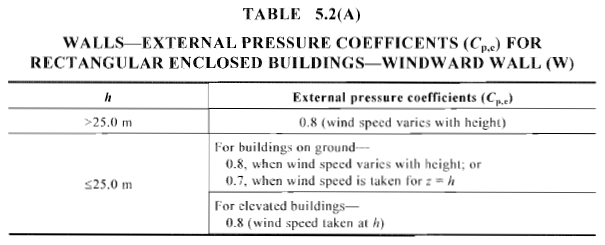
Figura 14. Coeficiente de pressão externa calculado, \({C}_{p,e}\), para parede de barlavento de edifícios fechados retangulares (Tabela 5.2(A) de AS / NZS 1170.2).
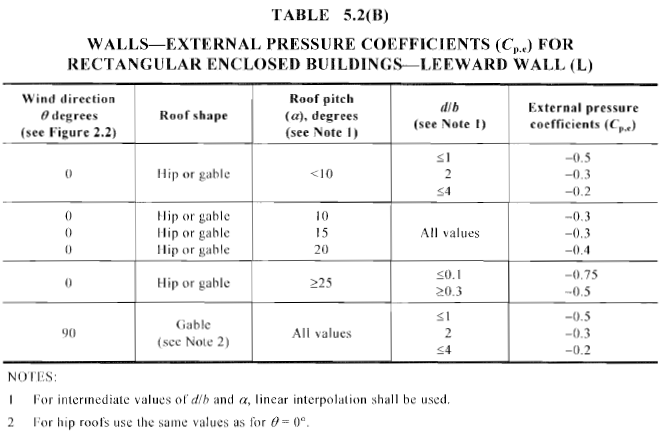
Figura 15. Coeficiente de pressão externa calculado, \({C}_{p,e}\), para parede de sotavento de edifícios retangulares fechados (Tabela 5.2(B) de AS / NZS 1170.2).
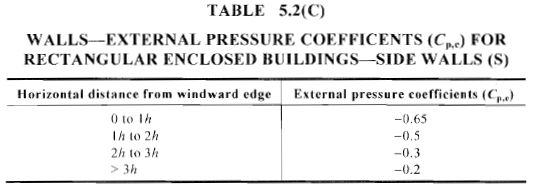
Figura 16. Coeficiente de pressão externa calculado, \({C}_{p,e}\), para paredes laterais de edifícios fechados retangulares (Tabela 5.2(C) de AS / NZS 1170.2).
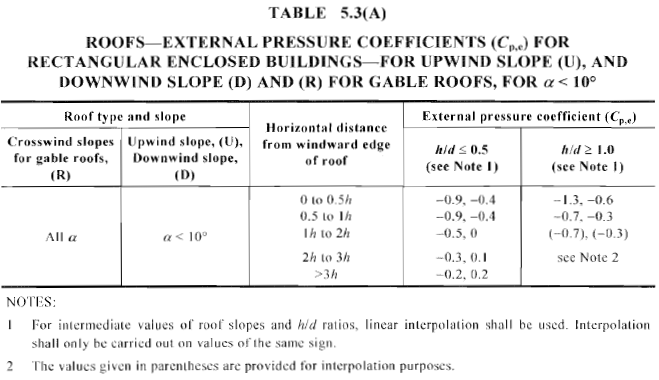
Figura 17. Coeficiente de pressão externa calculado, \({C}_{p,e}\), para superfície contra o vento e a favor do vento do telhado de duas águas com ângulo de inclinação < 10° (Tabela 5.3(A) de AS / NZS 1170.2).
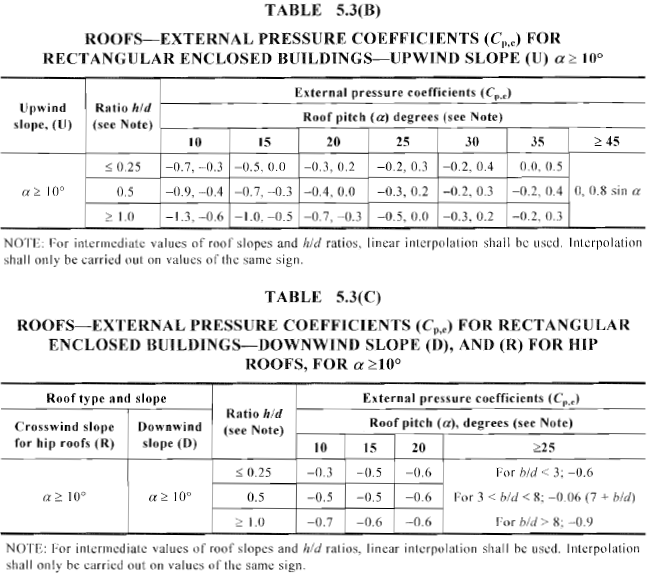
Figura 18. Coeficiente de pressão externa calculado, \({C}_{p,e}\), para superfície a favor e contra o vento de empena e telhado de quadril com ângulo de inclinação ≥ 10° (Tabela 5.3(A) e mesa 5.3(B) de AS / NZS 1170.2).
Para este exemplo, \({C}_{p,e}\) valores para superfícies de parede são mostrados na Tabela 6 e 7 abaixo de onde \(d/b\) = 0.616 para 0° e \(b / d ) = 1.625 para 90° , \(h / d ) = 0.516, e \(h/b\) = 0.317 . Além disso, Tabela 8 mostra o \({C}_{p,e}\) valores para superfícies de telhado.
Tabela 6. Coeficientes de pressão externa calculados, \({C}_{p,e}\), para superfícies de parede a barlavento e sotavento.
| Altura, m | \({C}_{p,e}\) (barlavento) | \({C}_{p,e}\) (sotavento) - ao longo de L (0°) |
\({C}_{p,e}\) (sotavento) - ao longo de B (90°) |
| 3 | 0.8 | -0.3 | -0.375 |
| 6 | 0.8 | ||
| 9 | 0.8 | ||
| 10.06 | 0.7 |
Tabela 7. Coeficientes de pressão externa calculados, \({C}_{p,e}\), para superfícies de parede lateral.
| Localização da parede de barlavento, m | \({C}_{p,e}\) (parede lateral) |
| 0 a 10,06m | -0.65 |
| 10.06 para 19.507 m | -0.50 |
Tabela 8. Coeficientes de pressão externa calculados, \({C}_{p,e}\), para superfícies de telhado.
| Superfície do telhado | \({C}_{p,e}\) |
| Contra o vento | -0.888, -0.394 |
| A favor do vento | -0.503 |
| Crosswind | -0.9, -0.4 (0 para h) -0.5, 0.0 (h a 2h) -0.3, 0.1 (2h a 3h) -0.2, 0.2 (> 3h) |
Fator de Redução de Área, \({K}_{uma}\)
Fator de redução de área, \({K}_{uma}\), é aplicável apenas a paredes laterais e superfícies de telhado. Calculado de outra forma, \({K}_{uma}\) é sempre igual a 1.0. Tabela 5.4 de AS / NZS 1170.2 mostra o valor de \({K}_{uma}\) dependendo da área de contribuição para as paredes laterais e as superfícies do telhado, conforme mostrado na Figura 19.

Figura 19. Valores do fator de redução de área, \({K}_{uma}\), para paredes laterais e superfícies de telhado (Tabela 5.4 de AS / NZS 1170.2).
Para nosso exemplo, os valores calculados do fator de redução de área são mostrados na Tabela 9 abaixo.
Tabela 9. Valores do fator de redução de área, \({K}_{uma}\), para este exemplo.
| Superfície | Área, m2. | \({K}_{uma}\) |
| parede lateral (ao longo d) | 196.21 | 0.8 |
| parede lateral (ao longo de b) | 285.29 | 0.8 |
| cobertura – barlavento | 314.564 | 0.8 |
| cobertura – sotavento | 314.564 | 0.8 |
| cobertura – vento cruzado | 629.129 | 0.8 |
Fator de pressão local para revestimentos, \({K}_{eu}\)
O fator de pressão local, \({K}_{eu}\), é sempre igual a 1.0 para todas as superfícies, exceto para componentes e revestimentos. Seção 5.4.4 de AS / NZS 1170.2 detalha o procedimento de cálculo para obter \({K}_{eu}\) para esses componentes.
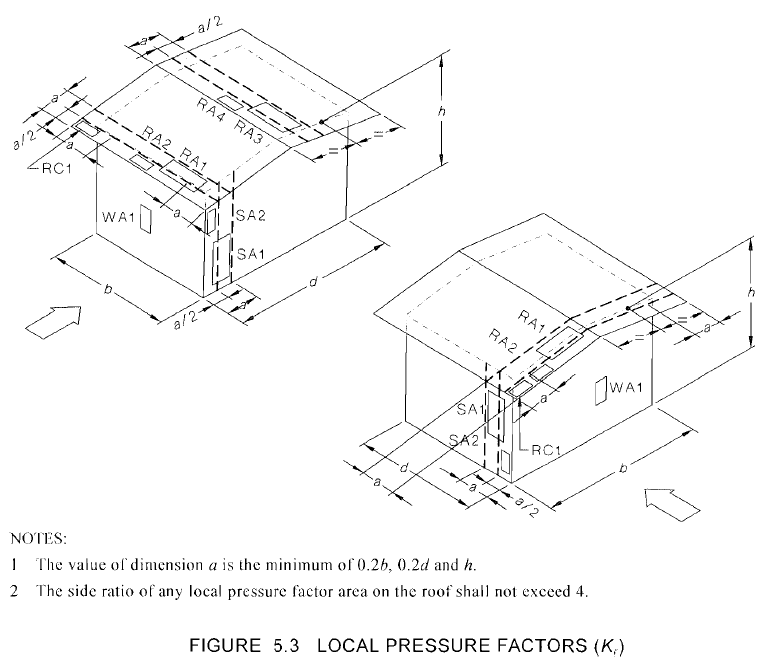
Figura 20. Localização das pressões de revestimento conforme definido na Tabela 5.6 de AS / NZS 1170.2.
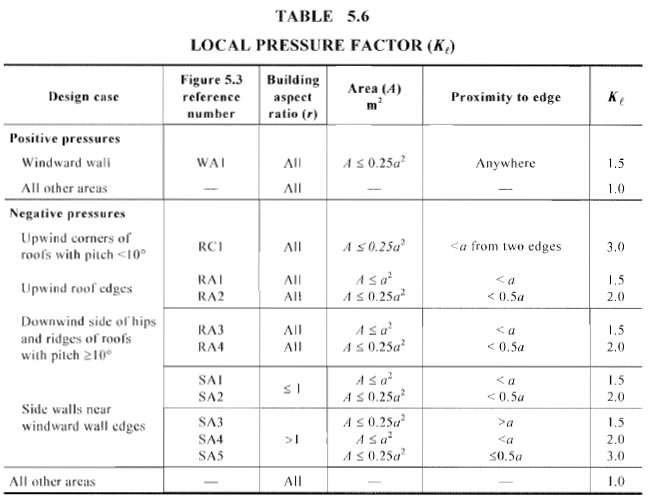
Figura 21. Valores do fator de pressão local, \({K}_{eu}\), para cada zona, conforme mostrado na Figura 20.
Para este exemplo, os valores de \(uma) é o mínimo de \(0.2b\) (3.91 m), \(02.d\) (6.34 m), ou \(h ) (10.06m), por isso, \(uma) = 3.91 m. A área correspondente e o fator de pressão local para terças e vigas de parede são mostrados na Tabela 10 abaixo com a suposição de que o comprimento do vão da madre é igual ao espaçamento das treliças (7.924 m) e o comprimento do vão das vigas da parede é igual à altura da história (3 m). A proporção do edifício é a maior de \(h / d ) (0.516) e \(h/b\) (0.317).
Tabela 10. Valores do fator de pressão local \({K}_{eu}\) para terças e pregos de parede.
| Revestimento | Área, m2. | Zonas | Kl para pressão positiva | Kl para pressão negativa |
| madre | 4.75 | RA1 | 1.0 | 1.5 |
| RA3 | 1.0 | 1.5 | ||
| pregos de parede | 1.80 | WA1 | 1.0 | 1.0 |
| SA1 | 1.0 | 1.5 | ||
| SA2 | 1.0 | 2.0 |
Fator de redução de revestimento permeável, \({K}_{p}\), para telhados e paredes laterais
O fator de redução do revestimento permeável, \({K}_{p}\), é sempre igual a 1.0 a todas as superfícies, exceto que uma superfície externa consiste em revestimento permeável e a razão de solidez é menor que 0.999 onde a proporção de solidez é a proporção da área sólida para a área de superfície total. Para este exemplo, devemos assumir que \({K}_{p}\) é igual a 1.0.
Fatores de combinação de ação, \({K}_{c,I}\) e \({K}_{c,e}\)
Fatores de combinação de ação, \({K}_{c,I}\) e \({K}_{c,e}\), são usados para calcular o efeito da carga do vento agindo simultaneamente em superfícies específicas (como o vento agindo nas paredes, telhados, e pressões internas). Tabela 5.5 do AS / NZS 1170.2 mostra exemplos de combinação de ação com seus fatores de combinação de ação correspondentes, conforme ilustrado na Figura 22.
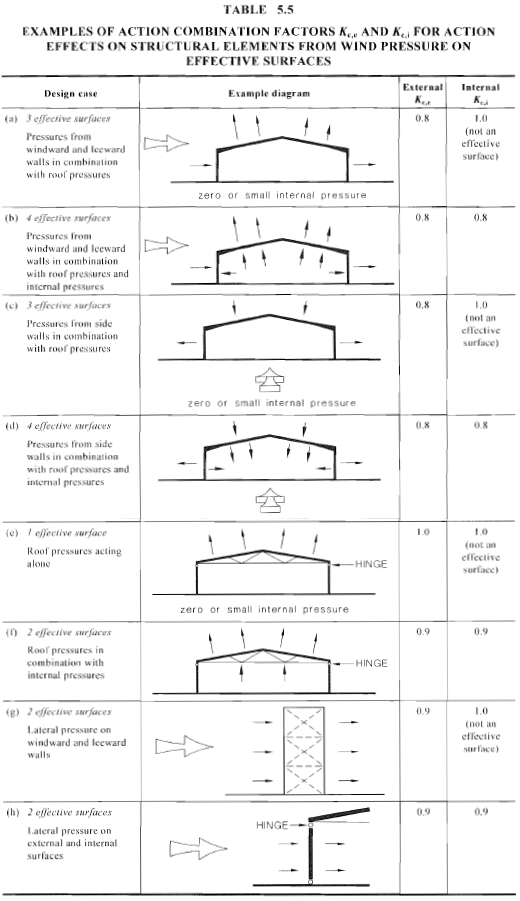
Figura 22. Fatores de combinação de ação \({K}_{c,e}\) e \({K}_{c,I}\) da mesa 5.5 de AS / NZS 1170.2.
Para este exemplo, devemos considerar o caso de design (b) Onde 4 superfícies eficazes são carregadas com as pressões de design. Conseqüentemente, \({K}_{c,I}\) e \({K}_{c,e}\) são ambos iguais a 0.8.
Projetar as pressões do vento para a estrutura principal
Uma vez que já temos os parâmetros necessários, \(p ), podemos obter os valores de pressão do vento do projeto usando as Equações (2) para (4). Mesas 11 para 13 mostrar o resumo dos parâmetros para cada superfície.
Tabela 11. Valores de pressão de projeto para parede de barlavento.
| altura, m | \({M}_{z,gato}\) | \({V}_{de,θ}\) | \({C}_{FIG}\) | \({C}_{p,e}\) | \({K}_{uma}\) | \({K}_{c,e}\) | \({K}_{eu}\) | \({K}_{p}\) | Pressão de Design \(p ), Nós vamos |
| 3 | 0.910 | 37.45 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 538.64 |
| 6 | 0.928 | 38.19 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 560.16 |
| 9 | 0.982 | 40.42 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 627.25 |
| 10.06 | 1.001 | 41.20 | 0.560 | 0.7 | 1 | 0.8 | 1 | 1 | 570.29 |
Tabela 12. Valores de pressão de projeto calculados para sotavento e paredes laterais, e superfícies de telhado.
| Superfície | \({V}_{de,θ}\) | \({C}_{FIG}\) | \({C}_{p,e}\) | \({K}_{uma}\) | \({K}_{c,e}\) | \({K}_{eu}\) | \({K}_{p}\) | Pressão de Design \(p ), Nós vamos |
| Parede de sotavento | 41.20 | -0.24 | -0.3 | 1 | 0.8 | 1 | 1 | -244.41 |
| Parede lateral (0 a 10,06m) |
-0.520* | -0.65 | 0.8 | 0.8 | 1 | 1 | -529.55 | |
| Parede lateral (0 a 10,06m) |
-0.400* | -0.5 | 0.8 | 0.8 | 1 | 1 | -407.35 | |
| Cobertura (contra o vento) |
-0.710* | -0.888 | 0.80 | 0.8 | 1.0 | 1.0 | -723.13 | |
| -0.315* | -0.394 | 0.80 | 0.8 | 1.0 | 1.0 | -320.99 | ||
| Cobertura (a favor do vento) |
-0.402* | -0.503 | 0.80 | 0.8 | 1.0 | 1.0 | -409.79 | |
| Cobertura (vento cruzado) |
-0.720* -0.400* -0.240* -0.160* |
-0.90 -0.50 -0.30 -0.20 |
0.80 0.80 0.80 0.80 |
0.8 0.8 0.8 0.8 |
1.0 1.0 1.0 1.0 |
1.0 1.0 1.0 1.0 |
-733.23 (0 para h) -407.35 (h a 2h) -244.41 (2h a 3h) -162.94 (> 3h) |
Tabela 13. Calculou as pressões do vento interno atuando simultaneamente com as pressões externas.
* – produto de \({K}_{uma}\) e \({K}_{c,e}\) não deve ser menor que 0.8 (Seção 5.4.3 de AS / NZS 1170.2).
| Superfície | \({V}_{de,θ}\) | \({C}_{FIG,I}\) | \({C}_{p,I}\) | \({K}_{c,I}\) | Pressão de Design \(p ), Nós vamos |
| Pressão interna | 41.20 | 0.0 | 0.0 | 0.8 | 0.0 |
| 41.20 | -0.16 | -0.2 | 0.8 | -162.94 |
Para resumir as pressões do projeto são mostradas na Tabela 14 e 15 combinando o efeito da ação de pressão externa e interna.
Tabela 14. Pressões de vento de projeto calculadas para parede de barlavento.
| altura, m | Pressão externa \({p}_{e}\), Nós vamos | Pressão interna, Nós vamos | Pressão Combinada, Nós vamos | ||
| \({p}_{I,max}\) | \({p}_{I,min}\) | \({p}_{e}-{p}_{I,max}\) | \({p}_{e}-{p}_{I,min}\) | ||
| 3 | 538.64 | 0.00 | -162.94 | 538.64 | 701.58 |
| 6 | 560.16 | 0.00 | -162.94 | 560.16 | 723.10 |
| 9 | 627.25 | 0.00 | -162.94 | 627.25 | 790.19 |
| 10.06 | 570.29 | 0.00 | -162.94 | 570.29 | 733.23 |
Tabela 15. Pressões de vento de projeto calculadas para outras superfícies.
| Superfície | Pressão externa \({p}_{e}\), Nós vamos | Pressão interna, Nós vamos | Pressão Combinada, Nós vamos | ||
| \({p}_{I,max}\) | \({p}_{I,min}\) | \({p}_{e}-{p}_{I,max}\) | \({p}_{e}-{p}_{I,min}\) | ||
| Parede de sotavento | -244.41 | 0.00 | -162.94 | -244.41 | -81.47 |
| Parede lateral (0 a 10,06m) | -529.55 | 0.00 | -162.94 | -529.55 | -366.61 |
| Parede lateral (10.06 a 19,507m) | -407.35 | 0.00 | -162.94 | -407.35 | -244.41 |
| Cobertura (contra o vento) | -723.13 | 0.00 | -162.94 | -723.13 | -560.19 |
| -320.99 | 0.00 | -162.94 | -320.99 | -158.05 | |
| Cobertura (a favor do vento) | -409.79 | 0.00 | -162.94 | -409.79 | -246.85 |
| Cobertura (vento cruzado) | -733.23 (0 para h) -407.35 (h a 2h) -244.41 (2h a 3h) -162.94 (> 3h) |
0.00 | -162.94 | -733.23 (0 para h) -407.35 (h a 2h) -244.41 (2h a 3h) -162.94 (> 3h) |
-570.29 (0 para h) -244.41 (h a 2h) -81.47 (2h a 3h) 0 (> 3h) |
Como o espaçamento de cada quadro é igual a 7,925m, considerando um quadro, as cargas de vento distribuídas equivalentes atuando na estrutura são mostradas nas Figuras 23 e 24. Observe que teremos dois casos de carga a serem considerados, e os valores absolutos máximos da pressão contra o vento do telhado são levados em consideração para cada caso.
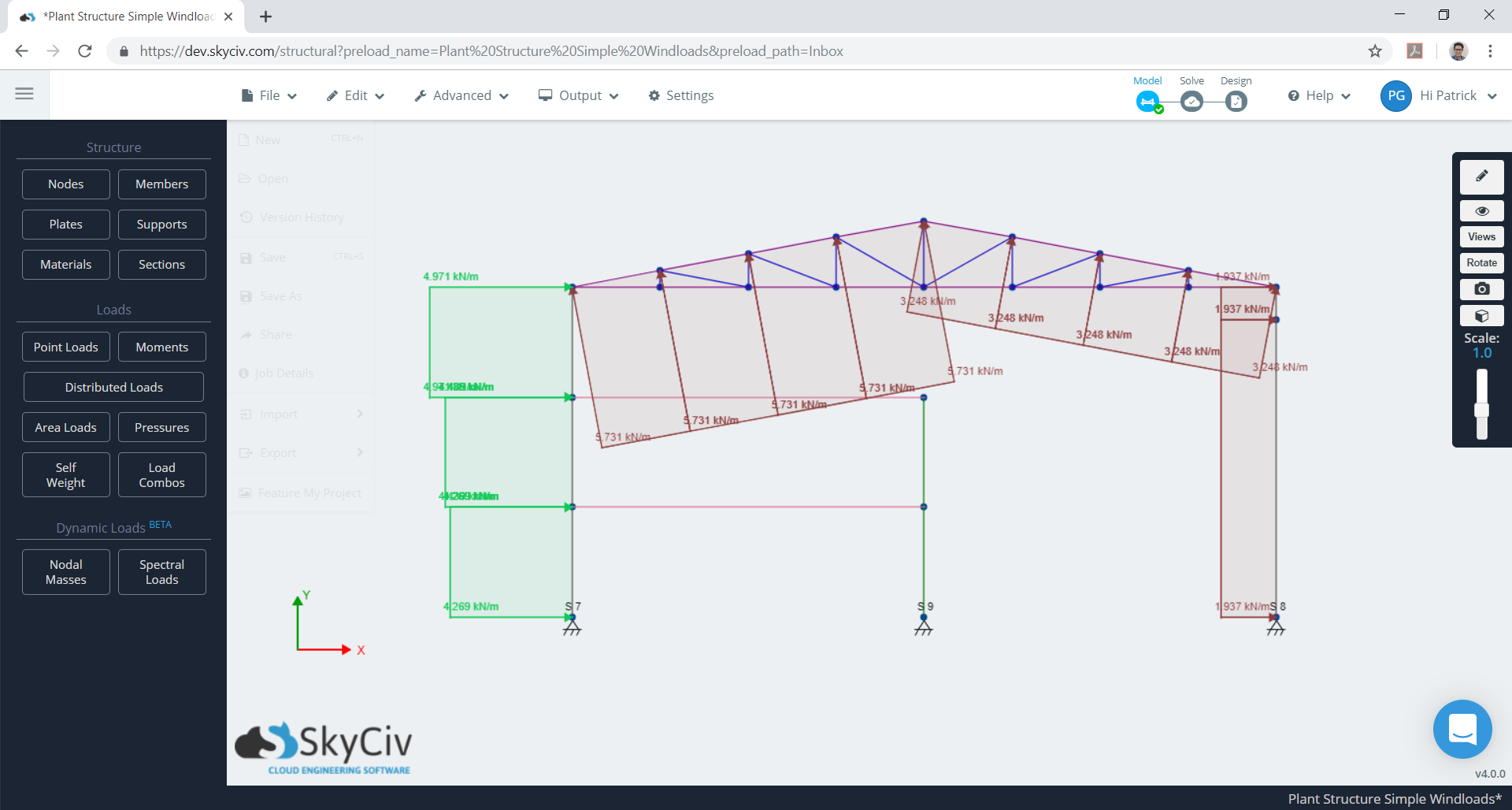
Figura 23. Pressões de vento de design equivalente para um quadro (caso 1).
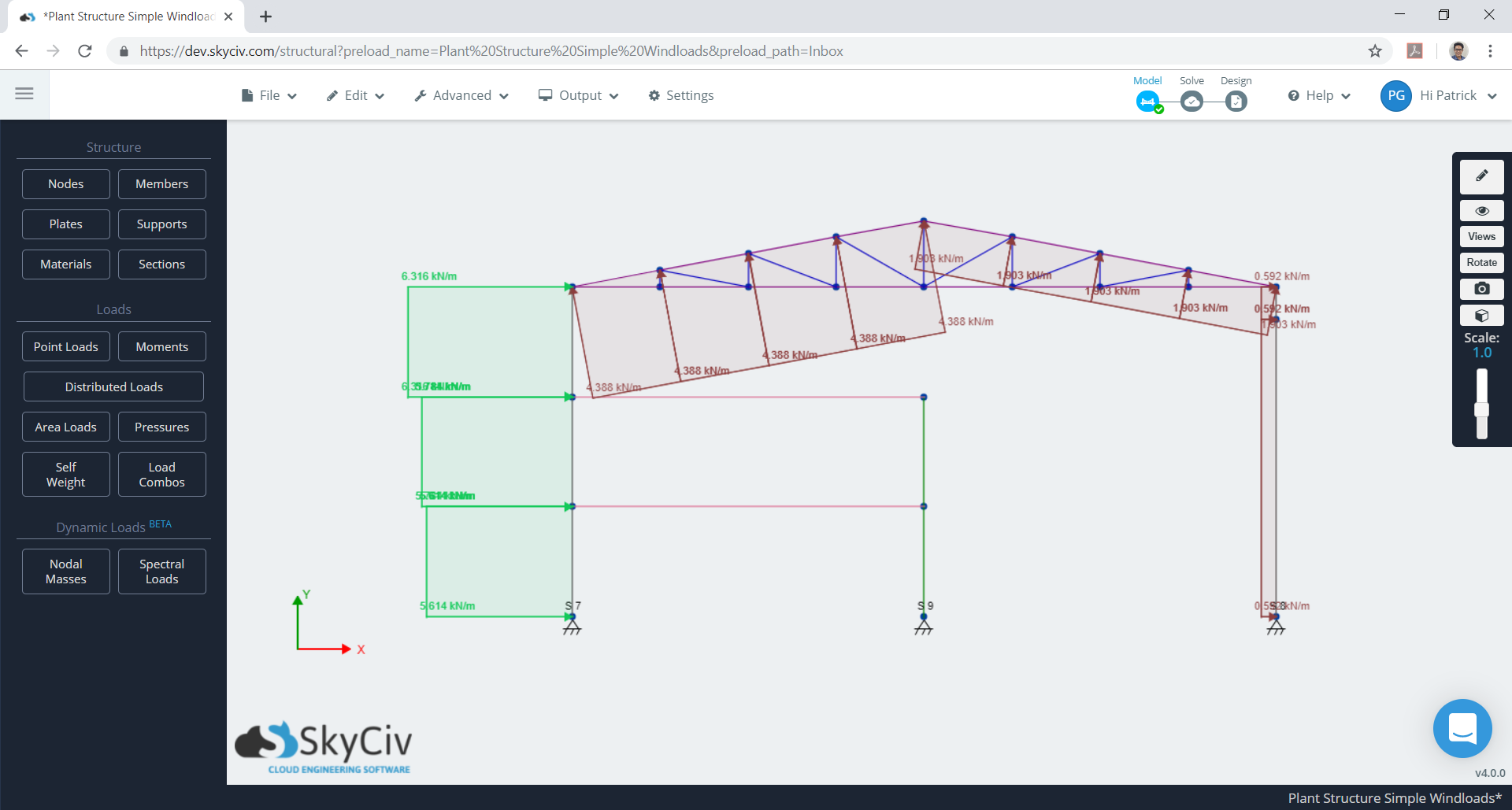
Figura 24. Pressões de vento de design equivalente para um quadro (caso 2).
Todos esses cálculos podem ser realizados usando o Software de carregamento de vento da SkyCiv para ASCE 7-10, 7-16, EN 1991, NBBC 2015, AS 4055 e a norma AS 1170. Os usuários podem inserir a localização do local para obter as velocidades do vento e os fatores topográficos, além de inserir os parâmetros do edifício e gerar as pressões de vento. Com uma conta profissional, os usuários podem aplicar isso automaticamente a um modelo estrutural e executar análises estruturais em um único software.
Caso contrário, tentar nosso SkyCiv Free Wind Toolou reserve um DEMONSTRAÇÃO GRATUITA para obter assistência com seus projetos de engenharia para usuários
Engenheiro estrutural, Desenvolvimento de Produto
MS Engenharia Civil
Referências:
- Comitê Técnico Conjunto. (2011). AS / NZS 1170.2: 2011 Ações de projeto estrutural - Parte 2: Ações do vento. Padrão australiano / neozelandês (AS / NZS), Comitê Técnico Conjunto BD-006, Austrália / Nova Zelândia.



