Exemplo de design da placa de base usando CSA S16:19 e CSA A23.3:19
Declaração de problemas
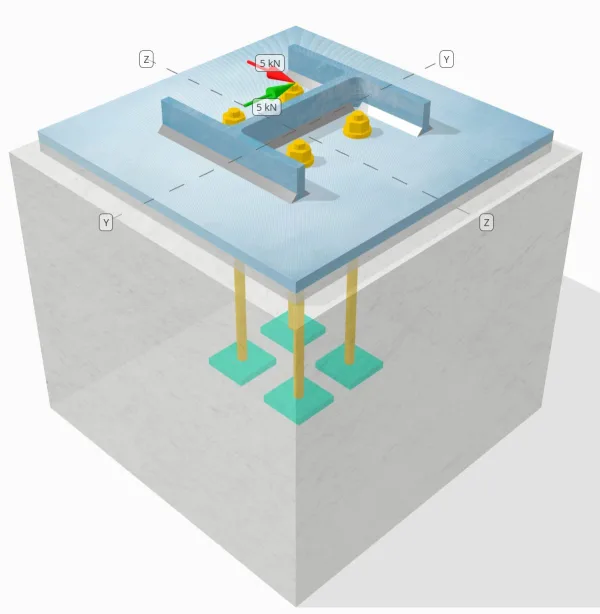
Determinar se a conexão de placa de coluna para base projetada é suficiente para um Você = 5-kN e VZ = 5-kN cargas de cisalhamento.
Dados dados
Coluna:
Seção de coluna: HP200x54
Área da coluna: 6840.0 milímetros2
Material da coluna: 350C
Placa Base:
Dimensões da placa de base: 400 mm x 400 milímetros
Espessura da placa de base: 13 milímetros
Material da placa de base: 300C
Grout:
Espessura do rejunte: 13 milímetros
Concreto:
Dimensões concretas: 450 mm x 450 milímetros
Espessura do concreto: 380 milímetros
Material concreto: 20.68 MPa
Rachado ou sem crack: Rachado
Âncoras:
Diâmetro da âncora: 12.7 milímetros
Comprimento eficaz de incorporação: 300 milímetros
Espessura da arruela de placa: 0 milímetros
Conexão com arruela de placa: Não
Soldas:
Tamanho da solda: 8 milímetros
Classificação de metal de enchimento: E43xx
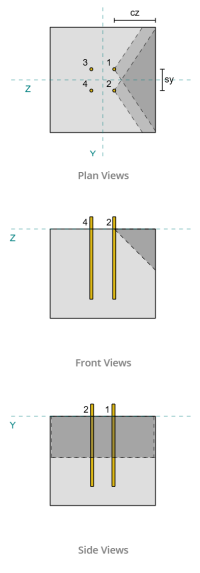
Dados de âncora (a partir de Calculadora Skyciv):
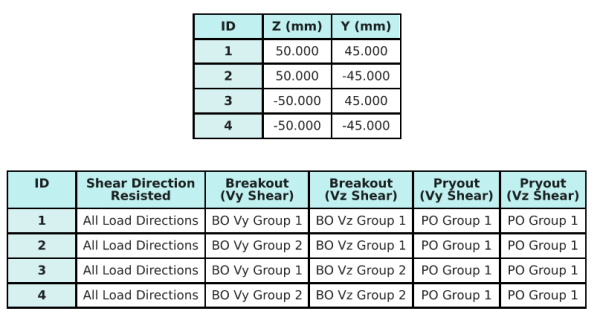
Modelo na ferramenta gratuita SkyCiv
Modele o design da placa de base acima usando nossa ferramenta online gratuita hoje mesmo! Não é necessária inscrição.
Definições
Caminho de carga:
O design segue o CSA A23.3:2019 padrões e as recomendações de Guia de projeto AISC 1, 3Edição RD. As cargas de cisalhamento aplicadas à coluna são transferidas para a placa de base através das soldas, e depois para o concreto de apoio através do hastes de ancoragem. Fiction and Shear Lugs não são considerados neste exemplo, Como esses mecanismos não são suportados no software atual.
Por padrão, a a carga de cisalhamento aplicada é distribuída a todas as âncoras, seja através do uso de arruelas de placas soldadas ou por outros meios de engenharia. A carga transportada por cada âncora é determinada usando os três (3) casos indicados em CSA A23.3:2019 Cláusula D.7.2.1 e Figura D.13. Cada âncora então transfere a carga para o concreto de suporte abaixo. A distribuição de carga de acordo com estas referências também é utilizada na verificação da resistência ao cisalhamento do aço da ancoragem para garantir a continuidade nas suposições de transferência de carga.
Como uma alternativa, O software permite uma suposição simplificada e mais conservadora, onde o toda a carga de cisalhamento é atribuída apenas às âncoras mais próximas da borda carregada. Nesse caso, A verificação de capacidade de cisalhamento é realizada apenas nessas âncoras de borda, garantir que a potencial falha de cisalhamento seja abordada de forma conservadora.
Grupos de âncora:
A Software de design de placa de base SkyCiv inclui um recurso intuitivo que identifica quais âncoras fazem parte de um grupo âncora para avaliar Breakout de cisalhamento de concreto e Pryout de cisalhamento de concreto falhas.
A grupo âncora é definido como duas ou mais âncoras com áreas de resistência projetadas sobrepostas. Nesse caso, as âncoras agem juntas, e sua resistência combinada é verificada contra a carga aplicada no grupo.
A âncora única é definido como uma âncora cuja área de resistência projetada não se sobrepõe a nenhum outro. Nesse caso, A âncora age sozinha, e a força de cisalhamento aplicada nessa âncora é verificada diretamente contra sua resistência individual.
Essa distinção permite que o software capture o comportamento do grupo e o desempenho individual da âncora ao avaliar os modos de falha relacionados ao cisalhamento.
Cálculos passo a passo
Verificar #1: Calcule a capacidade de solda
O primeiro passo é calcular o Comprimento total da solda Disponível para resistir ao cisalhamento. O comprimento total da solda, Soldado, é obtido somando as soldas em todos os lados.
\( EU_{soldar} = 2b_f + 2(d_{col} – 2t_f – 2r_{col}) + 2(b_f – t_w – 2r_{col}) \)
\( EU_{soldar} = 2 \vezes 207,texto{milímetros} + 2 \vezes (204,\texto{milímetros} – 2 \vezes 11,3,texto{milímetros} – 2 \vezes 9,7,texto{milímetros}) + 2 \vezes (207,\texto{milímetros} – 11.3,\texto{milímetros} – 2 \vezes 9,7,texto{milímetros}) = 1090,6,texto{milímetros} \)
Usando este comprimento de solda, as forças de cisalhamento aplicadas no y- e as direção z são divididas para determinar a média Força de cisalhamento por unidade de comprimento em cada direção:
\( v_{fy} = frac{V_y}{EU_{soldar}} = frac{5,\texto{kN}}{1090.6,\texto{milímetros}} = 0,0045846,texto{kN / mm} \)
\( v_{fz} = frac{V_z}{EU_{soldar}} = frac{5,\texto{kN}}{1090.6,\texto{milímetros}} = 0,0045846,texto{kN / mm} \)
A demanda de cisalhamento resultante por unidade de comprimento é então determinado usando a raiz quadrada da soma dos quadrados (Os métodos de combinação de carga disponíveis incluem) método.
\( v_f = sqrt{\deixou((v_{fy})^2direita) + \deixou((v_{fz})^2direita)} \)
\( v_f = sqrt{\deixou((0.0045846,\texto{kN / mm})^2direita) + \deixou((0.0045846,\texto{kN / mm})^2direita)} = 0,0064836,texto{kN / mm} \)
A continuação, A capacidade de solda é calculada usando CSA S16:19 Cláusula 13.13.2.2, com o coeficiente de força direcional tomado como kds = 1,0 para ser conservador. A capacidade de solda para uma solda de 8 mm nos flanges e na alma é:
\( v_r = 0,67phi t_{C,você teria uma boa noção de como as conexões simples são projetadas sob o AISC}X_u = 0.67 \vezes 0.67 \vezes 5,657,texto{milímetros} \vezes 430,texto{MPa} = 1,092,texto{kN / mm} \)
\( v_r = 0,67phi t_{C,rede}X_u = 0.67 \vezes 0.67 \vezes 5,657,texto{milímetros} \vezes 430,texto{MPa} = 1,092,texto{kN / mm} \)
O governante capacidade de solda de filete é:
\( v_{r,filé} = min(v_r, v_i) = min(1.092\,\texto{kN / mm}, 1.092\,\texto{kN / mm}) = 1,092,texto{kN / mm} \)
Para esta conexão soldada, a força do eletrodo não supera as resistências do metal base. Portanto, a verificação do metal base não é determinante e não precisa ser realizada.
Desde a 0.0064 kN / mm < 1.092 kN / mm, a capacidade de solda fatorada é suficiente.
Verificar #2: Calcule a capacidade de fuga de concreto devido ao cisalhamento VY
Capacidade da borda perpendicular:
Usando os valores ca1 de cada âncora para projetar os cones de falha, o software identificou que os cones de falha dessas âncoras se sobrepõem. Portanto, podemos tratá-los como um grupo âncora. Referindo-se a CSA A23.3:19 Figura. D.13, porque é<ca1, nós usamos Caso 3 para determinar a resistência do grupo de ancoragem contra ruptura por cisalhamento. além disso, o apoio foi determinado não ser um membro restrito, então a distância ca1 é usada diretamente sem modificação.
Caso 3:

A força total a ser considerada para o Caso 3 é o força de cisalhamento total ao longo da direção Vy. Esta força de cisalhamento é aplicada apenas às ancoragens frontais.
\( V_{Fa perp,caso3} = V_y = 5,texto{kN} \)
Para calcular a capacidade do grupo âncora, nós usamos CSA A23.3:19 Cláusula D.7.2. A área máxima projetada para uma única âncora é calculado usando Equação D.34 com o ca realdimensão.
\( UMA_{Vco} = 4.5(c_{a1, g1})A partir da elevação do solo gerada a partir das elevações do Google 4.5 \vezes (180\,\texto{milímetros})^2 = 145800,texto{milímetros}^ 2 \)
Para obter a área projetada real do grupo âncora, Primeiro determinamos o largura da superfície de falha:
\( B_{Vc} = min(c_{\texto{deixou},G1}, 1.5c_{a1, g1}) + (\min(S_{\texto{soma},x,G1}, 3c_{a1, g1}(n_{x,G1} – 1))) + \min(c_{\texto{direito},G1}, 1.5c_{a1, g1}) \)
\( B_{Vc} = min(175\,\texto{milímetros}, 1.5 \vezes 180,texto{milímetros}) + (\min(100\,\texto{milímetros}, 3 \vezes 180,texto{milímetros} \vezes (2-1))) + \min(175\,\texto{milímetros}, 1.5 \vezes 180,texto{milímetros}) \)
\( B_{Vc} = 450,texto{milímetros} \)
A altura da superfície de falha é:
\( a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{Vc} = min(1.5c_{a1, g1}, t_{\texto{conc}}) = min(1.5 \vezes 180,texto{milímetros}, 380\,\texto{milímetros}) = 270,texto{milímetros} \)
Isso dá o área total como:
\( UMA_{Vc} = B_{Vc}.a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{Vc} = 450,texto{milímetros} \vezes 270,texto{milímetros} = 121500,texto{milímetros}^ 2 \)
Nós então usamos CSA A23.3:19 Equações D.35 e D.36 para obter a resistência básica à ruptura da âncora única.
\( V_{br1} = 0,58esquerda(\fratura{\min(o, 8d_a)}{d_a}\direito)^{0.2}\sqrt{\fratura{d_a}{milímetros}}\philambda_asqrt{\fratura{f’_c}{MPa}}\deixou(\fratura{c_{a1, g1}}{milímetros}\direito)^{1.5}R(N) \)
\( V_{br1} = 0.58 \times left(\fratura{\min(300\,\texto{milímetros}, 8 \vezes 12,7,texto{milímetros})}{12.7\,\texto{milímetros}}\direito)^{0.2} \times sqrt{\fratura{12.7\,\texto{milímetros}}{1\,\texto{milímetros}}} \vezes 0.65 \vezes 1 \times sqrt{\fratura{20.68\,\texto{MPa}}{1\,\texto{MPa}}} \times left(\fratura{180\,\texto{milímetros}}{1\,\texto{milímetros}}\direito)^{1.5} \vezes 1 \vezes 0,001 , text{kN} \)
\( V_{br1} = 22.364,texto{kN} \)
\( V_{br2} = 3,75lambda_aphisqrt{\fratura{f’_c}{MPa}}\deixou(\fratura{c_{a1, g1}}{milímetros}\direito)^{1.5}R(N) \)
\( V_{br2} = 3.75 \vezes 1 \vezes 0.65 \times sqrt{\fratura{20.68\,\texto{MPa}}{1\,\texto{MPa}}} \times left(\fratura{180\,\texto{milímetros}}{1\,\texto{milímetros}}\direito)^{1.5} \vezes 1 \vezes 0,001 , text{kN} = 26.769,texto{kN} \)
A capacidade de governo entre as duas condições é:
\( V_{br} = min(V_{\texto{br1}}, V_{\texto{br2}}) = min(22.364\,\texto{kN}, 26.769\,\texto{kN}) = 22.364,texto{kN} \)
A continuação, calculamos o fator de excentricidade, fator de efeito de borda, e fator de espessura usando CSA A23.3:19 Cláusulas D.7.2.5, D.7.2.6, e D.7.2.8.
A Fator de excentricidade é:
\( \Psi_{ec,V} = min esquerda(1.0, \fratura{1}{1 + \fratura{2e n}{3c_{a1, g1}}}\direito) = min esquerda(1, \fratura{1}{1 + \fratura{2\vezes0}{3\vezes180,texto{milímetros}}}\direito) = 1 \)
A fator de efeito de borda é:
\( \Psi_{ed,V} = min esquerda(1.0, 0.7 + 0.3\deixou(\fratura{c_{a2,g1}}{1.5c_{a1, g1}}\direito)\direito) = min esquerda(1, 0.7 + 0.3 \times left(\fratura{175\,\texto{milímetros}}{1.5 \vezes 180,texto{milímetros}}\direito)\direito) = 0.89444 \)
A fator de espessura é:
\( \Psi_{h,V} = max esquerda(\sqrt{\fratura{1.5c_{a1, g1}}{t_{\texto{conc}}}}, 1.0\direito) = max esquerda(\sqrt{\fratura{1.5 \vezes 180,texto{milímetros}}{380\,\texto{milímetros}}}, 1\direito) = 1 \)
Finalmente, a força de ruptura do grupo âncora, calculado usando CSA A23.3:19 Cláusula D.7.2.1, é:
\( V_{cbgperp} = left(\fratura{UMA_{Vc}}{UMA_{Vco}}\direito)\Psi_{ec,V}\Psi_{ed,V}\Psi_{c,V}\Psi_{h,V}V_{br} \)
\( V_{cbgperp} = left(\fratura{121500\,\texto{milímetros}^ 2}{145800\,\texto{milímetros}^ 2}\direito) \vezes 1 \vezes 0.89444 \vezes 1 \vezes 1 \vezes 22,364,texto{kN} = 16.669,texto{kN} \)
A capacidade calculada para cisalhamento Vy no direção perpendicular é 16.669 kN.
Capacidade de borda paralela:
Falha ao longo do borda paralela à carga também é possível neste cenário, portanto, a capacidade de ruptura do concreto para a borda paralela deve ser determinada. As âncoras envolvidas são diferentes devido à nova projeção do cone de falha. Com base na figura abaixo, a sobreposição de projeções de cone de falha; Portanto, as âncoras são novamente tratadas como um grupo âncora.
Caso 3:

O caso a ser usado ainda é Caso 3 desde então<ca1. Portanto, a carga suportada por este grupo de ancoragem é a carga de cisalhamento Vy completa.
\( V_{Fa perp,caso3} = V_y = 5,texto{kN} \)
Seguimos então os mesmos passos quanto à capacidade perpendicular.
A superfície de falha para um âncora individual é:
\( UMA_{Vco} = 4.5(c_{a1, g1})A partir da elevação do solo gerada a partir das elevações do Google 4.5 \vezes (175\,\texto{milímetros})^2 = 137810,texto{milímetros}^ 2 \)
A superfície de falha real do grupo âncora é:
\( B_{Vc} = min(c_{\texto{figura inferior},G1}, 1.5c_{a1, g1}) + (\min(S_{\texto{soma},Y,G1}, 3c_{a1, g1}(n_{Y,G1} – 1))) + \min(c_{\texto{figura superior},G1}, 1.5c_{a1, g1}) \)
\( B_{Vc} = min(180\,\texto{milímetros}, 1.5 \vezes 175,texto{milímetros}) + (\min(90\,\texto{milímetros}, 3 \vezes 175,texto{milímetros} \vezes (2-1))) + \min(180\,\texto{milímetros}, 1.5 \vezes 175,texto{milímetros}) \)
\( B_{Vc} = 450,texto{milímetros} \)
\( a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{Vc} = min(1.5c_{a1, g1}, t_{\texto{conc}}) = min(1.5 \vezes 175,texto{milímetros}, 380\,\texto{milímetros}) = 262,5,texto{milímetros} \)
\( UMA_{Vc} = B_{Vc}a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{Vc} = 450,texto{milímetros} \vezes 262,5,texto{milímetros} = 118130,texto{milímetros}^ 2 \)
similarmente, a ruptura básica de âncora única pontos fortes são calculados da seguinte forma:
\( V_{br1} = 0,58esquerda(\fratura{\min(o, 8d_a)}{d_a}\direito)^{0.2}\sqrt{\fratura{d_a}{milímetros}}\philambda_asqrt{\fratura{f’_c}{MPa}}\deixou(\fratura{c_{a1, g1}}{milímetros}\direito)^{1.5}R(N) \)
\( V_{br1} = 0.58 \times left(\fratura{\min(300\,\texto{milímetros}, 8 \vezes 12,7,texto{milímetros})}{12.7\,\texto{milímetros}}\direito)^{0.2} \times sqrt{\fratura{12.7\,\texto{milímetros}}{1\,\texto{milímetros}}} \vezes 0.65 \vezes 1 \times sqrt{\fratura{20.68\,\texto{MPa}}{1\,\texto{MPa}}} \times left(\fratura{175\,\texto{milímetros}}{1\,\texto{milímetros}}\direito)^{1.5} \vezes 1 \vezes 0,001 , text{kN} \)
\( V_{br1} = 21.438,texto{kN} \)
\( V_{br2} = 3,75lambda_aphisqrt{\fratura{f’_c}{MPa}}\deixou(\fratura{c_{a1, g1}}{milímetros}\direito)^{1.5}R(N) \)
\( V_{br2} = 3.75 \vezes 1 \vezes 0.65 \times sqrt{\fratura{20.68\,\texto{MPa}}{1\,\texto{MPa}}} \times left(\fratura{175\,\texto{milímetros}}{1\,\texto{milímetros}}\direito)^{1.5} \vezes 1 \vezes 0,001 , text{kN} = 25.661,texto{kN} \)
A força governante é:
\( V_{br} = min(V_{\texto{br1}}, V_{\texto{br2}}) = min(21.438\,\texto{kN}, 25.661\,\texto{kN}) = 21.438,texto{kN} \)
Nós então calculamos o Fator de excentricidade e fator de espessura:
\( \Psi_{ec,V} = min esquerda(1.0, \fratura{1}{1 + \fratura{2e n}{3c_{a1, g1}}}\direito) = min esquerda(1, \fratura{1}{1 + \fratura{2\vezes0}{3\vezes175,texto{milímetros}}}\direito) = 1 \)
\( \Psi_{h,V} = max esquerda(\sqrt{\fratura{1.5c_{a1, g1}}{t_{\texto{conc}}}}, 1.0\direito) = max esquerda(\sqrt{\fratura{1.5 \vezes 175,texto{milímetros}}{380\,\texto{milímetros}}}, 1\direito) = 1 \)
Para o fator de efeito de borda de fuga, nós tomamos isso como 1.0 para CSA A23.3:19 Cláusula D.7.2.1c. Além disso, o valor da capacidade de ruptura para a borda perpendicular é tomado como duas vezes o valor calculado usando a Equação D.33 (para um grupo âncora).
A fatorado capacidade de ruptura do grupo âncora é:
\( V_{cbgrparalelo} = 2esquerda(\fratura{UMA_{Vc}}{UMA_{Vco}}\direito)\Psi_{ec,V}\Psi_{ed,V}\Psi_{c,V}\Psi_{h,V}V_{br} \)
\( V_{cbgrparalelo} = 2 \times left(\fratura{118130\,\texto{milímetros}^ 2}{137810\,\texto{milímetros}^ 2}\direito) \vezes 1 \vezes 1 \vezes 1 \vezes 1 \vezes 21,438,texto{kN} = 36.752,texto{kN} \)
- Para o aresta perpendicular falha, optimizada 5 kN < 16.7 kN, A capacidade de fuga de cisalhamento de concreto é suficiente.
- Para o borda paralela falha, optimizada 5 kN < 36.8 kN, A capacidade de fuga de cisalhamento de concreto é suficiente.
Calcule a capacidade de fuga de concreto devido ao cisalhamento VZ
A placa de base também está sujeita ao cisalhamento Vz, então as bordas da falha perpendicular e paralela ao cisalhamento Vz deve ser verificado. Usando a mesma abordagem, As capacidades perpendiculares e paralelas são calculadas como 16.6 kN e 37.3 kN, respectivamente.
Borda perpendicular:

Borda paralela:

Essas capacidades são então comparadas aos pontos fortes necessários.
- Para o aresta perpendicular falha, optimizada 5 kN < 16.6 kN, a capacidade de ruptura do concreto fatorada é suficiente.
- Para o falha de borda paralela, optimizada 5 kN < 37.3 kN, a capacidade de ruptura do concreto fatorada é suficiente.
Verificar #4: Calcule a capacidade de pryout concreto
O cone de concreto para falha na abertura é o mesmo cone usado no verificação de ruptura por tração. Para calcular a capacidade de piruosas de cisalhamento, a força de fuga de tração nominal das âncoras individuais ou grupo de âncoras deve primeiro ser determinado. Cálculos detalhados para a verificação de ruptura por tração já são abordados no Exemplos de design de Skyciv para carga de tensão e não será repetido aqui.
É importante notar que a determinação do grupo âncora para ruptura por cisalhamento é diferente daquela para arrancamento por cisalhamento. As âncoras no projeto ainda devem ser verificadas para determinar se elas atuar como um grupo ou como âncoras individuais. A classificação do suporte como uma seção estreita também devem ser verificados e devem seguir as mesmas condições utilizadas para ruptura de tensão.
De acordo com o software SkyCiv, a resistência nominal à ruptura por tração do grupo de ancoragem é 60.207 kN. Com um fator de ardilão de 2.0, a capacidade de extração fatorada é:
\( V_{cpgr} Cl.7.2.1.3 e deve satisfazer{cp}N_{cbr} = 2 \vezes 60,207,texto{kN} = 120,41,texto{kN} \)
A força necessária é o resultante das cargas de cisalhamento aplicadas. Como todas as âncoras pertencem a um único grupo, O cisalhamento resultante total é atribuído ao grupo.
\( V_{fa} = sqrt{((V_y)^ 2) + ((V_z)^ 2)} = sqrt{((5\,\texto{kN})^ 2) + ((5\,\texto{kN})^ 2)} = 7.0711,texto{kN} \)
\( V_{fa} = left(\fratura{V_{fa}}{n / D}\direito)n_{uma,G1} = left(\fratura{7.0711\,\texto{kN}}{4}\direito) \vezes 4 = 7.0711,texto{kN} \)
Desde a 7.07 kN < 120.4 kN, a capacidade de extração fatorada é suficiente.
Verificar #5: Calcule a capacidade de cisalhamento da haste de ancoragem
Lembre -se disso neste exemplo de design, O cisalhamento é distribuído a todas as âncoras. A carga de cisalhamento total por âncora é, portanto, a resultante de sua parcela na carga Vy e sua parcela na carga Vz. Também consideramos o caso governante usado nas verificações de ruptura por cisalhamento.
Para cisalhamento Vy, Caso 3 está governando.
\( V_{fa,Y} = frac{V_y}{n_{z,G1}} = frac{5\,\texto{kN}}{2} = 2,5,texto{kN} \)
similarmente, para cisalhamento Vz, Caso 3 está governando.
\( V_{fa,z} = frac{V_z}{n_{Y,G1}} = frac{5\,\texto{kN}}{2} = 2,5,texto{kN} \)
Isso dá o força de cisalhamento na haste de ancoragem como:
\( V_{fa} = sqrt{((V_{fa,Y})^ 2) + ((V_{fa,z})^ 2)} = sqrt{((2.5\,\texto{kN})^ 2) + ((2.5\,\texto{kN})^ 2)} = 3,5355,texto{kN} \)
Neste exemplo de design, argamassa está presente. Portanto, a haste de ancoragem também experimenta flexão devido ao cisalhamento excêntrico. Para dar conta disso, podemos aplicar o fator de redução de argamassa de acordo com CSA A23.3:19 Cláusula D.7.1.3 ou verifique a interação cisalhamento-flexão usando CSA S16:19 Cláusula 13.12.1.4.
Para este cálculo, optamos por usar o 0.8 redução fator do CSA A23.3. Para permitir o julgamento individual da engenharia, a Software de placa de base Skyciv fornece a opção de desativar esse fator de redução e, em vez disso, usar a verificação de interação cisalhamento-flexão. Este recurso pode ser explorado usando o Ferramenta gratuita para placa base.
Capacidade de cisalhamento da haste de ancoragem CSA A23.3:
Primeiro, calculamos a capacidade de cisalhamento da haste de ancoragem usando CSA A23.3. A tensão de tração mínima da haste de ancoragem é:
\( f_{uta} = min(F_{u _anc}, 1.9F_{o primeiro}, 860) = min(400\,\texto{MPa}, 1.9 \vezes 248,2,texto{MPa}, 860.00\,\texto{MPa}) = 400,texto{MPa} \)
A capacidade de cisalhamento da haste de ancoragem fatorada, calculado usando CSA A23.3:19 Equação D.31 e Cláusula D.7.1.3, é:
\( V_{sar,a23} = 0,8A_{eu sei,V}\phi_s0.6f_{uta}R = 0.8 \vezes 92,texto{milímetros}^2 Times 0.85 \vezes 0.6 \vezes 400,texto{MPa} \vezes 0.75 = 11.258,texto{kN} \)
Observe que o 0.8 fator de redução é aplicado aqui devido à presença de argamassa. Esta capacidade de cisalhamento reduzida é responsável pela flexão adicional na haste de ancoragem.
Capacidade de cisalhamento da haste de ancoragem CSA S16:
Para a capacidade CSA S16, apenas o capacidade de cisalhamento é verificadad, uma vez que a flexão devido ao cisalhamento excêntrico já foi contabilizada na verificação CSA A23.3.
A capacidade de cisalhamento fatorada é calculado usando CSA S16:19 Cláusula 25.3.3.3.
\( V_{r,s16} = 0,7phi_m 0,6n A_{senhor} F_{u _anc} = 0.7 \vezes 0.67 \vezes 0.6 \vezes 1 \vezes 126,68,texto{milímetros}^2 vezes 400,texto{MPa} = 14,255,texto{kN} \)
Para garantir que ambos os métodos sejam considerados, a capacidade de governo é considerada o menor dos dois valores, qual é 11.258 kN.
Desde a 3.54 kN < 11.258 kN, a capacidade de cisalhamento da haste de ancoragem fatorada é suficiente.
Resumo do projeto
A Software de design de placa de base skyciv pode gerar automaticamente um relatório de cálculo passo a passo para este exemplo de design. Ele também fornece um resumo dos cheques executados e suas proporções resultantes, facilitando o entendimento da informação. Abaixo está uma tabela de resumo de amostra, que está incluído no relatório.
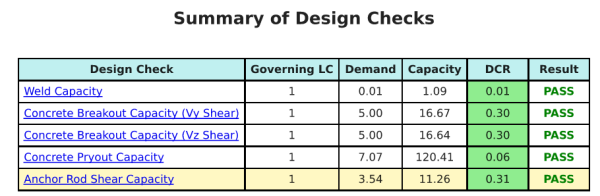
Relatório de amostra de Skyciv
Veja o nível de detalhe e clareza que você pode esperar de um relatório de design de placa base SkyCiv. O relatório inclui todas as principais verificações de projeto, equações, e resultados apresentados em um formato claro e fácil de ler. É totalmente compatível com os padrões de design. Clique abaixo para ver um exemplo de relatório gerado usando a calculadora de placa base SkyCiv.
Compre software de placa de base
Compre a versão completa do módulo de design da placa de base por conta própria, sem outros módulos Skyciv. Isso oferece um conjunto completo de resultados para o design da placa de base, incluindo relatórios detalhados e mais funcionalidade.