Exemplo de design da placa de base usando EN 1993-1-8-2005, EN 1993-1-1-2005 e EN 1992-1-1-2004
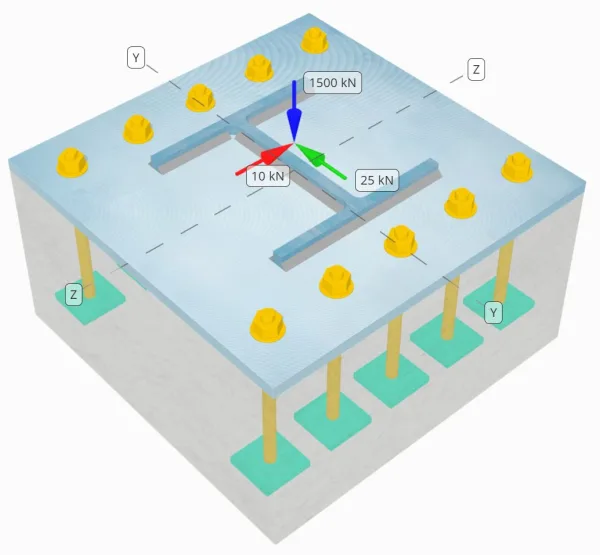
Declaração de problemas
Determine se a conexão projetada da coluna à placa de base é suficiente para uma carga de compressão de 1.500 kN, 12-carga de cisalhamento kN Vz, e carga de cisalhamento Vy de 25 kN.
Dados dados
Coluna:
Seção de coluna: HP 360×180
Área da coluna: 23000 milímetros2
Material da coluna: S275N
Placa Base:
Dimensões da placa de base: 750 mm x 750 milímetros
Espessura da placa de base: 25 milímetros
Material da placa de base: S235
Grout:
Espessura do rejunte: 0 milímetros
Concreto:
Dimensões concretas: 750 mm x 750 milímetros
Espessura do concreto: 380 milímetros
Material concreto: C20/25
Âncoras:
Diâmetro da âncora: 24 milímetros
Comprimento eficaz de incorporação: 300 milímetros
Final de âncora: Placa Retangular
Largura da placa embutida: 100 milímetros
Espessura da placa incorporada: 16 milímetros
Soldas:
Tamanho da solda: 12 milímetros
Classificação de metal de enchimento: E38
Carga de compressão transferida apenas através de soldas? Sim
Dados de âncora (a partir de Calculadora Skyciv):
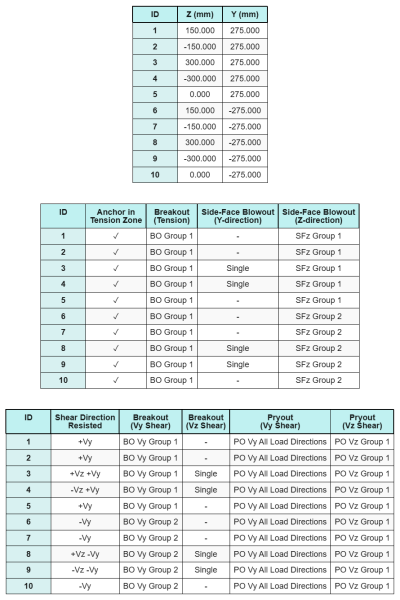
Modelo na ferramenta gratuita SkyCiv
Modele o design da placa de base acima usando nossa ferramenta online gratuita hoje mesmo! Não é necessária inscrição.
Notas
O objetivo deste exemplo de projeto é demonstrar os cálculos passo a passo para verificações de capacidade envolvendo cisalhamento simultâneo e cargas axiais. Algumas das verificações necessárias já foram discutidas nos exemplos de design anteriores. Consulte os links fornecidos em cada seção.
Cálculos passo a passo
Verificar #1: Calcule a capacidade de solda
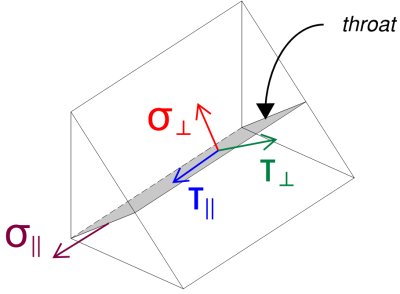
Na determinação da demanda de soldagem, a calculadora SkyCiv assume que o Vy Carga de cisalhamento é resistido pelo web sozinho, a Carga de cisalhamento Vz é resistido pelo flanges sozinhos, quanto pelo carga de compressão é resistido pelo seção inteira.
Primeiro, nós calculamos o Comprimento total da solda na seção.
\(EU_{\texto{soldar}} = 2 b_f + 2(d_{\texto{col}} – 2 t_f – 2 r_{\texto{col}}) + 2(b_f – t_w – 2 r_{\texto{col}})\)
\(EU_{\texto{soldar}} = 2 \vezes 378.8\ \texto{milímetros} + 2 \vezes (362.9\ \texto{milímetros} – 2 \vezes 21.1\ \texto{milímetros} – 2 \vezes 15.2\ \texto{milímetros}) + 2 \vezes (378.8\ \texto{milímetros} – 21.1\ \texto{milímetros} – 2 \vezes 15.2\ \texto{milímetros})\)
\(EU_{\texto{soldar}} = 1992.8\ \texto{milímetros}\)
Então, nós calculamos o comprimentos de solda no flanges quanto pelo rede.
\(EU_{C,flg} = 2 b_f + 2(b_f – t_w – 2 r_{col}) = 2 \vezes 378.8\ \texto{milímetros} + 2 \vezes (378.8\ \texto{milímetros} – 21.1\ \texto{milímetros} – 2 \vezes 15.2\ \texto{milímetros}) = 1412.2\ \texto{milímetros}\)
\(EU_{C,rede} = 2\,(d_{col} – 2t_f – 2r_{col}) = 2 \vezes (362.9\ \texto{milímetros} – 2 \vezes 21.1\ \texto{milímetros} – 2 \vezes 15.2\ \texto{milímetros}) = 580.6\ \texto{milímetros}\)
Considerando os flanges primeiro, a Força de rotação no membro e tensões de cisalhamento são calculados usando EN 1993-1-8:2005 Cláusula 4.5.3.2.
\(\sigma_{\criminoso} = frac{N_x}{EU_{\texto{soldar}} um_{flg} \sqrt{2}} = frac{1500\ \texto{kN}}{1992.8\ \texto{milímetros} \vezes 8.485\ \texto{milímetros} \times sqrt{2}} = 62.728\ \texto{MPa}\)
\(\sua_{\criminoso} = frac{N_x}{EU_{\texto{soldar}} um_{flg} \sqrt{2}} = frac{1500\ \texto{kN}}{1992.8\ \texto{milímetros} \vezes 8.485\ \texto{milímetros} \times sqrt{2}} = 62.728\ \texto{MPa}\)
\(\e_{\paralelo} = frac{V_z}{EU_{C,flg} um_{flg}} = frac{12\ \texto{kN}}{1412.2\ \texto{milímetros} \vezes 8.485\ \texto{milímetros}} = 1.0015\ \texto{MPa}\)
Usando EN 1993-1-8:2005 Eq. (4.1), a tensão de solda de projeto com base no método direcional é então obtido.
\(F_{C,Ed1} = sqrt{(\sigma_{\criminoso})^ 2 + 3\deixou((\sua_{\criminoso})^ 2 + (\e_{\paralelo})^2direita)}\)
\(F_{C,Ed1} = sqrt{(62.728\ \texto{MPa})^ 2 + 3 \times left((62.728\ \texto{MPa})^ 2 + (1.0015\ \texto{MPa})^2direita)}\)
\(F_{C,Ed1} = 125.47\ \texto{MPa}\)
Então, a projeto de tensão perpendicular no metal base é determinado.
\(F_{C,Ed2} = \sigma_{\criminoso} = 62.728\ \texto{MPa}\)
Para a web, usamos a mesma fórmula para calcular o Força de rotação no membro e tensões de cisalhamento, que dá o correspondente tensão de solda de projeto e projeto tensão do metal base.
\(\sigma_{\criminoso} = frac{N_x}{EU_{\texto{soldar}} um_{\texto{rede}} \sqrt{2}} = frac{1500\ \texto{kN}}{1992.8\ \texto{milímetros} \vezes 8.485\ \texto{milímetros} \times sqrt{2}} = 62.728\ \texto{MPa}\)
\(\sua_{\criminoso} = frac{N_x}{EU_{\texto{soldar}} um_{\texto{rede}} \sqrt{2}} = frac{1500\ \texto{kN}}{1992.8\ \texto{milímetros} \vezes 8.485\ \texto{milímetros} \times sqrt{2}} = 62.728\ \texto{MPa}\)
\(\sua_{\paralelo} = frac{V_y}{EU_{C,\texto{rede}} um_{\texto{rede}}} = frac{25\ \texto{kN}}{580.6\ \texto{milímetros} \vezes 8.485\ \texto{milímetros}} = 5.0747\ \texto{MPa}\)
\(F_{C,Ed1} = sqrt{(\sigma_{\criminoso})^ 2 + 3\deixou((\sua_{\criminoso})^ 2 + (\sua_{\paralelo})^2direita)}\)
\(F_{C,Ed1} = sqrt{(62.728\ \texto{MPa})^ 2 + 3 \times left((62.728\ \texto{MPa})^ 2 + (5.0747\ \texto{MPa})^2direita)}\)
\(F_{C,Ed1} = 125.76\ \texto{MPa}\)
\(F_{C,Ed2} = \sigma_{\criminoso} = 62.728\ \texto{MPa}\)
Tomamos então o governando o estresse entre o você teria uma boa noção de como as conexões simples são projetadas sob o AISC e grupos de solda web.
\(F_{C,Ed1} = \max(F_{C,Ed1},\ F_{C,Ed1}) = \max(125.47\ \texto{MPa},\ 125.76\ \texto{MPa}) = 125.76\ \texto{MPa}\)
\(F_{C,Ed2} = \max(F_{C,Ed2},\ F_{C,Ed2}) = \max(62.728\ \texto{MPa},\ 62.728\ \texto{MPa}) = 62.728\ \texto{MPa}\)
A continuação, calculamos a capacidade de soldagem usando EN 1993-1-8:2005 Eq. (4.1). A resistência à tração final (fu) usado nesta equação é o valor mínimo entre a coluna, placa de base, e metal de solda.
\(f_u = \min(f_{você,\texto{col}},\ f_{você,\texto{pb}},\ f_{sua}) = min(370\ \texto{MPa},\ 360\ \texto{MPa},\ 470\ \texto{MPa}) = 360\ \texto{MPa}\)
\(F_{C,RD1} = frac{f_u}{\beta_w\,(\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M2,\text{soldar}})} = frac{360\ \texto{MPa}}{0.8 \vezes (1.25)} = 360\ \texto{MPa}\)
A Resistência do metal base também é calculado usando a mesma equação.
\(F_{C,RD2} = frac{0.9 f_u}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M2,\text{soldar}}} = frac{0.9 \vezes 360\ \texto{MPa}}{1.25} = 259.2\ \texto{MPa}\)
Finalmente, nós comparamos o resistência de solda de filete 🐆 Compre Cialis Sem Prescrição tensão de solda de projeto, quanto pelo resistência de metais básicos 🐆 Compre Cialis Sem Prescrição tensão do metal base.
Desde a 125.76 MPa < 360 MPa, a capacidade de soldagem é suficiente.
Verificar #2: Calcule a capacidade de rolamento de concreto e a capacidade de rendimento da placa de base
Um exemplo de projeto para a capacidade de suporte do concreto e a capacidade de escoamento da placa de base já foi discutido no Exemplo de projeto de placa de base para compressão. Consulte este link para o cálculo passo a passo.
Verificar #3: Calcular a capacidade de suporte da placa de base (Vy cisalhamento)
Quando o cisalhamento é transferido através das hastes de ancoragem, as hastes apoiam-se contra a placa de base. Portanto, precisamos verificar se a placa de base tem capacidade suficiente para resistir ao carga do rolamento nos furos de ancoragem.
A força de cisalhamento de projeto por haste de ancoragem é calculado como o carga de cisalhamento total dividida pelo número total de âncoras.
\(F_{b,Ed} = frac{V_y}{n_{anc}} = frac{25\ \texto{kN}}{10} = 2.5\ \texto{kN}\)
A continuação, determinamos os fatores necessários para o resistência ao rolamento Cálculo. De acordo com EN 1993-1-8:2005 Tabela 3.4, obtemos o \(\alpha_d\), \(\alpha_b\), e \(k_1\) fatores.
Ambos fim e âncoras internas são considerados na determinação do correspondente \(\alpha_d\) fatores.
\(\alfa_{d,\texto{fim}} = frac{eu_{\texto{Beira},Y}}{3 d_{\texto{buraco}}} = frac{100\ \texto{milímetros}}{3 \vezes 26\ \texto{milímetros}} = 1.2821\)
\(\alfa_{d,\texto{interno}} = frac{S_}{3 d_{\texto{buraco}}} – \fratura{1}{4} = frac{550\ \texto{milímetros}}{3 \vezes 26\ \texto{milímetros}} – \fratura{1}{4} = 6.8013\)
Usando o menor \(\alpha_d\) são influenciados principalmente pelas dimensões da sapata, o correspondente \(\alpha_b\) são influenciados principalmente pelas dimensões da sapata é calculado como:
\(\alpha_b = \min\left(\alfa_{d,\texto{fim}},\ \alfa_{d,\texto{interno}},\ \fratura{F_{você,\texto{anc}}}{f_{você,\texto{pb}}},\ 1.0\direito) = min esquerda(1.2821,\ 6.8013,\ \fratura{800\ \texto{MPa}}{360\ \texto{MPa}},\ 1\direito) = 1\)
similarmente, ambos Beira e parafusos internos são considerados na determinação do \(k_1\) fatores.
\(inclui cálculos detalhados passo a passo{1,\texto{Beira}} = min esquerda(2.8\deixou(\fratura{eu_{\texto{Beira},z}}{d_{\texto{buraco}}}\direito) – 1.7,\ 1.4\deixou(\fratura{S_Z}{d_{\texto{buraco}}}\direito) – 1.7,\ 2.5\direito)\)
\(inclui cálculos detalhados passo a passo{1,\texto{Beira}} = min esquerda(2.8 \vezes frac{75\ \texto{milímetros}}{26\ \texto{milímetros}} – 1.7,\ 1.4 \vezes frac{150\ \texto{milímetros}}{26\ \texto{milímetros}} – 1.7,\ 2.5\direito) = 2.5\)
\(inclui cálculos detalhados passo a passo{1,\texto{interno}} = min esquerda(1.4\deixou(\fratura{S_Z}{d_{\texto{buraco}}}\direito) – 1.7,\ 2.5\direito) = min esquerda(1.4 \vezes frac{150\ \texto{milímetros}}{26\ \texto{milímetros}} – 1.7,\ 2.5\direito) = 2.5\)
O governante \(k_1\) são influenciados principalmente pelas dimensões da sapata, correspondente ao menor valor, é:
\(k_1 = \min(inclui cálculos detalhados passo a passo{1,\texto{Beira}},\ inclui cálculos detalhados passo a passo{1,\texto{interno}}) = min(2.5,\ 2.5) = 2.5\)
Finalmente, nós calculamos o resistência ao rolamento usando a equação de EN 1993-1-8:2005 Tabela 3.4.
\(F_{b,Rd} = frac{k_1 \alpha_b f_{u _bp} d_{anc} t_{pb}}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M2, âncora}} \fratura{2.5 \vezes 1 \vezes 360 \texto{ MPa} \vezes 24 \texto{ milímetros} \vezes 25 \texto{ milímetros}}{1.25} = 432 \texto{ kN} \)
Desde a 2.5 kN < 432 kN, a capacidade de suporte da placa de base é suficiente.
Verificar #4: Calcular a capacidade de suporte da placa de base (Vz cisalhamento)
O cálculo para o capacidade de carga sob cisalhamento Vz segue o mesmo procedimento que para Vy cisalhamento, mas considerando a geometria ao longo do Eixo de cisalhamento Vz.
A demanda âncora devido a Vz cisalhamento é:
\(F_{b,Ed} = frac{V_z}{n_{anc}} = frac{12\ \texto{kN}}{10} = 1.2\ \texto{kN}\)
Usando EN 1993-1-8:2005 Tabela 3.4, os fatores são determinados da seguinte forma:
\( \alfa_{d,\texto{fim}} = frac{eu_{\texto{Beira},z}}{3 d_{\texto{buraco}}} = frac{75\ \texto{milímetros}}{3 \vezes 26\ \texto{milímetros}} = 0.96154 \)
\( \alfa_{d,\texto{interno}} = frac{S_Z}{3 d_{\texto{buraco}}} – \fratura{1}{4} = frac{150\ \texto{milímetros}}{3 \vezes 26\ \texto{milímetros}} – \fratura{1}{4} = 1.6731 \)
\( \alpha_b = \min\!\deixou(\alfa_{d,\texto{fim}},\ \alfa_{d,\texto{interno}},\ \fratura{F_{você,\texto{anc}}}{f_{você,\texto{pb}}},\ 1.0\direito) = \min\!\deixou(0.96154,\ 1.6731,\ \fratura{800\ \texto{MPa}}{360\ \texto{MPa}},\ 1\direito) = 0.96154 \)
\(inclui cálculos detalhados passo a passo{1,\texto{Beira}} = \min\!\deixou(2.8\deixou(\fratura{eu_{\texto{Beira},Y}}{d_{\texto{buraco}}}\direito) – 1.7,\ 1.4\deixou(\fratura{S_}{d_{\texto{buraco}}}\direito) – 1.7,\ 2.5\direito)\)
\(inclui cálculos detalhados passo a passo{1,\texto{Beira}} = \min\!\deixou(2.8 \times left(\fratura{100\ \texto{milímetros}}{26\ \texto{milímetros}}\direito) – 1.7,\ 1.4 \times left(\fratura{550\ \texto{milímetros}}{26\ \texto{milímetros}}\direito) – 1.7,\ 2.5\direito) = 2.5\)
\(inclui cálculos detalhados passo a passo{1,\texto{interno}} = \min\!\deixou(1.4\deixou(\fratura{S_}{d_{\texto{buraco}}}\direito) – 1.7,\ 2.5\direito) = \min\!\deixou(1.4 \times left(\fratura{550\ \texto{milímetros}}{26\ \texto{milímetros}}\direito) – 1.7,\ 2.5\direito) = 2.5\)
\(k_1 = \min\!\deixou(inclui cálculos detalhados passo a passo{1,\texto{Beira}},\ inclui cálculos detalhados passo a passo{1,\texto{interno}}\direito) = min(2.5,\ 2.5) = 2.5\)
Finalmente, a projeto de resistência ao rolamento do placa de base é:
\(F_{b,Rd} = frac{k_1 \alpha_b f_{você,pb} d_{anc} t_{pb}}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M2,\text{âncora}}} = frac{2.5 \vezes 0.96154 \vezes 360\ \texto{MPa} \vezes 24\ \texto{milímetros} \vezes 25\ \texto{milímetros}}{1.25} = 415.38\ \texto{kN}\)
Desde a 1.2 kN < 415 kN, a capacidade de suporte da placa de base é suficiente.
Verificar #5: Calcular a capacidade de ruptura do concreto (Vy cisalhamento)
Um exemplo de projeto para a capacidade de ruptura do concreto já foi discutido no Exemplo de projeto de placa base para cisalhamento. Consulte este link para o cálculo passo a passo.
Verificar #6: Calcular a capacidade de ruptura do concreto (Vz cisalhamento)
Um exemplo de projeto para a capacidade de ruptura do concreto já foi discutido no Exemplo de projeto de placa base para cisalhamento. Consulte este link para o cálculo passo a passo.
Verificar #7: Calcule a capacidade de pryout concreto
Um exemplo de projeto para a capacidade do concreto contra a força de cisalhamento já foi discutido no Exemplo de projeto de placa de base para cisalhamento. Consulte este link para o cálculo passo a passo.
Verificar #8: Calcule a capacidade de cisalhamento da haste de ancoragem
Um exemplo de projeto para a capacidade de cisalhamento da haste de ancoragem já foi discutido no Exemplo de projeto de placa de base para cisalhamento. Consulte este link para o cálculo passo a passo.
Resumo do projeto
A Software de design de placa de base skyciv pode gerar automaticamente um relatório de cálculo passo a passo para este exemplo de design. Ele também fornece um resumo dos cheques executados e suas proporções resultantes, facilitando o entendimento da informação. Abaixo está uma tabela de resumo de amostra, que está incluído no relatório.
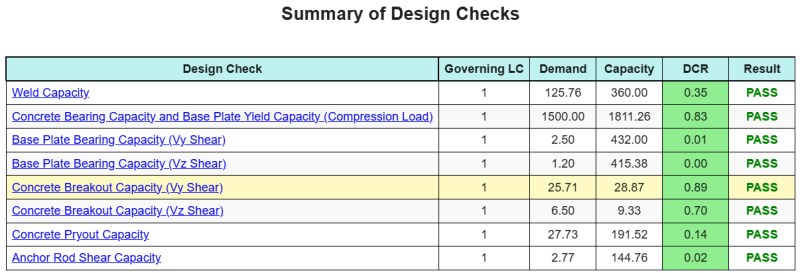
Relatório de amostra de Skyciv
Veja o nível de detalhe e clareza que você pode esperar de um relatório de design de placa base SkyCiv. O relatório inclui todas as principais verificações de projeto, equações, e resultados apresentados em um formato claro e fácil de ler. É totalmente compatível com os padrões de design. Clique abaixo para ver um exemplo de relatório gerado usando a calculadora de placa base SkyCiv.
Compre software de placa de base
Compre a versão completa do módulo de design da placa de base por conta própria, sem outros módulos Skyciv. Isso oferece um conjunto completo de resultados para o design da placa de base, incluindo relatórios detalhados e mais funcionalidade.


