Exemplo de design da placa de base usando EN 1993-1-8-2005, EN 1993-1-1-2005 e EN 1992-1-1-2004
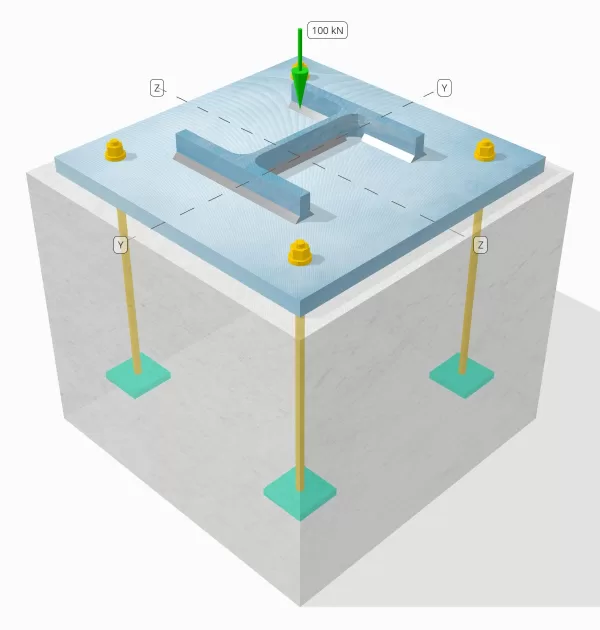
Declaração de problemas
Determine se a conexão de placa coluna para base projetada é suficiente para uma carga de compressão de 100 kN.
Dados dados
Coluna:
Seção de coluna: ELE 200 B
Área da coluna: 7808 milímetros2
Material da coluna: S235
Placa Base:
Dimensões da placa de base: 400 mm x 400 milímetros
Espessura da placa de base: 20 milímetros
Material da placa de base: S235
Grout:
Espessura do rejunte: 20 milímetros
Concreto:
Dimensões concretas: 450 mm x 450 milímetros
Espessura do concreto: 380 milímetros
Material concreto: C20/25
Soldas:
Carga de compressão transferida apenas através de soldas? NÃO
Modelo na ferramenta gratuita SkyCiv
Modele o design da placa de base acima usando nossa ferramenta online gratuita hoje mesmo! Não é necessária inscrição.
Cálculos passo a passo
Verificar #1: Calcule a capacidade de solda
Como a carga de compressão não é transferida sozinha por soldas, É necessária uma superfície adequada do rolamento de contato para garantir que a carga seja transferida por meio de rolamento. Consulte EN 1090-2:2018 Cláusula 6.8 Para preparação de rolamentos de contato.
Além disso, Use o tamanho mínimo da solda Especificado em Eurocódigo.
Verificar #2: Calcule a capacidade de rolamento de concreto e a capacidade de rendimento da placa de base
O primeiro passo é determinar a resistência à compressão do projeto da junta, que depende da geometria do suporte (concreto) e a geometria da área carregada (placa de base).
Começamos calculando o fator alfa, que explica a difusão da força concentrada dentro da fundação.
De acordo com EN 1992-1-1:2004, Cláusula 6.7, O coeficiente alfa é a proporção da área carregada para a área de distribuição máxima, que tem uma forma semelhante à área carregada.
Vamos usar a equação de Papel 6.1 de edifícios de aço de vários andares 5 de Arcelor Mittal, Transportadora peiner, e Corus Para calcular o fator alfa.
\(
\alfa = min esquerda(
1 + \fratura{t_{\texto{conc}}}{\max(EU_{\texto{pb}}, B_{\texto{pb}})},
1 + 2 \deixou( \fratura{Eh}{EU_{\texto{pb}}} \direito),
1 + 2 \deixou( \fratura{e_b}{B_{\texto{pb}}} \direito),
3
\direito)
\)
\(
\alfa = min esquerda(
1 + \fratura{380 \, \texto{milímetros}}{\max(400 \, \texto{milímetros}, 400 \, \texto{milímetros})},
1 + 2 \deixou( \fratura{25 \, \texto{milímetros}}{400 \, \texto{milímetros}} \direito),
1 + 2 \deixou( \fratura{25 \, \texto{milímetros}}{400 \, \texto{milímetros}} \direito),
3
\direito)
\)
\(
\alfa = 1.125
\)
Onde,
\(
e_h = frac{EU_{\texto{conc}} – EU_{\texto{pb}}}{2} = frac{450 \, \texto{milímetros} – 400 \, \texto{milímetros}}{2} = 25 \, \texto{milímetros}
\)
\(
e_b = frac{B_{\texto{conc}} – B_{\texto{pb}}}{2} = frac{450 \, \texto{milímetros} – 400 \, \texto{milímetros}}{2} = 25 \, \texto{milímetros}
\)
Uma vez que a geometria é definida, Em seguida, determinaremos a resistência à compressão do concreto usando EN 1992-1-1:2004, Eq. 3.15.
\(
f_{cd} = frac{\alfa_{inclui cálculos detalhados passo a passo} f_{inclui cálculos detalhados passo a passo}}{\Gamma_c} = frac{1 \vezes 20 \, \texto{MPa}}{1.5} = 13.333 \, \texto{MPa}
\)
A continuação, Assumimos um valor para o coeficiente beta. Já que o rejunte está presente, O valor beta pode ser 2/3. Calcularemos a força do rolamento do projeto da articulação usando as fórmulas combinadas de EN 1993-1-8:2005 Eq. 6.6, e EN 1992-1-1:2004 Eq. 6.63.
\(
f_{inclui cálculos detalhados passo a passo} = beta alpha f_{cd} = 0.66667 \vezes 1.125 \vezes 13.333 \, \texto{MPa} = 10 \, \texto{MPa}
\)
A segunda parte envolve o cálculo da capacidade de rendimento da placa de base.
Já que já temos a força do design da conexão, Usaremos isso para determinar a menor distância do cantilever da placa de base que experimenta a carga completa. Vamos nos referir ao Sci P358 Exemplo na página 243 e EN 1993-1-1:2005 Cláusula 6.2.5.
\(
C = T_{\texto{pb}} \sqrt{\fratura{f_{s_{\texto{pb}}}}{3 f_{inclui cálculos detalhados passo a passo} \a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M0}}} = 20 \, \texto{milímetros} \times sqrt{\fratura{225 \, \texto{MPa}}{3 \vezes 10 \, \texto{MPa} \vezes 1}} = 54.772 \, \texto{milímetros}
\)
Usaremos esta dimensão para calcular a área efetiva da placa de base. O ‘c’ A dimensão que calculamos pode se sobrepor ou não se sobrepor perto do flange. Se se sobrepor, Vamos assumir que a seção é uma seção retangular. Se não se sobrepor, Vamos tomar a forma da coluna.
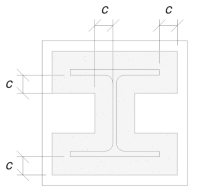
Sem sobreposição
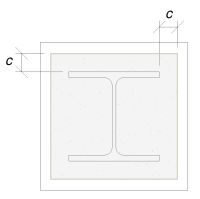
Com sobreposição
Determinamos que o ‘C’ A dimensão não se sobrepõe. Portanto, usando Sci P358 PG. 243, A área efetiva é:
\(
A_e = 4c^2 + a pressão exercida na parede segue uma distribuição vertical uniforme{\texto{col}}c + UMA_{\texto{col}} = 4 \vezes 54.772^2 \, \texto{milímetros}^ 2 + 1182 \, \texto{milímetros} \vezes 54.772 \, \texto{milímetros} + 7808 \, \texto{milímetros}A partir da elevação do solo gerada a partir das elevações do Google 84549 \, \texto{milímetros}^ 2
\)
É importante observar que a área efetiva não deve ser menor que a área da placa de base.
Finalmente, nós vamos usar EN 1993-1-8:2005 Eq. 6.6, e EN 1992-1-1:2004, Eq. 6.63 Para calcular a resistência do rolamento do projeto da conexão da placa de base.
\(
N_{Rd} = left( \min(A_e, A_0) \direito) f_{inclui cálculos detalhados passo a passo} = left( \min(84549 \, \texto{milímetros}^ 2, 160000 \, \texto{milímetros}^ 2) \direito) \vezes 10 \, \texto{MPa} = 845.49 \, \texto{kN}
\)
Desde a 845.49 kN > 100 kN, O design é suficiente!
Resumo do projeto
O software de design da placa de base Skyciv pode gerar automaticamente um relatório de cálculo passo a passo para este exemplo de design. Ele também fornece um resumo dos cheques executados e suas proporções resultantes, facilitando o entendimento da informação. Abaixo está uma tabela de resumo de amostra, que está incluído no relatório.

Relatório de amostra de Skyciv
Veja o nível de detalhe e clareza que você pode esperar de um relatório de design de placa base SkyCiv. O relatório inclui todas as principais verificações de projeto, equações, e resultados apresentados em um formato claro e fácil de ler. É totalmente compatível com os padrões de design. Clique abaixo para ver um exemplo de relatório gerado usando a calculadora de placa base SkyCiv.
Compre software de placa de base
Compre a versão completa do módulo de design da placa de base por conta própria, sem outros módulos Skyciv. Isso oferece um conjunto completo de resultados para o design da placa de base, incluindo relatórios detalhados e mais funcionalidade.


