Berechnung der Axialkräfte eines Fachwerksystems mithilfe der Verbindungsmethode?
In diesem Tutorial, Wir erklären, wie die Verbindungsmethode verwendet wird, um die internen Stabkräfte in einem Fachwerksystem oder einer Fachwerkstruktur zu berechnen.
Diese Kräfte werden als Axialkräfte bezeichnet und sind für die Fachwerkanalyse sehr wichtig. Wenn Sie sich nicht sicher sind, was für ein Fachwerk in unserem Artikel zu sehen ist – Was ist ein Fachwerk?. Die Methode der Verbindungen umfasst im Wesentlichen das Betrachten der einzelnen Gelenke’ (wo sich die Mitglieder treffen) und Anwenden statischer Gleichungen zum Lösen.
Das Tolle ist, SkyCiv Truss erledigt dies automatisch für Sie. Modellieren Sie Ihre eigenen Traversen und die Software zeigt interaktiv Schritt für Schritt, wie Sie die Verbindungsmethode erarbeiten!
Schritt 1: Berechnen Sie die Reaktionen an den Unterstützungen
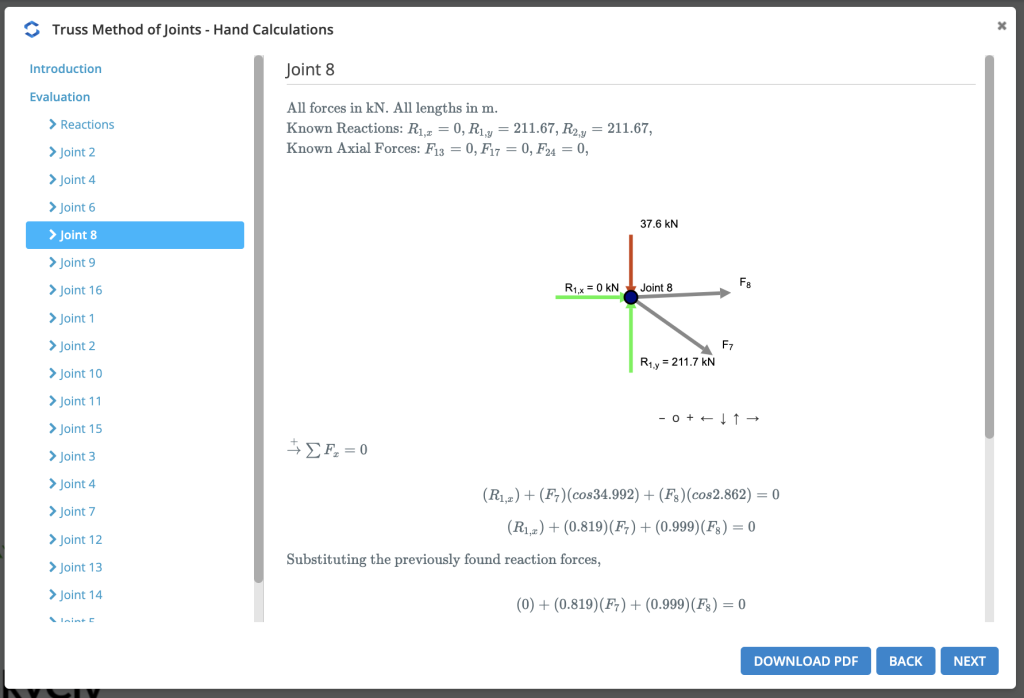
Zuerst, wir berechnen die Reaktionen an den Stützen. Wir beginnen mit einem einfachen Beispiel für a 5 Mitglied Traversensystem:
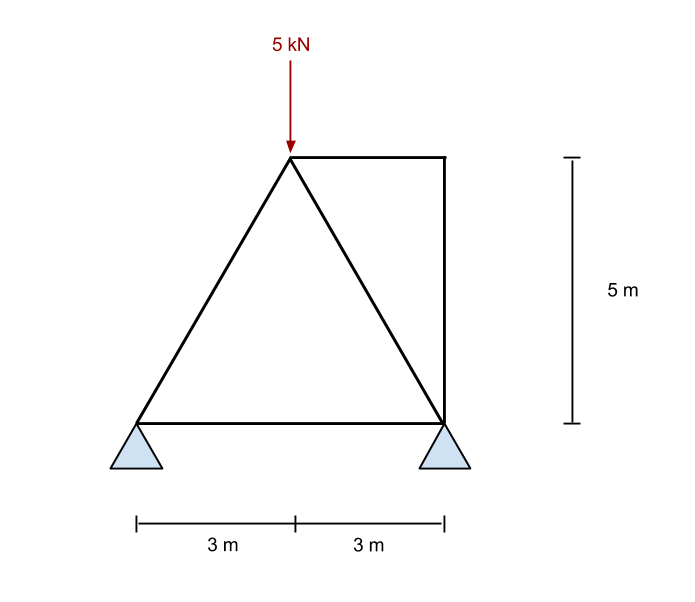
Zur Berechnung der Biegemoment in diesem Traversensystem, Wir nehmen zuerst die Summe der Momente bei der linken Reaktion als Null. Wir tun dies, indem wir alle Mitglieder ignorieren und nur die Kräfte und Stützen in der Struktur betrachten. Dies ist die gleiche Methode wie in den Biegemomentreaktionen in unserem vorherigen Lernprogramm.
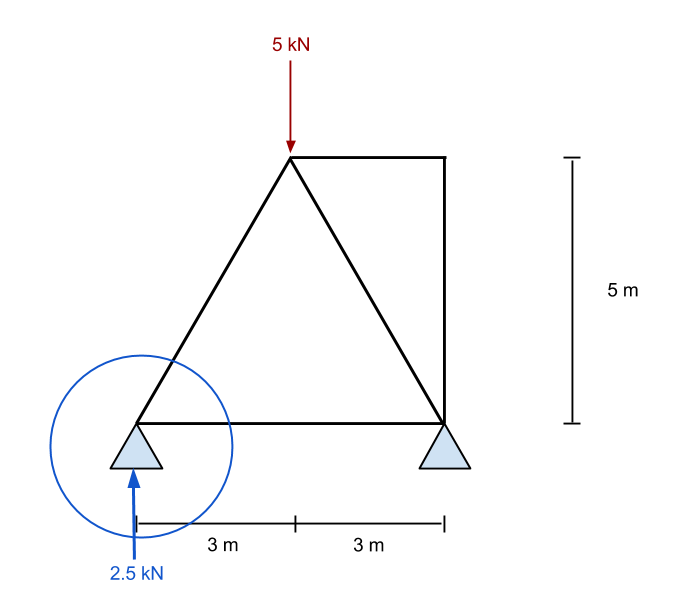
Aus den obigen Gleichungen, Wir lösen nach der Reaktionskraft am Punkt B. (die richtige Unterstützung). In unserem Beispiel, das klappt so 2.5 kN nach oben. Jetzt, wenn wir die Summe der Kräfte im y nehmen (vertikal) Richtung, wir finden diese Unterstützung A. (die linke Unterstützung) wird auch als angegeben 2.5 kN.
Schritt 2: Betrachten Sie eine der Unterstützungen:
Nachdem wir die Reaktionskräfte haben, können wir mit der Analyse des Restes dieser Fachwerkstruktur beginnen. Erstens, Wir schauen auf eine unserer bekannten Kräfte – in diesem Fall, Wir werden die linke Unterstützungsreaktion von betrachten +2.5 kN. Da wir wissen, tritt diese Kraft an diesem Punkt auf, Wir werden genau diesen Punkt isoliert betrachten. Wir wiederholen diesen Vorgang mehrmals, Daher ist es wichtig, den Prozess zu üben und zu lernen, um zu verstehen, wie Axialkräfte in Fachwerkstrukturen gelöst werden können. Also nochmal, Betrachten Sie den ersten Punkt bei der Unterstützung:
In diesen Punkt hineinzoomen, Wir sehen alle bekannten Kräfte, die auf diesen Punkt wirken. Aus der Statik, wir wissen, dass die Kräfte in x- und y-Richtung beide zu Null summieren müssen. Entsprechend, wenn wir wissen, dass es eine vertikale Kraft nach oben gibt, dann muss es eine nach unten gerichtete Kraft geben, um dem entgegenzuwirken. Da haben wir schon den Wert einer nach oben gerichteten Kraft, dann werden wir versuchen, die Mitgliedsnummer zu bewerten 1 zuerst.
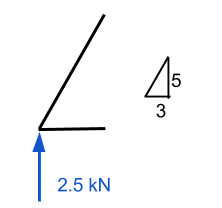
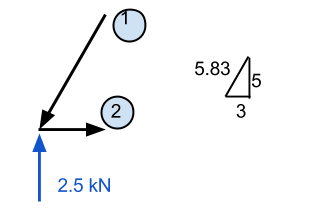
Hier benötigen wir einige Kenntnisse über Vektoren. Es ist wichtig zu bedenken, dass alle Kräfte sowohl für die x- als auch für die y-Richtung zu Null summieren müssen. In unserem Beispiel, Der horizontale Abstand beträgt 3 m, während der vertikale 5 m beträgt – Lassen Sie uns mit der Hypotenuse gleich ungefähr 5.83 Mio.. Verwenden Sie dies, wir können daraus schließen, dass die Normalkraftkomponente des Elements 1 entspricht (5.83)/(5) mal die vertikale Kraft von 2.5 kN. Dies entspricht 2.92 kN und MÜSSEN eine nach unten wirkende Kraft sein, wenn der Punkt stationär bleiben soll.
Mitglied 2 kann auf die gleiche Weise berechnet werden. Wenn wir dieses Mitglied kennen 1 wirkt nach unten, dann wissen wir, dass es auch links handeln muss. Entsprechend, Wir kennen Mitglied 2 muss eine Kraft erzeugen, die den Punkt nach rechts zieht, um die Kräfte in x-Richtung zu halten. Dieser Wert wird berechnet von (3/5.83) x 2.92 kN und ist gleich 1.51 kN.
Schritt 3: Gehen Sie zu einem anderen Punkt:
Nachdem wir die Schnittgrößen des ersten Mitglieds in unserem Fachwerk berechnet haben, Wir werden jetzt auf einen anderen Punkt schauen, um den Vorgang zu wiederholen. Verwendung der Fachwerkbauer kann Ihnen helfen, diese Kräfte automatisch zu visualisieren und Ihre manuellen Berechnungen zu überprüfen.
Nochmal, Wir werden in den Bezugspunkt hineinzoomen und alle bekannten Kräfte betrachten, die auf den Punkt wirken:
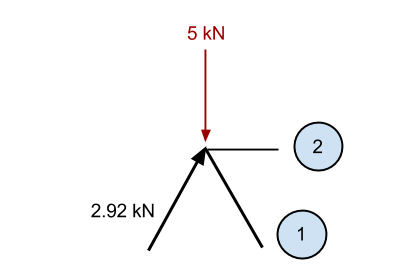
Ähnlich wie zuvor, wenn wir die bekannte vertikale Komponente der 2.92 kN Mitglied (2.5 kN in vertikaler Richtung) und das – 5kN nach unten gerichtete Kraft, dann haben wir Überschuss in Abwärtsrichtung von 2.5 kN (5 – 2.5). Entsprechend, Wir kennen dieses Mitglied 1 muss eine Kraft nach oben verursachen, um den Punkt statisch zu halten. Diese Kraft muss eine vertikale Komponente von haben 2.5 kN, und da es im gleichen Winkel wie das vorherige Mitglied ist, dann muss auch die innere Axialkraft sein 2.92 kN.
Nun betrachten wir die Kräfte in x-Richtung. An dieser Stelle, die gesamte vertikale Kraft vom Element 1 widersteht der Vertikalkraft des zuvor berechneten Elements. Dies bedeutet, dass die Summe der Kräfte in x-Richtung bereits Null ist. Entsprechend, Es kann keine Kraft im Mitglied geben 2 Andernfalls wird der Punkt unausgeglichen und nicht mehr statisch.
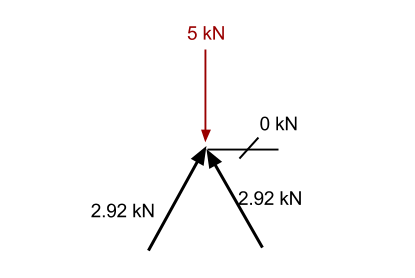
Schritt 4: Gehen Sie zu einem anderen Punkt:
Betrachtet man diesen Punkt, wir können sehen, dass es einen Sonderfall gibt. In dieser Situation, Jede Kraft, die nach oben drückt, kann nicht widerstehen, da es kein anderes Element gibt, das in der Lage ist, eine nach unten gerichtete Kraft bereitzustellen, um den Punkt statisch zu halten. Entsprechend, da die Summe der Kräfte Null sein muss, Diesem Mitglied kann keine Kraft zugeordnet werden. Es, deshalb, hat keine Kraft darin und ist als Null-Mitglied bekannt.
Nochmal, wenn wir die Kräfte in x-Richtung summieren, Wir können sehen, dass es nur ein Element gibt, das eine Kraft in x-Richtung hat. Entsprechend, das muss auch haben 0 Axialkraft, damit die Summe der Kräfte gleich Null ist.

Endgültige Lösung
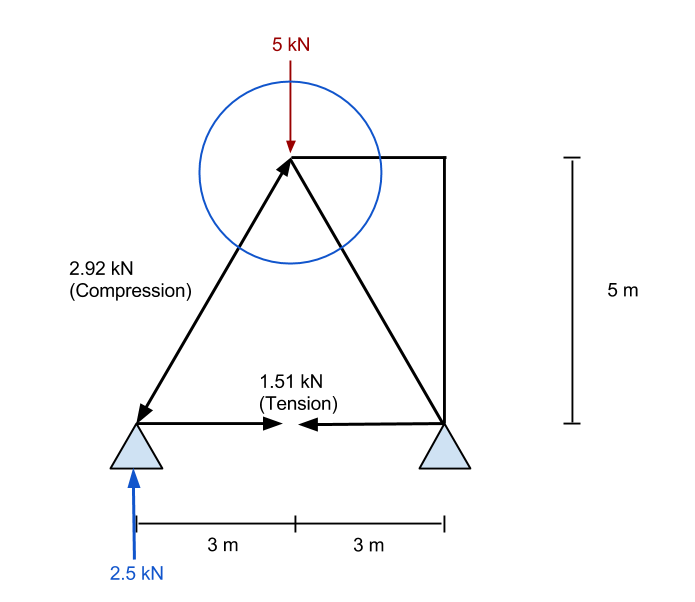
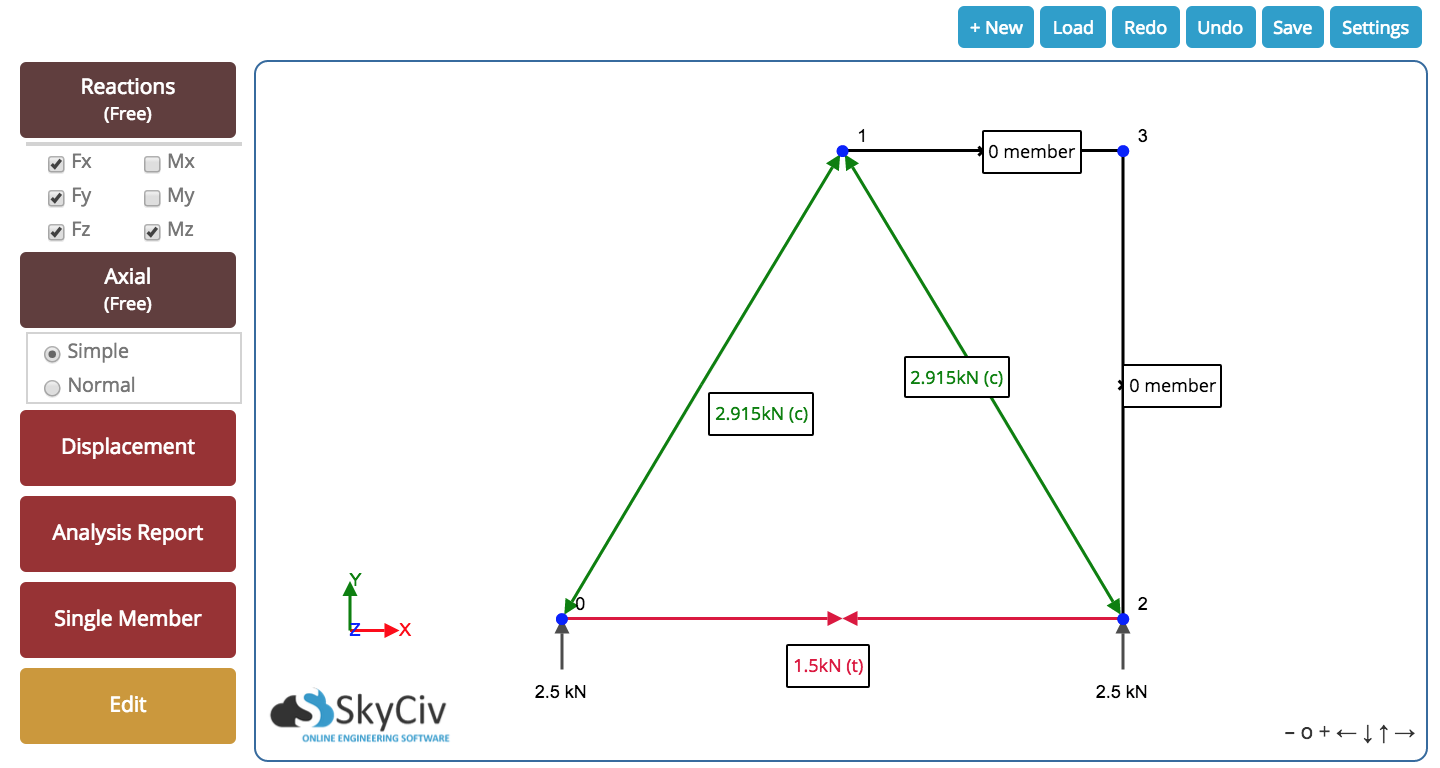
Schließlich, Am Ende erhalten wir das folgende Ergebnis für unser Fachwerk. Wir können alle resultierenden Axialkräfte im Inneren des Stabs sehen und die Reaktionen an den Stützen. Das folgende Ergebnis wurde von unserem genommen Fachwerklöser – probieren Sie es aus, es ist kostenlos!
Einfache Schritte
- Beginnen Sie immer mit der Berechnung der Reaktionen an den Trägern
- Wählen Sie einen Punkt mit bekannter Kraft und betrachten Sie ihn isoliert
- Verwenden Sie die Vektorgeometrie und die Summe der Kräfte = 0 die anderen Mitgliedskräfte zu lösen
- Wiederholen Sie den Vorgang, bis alle Mitglieder gelöst sind
- Denken Sie daran, nach Zero Members Ausschau zu halten
Relevantes Tutorial
- Fachwerk durch Schnittverfahren lösen. Enthält ein Video und eine Schritt-für-Schritt-Anleitung
SkyCiv Truss
SkyCiv Truss kann die Verbindungsmethode automatisch für Sie berechnen. Oder versuchen Sie es mit unserem Kostenloser Rechner für die Konstruktion von Fachwerken die Ihnen die endgültige Antwort geben wird (keine Handberechnungen).
Um weitere Funktionen der SkyCiv-Software zu erkunden, Melden Sie sich noch heute an, um loszulegen!


