Grundlagen des Trägheitsmoments
Das Trägheitsmoment lässt sich als immer ableiten Trägheitsmoment der Teile und Anwendung der Übertragungsformel: ich = ich0 + Anzeige2. Wir haben einen umfassenden Artikel, der den Ansatz erklärt Trägheitsmoment lösen.
Grundsätzlich, das Trägheitsmoment ist das zweite Flächenmoment, was wie folgt ausgedrückt werden kann:
[Mathematik] ICH_{x}=int int y^{2}gibt [Mathematik] [Mathematik] ICH_{j}=int int x^{2}gibt [Mathematik]
Um die Herleitung der folgenden Formeln zu beachten, Wir versuchen, das Trägheitsmoment eines Objekts wie eines Rechtecks um seine Hauptachse einfach mit der obigen Formel zu finden. Um das Trägheitsmoment zu erhalten, die Grenzen sind so zu bestimmen, dass sie von der Drehachse bis zu ihrer äußersten Faser verlaufen. Dies wären die Grenzen des äußeren Integrals. Das innere Integral hat einen Grenzwert von 0 zu b. Das gesagt, wir können dA auch als xdy . ausdrücken, die wird bdy. Da die Drehachse auf der neutralen Achse liegt, das Trägheitsmoment kann mit einer oberen Grenze von h/2 und einer unteren Grenze von integriert werden 0 und wegen der Symmetrie des Rechtecks zweimal multipliziert. Damit bleibt uns das Integral unten.
[Mathematik] ICH_{x}=2int_{0}^{\frac{h}{2}} und ^{2}bdy [Mathematik] Integrieren, [Mathematik] ICH_{x}=2b links [ \frac{und ^{3}}{3} \richtig ]_{0}^{\frac{h}{2}} [Mathematik] [Mathematik] ICH_{x}=2b links [ \frac{h ^{3}}{24}-0 \richtig ] [Mathematik] [Mathematik] ICH_{x}= frac{bh^{3}}{12} [Mathematik]
Trägheitsmomentformel für Balkenabschnitte
SkyCiv hat eine Zusammenfassung der Trägheitsmomentgleichungen für Balkenabschnitte zusammengestellt (zweiter Moment der Fläche). Trägheitsmomentgleichungen sind äußerst nützlich für schnelle und genaue Berechnungen. Die Formeln wurden zu Ihrer Bequemlichkeit in ihre einfachsten Formen zusammengefasst.
SkyCiv bietet auch ein kostenloser Trägheitsmomentrechner für schnelle Berechnungen oder um zu überprüfen, ob Sie die Formel richtig angewendet haben. Die Formel für das Trägheitsmoment für das Rechteck, Kreis, Hohl- und Dreiecksträgerquerschnitte wurden angegeben. Einige wichtige Dinge, die Sie in Bezug auf das Flächenträgheitsmoment eines Balkens beachten sollten, sind::
- Flächenträgheitsmoment unterscheidet sich vom Massenträgheitsmoment
- Es ist auch als das zweite Flächenmoment bekannt
- Es ist ein wesentlicher Faktor der Durchbiegung (je größer das Ix, die untere Auslenkung ist)
- Die Einheiten sind in der Länge hoch 4
- Die folgenden Gleichungen geben das Trägheitsmoment in Bezug auf den Schwerpunkt des Abschnitts
REFERENZ |
Ixx |
Iyy |
Trägheitsmomentgleichung für rechteckige oder rechteckige Querschnitte Section |
||
|---|---|---|
 |
[Mathematik] \dfrac{bh^3}{12} [Mathematik] | [Mathematik] \dfrac{b^{3}h}{12} [Mathematik] |
Trägheitsmomentgleichung für einen hohlen rechteckigen Querschnitt |
||
 |
[Mathematik] \dfrac{bh^3}{12} – \dfrac{b_1h_1^3}{12} [Mathematik] | [Mathematik] \dfrac{b^3h}{12} – \dfrac{b_1^3h_1}{12} [Mathematik] |
Trägheitsmomentgleichung für einen Kreis- oder Kreisquerschnitt |
||
 |
[Mathematik] \dfrac{\Pi}{64}D^4 [Mathematik] | [Mathematik] \dfrac{\Pi}{64}D^4 [Mathematik] |
Trägheitsmomentgleichung für einen hohlen Kreisquerschnitt Cir |
||
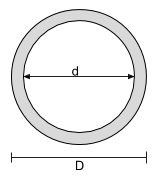 |
[Mathematik] \dfrac{\Pi}{64}D^4 – \dfrac{\Pi}{64}d^4 [Mathematik] | [Mathematik] \dfrac{\Pi}{64}D^4 – \dfrac{\Pi}{64}d^4 [Mathematik] |
Trägheitsmomentgleichung für ein gleichschenkliges Dreieck |
||
 |
[Mathematik] \dfrac{bh^3}{36} [Mathematik] | [Mathematik] \dfrac{3b^3h}{144} [Mathematik] |
Trägheitsmomentgleichung eines I-Profils |
||
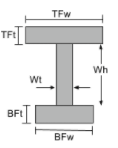 |
[Mathematik] \frac{TFwtimes TFt^{3}}{12} +\frac{Wttimes Wh^{3}}{12} + \frac{BFwtimes BFt^{3}}{12} +[Mathematik] [Mathematik] TFw times TFt times left ( BFt + Wh +frac{TFt}{2} -\Bar{j}_{bot} \richtig )^{2} +[Mathematik] [Mathematik] Wt times Wh times left ( BFT + frac{Wh}{2} -\Bar{j}_{bot} \richtig )^{2} +[Mathematik] [Mathematik] BFw times BFt times left ( \frac{Wh}{2} -\Bar{j}_{bot} \richtig )^{2} [Mathematik] | [Mathematik] \frac{TFttimes TFw^{3}}{12} + \frac{Whtimes Wt^{3}}{12} + \frac{BFttimes BFw^{3}}{12} [Mathematik] |
Trägheitsgleichung eines T-Profils- |
||
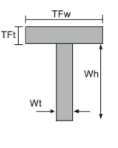 |
[Mathematik] \frac{TFwtimes TFt ^{3}}{12} + \frac{Wttimes Wh ^{3}}{12} +[Mathematik] [Mathematik] TFwtimes TFtlinks ( Wh + \frac{TFt}{2} -\Bar{j}_{bot} \richtig )^{2} +[Mathematik] [Mathematik] Wttimes Wh times left ( \frac{Wh}{2} – \Bar{j}_{bot} \richtig )^{2} [Mathematik] | [Mathematik] \frac{TFttimes TFw ^{3}}{12} + \frac{Whtimes Wt ^{3}}{12} [Mathematik] |
Trägheitsmoment-Gleichung eines Kanalabschnitts |
||
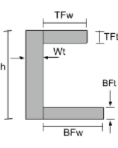 |
[Mathematik] \frac{TFwtimes TFt^{3}}{12} + \frac{BFwtimes BFt^{3}}{12} + \frac{Wt times h^{3}}{12} +[Mathematik] [Mathematik] TFw times TFt times left ( h – \frac{TFt}{2} – \Bar{j}_{bot} \richtig )^{2} +[Mathematik] [Mathematik] BFw times BFt times left ( \frac{BFt}{2} – \Bar{j}_{bot} \richtig )^{2} +[Mathematik] [Mathematik] Wt times h times left ( \frac{h}{2} – \Bar{j}_{bot} \richtig )^{2} [Mathematik] | [Mathematik] \frac{TFttimes TFw^{3}}{12} + \frac{BFttimes BFw^{3}}{12} + \frac{h times Wt^{3}}{12} +[Mathematik] [Mathematik] TFt times TFw times left ( Wt + \frac{TFw}{2} – \Bar{x}_{links} \richtig )^{2} +[Mathematik] [Mathematik] BFt times BFw times left ( Wt + \frac{BFw}{2} – \Bar{x}_{links} \richtig )^{2} +[Mathematik] [Mathematik] h times Wt times left ( \frac{Wt}{2} – \Bar{x}_{links} \richtig )^{2} [Mathematik] |
Trägheitsmoment Gleichung der Winkel |
||
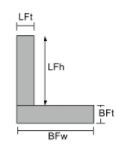 |
[Mathematik] \frac{BFwtimes BFt^{3}}{12} + \frac{ LFt times LFh^{3}}{12} +[Mathematik] [Mathematik] BFw times BFt times left ( \frac{BFt}{2}-\Bar{j}_{bot} \richtig )^{2} +[Mathematik] [Mathematik] LFt times LFhtimes left ( BFt + \frac{LFh}{2}-\Bar{j}_{bot} \richtig )^{2} [Mathematik] | [Mathematik] \frac{BFttimes BFw^{3}}{12} + \frac{ LFh times LFt^{3}}{12} +[Mathematik] [Mathematik] BFt times BFw times left ( \frac{BFw}{2}-\Bar{x}_{links} \richtig )^{2} +[Mathematik] [Mathematik] LFh times LFttimes left ( \frac{LFt}{2}-\Bar{x}_{links} \richtig )^{2} [Mathematik] |
Verwenden Sie SkyCiv Section Builder für Handberechnungen
In diesem Artikel, Wir haben Sie durch die Formel des Trägheitsmoments geführt. Weitere Informationen zu diesem Thema, Besuchen Sie unser Tutorial auf Trägheitsmoment des Balkenabschnitts.
Wusstest du schon SkyCiv Section Builder zeigt auch die vollständigen Berechnungen für die folgenden Formen?
- Rechteckig, Hohl rechteckig
- Kreisförmig, Hohlkreis
- Ich glänze, T-Beam
- Winkel (L-Beam), Kanal
- Dreieckige Abschnitte
Wir hoffen, dass Sie die obige Tabelle nützlich finden, um das Trägheitsmoment eines Kreises zu berechnen, Dreieck, und rechteckiges Trägheitsmoment unter anderen Formen. Wir haben auch ein nützliches Trägheitsmomentrechner, eine vereinfachte von SkyCiv Section Builder, das diese Berechnungen für Sie durchführt, oder melden Sie sich noch heute an, um mit der SkyCiv-Software zu beginnen!


