Descrição geral
SkyCiv possui módulo robusto e avançado para projeto de lajes de concreto armado. Para acessar este recurso, você deve primeiro ter construído um modelo no SkyCiv S3D e depois chamar o módulo para cálculo automático com diferentes códigos de construção, como ACI-318, Padrões europeus e australianos, e assim por diante. O objetivo principal do módulo para o projeto da placa é fornecer a quantidade de vergalhões de reforço de aço ao longo da placa..
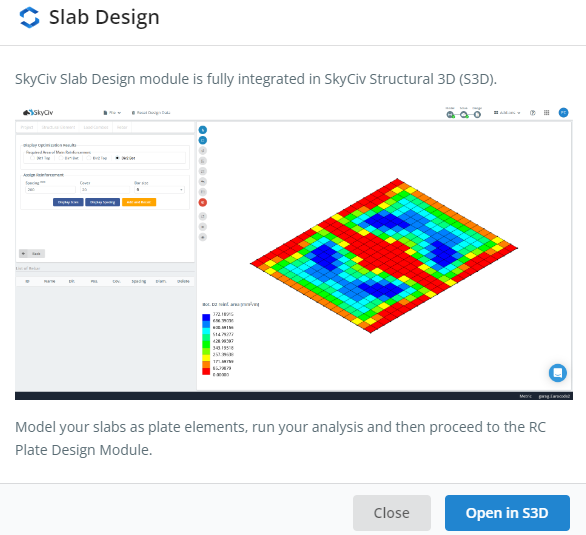
Figura 1. Módulo de design de laje SkyCiv
Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!
A documentação SkyCiv fornece conteúdo excelente, incluindo exemplos e casos de análise, tanto para aprender, se você for novo nos módulos, quanto para comparar os resultados do módulo de design de placas com cálculos manuais. Sinta-se à vontade para verificar nossos exemplos de design de acordo com ACI-318, Eurocódigo, e AS3600.
Sugerimos que você leia este artigo antes de analisar profundamente sistemas complexos de lajes. Aqui, você aprenderá como os momentos fletores diferem dependendo das dimensões da planta da laje. Existem dois casos de estudo, lajes unidirecionais e bidirecionais. Então, vamos começar a ler!
Comportamento de laje unidirecional versus bidirecional
Vamos considerar o exemplo da laje na imagem a seguir, onde há apoio em cada borda da laje, e estabelecemos que isso se comportará como uma placa bidirecional, enquanto a tensão no aço fs é menor que a tensão de escoamento f, tendo um momento fletor nas duas direções principais do plano.
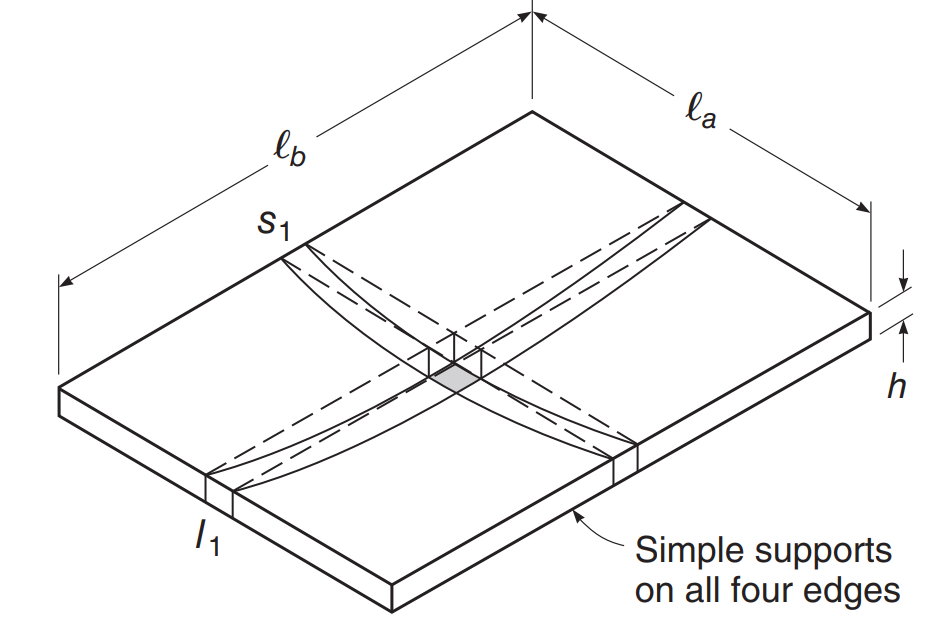
Figura 2. Exemplo simples de laje bidirecional na flexão. (David Darwin, Charles W.Dolan, Artur H.. Nilson, “são influenciados principalmente pelas dimensões da sapata,” Décima Quinta Edição, Educação McGraw-Hill)
Podemos definir o deslocamento vertical como (\(eu_a < Libra \)):
\(\Delta_a = frac{{5}{e_a}{eu_a^4}}{384{E}{I}}\)
\(\Delta_b = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
Devido à laje ser um sistema contínuo, ambas as deflexões verticais terão o mesmo valor. Podemos comparar as equações para expressar uma relação entre a carga transportada por cada direção em função das dimensões do plano.
\(\Delta_a = Delta_b para frac{{5}{e_a}{eu_a^4}}{384{E}{I}} = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
\(\fratura{e_a}{w_b} = {(\fratura{Libra}{eu_a}})^4 \)
Todas as referências de concreto armado para projeto de lajes se dividem em unidirecionais e bidirecionais se o quociente de \(\fratura{Libra}{eu_a}\) é maior ou menor que um valor de 2, respectivamente.
Usando as equações acima, quando \(\fratura{Libra}{eu_a}=2), a carga transportada pela direção curta é igual a \(w_a = {16}{w_b}\) e quando o valor for \(\fratura{Libra}{eu_a}=1), a carga é distribuída igualmente em ambas as direções \(w_a ={w_b}\).
Momentos de lajes unidirecionais
Então, podemos ver que quando o quociente de dimensões é maior que 2, praticamente, todas as cargas e momentos fletores estarão concentrados apenas na direção curta. Este caso é o comportamento da laje unidirecional, e o momento fletor máximo pode ser obtido como uma viga simplesmente apoiada com largura unitária.
\(M_{max,1,D}= frac{{e_a}{1 m}{eu_a^2}}{8}\)
Momentos de lajes bidirecionais
A solução do caso da laje dupla é um problema complexo e desafiador em mecânica estrutural. Você pode ver na figura abaixo que a análise geral consiste em uma placa com forças e momentos inteiros em cada direção.
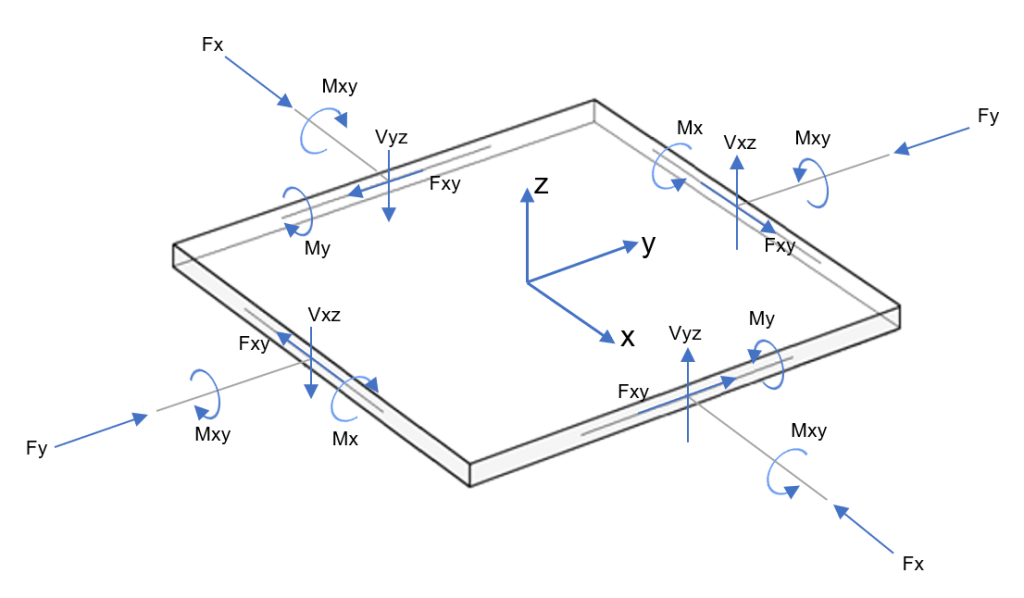
Figura 3. Ações no elemento de placa (momentos fletores e torcionais; forças normais e de cisalhamento)
Esta dificuldade vem do problema real a ser resolvido é uma equação diferencial parcial de quarta ordem que envolve a flexão em duas direções. A forma desta equação é:
\(\fratura{\parcial^4{C}}{{\parcial}{x^4}} + {2}\fratura{{\parcial^4}{C}}{{{\parcial}{x^2}}{{\parcial}{y ^ 2}}}+\fratura{\parcial^4{C}}{{\parcial}{x^4}}-\fratura{f_z}{D} = 0\)
Onde a rigidez da placa (usando as propriedades mecânicas e geométricas elásticas) é \(D=frac{{E}{t^3}}{{12}{(1-\não ^ 2)}}\).
A solução analítica desta equação só está disponível para condições de apoio simples. A única maneira de obter uma solução possível para casos reais e práticos é através de métodos numéricos como o Método dos Elementos Finitos.
SkyCiv usa esta abordagem para resolver análise de placas. Nos links a seguir, você terá acesso a tutoriais para conhecer as características da plataforma SkyCiv: Projeto de placas em S3D e Como modelar placas? .
Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!


