Como calcular uma viga indeterminada – Método da Integral Dupla

Indeterminado feixes pode ser um desafio por causa das etapas extras necessárias para resolver as reações. Lembre-se de que as estruturas indeterminadas têm o que é chamado de grau de indeterminação. Para resolver a estrutura, condições de contorno devem ser introduzidas. Consequentemente, quanto maior o grau de indeterminação, mais condições de contorno devem ser identificadas. Mas antes que possamos resolver um feixe indeterminado, primeiro precisamos identificar se o feixe é estaticamente indeterminado. Como as vigas são estruturas unidimensionais, usar a equação para determinar estruturas externamente estaticamente indeterminadas é suficiente.

[math]
eu_{e}=R-esquerda ( 3+e_{c} \direito )
[math]

Onde:

• I_e = Grau de indeterminação
• R = Número total de reações
• e_c = Condições externas (por exemplo. dobradiça interna)

Normalmente, no entanto, sem a necessidade de resolver o grau de indeterminação, qualquer coisa que não sejam vãos simples ou vigas em balanço são estaticamente indeterminadas, assumindo que tais vigas não vêm com dobradiças internas.

Existem muitas maneiras de abordá-lo para resolver vigas indeterminadas. Embora por uma questão de simplicidade e semelhança com o SkyCiv Beam os cálculos manuais, discutiremos o método de Integração Dupla.

Integração Dupla

A Integração Dupla é talvez o mais simples de todos os métodos para a análise de vigas. O conceito deste método é bastante direto ao contrário de outros métodos, pois se baseia principalmente em uma compreensão básica do cálculo integral, daí o nome. Um pouco de cálculo integral é adaptado da relação da curvatura da viga com o momento mostrado abaixo.

[math]
\fratura{1}{\rho}= frac{M}{NÃO}
[math]

Observe que 1/ρ é a curvatura da viga e que ρ é o raio da curva. Fundamentalmente, a definição de curvatura é a taxa de variação da tangente em relação ao comprimento do arco. Como o momento é uma função do carregamento em relação ao comprimento da barra, integrando a curvatura em relação ao comprimento do membro produzirá a inclinação da viga. similarmente, integrar a inclinação em relação ao comprimento do membro produzirá a deflexão da viga. Como as cargas estruturais típicas são de natureza algébrica, a integração dessas expressões é tão simples quanto usar a fórmula geral de potência.

[math]
\int fesquerda ( xdireita )^{n}dx=frac{fesquerda ( xdireita )^{n+1}}{n+1}+C
[math]

Talvez a melhor maneira de entender o conceito seja fornecer um exemplo de uma viga com o seguinte dado.

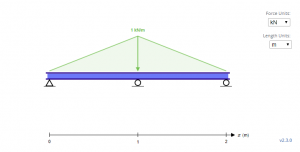
A viga de amostra acima é uma viga indeterminada com carregamentos triangulares. Com o tipos de apoios, A_Y, B_Y e C_Y pela primeira vez, segundo, e terceiros suportes respectivamente, o primeiro passo para resolver essas incógnitas é começar com as equações de equilíbrio.

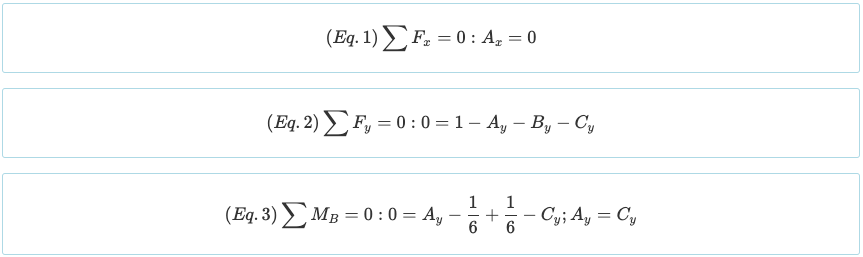
Note que a viga tem um grau de indeterminação estática de 1°. Como existem quatro incógnitas (A_x, A_Y, B_Y, e C_Y) e há três equações tão distantes das equações de equilíbrio acima, é necessário criar mais uma equação a partir das condições de contorno. Lembre-se de que o momento gerado por uma carga pontual e uma carga triangular são os seguintes.

Carga Pontual:

[math]
M=Fvezes x; M = F x
[math]

Carga triangular:

[math]
M=frac{c_{0}\vezes x}{2}\times left ( \fratura{x}{3} \direito ); M = frac{c_{0}x^{2}}{6}
[math]

Usando o método de dupla integração, essas novas equações são feitas e exibidas abaixo.

Observação: As equações acima são escritas como funções de Macaulay onde uma expressão é igual a zero quando x < L. Nesse caso, L = 1.

Nas equações acima, observe que o quarto termo adicionado parece surgir do nada. Na verdade, a direção do carregamento é oposta à direção da gravidade. Isso se deve ao fato de que as equações para cargas triangulares só funcionam quando a carga é ascendente à medida que o comprimento aumenta. Isso não é um grande problema para equações para distribuído e cargas pontuais devido a sua simetria. Em vigor, a carga equivalente para a viga acima se parece com a viga abaixo, assim as equações são baseadas nele.

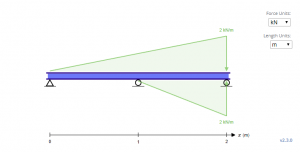
Para resolver para C₁ e C₂, as condições de contorno devem ser determinadas. No feixe acima, pode-se observar que existem três dessas condições de contorno em x = 0, x = 1, e x = 2, onde a deflexão y é zero nos três locais.

Condição de contorno 1

[math]
x=0, y=0; C_{2}= 0
[math]

Condição de contorno 2

[math]
x=0, y=0; C_{1}= frac{1}{120}-\fratura{UMA_{Y}}{6}
[math]

Depois de determinar os valores de cada constante, a última equação agora pode ser obtida usando a última condição de contorno.

Condição de contorno 3

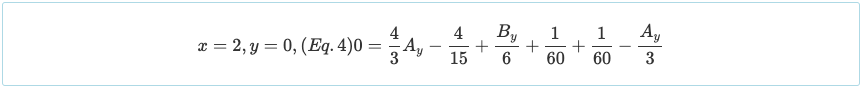
Observe que a condição de contorno de θ = 0 em x = 1 pode ser usado, embora seja aplicável apenas para a reação intermediária de uma viga contínua simétrica com carregamento simétrico.

Como as quatro equações foram determinadas, eles agora podem ser resolvidos simultaneamente. A resolução dessas equações produzirá as seguintes reações.

Com as reações determinadas, os valores das reações podem ser substituídos de volta à equação do momento. Isso nos permitirá determinar o valor do momento em qualquer parte do sistema de vigas.

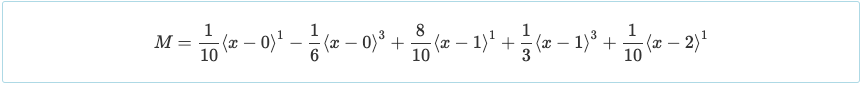
Outra conveniência da Integração Dupla é que a equação do momento é apresentada de uma forma que pode ser usada para resolver o cisalhamento com a relação mostrada abaixo.

[math]
V=frac{dM}{dx}
[math]

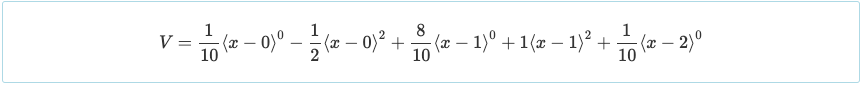
Novamente, usando apenas uma compreensão básica do cálculo diferencial, igualar a derivada de uma função a zero produz o máximo ou mínimo dessa função. Por isso, igualando V = 0 resultará em um momento positivo máximo em x = 0.447 e x = 1.553 de M = 0.030

É claro, tudo isso pode ser verificado com SkyCiv Beam.

Software SkyCiv Beam

O software de análise de vigas SkyCiv permite que os usuários analisem vigas com facilidade e precisão. Você pode obter uma análise das suas vigas, incluindo reações, forças de corte, momentos de flexão, deflexões, e esforços em questão de segundos.

Se você quiser experimentar primeiro, a Calculadora de vigas grátis é uma ótima maneira de começar, ou simplesmente inscreva-se gratuitamente hoje!