Índice
- Tipos de suportes e suas reações
- Uma guia passo a passo sobre como determinar as reações de suporte em vigas
- Software SkyCiv Beam
Tipos de suportes e suas reações
Primeiro, é importante também conhecer os diferentes tipos de apoios e quais reações eles produzem no modelo de análise. Abaixo se tem uma pequena folha de dicas dos diferentes tipos de apoios e suas reações:
| Tipo de Suporte | Tradução | Rotação | Notas |
|---|---|---|---|
Apoio engastado |
Fixo em todas as direções Reações em X,Y,Z |
Fixo em todas as direções Reações em X,Y,Z |
FFFFFF – Reações em todos os graus de liberdade |
Suporte de rolo horizontal |
Fixo em Y Reações apenas na direção Y |
Lançado em todas as direções Sem reações rotacionais |
RFFRRR – As reações são apenas na direção Y |
Suporte Fixado ou Articulado |
Fixo em X,Y,Z Reações em X,Y,Z |
Lançado em todas as direções Sem reações rotacionais |
FFFRRR – Reações em todas as traduções, nenhum em rotação |
Suporte Cantilever |
Fixo em todas as direções Reações em X,Y,Z |
Fixo em todas as direções Reações em X,Y,Z |
O mesmo que fixo |
Uma guia passo a passo sobre como determinar as reações de suporte em vigas:
Determinar as reações nos apoios é sempre o primeiro passo na análise de uma viga ou membro, e geralmente é o mais fácil. Envolve o cálculo da fórmula da força de reação e dos momentos de reação nos apoios (apoios A e B no exemplo abaixo) devido às forças que atuam na viga. A fórmula da força de reação é usada para encontrar as forças exercidas nos apoios devido às cargas que atuam na viga. Você precisará saber disso para continuar com o cálculo dos diagramas de momento fletor (BMDs) e dos diagramas de força de corte (SFDs); esta é uma parte importante que se aprende nos cursos de estática na faculdade. SkyCiv oferece uma ótima Calculadora de reações que permite modelar qualquer viga e mostrar esses cálculos manuais para você, mas também ajuda a entender o conceito envolvido.
Vídeo tutorial: Determine as reações nos apoios
Ao resolver um problema como este, queremos primeiro lembrar que a viga é estática; o que significa que não está se movendo. Da física simples, isso significa que a soma das forças na direção Y é igual a zero (Ou seja. as forças descendentes totais são iguais às forças ascendentes totais). Uma segunda fórmula a lembrar é que a soma dos momentos sobre qualquer ponto é igual a zero. Isso ocorre porque a viga é estática e, portanto, não rota.
Para determinar as reações nos apoios, siga estes passos simples:
1. Soma dos momentos (ΣM = 0)
Tudo o que precisamos saber sobre os momentos nesta fase é que eles são iguais à força multiplicada pela distância de um ponto (Ou seja. a força multiplicada pela distancia ao ponto). Considere um exemplo simples de uma viga de 4 m com um suporte fixo em A e um suporte móvel em B. O diagrama de corpo livre é mostrado abaixo, onde AY e BY são as reações verticais nos suportes: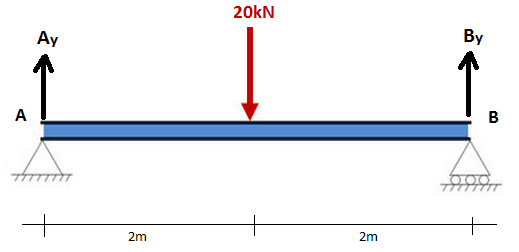
Primeiro queremos considerar a soma dos momentos em relação ao ponto B e deixá-lo igual a zero. Escolhemos o ponto B para provar que isso pode ser feito em qualquer extremidade da viga (desde que seja um suporte fixo). Contudo, você poderia facilmente trabalhar a partir do ponto A. Então, agora somamos os momentos sobre o ponto B e deixamos a soma igual 0:
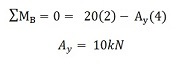
NOTA: A convenção de sinais que escolhemos é que os momentos no sentido anti-horário são positivos e os momentos no sentido horário são negativos. Esta é a convenção de sinalização mais comum, mas depende de você. Você deve SEMPRE usar a mesma convenção de sinalização em todo o problema. Sempre use a mesma convenção desde o início. Agora temos nossa primeira equação. Precisamos resolver outra equação para encontrar BY (a força de reação vertical no suporte B).
2. Soma das Forças Horizontais (ΣFY = 0)
Some as forças na direção Y (vertical) e deixe a soma igual a zero. Lembre-se de incluir todas as forças, incluindo as reações e cargas normais, como as cargas pontuais. Então, se somarmos as forças na direção Y para o exemplo acima, temos a seguinte equação:
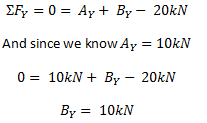
NOTA: Mais uma vez, aderimos a uma convenção de sinalização que toma as forças para cima (nossas reações) como forças positivas e as descendentes (as cargas pontuais) como negativas. Lembre-se de que a convenção de sinalização é arbitraria, mas SEMPRE deve usar a mesma convenção de sinalização em todo o problema.
Logo, nós usamos as duas equações acima (soma dos momentos igual a zero e soma das forças verticais igual a zero) e calculamos a reação no suporte A que é igual a 10 kN e a reação no suporte B que é 10kN. Isso faz sentido, pois o ponto de carga está bem no meio da viga, o que significa que ambos os suportes devem ter as mesmas forças verticais (Ou seja. o problema é simétrico).
Ao determinar as forças que atuam na viga, tanto a soma das forças quanto a soma dos momentos são usadas. A fórmula da força de reação ajuda a calcular as forças verticais e horizontais, enquanto a soma dos momentos de reação permite garantir que o feixe permaneça em equilíbrio estático.
Resumindo, aqui se presentam todos os cálculos manuais produzidos pelo SkyCiv Beam:
Software SkyCiv Beam
Através deste artigo, você aprendeu como encontrar a força de reação. O software de análise de vigas SkyCiv permite que os usuários analisem vigas com facilidade e precisão. Você pode obter uma análise das suas vigas, incluindo reações, forças de corte, momentos de flexão, deflexões, esforços, e incluso vigas indeterminadas em questão de segundos.
Se você quiser experimentar primeiro, a Calculadora de vigas grátis é uma ótima maneira de começar, ou simplesmente inscreva-se gratuitamente hoje!