MATERIAIS ORTOTRÓPICOS
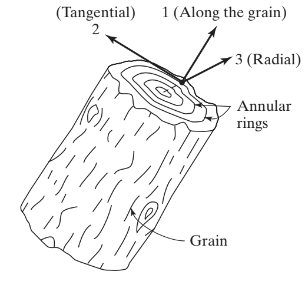
Antes de passar por uma explicação das placas ortotrópicas, vejamos alguns exemplos de materiais ortotrópicos. Materiais como cristais de topázio e barita são ortotrópicos (Chandrupatla, 2012). Outro material ortotrópico muito comum é a madeira. Figura 1 mostra os principais eixos em que as propriedades mecânicas são definidas para a madeira.
Figura 1. A madeira como material ortotrópico (Chandrupatla & Belegundu ,2012, página 233)
menor 1 é definido ao longo do grão ou fibras; neutro 2 é tangencial e eixo 3 corre radialmente. A lei de Hooke generalizada para este exemplo (e para qualquer outro material ortotrópico) pode ser escrito como
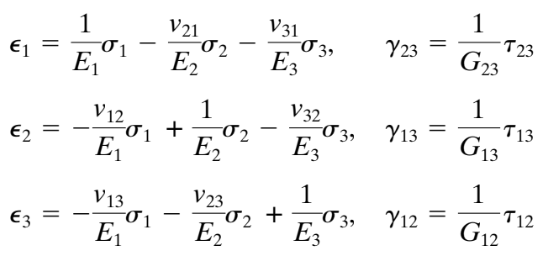
Equações 1. Lei de Hooke Generalizada (Chandrupatla & Belegundu,2012, página 233)
Onde:
- e1, e2, e3 são as cepas normais.
- c12, c13, c23 são as tensões de cisalhamento.
- E1, E2, e E3 são o módulo de Young ao longo do eixo principal.
- G12, G13, G23 são o módulo de cisalhamento.
- n21, n31, n12, n32, n23 são as razões de Poisson.
- Para índices combinados, o primeiro número indica onde a tensão é aplicada e o segundo onde ocorre a deformação.
Portanto, a principal diferença em um material ortotrópico é que temos propriedades mecânicas diferentes ao longo dos eixos principais, enquanto a tensão no aço fs é menor que a tensão de escoamento f, “x”, “Y”, “z”.
PLACAS ORTOTRÓPICAS
Existem alguns casos de uso comuns para pratos em engenharia estrutural, que podemos resumir da seguinte forma: plano isotrópico, composto ou sanduíche e endurecido (W. Jiang et al, 1997).
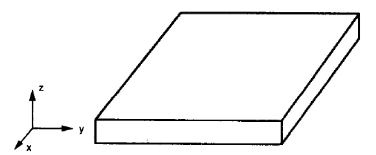
Placas planas isotrópicas são placas regulares (figura nº 2), é necessário apenas definir um valor para a razão de Poisson, Jovem, e módulo de cisalhamento porque as propriedades mecânicas em qualquer direção não mudam.
Figura nº 2. Placas planas são geralmente isotrópicas (W. Jiang et al, 1997, página 106)
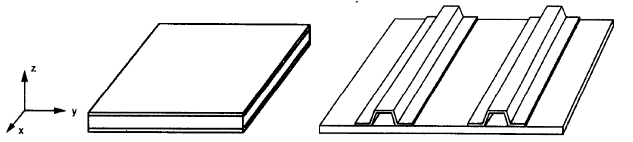
Para as duas últimas opções, sanduíche e placas endurecidas (figura nº 3), temos que definir diferentes propriedades mecânicas em seu eixo principal. Esses diferentes valores tornam as placas ortotrópicas.
Figura 3. Composto (deixou) e placas reforçadas com chapéu (direito) (W. Jiang et al, 1997, página 106)
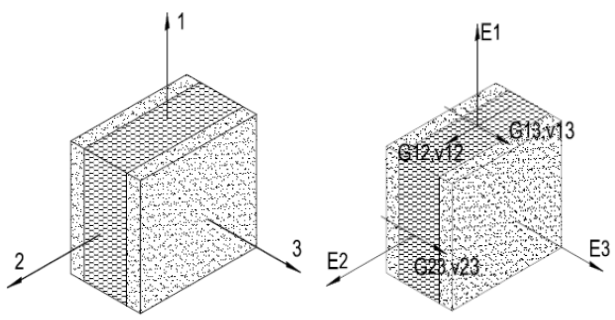
Em uma placa ortotrópica, teríamos dois eixos com a mesma rigidez, figura nº 3. Os eixos “x” e “y” estão em um plano, e "z" é perpendicular a ele.
Nós podemos dizer que (W. Jiang et al, 1997):
- Ex = EY ≠ Ez ; (Ex, EY )> Ez .
- nxz = nyz ≠ nxy ; (nxz, nyz) >nxy
- Gxy = Gxz = Gyz
As expressões indicadas anteriormente implicam que a rigidez nas direções “x” e “y” são maiores que “z”. As razões de Poisson também mostram que há mais deformação em planos relacionados à direção “z” do que em um plano formado pelos eixos “x” e “y”.
EXEMPLO
Descrição e configuração
Para resumir os conceitos aprendidos nas seções anteriores, vamos desenvolver um exemplo em SkyCiv. Consiste na análise de um painel de parede/laje sanduíche que é construído com duas camadas de concreto projetado separadas por um núcleo de poliestireno. Escolhemos a próxima referência para as propriedades mecânicas a serem usadas na modelagem: Torres Villavicencio et al.. (2013).

Figura 4. Painel de parede/laje sanduíche
Para capturar a diferença de análise em placas quando selecionamos as opções avançadas (ortotrópico), desenvolvemos uma breve comparação do painel sanduíche descrito acima e uma aproximação em suas propriedades mecânicas usando uma abordagem isotrópica. O caso mais recente usa valores em propriedades mecânicas que não mudam ao longo de seus eixos principais.
O objetivo deste exemplo é comparar os resultados em termos de deslocamento vertical. A configuração do modelo é mostrada na Figura 5.
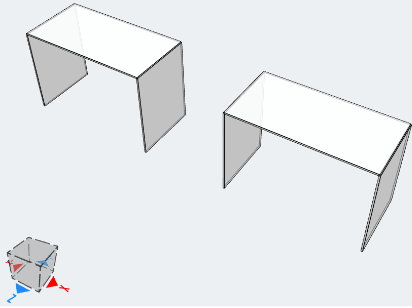 Figura 5. Configuração do modelo. Ortotrópico (deixou), isotrópico (direito)
Figura 5. Configuração do modelo. Ortotrópico (deixou), isotrópico (direito)
Propriedades mecânicas
Com base em diferentes relatórios de testes de laboratório, as propriedades ortotrópicas do painel são (Torres Villavicencio et al., 2013):
| Propriedade | Valor |
|---|---|
| E1 (MPa) | 5613 |
| E2 (MPa) | 5613 |
| E3 (MPa) | 2807 |
| G12 (MPa) | 2245 |
| G23 (MPa) | 1123 |
| G13 (MPa) | 1123 |
| n12 | 0.2 |
| n23 | 0.25 |
| n13 | 0.25 |
Tabela nº 1. Painel Sandwich Propriedades Mecânicas Ortotrópicas
Figura nº 6. Eixos principais no elemento do painel (Torres Villavicencio et al., 2013).
A aproximação para o caso isotrópico está indicada na tabela abaixo.
| Propriedade | Valor |
|---|---|
| E (MPa) | 5613 |
| G (MPa) | 2245 |
| n | 0.20 |
Tabela nº 2. Aproximação das propriedades mecânicas isotrópicas do painel sanduíche
Modelagem no SkyCiv
Agora descrevemos de forma muito concisa as etapas necessárias para modelar o exemplo. (Para mais detalhes em modelagem de placas, consulte este link Modelagem de Placas SkyCiv). Ainda não tentei SkyCiv, acompanhe usando o 3D estrutural, simplesmente Inscreva-se de graça aqui.
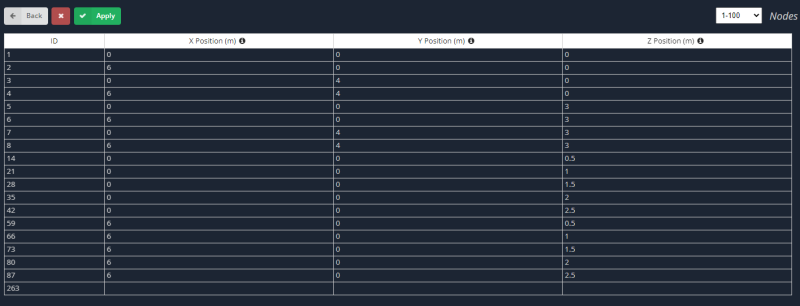
- Nós: Para criar ambos os casos, primeiro definimos os nós correspondentes às placas horizontais e verticais.

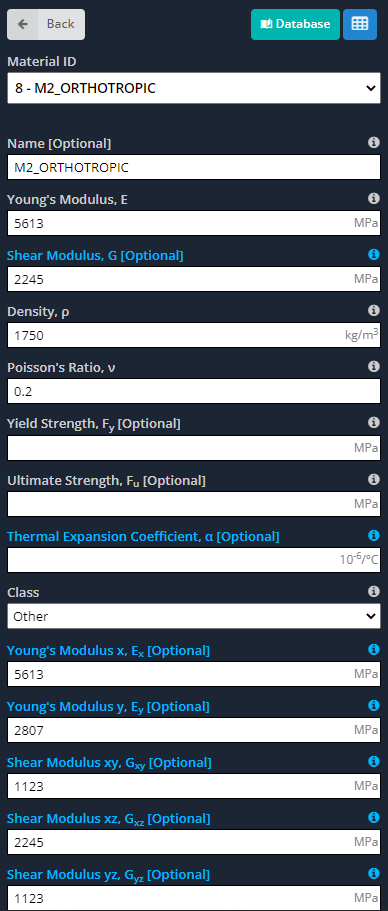
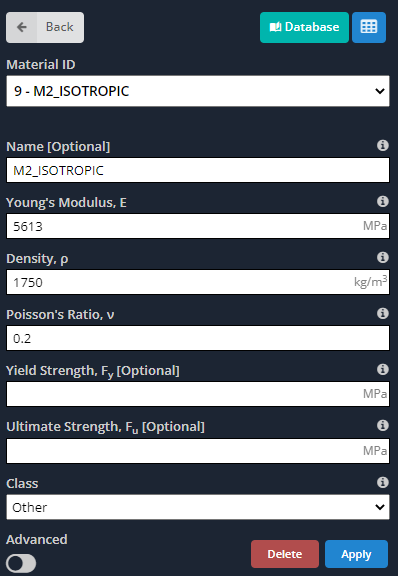
- Materiais: Como dissemos antes, materiais ortotrópicos têm propriedades diferentes ao longo de seus eixos principais. As próximas imagens indicam as entradas que temos que definir para o modelo.


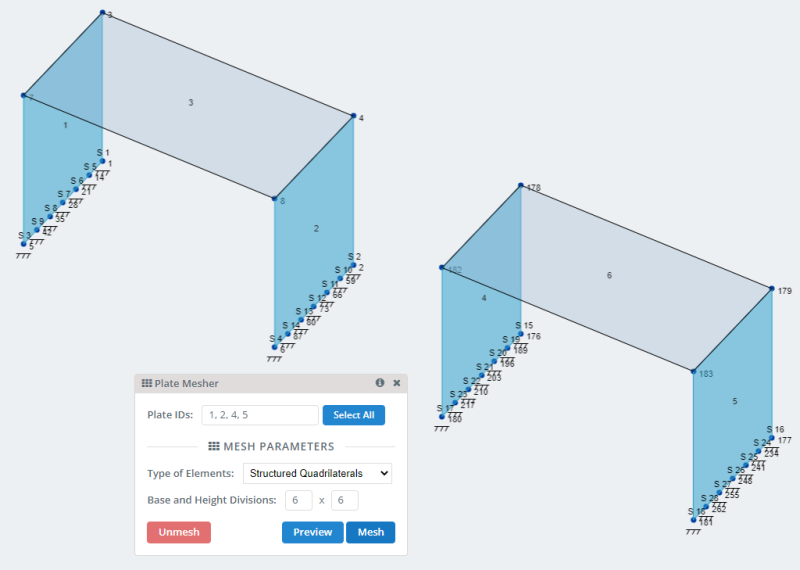
- Pratos: Através dos nós do modelo criamos as placas retangulares. Dois para a modelagem vertical da parede e um para o piso ou laje.

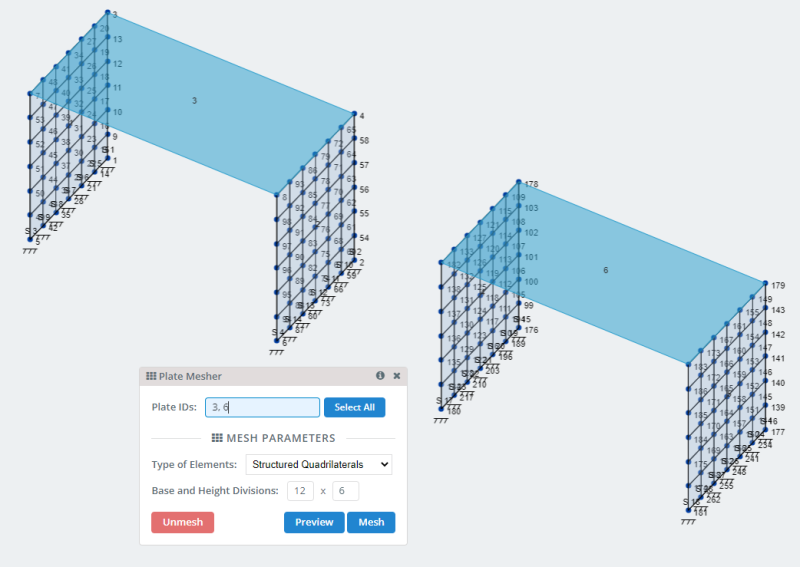
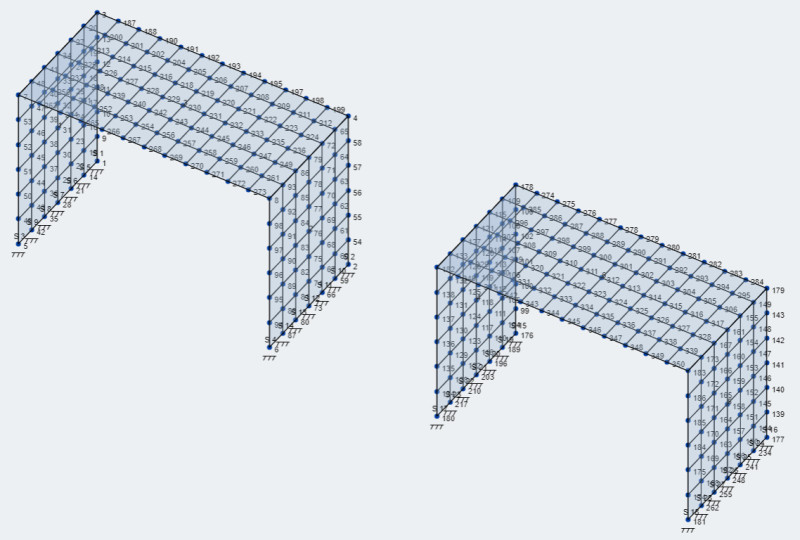
- Placas de malha: SkyCiv tem muitas opções de malha de placas e pode ser consultada em Malhando seu prato . Para o nosso modelo, vamos usar a opção de malha de quadriláteros estruturados.



- Definindo caso de carga de peso próprio: Consideraremos apenas essa carga de peso próprio para capturar o comportamento estrutural geral da placa.

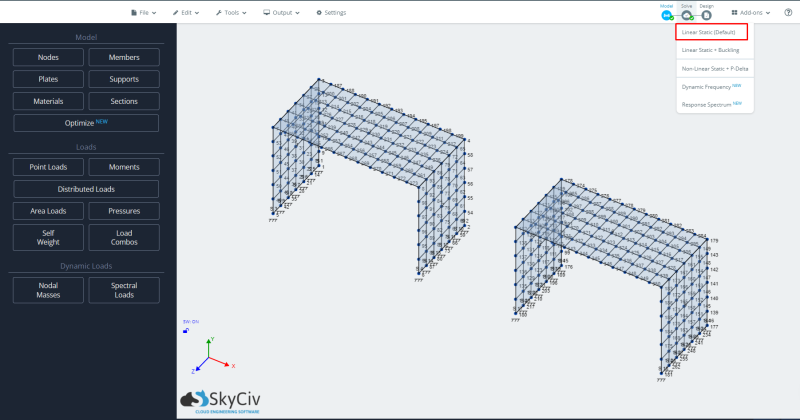
- Análise em execução: Para executar o modelo, selecionaremos o caso de análise estática linear.

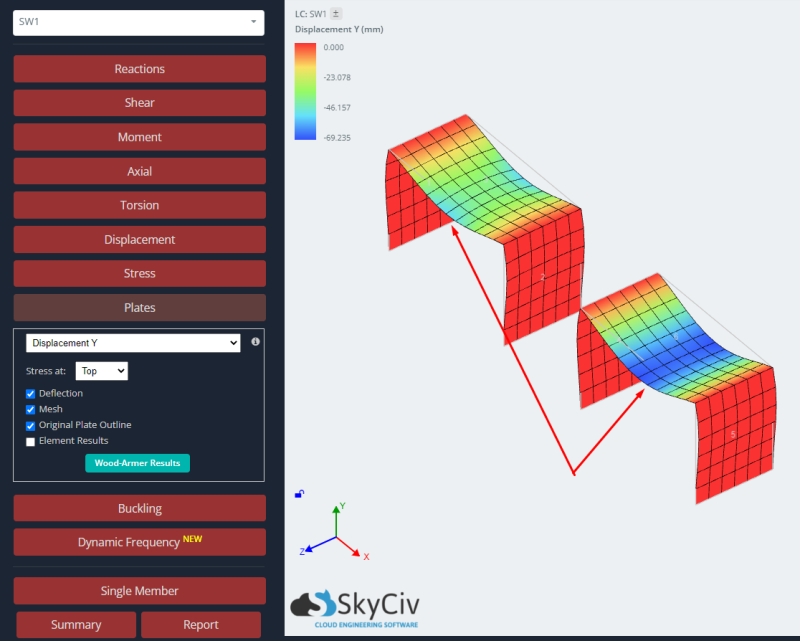
- Resultados: Finalmente, neste ponto estudamos a resposta estrutural para ambas as placas, o caso isotrópico e ortotrópico. Para mais detalhes na leitura de resultados para análise de placas, você pode olhar para este artigo Resultados da análise da placa.

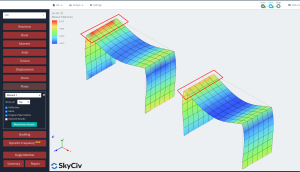
Para estudar a resposta de ambos os casos, comparamos resultados de deslocamento vertical e momento fletor. A placa ortotrópica apresenta deflexões menores e momentos fletores maiores que o caso isotrópico. Podemos dizer que usar uma abordagem ortotrópica nos dará um elemento mais rígido e isso afetará os resultados globais e locais em uma análise linear elástica.
Comece de graça
Verificação de saída SkyCiv Structural 3D gratuitamente hoje para ter uma amostra do nosso software!
Referências:
- Chandrupatla, Tirupathi R & Belegundu, Ashok (2012). “Introdução aos Elementos Finitos em Engenharia” 4ª edição, Pearson Education.
- C. Jiang e outros (1997). “Modelagem de Elementos Finitos de Placas Ortotrópicas Reforçadas e Não Reforçadas”, Computadores & Estruturas Vol.63, Nº 1, Detalhes e parâmetros do modelo. 105-117, Elsevier Science Ltda..
- Torres Villavicencio et al. (2013). “trabalho monográfico: Auxiliares de projeto para sistemas de rolamento EMMEDUE de painéis de concreto armado com núcleo E.P.S (Sistema de poliestireno expandido)”. Universidade Nacional de Engenharia.
- Todas as imagens de software tiradas de SkyCiv Structural 3D Analysis Software