Um exemplo totalmente trabalhado de NBCC 2015 cálculos de carga de neve
O acúmulo de neve nas estruturas pode ser muito perigoso para os membros do telhado ou outros elementos estruturais expostos. A Código Nacional de Construção do Canadá (2015) Divisão B – Seção 4.1.6 fornece um cálculo detalhado das cargas de neve e as cargas de chuva associadas. Usando esta diretriz, vamos demonstrar como calcular as cargas de neve usando um exemplo Structural 3D (S3D) modelo de armazém, como mostrado abaixo:
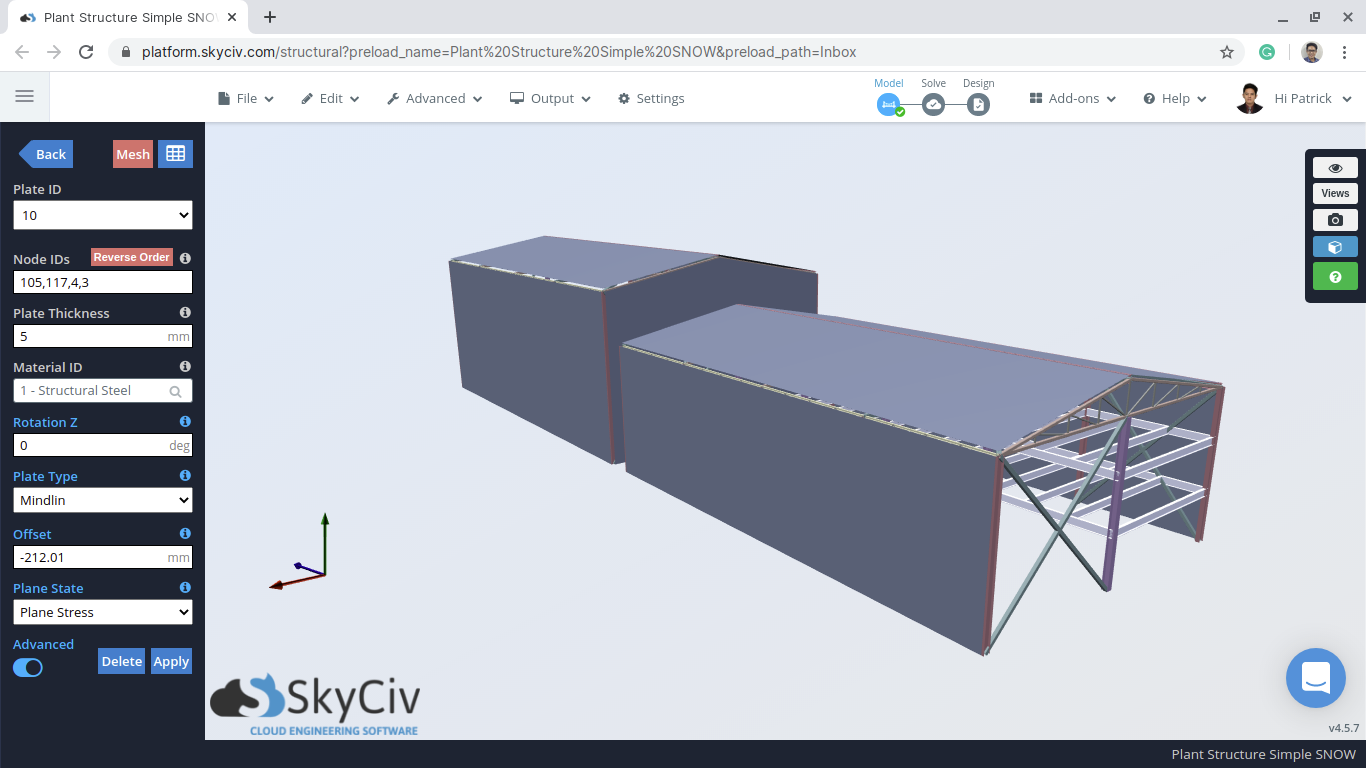
Figura 1: Exemplo de modelo de armazém S3D
Figura 2: Exemplo de localização de site usando o Google Maps (apenas para ilustração).
Tabela 1: Dados de construção necessários para nosso cálculo de carga de neve.
| Localização | Ogden, Calgary, Alberta (apenas para ilustração) |
| Ocupação | Armazém ou armazenamento de materiais |
| Dimensões | 19.508 m x 31.70 m para cada estrutura Altura da beirada do prédio menor 9.144 m Altura do ápice de construção menor 11.941 m A diferença de telhado superior e inferior é 3.50 m Ângulo de inclinação do telhado 16° |
| detalhes adicionais | O telhado tem uma superfície escorregadia A lacuna entre as estruturas é 2.30 m |
Da mesa 1, a carga de neve especificada, \(S ), pode ser calculado usando a fórmula:
\(S = {I}_{s}[{S}_{s}{C}_{b}{C}_{C}{C}_{s}{C}_{uma} +{S}_{r}]\) (1)
Onde:
\({I}_{s}\) = fator de importância para a carga de neve, Tabela 4.1.6.2-A
\({S}_{s}\) = 1-carga de neve no solo em 50 anos, kPa , Subseção 1.1.3
\({C}_{b}\) = fator de carga básico da neve do telhado, 4.1.6.2 (2)
\({C}_{C}\) = fator de exposição ao vento baseado, 4.1.6.2 (3) e (4)
\({C}_{s}\) = fator de inclinação, 4.1.6.2 (5), (6), e (7)
\({C}_{uma}\) = fator de acumulação, 4.1.6.2 (8)
\({S}_{r}\) = Carga de chuva associada de 1 em 50 anos, kPa , Subseção 1.1.3, mas não maior que \({S}_{s}{C}_{b}{C}_{C}{C}_{s}{C}_{uma}\)
Cada parâmetro será examinado individualmente nas seguintes seções. Os seguintes casos de carga de neve serão calculados: carga de neve equilibrada e desequilibrada em cada telhado (vento normal para crista), bem como a deriva gerada no telhado inferior considerando o acúmulo de deslizamento.
Fator de Importância, \({I}_{s}\)
A primeira coisa que é determinada é o fator de importância, \({I}_{s}\), que é encontrado usando Tabela 4.1.6.2-A como referenciado. Por se tratar de um edifício de armazenamento que tem baixo impacto direto na vida humana em caso de falha, a categoria de importância é Baixo. Além disso, o cálculo será no estado limite máximo (ULS). Então de Tabela 4.1.6.2-A, \({I}_{s}\) é igual a 0.80.
| Categoria de Importância | Fator de Importância, \({I}_{s}\) | |
|---|---|---|
| ULS | SLS | |
| Baixo | 0.8 | 0.9 |
| Normal | 1.0 | 0.9 |
| Alto | 1.15 | 0.9 |
| Pós-desastre | 1.25 | 0.9 |
Carga de neve no solo, \({S}_{s}\), e carga de chuva associada, \(({S}_{r})\)
A carga de neve no solo, \({S}_{s}\), e carga de chuva associada, \(({S}_{r})\), os valores são tabulados em apêndice C, Divisão B de NBCC 2015 dependendo da localização e província. Para este exemplo, o correspondente \({S}_{s}\) e \(({S}_{r})\) no Calgary, Alberta é igual a 1.10 kPa e 0.1 kPa , respectivamente.
Tendo dificuldade em pesquisar a neve do solo e a carga de chuva associada para NBCC 2015? Tentar a Ferramenta Geradora de Carga Gratuita SkyCiv para acelerar sua pesquisa e obter o correspondente \({S}_{s}\) e \({S}_{r}\) com base na localização de sua estrutura.
Fator de Exposição ao Vento, \({C}_{C}\)
Para o fator de exposição ao vento, \({C}_{C}\), deve ser permitido ser igual a 1.0 baseado em 4.1.6.2 (3). Este fator ainda pode ser reduzido, desde que as condições em 4.1.6.2 (4) é satisfeito. Para este exemplo, \({C}_{C}\) deve ser igual a 1.0 uma vez que o local não é um terreno aberto que expõe totalmente a estrutura ao vento.
Fator básico de carga de neve no telhado, \({C}_{b}\)
O fator de carga básico da neve do telhado, \({C}_{b}\), pode ser calculado usando as seguintes fórmulas, como referenciado em 4.1.6.2 (2):
\({C}_{b} = 0.8\) (2) pra \({eu}_{c} ≤ (70/{{C}_{C}}^{2})\) e
\({C}_{b} = (1/{C}_{C}) [1 – (1 – 0.8{C}_{C})exp(-0.01({eu}_{c}{{C}_{C}}^{2} – 70))] \) (3) pra \({eu}_{c} > (70/{{C}_{C}}^{2})\)
Onde:
\({eu}_{c}\) = comprimento característico do telhado superior ou inferior definido como: \(2C -{C}^{2}/eu)
\(eu) = maior dimensão do plano do telhado
\(w\) = menor dimensão do plano do telhado
Para este exemplo,\(eu) e \(w\) é igual a 31.7 me 19.51 m, respectivamente, por isso, \({eu}_{c}\) é igual a 27.01. Desde a \({eu}_{c}\) é menos do que \((70/{1.0}^{2})\), o fator de carga básico da neve do telhado, \({C}_{b}\), é igual a 0.8.
Fator de inclinação, \({C}_{s}\)
O cálculo do fator de inclinação é \({C}_{s}\) detalhado em 4.1.6.2 (5), (6), e (7) é mostrado abaixo.
Para telhado escorregadio desobstruído:
\({C}_{s} = 1.0\) pra \(α ≤ 15°\)
\({C}_{s} = 0\) pra \(uma > 60°\)
\({C}_{s} = (60° – uma)/45°\) pra \(15° < α ≤ 60°\)
Para outros casos:
\({C}_{s} = 1.0\) pra \(α ≤ 30°\)
\({C}_{s} = 0\) pra \(uma > 70°\)
\({C}_{s} = (70° – uma)/40°\) pra \(30° < α ≤ 70°\)
Peso Específico da Neve, \(γ\)
O peso específico da neve é especificado em 4.1.6.13 e deve ser tomado como:
\(γ = 0.43{S}_{s} + 2.2 kN /{m}^{3} ≤ 4,0kN /{m}^{3}\) (4)
Para este exemplo, \(γ\) é igual a \(2.673 kN /{m}^{3}\).
Fator de Acumulação, \({C}_{uma}\)
Fator de acumulação, \({C}_{uma}\), W W 4.1.6.2 (8). W.
Carga de neve especificada, \(S )
Nesta secção, a carga de neve especificada, \(S ), será calculado para os casos balanceados e desviados.
Caixa Equilibrada / Não Encaminhada
Para o caso equilibrado / não inclinado, a fator de acumulação \({C}_{uma}\) é igual a 1.0. Além disso, W \(α\) é \(16°\) e a superfície do telhado é considerada desobstruída e escorregadia, o fator de inclinação, \({C}_{s}\), pois nosso exemplo é igual a 0.978. Usando a equação (1), a carga de neve especificada, \(S ), para o caso equilibrado / não classificado é:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
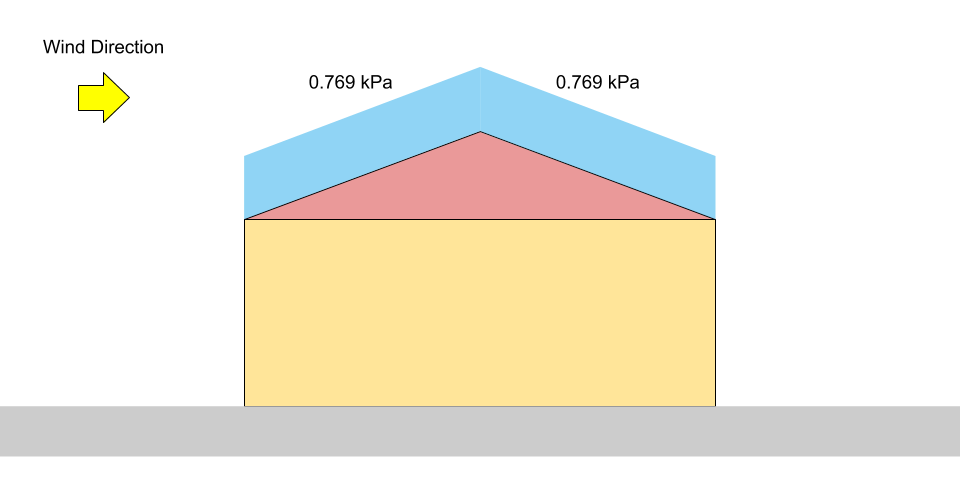
Figura 3: Diagrama de carga para carga de neve equilibrada em um telhado de duas águas.
Caixa Desequilibrada / Desviada
Vento agindo normal para cume
Uma vez que as estruturas têm telhados de duas águas, a carga de neve desequilibrada (vento agindo normal para o cume) fator de acumulação \({C}_{uma}\) é encontrado usando 4.1.6.9:
\({C}_{uma, contra o vento} = 0\)
\({C}_{uma, a favor do vento} = 0.25 +α / 20 ) pra \(15° ≤ α ≤ 20°\)
\({C}_{uma, a favor do vento} = 1.25\) pra \(20° < α ≤ 90°\)
Porque ambas as estruturas têm ângulo de inclinação do telhado igual a 16 °, os fatores de acumulação \({C}_{uma, contra o vento}\) e \({C}_{uma, a favor do vento}\) são iguais a 0 e 1.05, respectivamente. Além disso, W \(α\) é \(16°\) e a superfície do telhado é considerada desobstruída e escorregadia, o fator de inclinação, \({C}_{s}\), pois nosso exemplo é igual a 0.978.
No caso desequilibrado / desviado normal para o cume, \({C}_{uma}\) deve ser calculado com base em 4.1.6.9 para um caso de telhado de duas águas. Do cálculo acima, \({C}_{uma, contra o vento} = 0\) e \({C}_{uma, a favor do vento} = 1.05\). Conseqüentemente, as cargas de neve especificadas para cada lado são:
\({S}_{contra o vento} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S}_{a favor do vento} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)
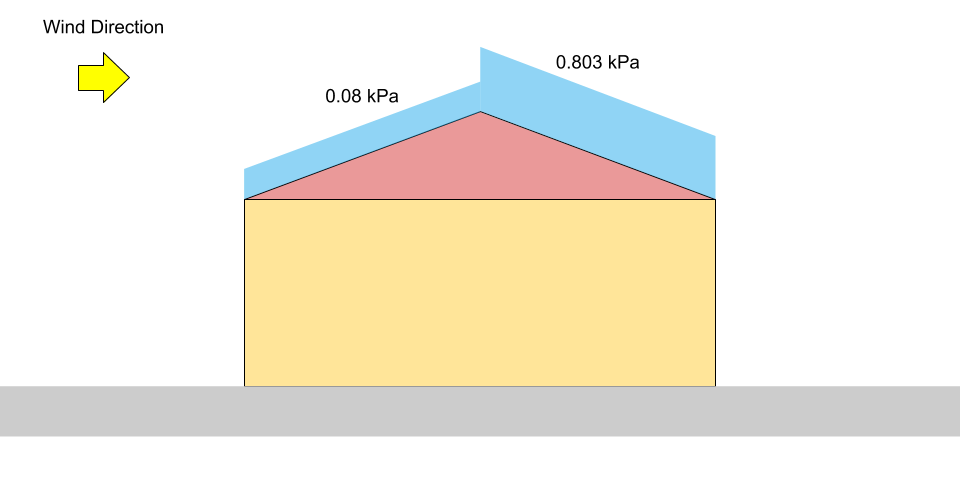
Figura 4: Diagrama de carga para carga de neve desequilibrada em um telhado de duas águas (não escalar).
Vento atuando paralelamente ao cume – Caso I – Vento do telhado superior para o inferior
Quando o vento está agindo paralelo ao cume, um monte de neve provavelmente será desenvolvido no telhado inferior. W fator de acumulação \({C}_{uma}\), as seguintes fórmulas de 4.1.6.2 (8) são usados:
\({C}_{uma} ={C}_{a0} – ({C}_{a0} – 1)(x /{x}_{d})\) pra \(0 ≤ x ≤ {x}_{d}\)
\({C}_{uma} = 1.0\) pra \(x > {x}_{d}\)
Onde:
\({C}_{a0}\) = valor de pico de \({C}_{a0}\) em x = 0
\(x\) = distância do degrau do telhado
\({x}_{d}\) = comprimento de deriva conforme mostrado na Figura 3 abaixo
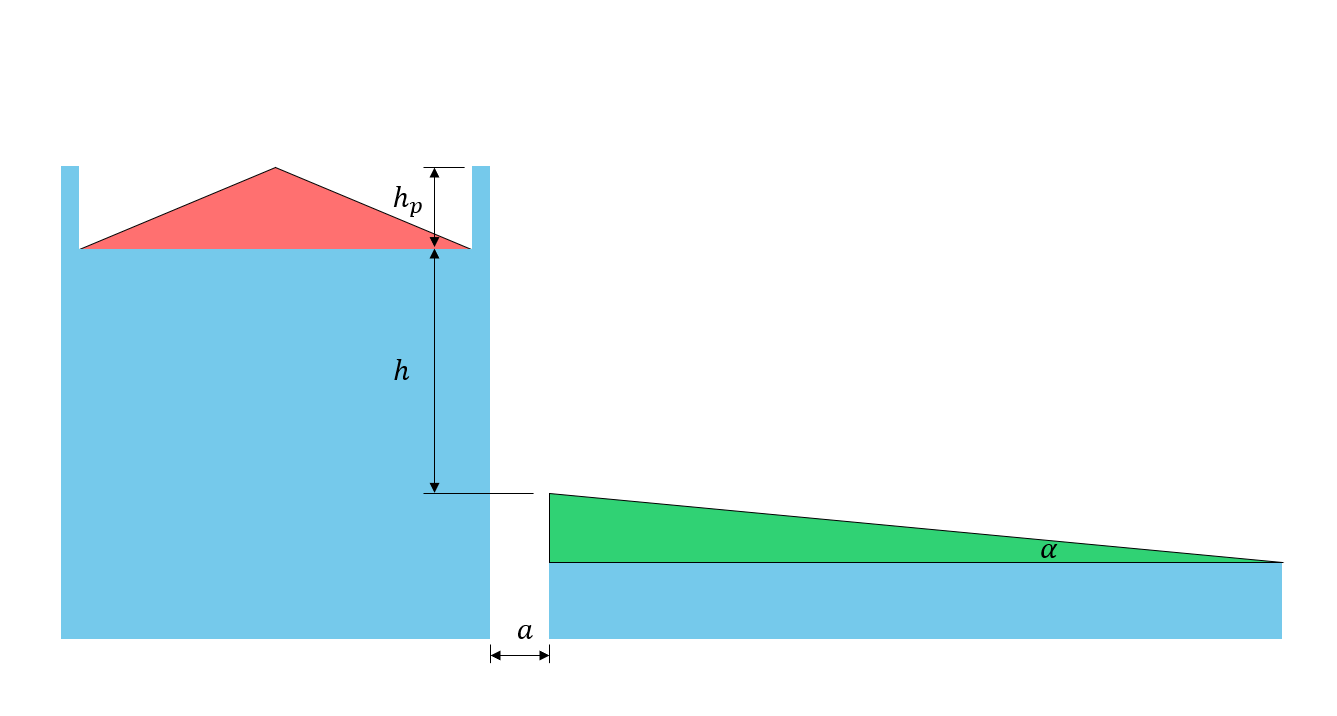
Figura 5: Ilustração dos parâmetros de dimensão do telhado
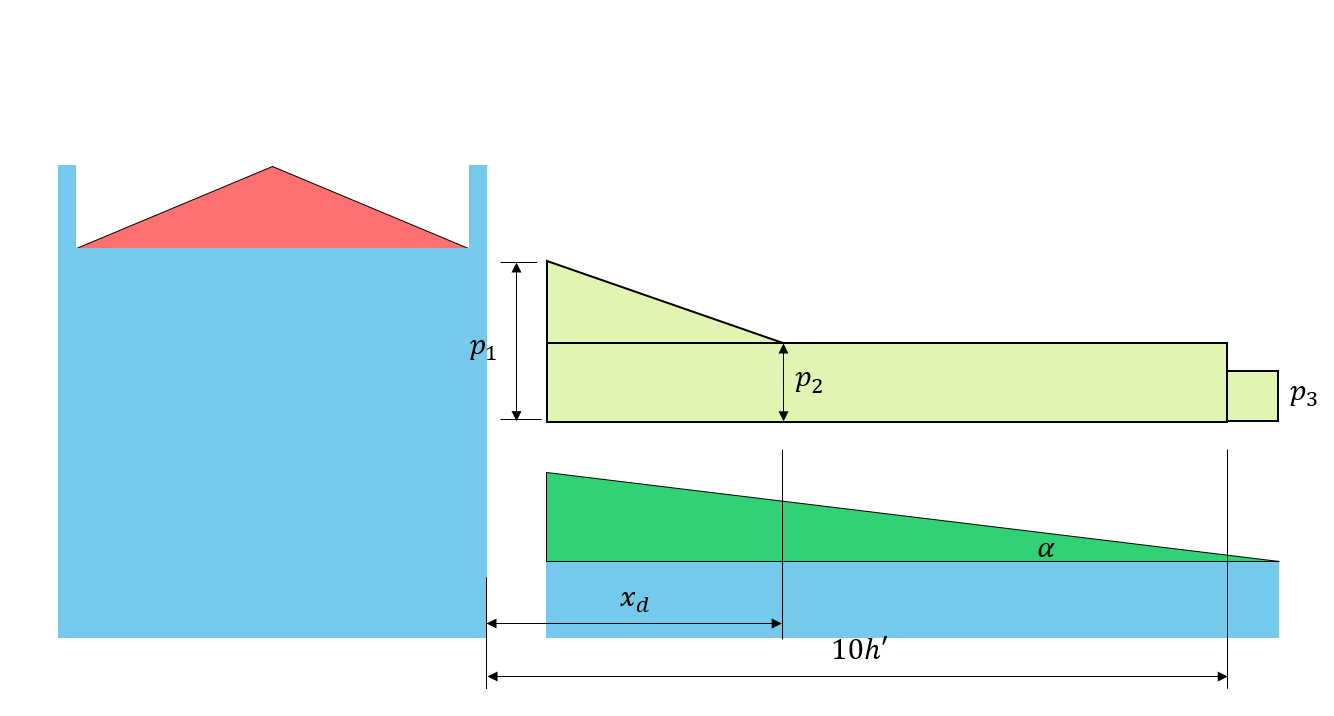
Figura 6: Carga de deriva correspondente no telhado inferior com base em Figura 4.1.6.5-A.
\({C}_{a0}\) e \({x}_{d}\) pode ser calculado usando as seguintes fórmulas:
\({C}_{a0} = frac{βγh}{{C}_{b}{S}_{s}}\) ou \({C}_{a0} = frac{F}{{C}_{b}}\) (5), o que for menor
\({x}_{d} = 5 \fratura{{C}_{b}{S}_{s}}{c}({C}_{a0} – 1)\) (6)
\(F = 0.35β sqrt{\fratura{c({eu}_{cs} – 5{{h}_{p}}^{‘})}{{S}_{s}}} +{C}_{b}\) mas \(F ≤ 5\) pra \({C}_{ws} = 1.0\) (7)
\({h}^{‘} = h – \fratura{{C}_{b}{C}_{C}{S}_{s}}{c}\) (8)
\({{h}_{p}}^{‘} ={h}_{p} – \fratura{0.8{S}_{s}}{c}\) mas \(0 ≤ {{h}_{p}}^{‘} ≤ frac{{eu}_{cs}}{5}\) (9)
Onde:
\({h}_{p}\) = altura do parapeito no telhado superior (0 neste caso, uma vez que não há parapeito)
\(h ) = diferença de altura entre o nível do telhado superior e inferior
\({C}_{ws}\) = valor de \({C}_{C}\) aplicável à fonte de deriva
\({eu}_{cs}\) = comprimento característico da área de origem definida como: \(2{C}_{s} -{{C}_{s}}^{2}/{eu}_{s}\)
\({eu}_{s}\) = maior dimensão do plano da área de origem, conforme mostrado na Figura 7 e 8, mostrado abaixo
\({C}_{s}\) = menor dimensão do plano da área de origem, conforme mostrado na Figura 7 e 8, mostrado abaixo
\(β ) = 1.0 para o caso I, e 0.67 para os casos II e III.
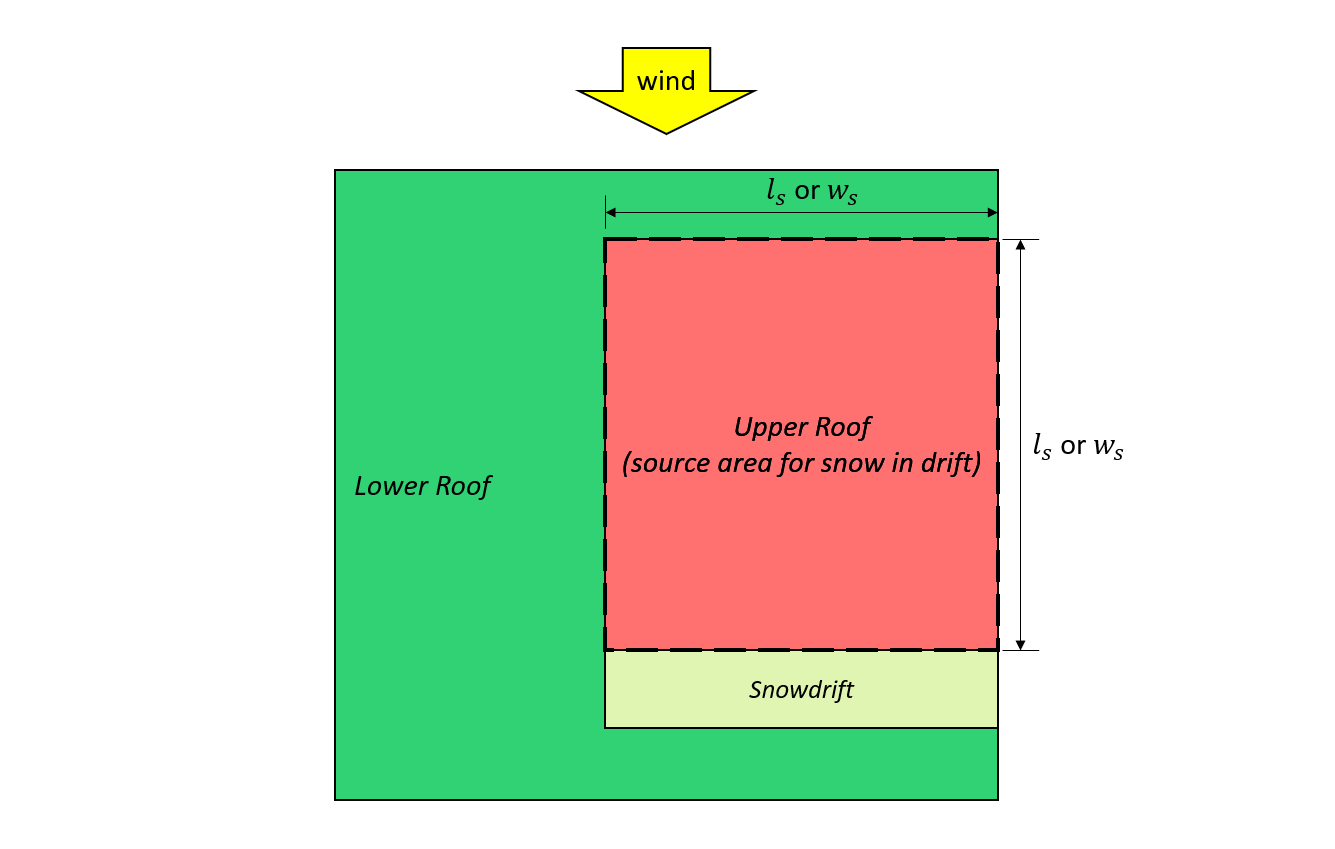
Figura 7: Caso I – monte de neve formado a partir do vento vindo do telhado superior com base em Figura 4.1.6.5-B.
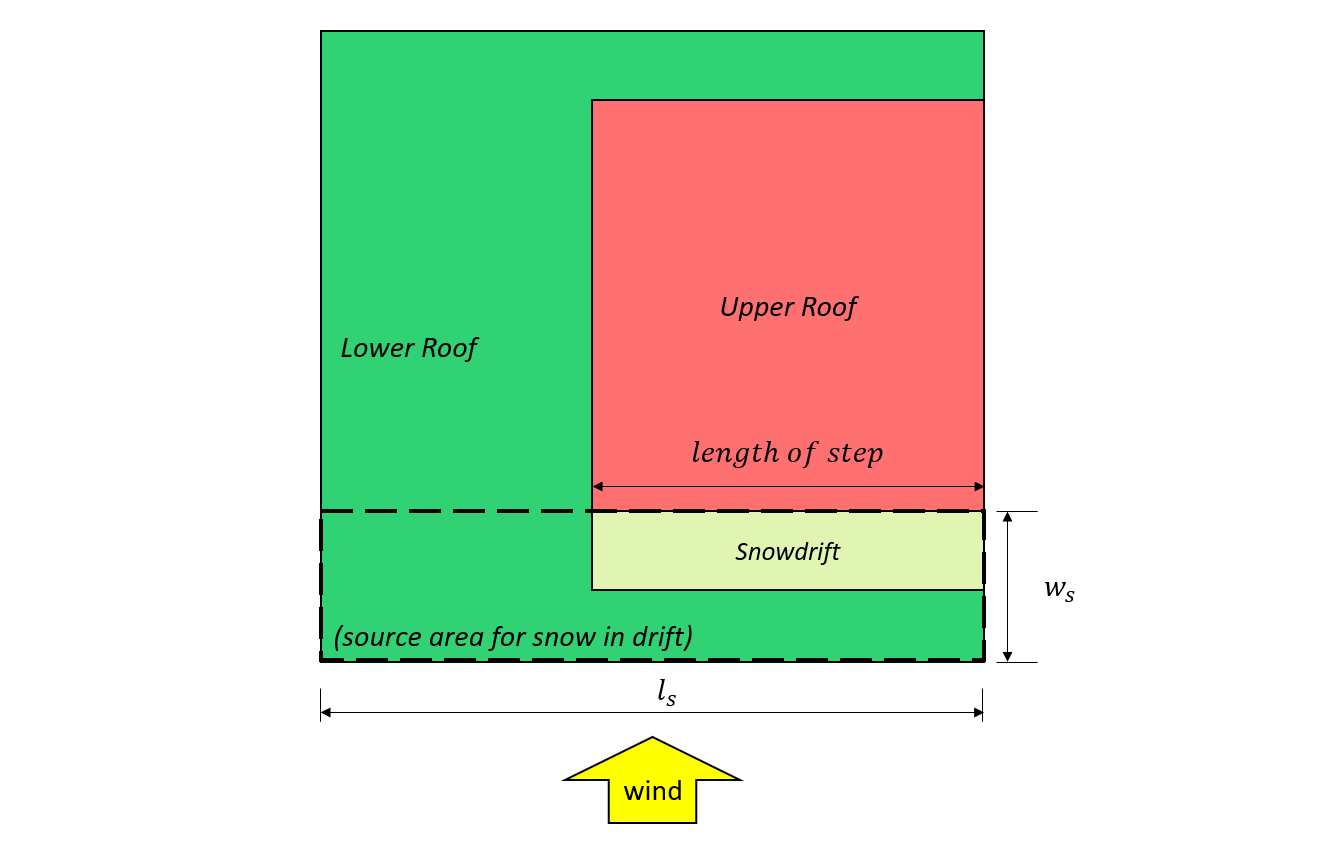
Figura 8: Caso II – monte de neve formado a partir do vento vindo do telhado inferior com base em Figura 4.1.6.5-B.
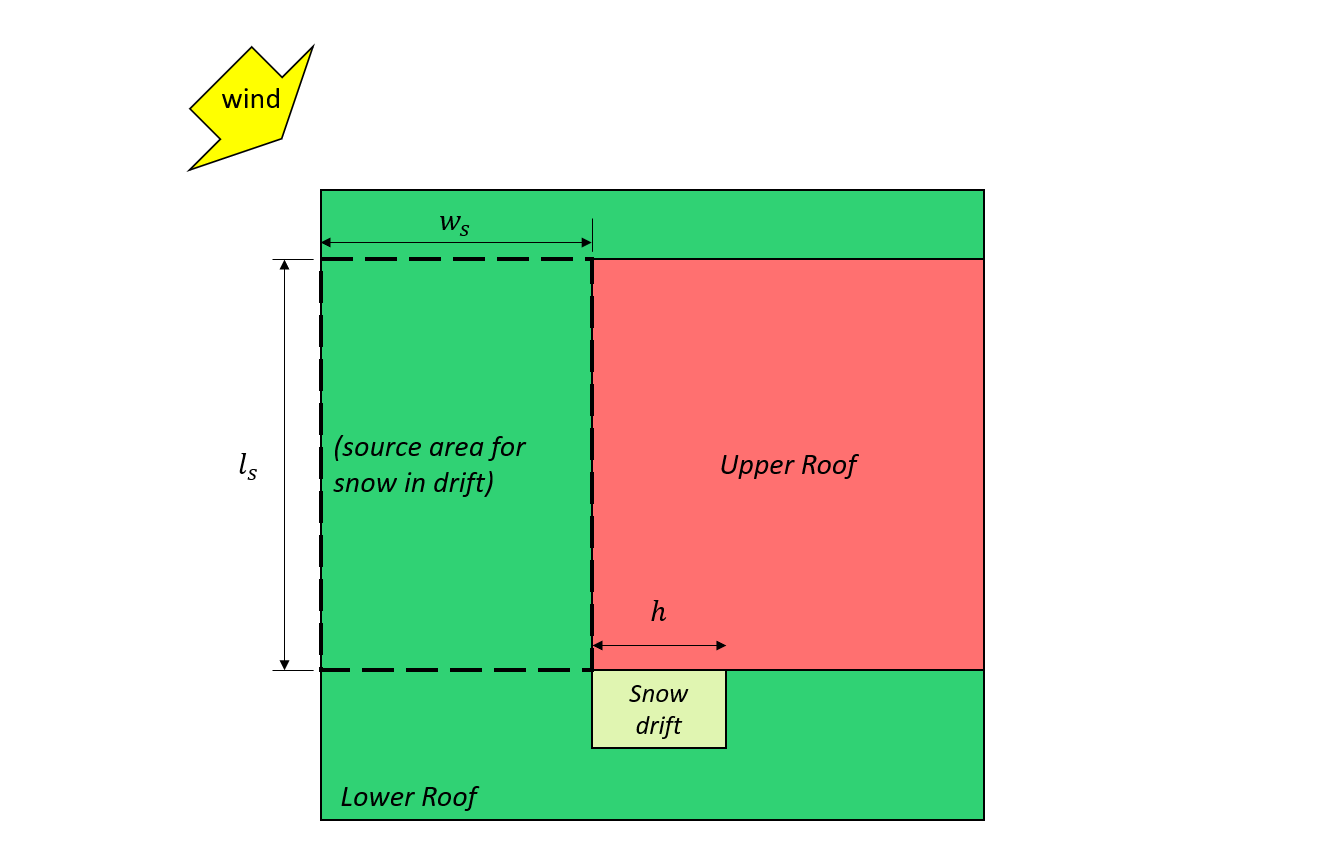
Figura 7: Caso III – monte de neve parcial formado a partir do vento vindo do telhado inferior com base em Figura 4.1.6.5-B.
Para este exemplo, Casos I e II serão considerados.
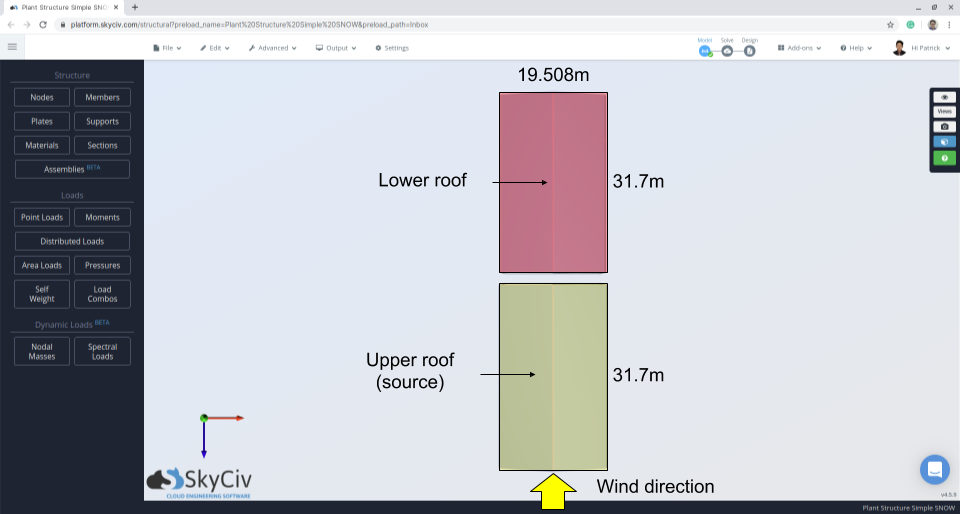
Figura 10: Plano de estrutura indicando a direção do vento e área de origem.
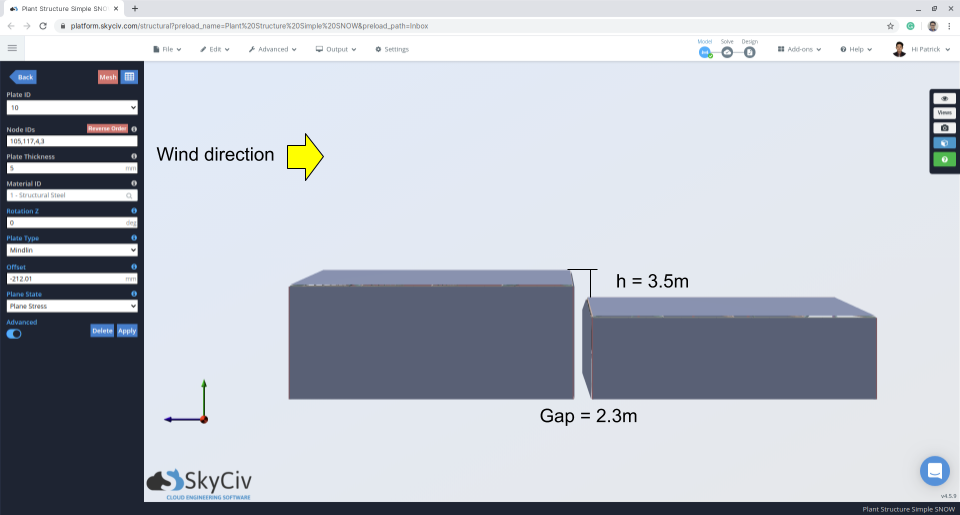
Figura 11: Vista de elevação indicando lacuna e diferença de telhado superior e inferior.
Para o caso desequilibrado / desviado paralelo ao cume, \({C}_{uma}\) deve ser calculado para o Caso I e Caso II com base em 4.1.6.5 para o telhado de vários níveis. Para o caso I, esses parâmetros a seguir devem primeiro ser calculados usando as várias equações mencionadas anteriormente neste exemplo:
\(β = 1.0\)
\({h}^{‘} = (3.5) – \fratura{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m )
\({h}_{p} = 0\)
\({{h}_{p}}^{‘} =0\)
\({eu}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m )
\(F = 0.35(1.0)\sqrt{\fratura{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) ou \({C}_{a0} = frac{3.66}{0.8} = 4.544\)
\({C}_{a0} = 4.544\)
\({x}_{d} = 5 \fratura{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 m )
A partir desses parâmetros, o fator de acumulação, \({C}_{uma}\), pode ser calculado substituindo o valor de \({C}_{a0}\) em cada \(x\) distância. Observe que precisamos calcular \({C}_{uma}\) no \(x = a ) Onde \(uma) é a lacuna entre o telhado, uma vez que a lacuna do telhado é menor que 5 m conforme especificado em 4.1.6.6.
no \(x = 0\): \({C}_{uma} = 4.544 – (4.544 – 1)(0/5.835) = 4.544\)
no \(x = a ): \({C}_{uma} = 4.544 – (4.544 – 1)(2.3/5.835) = 3.147\)
no \(x = {x}_{d}\): \({C}_{uma} =1.0\)
no \(x = 10{h}^{‘}\): \({C}_{uma} =1.0\)
W W W, \({C}_{s} = 1.0\). Além disso, ao encontrar a carga de neve especificada no telhado superior, o fator de acumulação, \({C}_{uma}\), e fator de inclinação, \({C}_{s}\), são ambos iguais a 1.0. Conseqüentemente, a magnitude das cargas de neve especificadas em cada local são:
no \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa )
no \(x = a ): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
no \(x = {x}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
no nível superior do telhado: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa )
Vento atuando paralelamente ao cume – Caso II – Vento do telhado inferior para o superior
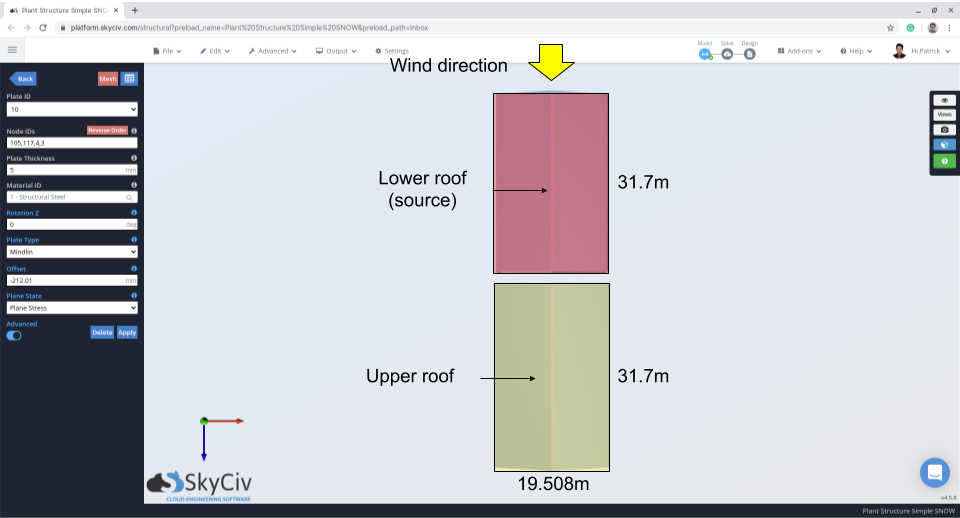
Figura 12: Plano de estrutura indicando a direção do vento e área de origem – vento do telhado inferior para o superior.
Para o Caso II, o cálculo é semelhante ao Caso I, mas tem um diferente \(β = 0.67\):
\(β = 0.67\)
\({h}^{‘} = (3.5) – \fratura{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m )
\({h}_{p} = 0\)
\({{h}_{p}}^{‘} =0\)
\({eu}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m )
\(F = 0.35(0.67)\sqrt{\fratura{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) ou \({C}_{a0} = frac{2.70}{0.8} = 3.375\)
\({C}_{a0} = 3.375\)
\({x}_{d} = 5 \fratura{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 m )
no \(x = 0\): \({C}_{uma} = 3,375 – (3.375 – 1)(0/3.909) = 3.375\)
no \(x = a ): \({C}_{uma} = 3,375 – (3.375 – 1)(2.3/3.909) = 1.978\)
no \(x = {x}_{d}\): \({C}_{uma} =1.0\)
no \(x = 10{h}^{‘}\): \({C}_{uma} =1.0\)
no \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa )
no \(x = a ): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
no \(x = {x}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
no nível superior do telhado: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa )
Para ilustração, o correspondente \({p}_{1}\), \({p}_{2}\), e \({p}_{3}\) são mostrados nas figuras 13 e 14 abaixo para os Casos I e II, respectivamente.
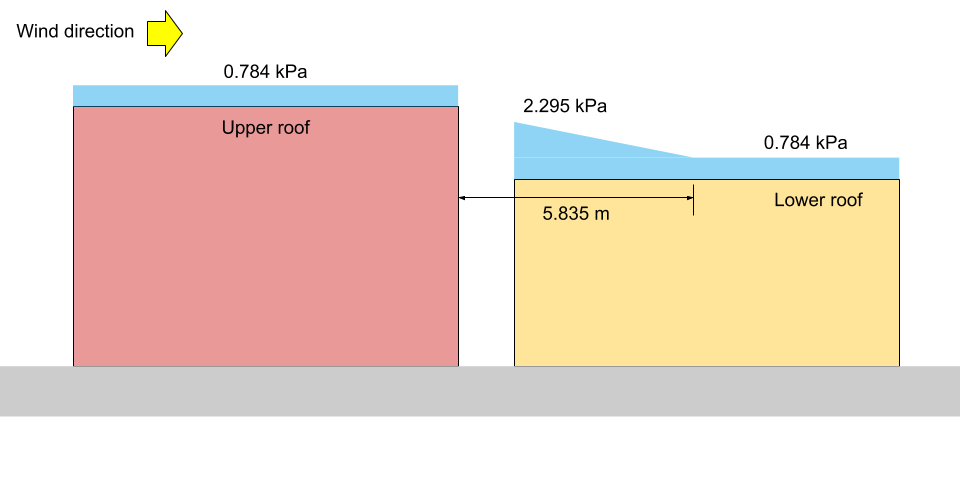
Figura 13: Ilustração de carga de neve para o caso I (não escalar).
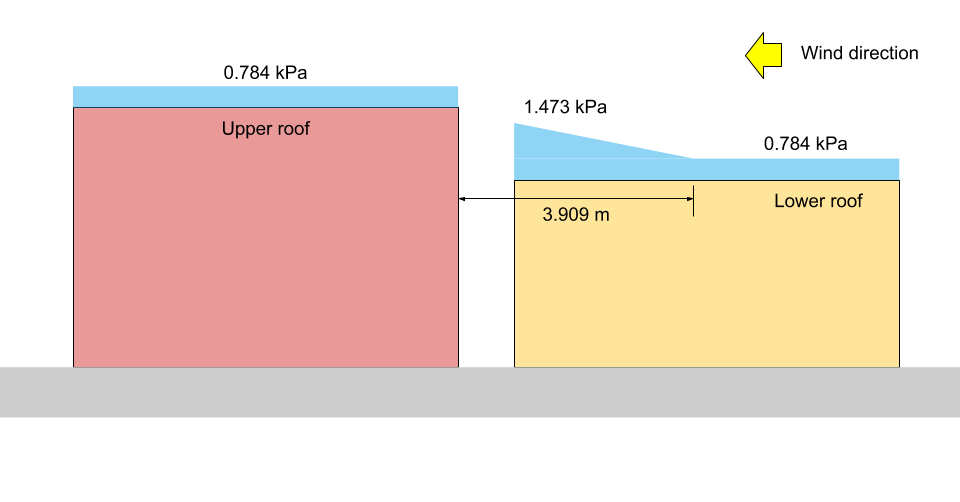
Figura 14: Ilustração de carga de neve para o caso II (não escalar).
Conclua esses cálculos automaticamente em minutos
Esse foi um cálculo longo, o que você pode fazer como engenheiro para acelerar este processo para seus projetos futuros? Recentemente, a SkyCiv lançou e automatizou o gerador de carga de neve como parte do SkyCiv Load Generator, que também pode gerar cargas de vento. Para encontrar as cargas de neve do exemplo mostrado, bastam alguns cliques para usar a ferramenta:
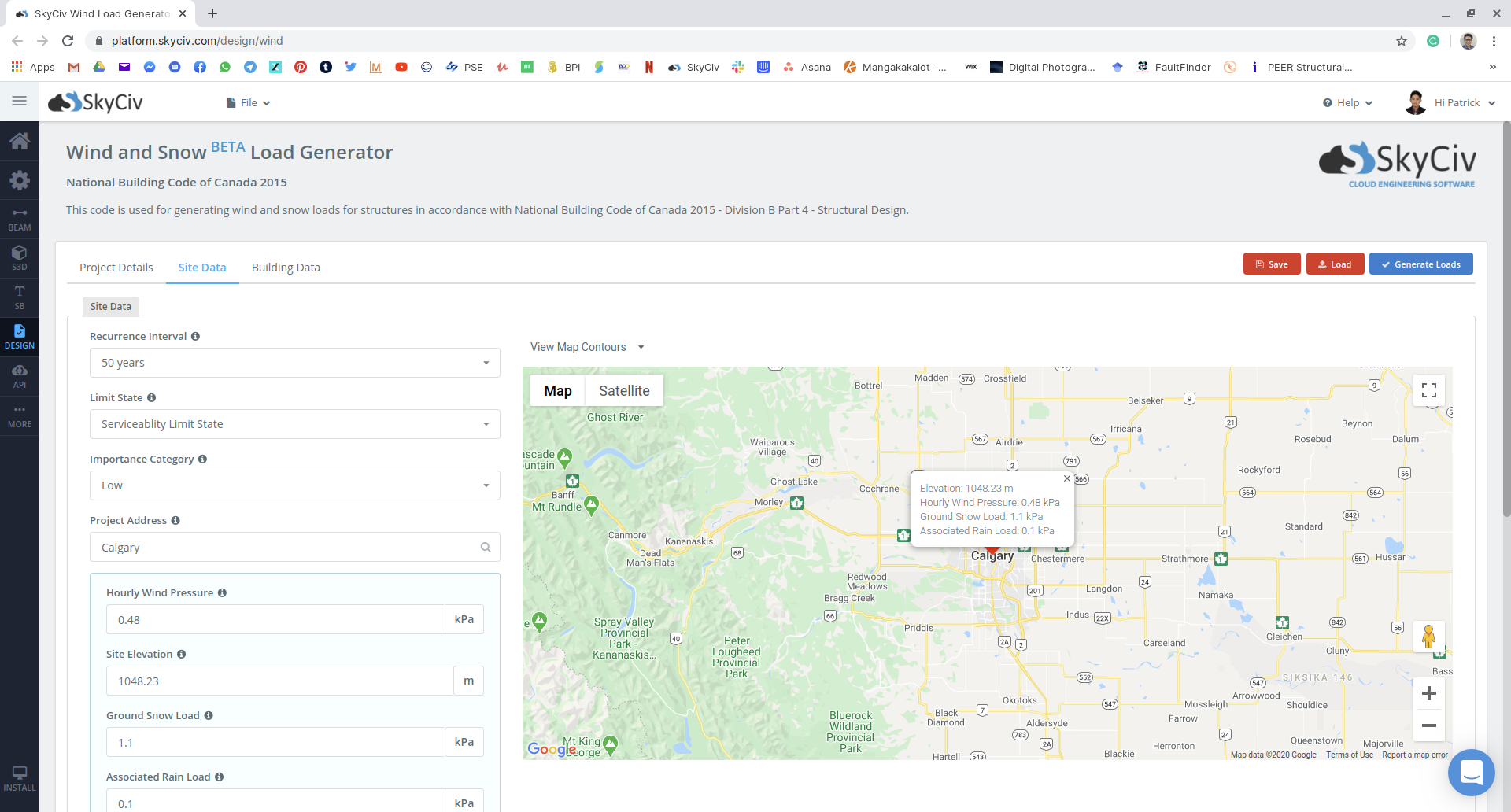
Figura 15: Entrada de dados do site no módulo SkyCiv Load Generator usando nosso exemplo.
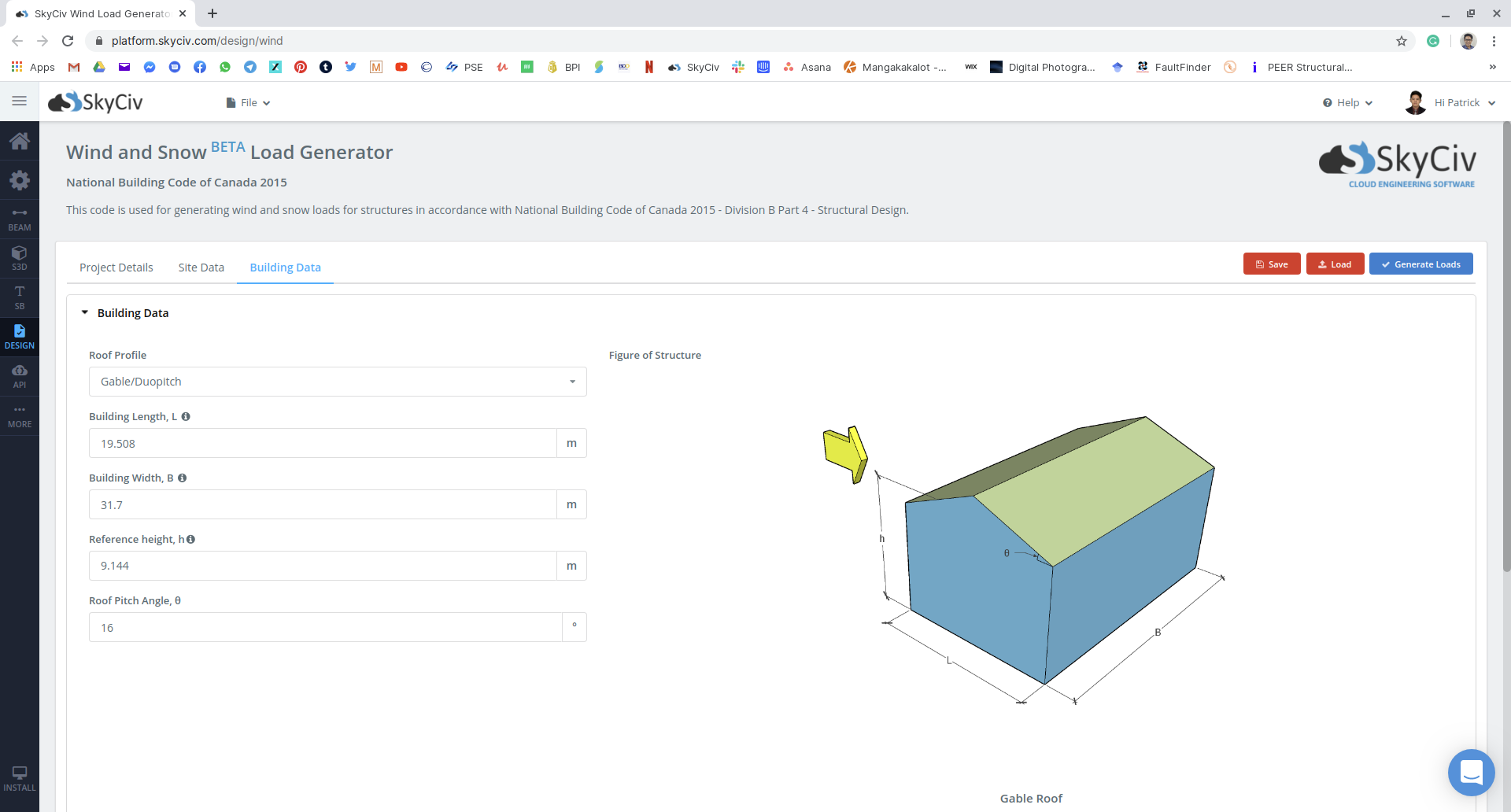
Figura 16: Entrada de parâmetro de construção e neve no módulo SkyCiv Load Generator usando nosso exemplo.
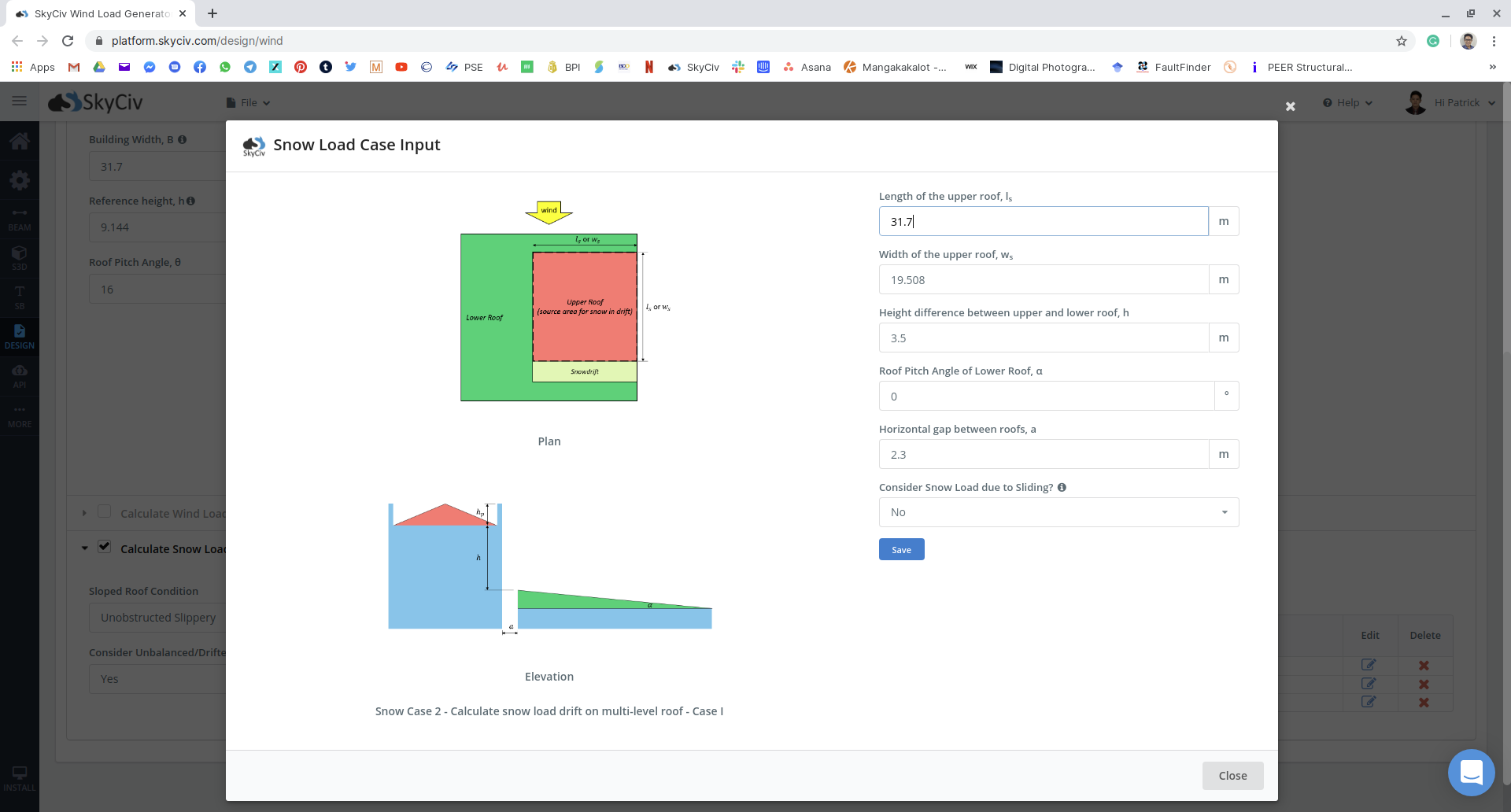
Figura 17: Entrada de carga de neve para vários casos desequilibrados para o exemplo.
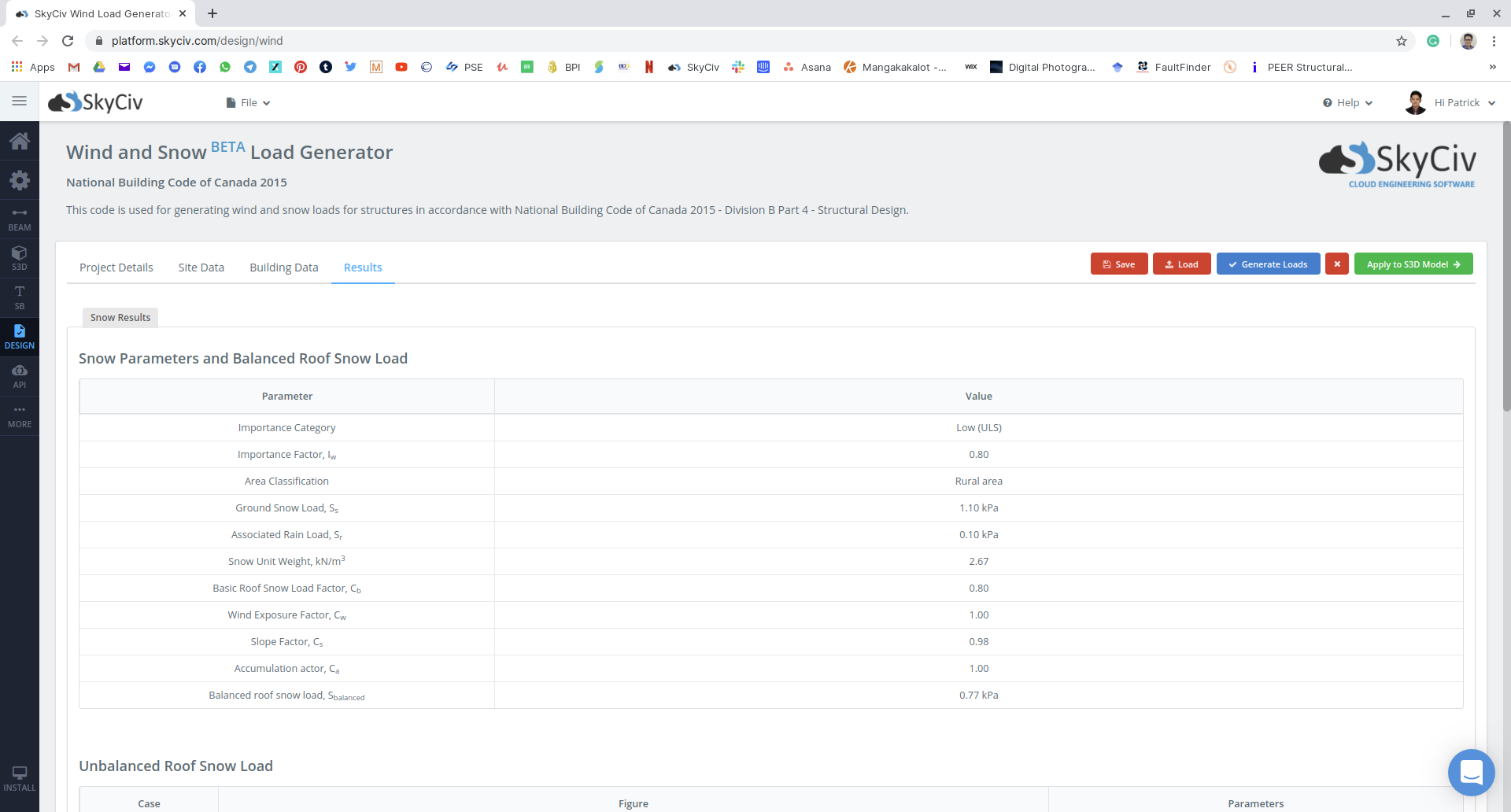
Figura 18: Resumo dos parâmetros de carga de neve usados e a carga de neve balanceada a ser aplicada à estrutura.
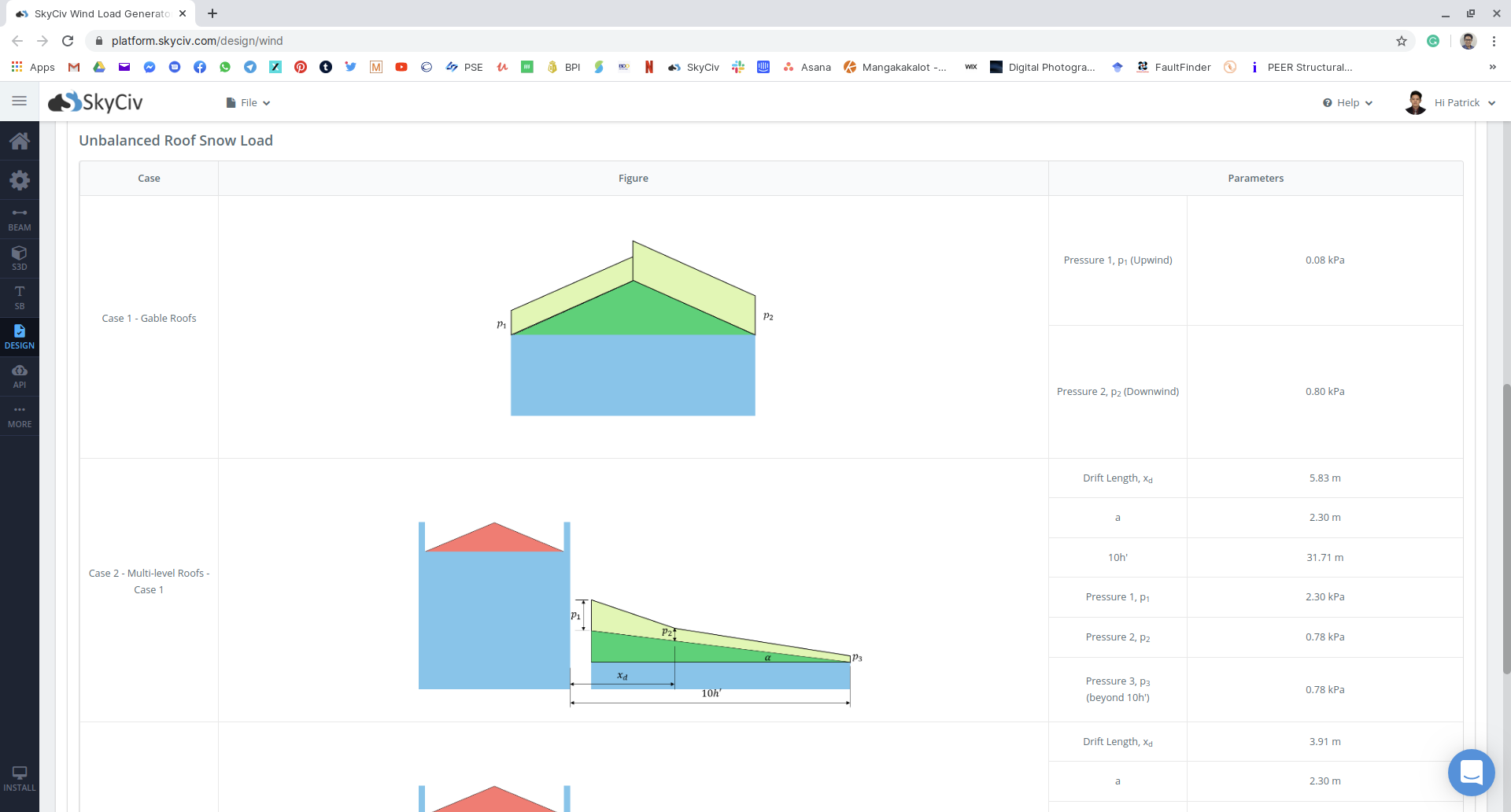
Figura 19: Resumo dos resultados de carga de neve desequilibrada.
Os cálculos de carga de neve no módulo SkyCiv Load Generator são suportados por códigos de referência como ASCE 7-10, 7-16, EN 1991-1-3, NBCC 2015, e AS / NZS 1170.3, e está disponível no Estar sozinho (Apenas gerador de carga) e Professional contas. Familiarizado com programação e APIs? Esta funcionalidade pode ser automatizada com o uso do API SkyCiv.
Engenheiro estrutural, Desenvolvimento de Produto
MS Engenharia Civil
Referências:
- Conselho Nacional de Pesquisa do Canadá. (2015). Código Nacional de Construção do Canadá, 2015. Conselho Nacional de Pesquisa do Canadá.
Observação:
- Referência do código NBCC para o “Fator básico de carga de neve no telhado” — procurar 4.1.6.2 Frase (2)
- Referência do código NBCC para o “Fator de Exposição ao Vento” — procurar 4.1.6.2 Frases (3) e (4)
- Referência do código NBCC para o “Fator de inclinação” — procurar 4.1.6.2 Frases (5), (6), e (7)
- Referência do código NBCC para o “Fator de Acumulação” — procurar 4.1.6.2 Frase (8), 4.1.6.5 para telhados de vários níveis, 4.1.6.6 para telhados com lacuna, e 4.1.6.9 para telhados de duas águas



