Um exemplo totalmente trabalhado de Eurocódigo 1 (EN 1991-1-4) cálculos de carga de vento
Neste exemplo, estaremos calculando a pressão do vento do projeto para uma estrutura de armazém localizada em Aachen, Alemanha. Nossas referências serão o Eurocódigo 1 EN 1991-1-4 Ação em estruturas (carga de vento) e DIN EN 1991-1-4 / NA:2010-12. Estaremos usando um modelo de nosso S3D para demonstrar como as cargas são aplicadas em cada superfície.
Figura 1. Modelo de armazém no SkyCiv S3D como exemplo.
Figura 2. Localização do site (do Google Maps).
Tabela 1. Dados do edifício necessários para o cálculo de vento.
| Localização | Aachen, Alemanha |
|---|---|
| Ocupação | Diversos – Estrutura do Armazém |
| Terreno | Terreno plano, agrícola |
| Dimensões | 19.507 m (d) × 31.699 m (b) no plano Eave altura de 9.144 m Apex de altura em elev. 10.973 m (h) Inclinação do telhado 3:16 (10.62°) Sem abrir |
| Revestimento | Purlins espaçados em 0.6 m Vigas de parede espaçadas em 0.6 m |
A fórmula para determinar a pressão do vento do projeto é:
Para velocidade básica do vento:
\({v}_{b} = {c}_{para você} {c}_{estação} {v}_{b,0}\) (1)
Onde:
\({v}_{b}\) = velocidade básica do vento em m / s
\({c}_{para você}\) = fator direcional
\({c}_{estação}\)= fator sazonal
\({v}_{b,0}\) = valor fundamental da velocidade básica do vento (Anexo Nacional DIN para EN 1991-1-4)
Para pressão de velocidade básica:
\({q}_{b} = 0.5 {⍴}_{ar} {{v}_{b}}^{2} \) (2)
Onde:
\({q}_{b}\) = pressão do vento projetada em Pa
\({⍴}_{ar}\) = densidade do ar (1.25 kg / cu.m.)
\({v}_{b}\)= velocidade básica do vento em m / s
Para pressão de pico:
\({q}_{p}(z) = 0.5 [1 + 7 {eu}_{v}(z)] {⍴}_{ar} {{v}_{m}(z)}^{2} \) (3)
Onde:
\({v}_{m}(z)\) = velocidade média do vento, m / s = \({c}_{r}(z) {c}_{o}(z) {v}_{b}\) (4)
\({c}_{o}(z)\) = fator de topografia
\({c}_{r}(z)\) = fator de rugosidade:
\({c}_{r}(z) = {k}_{T} em(\fratura{z}{{z}_{0}}) : {z}_{min} ≤ {z} ≤ {z}_{max}\) (5)
\({c}_{r}(z) = {c}_{r}({z}_{min}) : {z} ≤ {z}_{min}\) (6)
Onde:
\({z}_{0}\) = comprimento de rugosidade, m
\({k}_{T}\) = fator de terreno, dependendo do comprimento de rugosidade, \({z}_{0}\) calculado usando:
\({k}_{T} = 0.19 {(\fratura{{z}_{0}}{{z}_{0,II}})}^{0.07} \) : \( {z}_{0,II} = 0.05\) (categoria de terreno II) (7)
\({z}_{min}\) = altura mínima
\({z}_{max}\) = altura máxima considerada como 200 m.
A partir dessas equações (4) para (7), DIN EN 1991-1-4 / NA:2010-12 O Anexo B resume a fórmula para cada parâmetro dependendo da categoria do terreno:
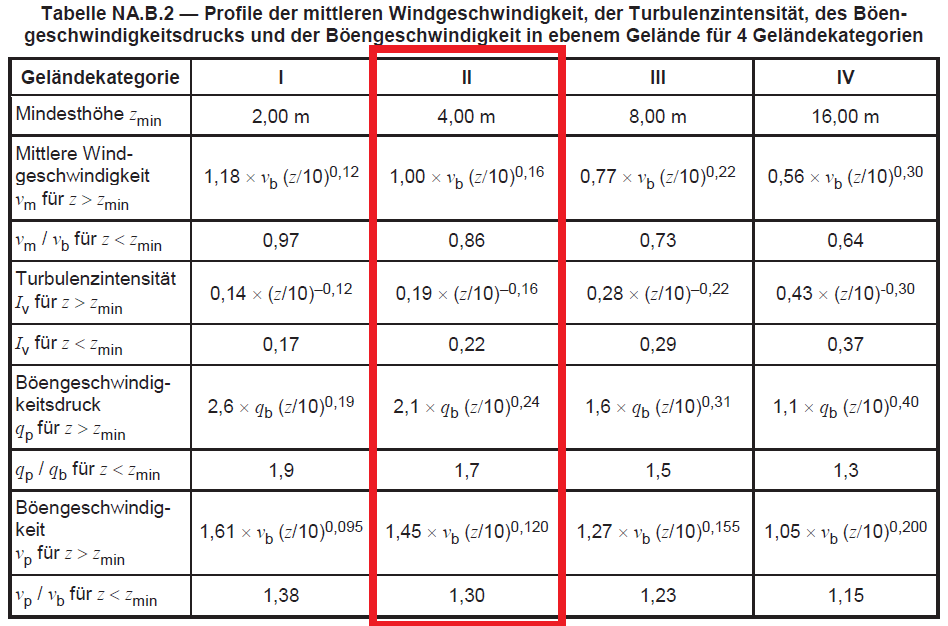
Figura 3. Tabela NA.B.2 de DIN EN 1991-1-4 / NA:2010-12.
Cada parâmetro será discutido posteriormente.
Categoria de Terreno
A estrutura está localizada em terras agrícolas, que é classificado como Categoria de Terreno II conforme definido no Anexo A de EN 1991-1-4 e Tabela NA.B-1 do Anexo Nacional DIN.
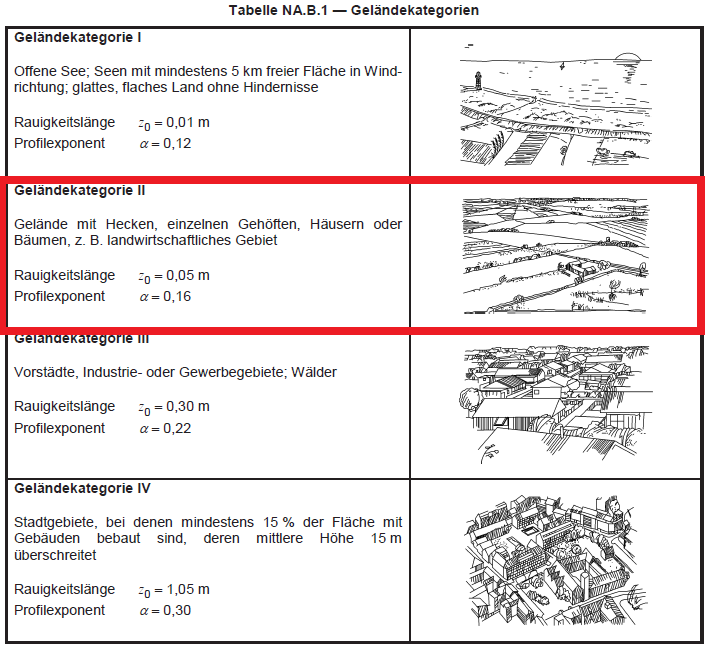
Figura 4. Tabela NA.B.1 da DIN EN 1991-1-4 / NA:2010-12.
Fatores direcionais e sazonais, \({c}_{para você}\) & \({c}_{estação}\)
A fim de calcular para a Equação (1), precisamos determinar os fatores direcionais e sazonais, \({c}_{para você}\) & \({c}_{estação}\). Anexo Nacional DIN para EN 1991-1-4 simplifica este cálculo, pois os valores sugeridos desses fatores são iguais a 1.0.
Velocidade e pressão básicas do vento, \({v}_{b,0}\) & \({q}_{b,0}\)
Como mencionado anteriormente, o mapa de velocidade do vento para a Alemanha pode ser obtido no DIN National Annex para EN 1991-1-4. Cada país europeu tem um anexo nacional separado no qual calibra os parâmetros de carga do vento sugeridos de EN 1991-1-4.
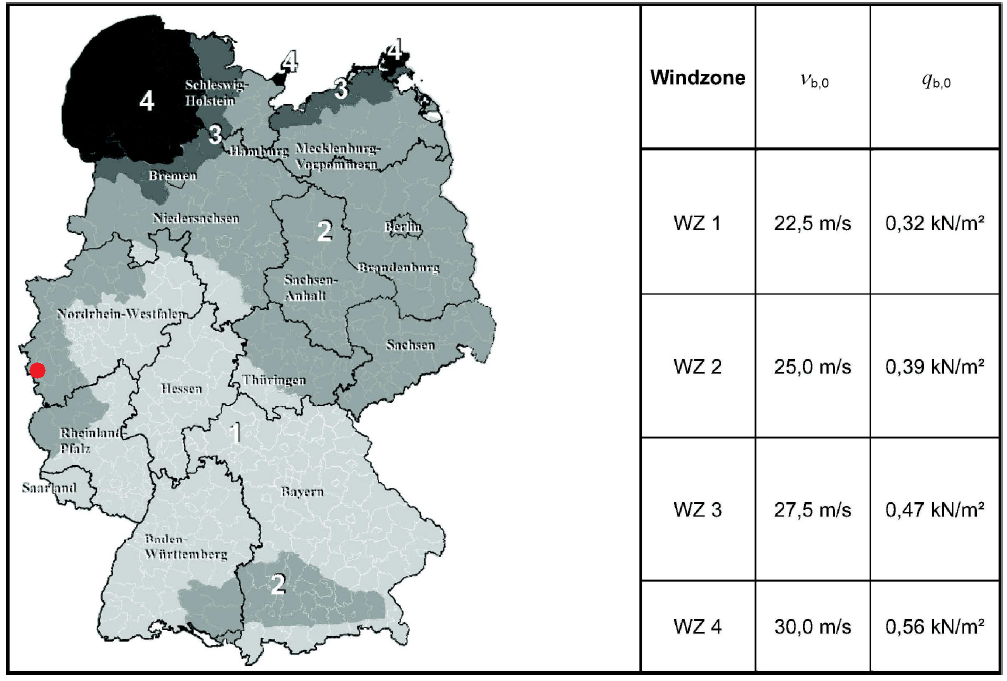
Figura 5. Tabela NA.A.1 da DIN EN 1991-1-4 / NA:2010-12.
Para a localização do nosso site, Aachen, A Alemanha está localizada em WZ2 com \({v}_{b,0}\) = 25.0 em como mostrado na figura acima. Deste valor, optimizada \({c}_{para você}\) & \({c}_{estação}\) são ambos iguais a 1.0, podemos calcular a pressão básica do vento, \({q}_{b,0}\), usando equações (1) e (2). Conseqüentemente, o valor correspondente de \({q}_{b,0}\) = 0.39 kPa , também indicado no mapa de vento do Anexo Nacional DIN para EN 1991-1-4.
SkyCiv agora automatiza a detecção da região do vento e obtém o valor da velocidade do vento correspondente com apenas algumas entradas. Tentar nosso SkyCiv Free Wind Tool
Velocidade média do vento, \({v}_{m}(z)\)
Para calcular a pressão de pico, \({q}_{p}(z)\), precisamos determinar o valor da velocidade média do vento, \({v}_{m}(z) \). Da Figura 3, podemos calcular a velocidade média, \({v}_{m}(z) \):
Pra \({z}_{min} ≤ {z} ≤ {z}_{max} : 1.0 {v}_{b} {(0.1z)}^{0.16} \)
Pra \({z}_{min} ≤ {z} ≤ {z}_{max} : 0.86 {v}_{b} \)
Pressão de pico, \({q}_{p}(z)\)
similarmente, o pico de pressão, \({q}_{p}(z)\), pode ser resolvido usando a Figura 3:
Pra \({z}_{min} ≤ {z} ≤ {z}_{max} : 2.1 {q}_{b} {(0.1z)}^{0.24} \)
Pra \({z} ≤ {z}_{min} : 1.7 {q}_{b} \)
Para calcular a pressão de pico, \({q}_{p}(z) \), precisamos determinar o valor da velocidade média do vento, \({v}_{m}(z) \). Da Figura 3, podemos calcular a velocidade média, \({v}_{m}(z) \):
pra \({z}_{min} ≤ {z} ≤ {z}_{max} : 1.0 {v}_{b} {(0.1z)}^{0.16} \)
pra \({z} ≤ {z}_{min} : 0.86 {v}_{b} \)
Os resultados para a velocidade média do vento e pressão de pico para cada nível são mostrados na Tabela 2 abaixo.
Tabela 2. Velocidade média do vento calculada e pressão de pico para cada nível da estrutura.
| altura / nível | \({v}_{m}(z)\), em | \({q}_{p}(z)\), Nós vamos |
|---|---|---|
| 3.00 | 21.5 | 664.06 |
| 6.00 | 23.04 | 725.66 |
| 9.00 | 24.58 | 799.83 |
| 10.97 (h) | 25.37 | 838.80 |
Pressão Externa do Vento, \({C}_{e}\)
Após o cálculo da pressão de pico, \({q}_{p}(z)\), a pressão do vento externa atuando na superfície da estrutura pode ser resolvida usando:
\({C}_{e} = {q}_{p}(z) {c}_{sobre}\) (8)
Onde:
\({C}_{e}\) = pressão externa do vento, Nós vamos
\({q}_{p}(z)\) = pressão de pico, Nós vamos
\({c}_{sobre}\) = coeficiente de pressão para superfície externa
uma) Paredes Verticais
Para distribuição de pressão de barlavento (Zona D), Seção 7.2.2 ou e 1991-1-4 descreve como deve ser distribuído dependendo de \(h ), \(b\), e \(d\). Para nosso exemplo, temos \(h < b\) (10.973 < 31.699m), por isso, \({z}_{e} = h\) como mostrado na figura 6.
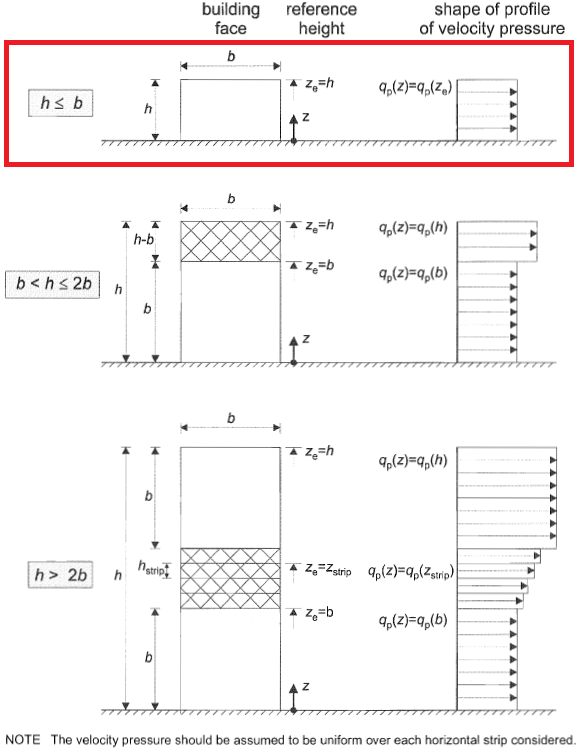
Figura 6. Distribuição de pressão para a parede de barlavento com base na Figura 7.4 ou e 1991-1-4.
Por outro lado, distribuição de pressão para paredes laterais (Zonas A a C) são mostrados na Figura 7.5 ou e 1991-1-4 e depende do \(e = b < 2h ). Para nosso exemplo, o valor de \(e = 21.946\), por isso, \(e > d\) como mostrado na figura 7. Além disso, a pressão da parede de sotavento é designada como Zona E. Os coeficientes de pressão externa são então indicados na Figura 8 com base na Tabela NA.1 da DIN EN 1991-1-4 / NA:2010-12.
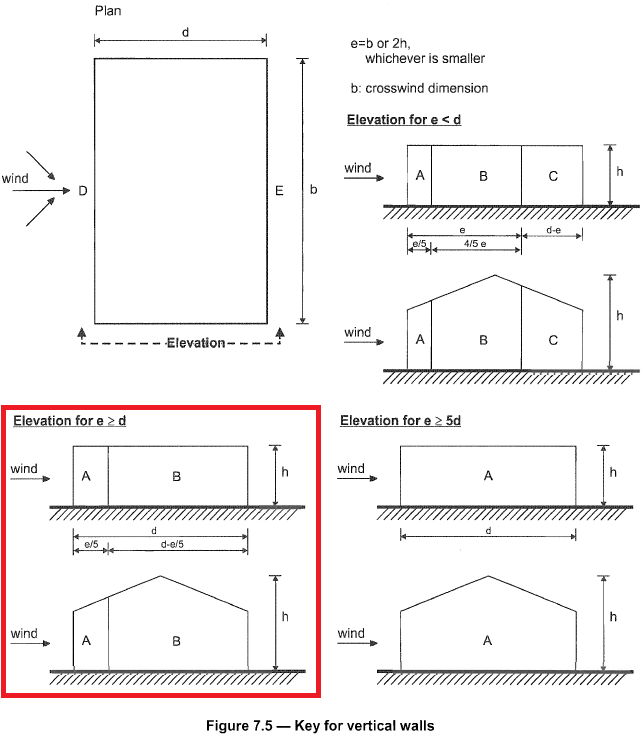
Figura 7. Distribuição de pressão para parede lateral com base na Figura 7.5 ou e 1991-1-4.
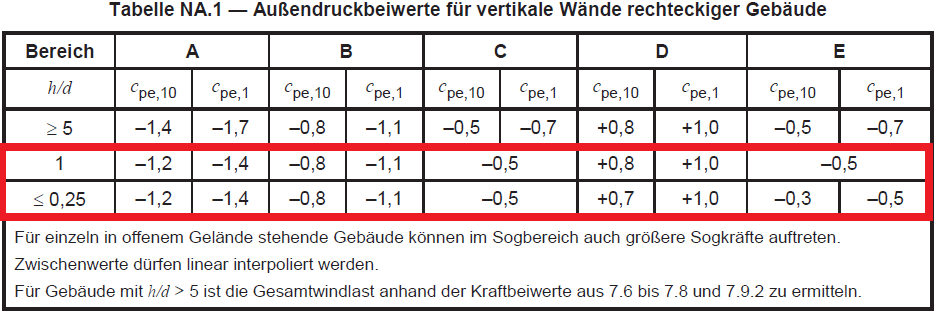
Figura 8. Coeficiente de pressão externa para paredes verticais (Zonas A a E) com base na Tabela NA.1 da DIN EN 1991-1-4 / NA:2010-12.
Desde a \(h / d = 0.563\), precisaremos interpolar o \({c}_{sobre}\) valores a fim de calcular para a pressão do vento projetada. Os subscritos para \({c}_{sobre,10}\) e \({c}_{sobre,1}\) significa que o valor depende da área onde a pressão do vento é aplicada, para qualquer 1 m2. e 10 m2. Geralmente, para edifícios, \({c}_{sobre,10}\) é aquele a ser adotado desde \({c}_{sobre,1}\) é usado para pequenos elementos, como revestimentos e elementos de cobertura. Os valores interpolados para \({c}_{sobre}\) são mostrados na Tabela 3 abaixo.
Tabela 3. Coeficiente de pressão externa calculado para paredes verticais.
| \(h / d ) | A | B | C | D | E |
|---|---|---|---|---|---|
| 1.000 | -1.2 | -0.8 | -0.5 | 0.8 | -0.5 |
| 0.563 | -1.2 | -0.8 | -0.5 | 0.742 | -0.383 |
| 0.250 | -1.2 | -0.8 | -0.5 | 0.7 | -0.3 |
b) Cobertura
A distribuição das pressões do vento do projeto para o telhado são detalhadas nas seções 7.2.3 para 7.2.10 e 7.3 ou e 1991-1-4. Especificamente, uma vez que o perfil do telhado de nossa estrutura é duopitch, estaremos usando Section 7.2.5 para obter os coeficientes de pressão externa do telhado, \({c}_{sobre}\), como mostrado na figura 9 e 10 abaixo.
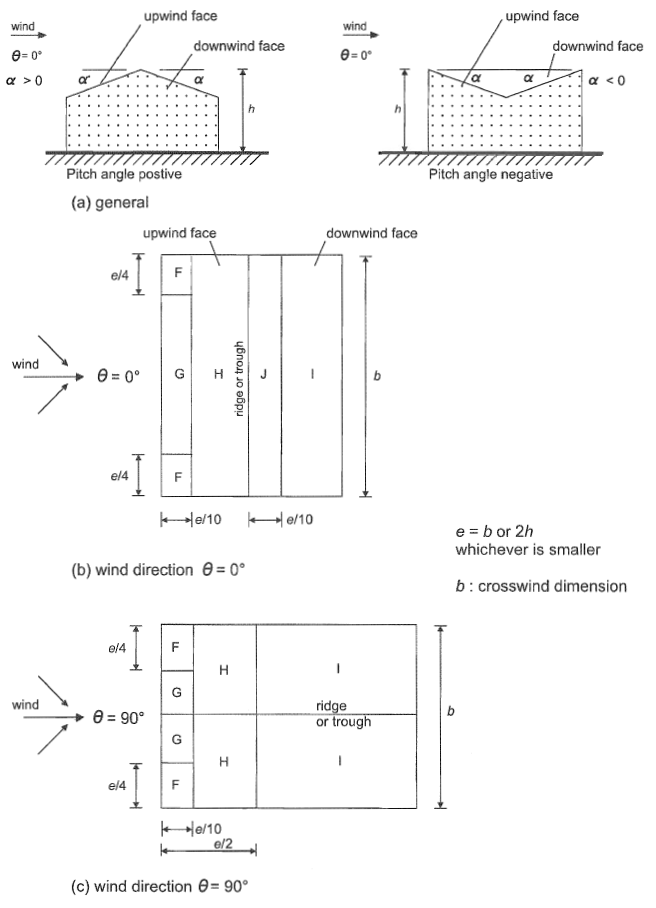
Figura 9. Distribuição de pressão para telhado duopitch com base na Figura 7.8 ou e 1991-1-4.
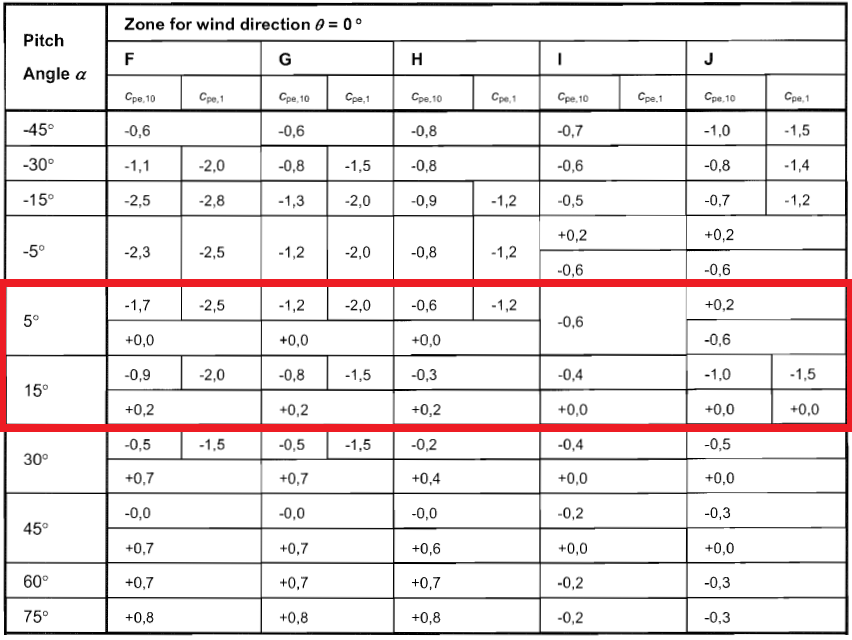
Figura 9. Coeficiente de pressão externa para paredes de superfícies de telhado (Zonas F a J) com base na Tabela 7.4a de EN 1991-1-4.
Uma vez que o ângulo de inclinação do telhado é igual a 10,62 °, precisamos interpolar o \({c}_{sobre}\) valores de 5 ° e 15 °. Conseqüentemente, o calculado \({c}_{sobre}\) valores para a nossa estrutura são mostrados na Tabela 4 abaixo.
Tabela 4. Coeficiente de pressão externa calculado para superfícies de telhado.
| \(h / d ) | Zona F | Zona G | Zona H | Zona I | Zona J | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(-{c}_{a}\) | \(+{c}_{a}\) | \(-{c}_{a}\) | \(+{c}_{a}\) | \(-{c}_{a}\) | \(+{c}_{a}\) | \(-{c}_{a}\) | \(+{c}_{a}\) | \(-{c}_{a}\) | \(+{c}_{a}\) | |
| 5.00 | -1.7 | 0.0 | -1.2 | 0.0 | -0.6 | 0.0 | -0.6 | – | -0.6 | 0.2 |
| 10.62 | -1.250 | 0.112 | -0.975 | 0.112 | -0.431 | 0.112 | -0.488 | – | -0.825 | 0.088 |
| 15.00 | -0.9 | 0.2 | -0.8 | 0.2 | -0.3 | 0.2 | -0.4 | – | -1.0 | 0.0 |
Pressão Interna do Vento, \({C}_{I}\)
Pressão interna do vento, \({C}_{I}\), pode desenvolver e vai atuar simultaneamente com a pressão do vento externa. Conseqüentemente, a necessidade de calcular \({C}_{I}\) é necessário. A fórmula para calcular \({C}_{I}\) é:
\({C}_{I} = {q}_{p}(z) {c}_{pi}\) (9)
Onde:
\({C}_{I}\) = pressão interna do vento, Nós vamos
\({q}_{p}(z)\) = pressão de pico, Nós vamos
\({c}_{pi}\) = coeficiente de pressão interna
Seção 7.2.9 ou e 1991-1-4 afirma que \({c}_{pi}\) pode ser considerado o mais oneroso de +0.2 e -0.3. Assumimos que nossa estrutura não tem abertura dominante.
Projetar a pressão do vento
Com estas \({c}_{sobre}\) e \({c}_{pi}\) valores, agora podemos calcular a pressão do vento externo correspondente para cada zona, conforme mostrado na Tabela 5.
Tabela 5. Calculou a pressão do vento externo em cada superfície.
| Superfície | Zona | \({C}_{e}\) | \({C}_{I}\) | Combinado \({C}_{e}\) e \({C}_{I}\) | |||
|---|---|---|---|---|---|---|---|
| \(-{c}_{sobre}\) | \(+{c}_{sobre}\) | \(+{c}_{pi}\) | \(+{c}_{pi}\) | valor mínimo | Valor máximo | ||
| muro | Zona A | -1006.56 | 167.76 | -251.64 | -1174.32 | 754.92 | |
| Zona B | -671.04 | – | -838.80 | -419.40 | |||
| Zona C | -419.40 | – | -587.16 | 167.76 | |||
| Zona D | – | 622.11 | 454.35 | 873.75 | |||
| Zona E | -321.54 | – | -489.30 | -69.9 | |||
| Cobertura | Zona F | -1048.83 | 94.28 | -1216.59 | 345.92 | ||
| Zona G | -818.00 | 94.28 | -985.76 | 345.92 | |||
| Zona H | -361.86 | 94.28 | -529.62 | 345.92 | |||
| Zona I | -409.00 | -576.76 | -157.36 | ||||
| Zona J | -691.84 | 73.48 | -859.60 | 325.12 | |||
A partir desses valores, podemos agora aplicar essas pressões do vento de projeto à nossa estrutura. Considerando uma baia de quadro (interno), o combinado \({C}_{e}\) e \({C}_{I}\) é o seguinte:
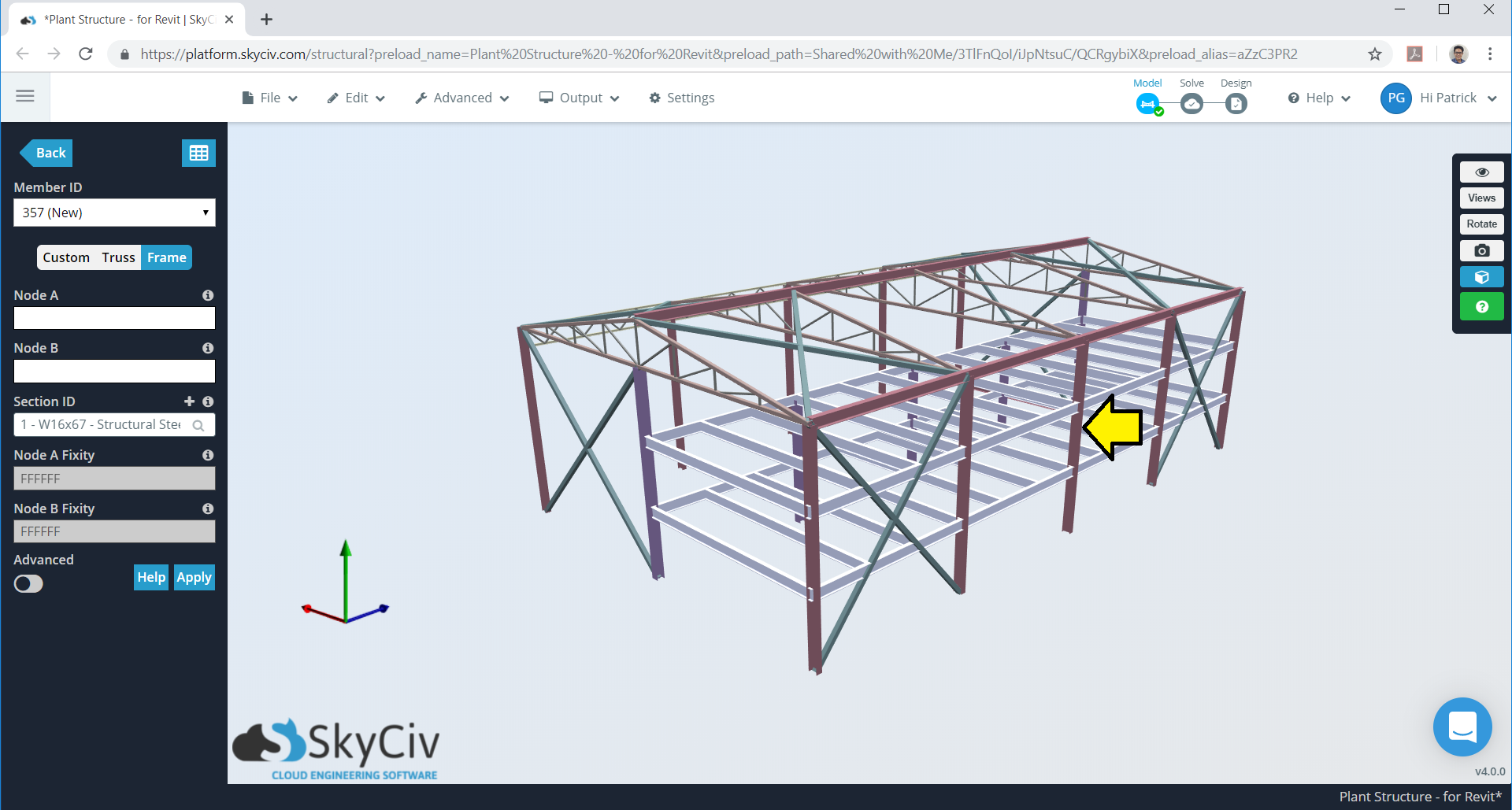
Figura 10. Quadro interno a ser considerado.
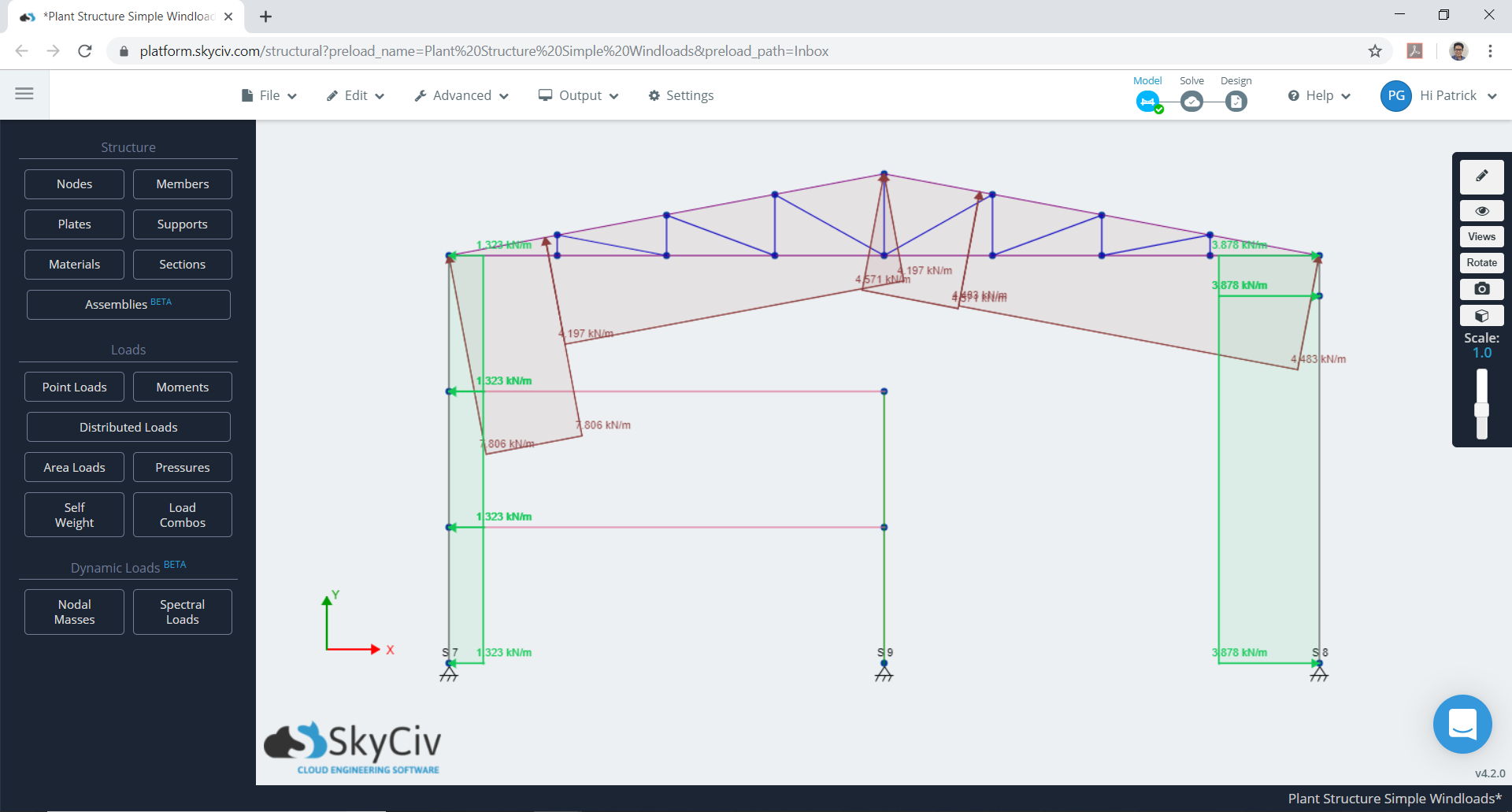
Figura 11. Caso mínimo para combinado \({C}_{e}\) e \({C}_{I}\).
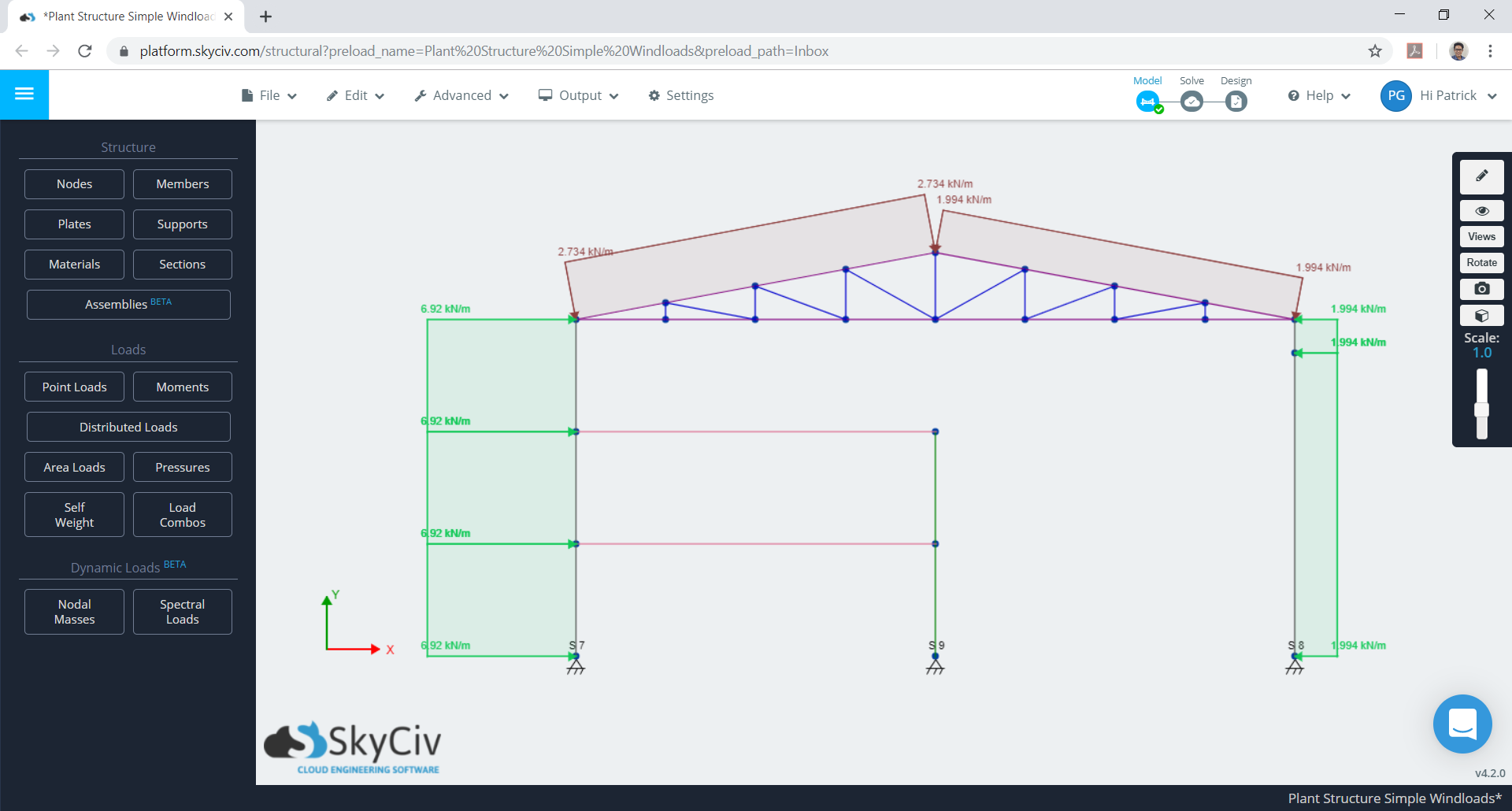
Figura 12. Caso máximo para combinado \({C}_{e}\) e \({C}_{I}\).
Todos esses cálculos podem ser realizados usando o Software de carregamento de vento da SkyCiv para ASCE 7-10, 7-16, EN 1991, NBBC 2015 e a norma AS 1170. Os usuários podem inserir a localização do local para obter as velocidades do vento e os fatores topográficos, além de inserir os parâmetros do edifício e gerar as pressões de vento. Com uma conta profissional, os usuários podem aplicar isso automaticamente a um modelo estrutural e executar análises estruturais em um único software.
Caso contrário, tentar nosso SkyCiv Free Wind Tool para cálculos de velocidade e pressão do vento em estruturas simples.
Engenheiro estrutural, Desenvolvimento de Produto
MS Engenharia Civil
Referências:
- Sobre, B. (2005). Eurocódigo 1: Ações em Estruturas - Parte 1-4: Ações Gerais - Ações do Vento.
- DIN EN 1991-1-4. (2005). Eurocódigo 1: Ações em estruturas Parte 1-4: Ações gerais, Windlasten; Versão alemã EN 1991-1-4: 2005.



