Este artigo discute dois exemplos de projeto de laje de concreto armado, incluindo dobra unidirecional e bidirecional. O objetivo principal é comparar os resultados obtidos entre os cálculos manuais e o Módulo de Design de Placas SkyCiv. Usaremos o Eurocódigo 2 para Estruturas de Concreto Armado.

Os códigos de construção têm abordagens semelhantes ao definir os casos típicos de lajes. Se você quiser aprender um pouco mais sobre este assunto, sugerimos que você leia os seguintes artigos sobre design de lajes Exemplo de projeto de laje ACI e comparação com SkyCiv e Exemplo de projeto de laje AS3600 de padrões australianos e comparação com SkyCiv

Exemplo de projeto de laje unidirecional

O primeiro caso a analisar é um pequeno edifício de um piso (Figura 1, Figura 2) que tem um comportamento de laje descrito como em uma direção.

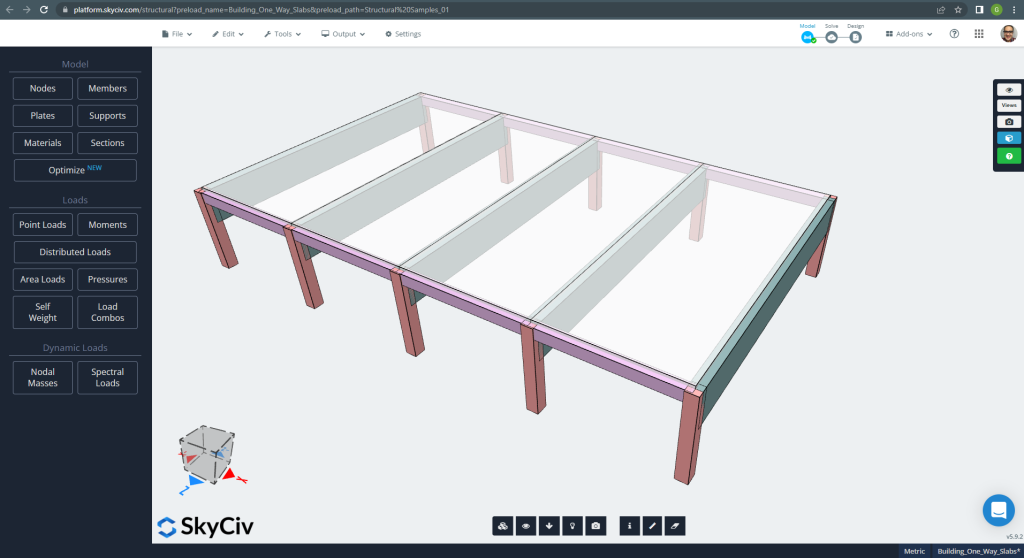
Figura 1. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

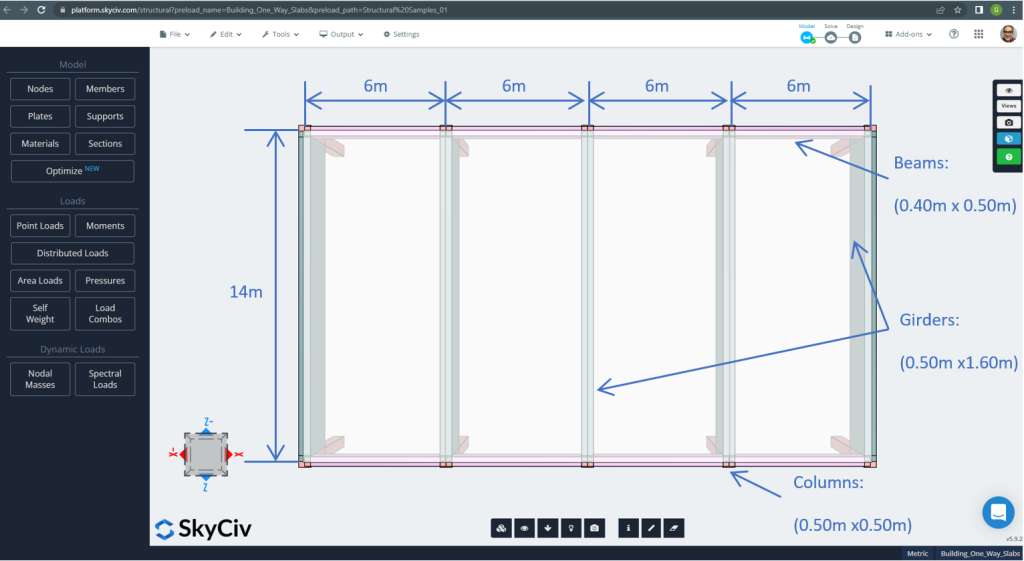
Figura 2. Exemplo de lajes unidirecionais em um pequeno edifício (dimensões do plano). (3D estrutural, Engenharia de Nuvem SkyCiv).

Para o exemplo de laje, resumindo, o material, propriedades dos elementos, e cargas a considerar :

• Classificação do tipo de laje: Um – comportamento de maneira \(\fratura{L_2}{L_1} > 2 ; \fratura{14m}{6m}=2,33 > 2.00 \) OK!
• ocupação do edifício: Uso residencial
• Espessura da laje \(t_{laje}=0.25m\)
• Densidade do concreto armado \(\rho_w = 25 \fratura{kN}{m^3}\)
• Resistência à compressão característica do concreto em 28 dias (C25\30) \(fck = 25 MPa \)
• Peso próprio da laje \(Dead = \rho_w \times t_{laje} = 25 \fratura{kN}{m^3} \vezes 0,25m = 6.25 \fratura {kN}{m^2}\)
• Carga morta superimposta \(SD = 3.0 \fratura {kN}{m^2}\)
• Carga viva \(L = 2.0 \fratura {kN}{m^2}\)

Cálculos manuais de acordo com EN-2

Nesta secção, calcularemos o vergalhão de aço reforçado necessário usando a referência do padrão do Eurocódigo. Primeiro obtemos o momento fletor fatorado total a ser realizado pela faixa de largura unitária da laje.

• Carga morta, \(g = (3.0 + 6.25) \fratura{kN}{m^2} \vezes 1 m = 9.25 \fratura{kN}{m}\)
• Carga viva, \(q = (2.0) \fratura{kN}{m^2} \vezes 1 m = 2.0 \fratura{kN}{m}\)
• carga final, \(Fd = 1.35\times g + 1.5\vezes q = (1.35\vezes 9.25 + 1.5\vezes 2.0)\fratura{kN}{m} =15.5 \frac{kN}{m} \)

Antes de obter a área de reforço de aço, temos que verificar as relações de profundidade efetiva do vão. Dois casos principais:

Sistema Estrutural		Relação básica de profundidade efetiva do vão
	Fator para sistema estrutural K	Concreto altamente estressado %(\(\ro = 1.5 )\)	Concreto levemente estressado %(\(\ro = 0.5 )\)
1. Vão final de viga contínua ou laje contínua unidirecional ou laje bidirecional contínua em um dos lados	1.3	18	26
2. Vão interior de vigas contínuas ou lajes armadas de uma ou duas vias	1.5	20	30

O caso mais crítico é para o número um, então, selecionamos uma proporção de 26.

• \(t_{min}= frac{L}{EU SEI}+cover+0.5\dot bar_{diâmetro}= frac{6m}{26}+0.025m+0.5\times 12mm=0.26m \) ~ \(0.25m ). A espessura total ainda é adequada, OK!

Agora, é hora de usar a mesa para lajes contínuas unidirecionais:

	Condição de suporte final				No primeiro apoio interior	A meio de vãos interiores	Em suportes internos
	Articulado		Contínuo
	Suporte externo	Perto do meio do vão final	Suporte final	Vão final
Momento	0	0.086FL	–	0.075FL	–	0.063FL	–
			0.04FL		0.086FL		0.063FL
Cisalhamento	0.4F	–		–		–
			0.46F		0.6F		0.5F

Onde:

• L é o vão efetivo
• F é a carga final total no vão (1.35Gk + 1.5Qk; Gk é a carga morta e Qk a carga viva, respectivamente)

Será explicado apenas um caso (suporte final contínuo) e o restante aparecerá na tabela a seguir.

• \(F=Fd\times L = 15.5 \fratura{kN}{m} \vezes 6m = 93.0 kN \)
• \(M=0.04FL=0.04 \times 93.0 kN \times 6m= -22.32{kN}{m}\)
• \(d = 230 mm \)
• \(K=\frac{M}{{b}{d^2}{f_{inclui cálculos detalhados passo a passo}}}= frac{22.32\vezes 10^6 {N}{milímetros}}{{1000milímetros}\vezes{(230 milímetros)^ 2}\vezes {25 \fratura{N}{mm^2}}}=0.016877\)
• \(l_a = 0.95 \)
• \(z=l_a \times d = 0.95\times 230mm = 218.50 mm\)
• \(A_s = frac{M}{{0.87}{f_{sim}}{z}}= frac{22.32\vezes 10^6 {N}{milímetros}}{0.87\vezes 500 {N}{mm^2} \vezes {218.50milímetros} = 234.83 mm^2 }\)
• \(UMA_{s,min}=0,0013{b}{d}=0.0013\times 1000mm \times 230 mm =299 mm^2\)
• \(UMA_{st}=max(Como, UMA_{s,min}) = máximo(234.83, 299) mm^2 = 299 mm^2 \)

Momentos	Exterior Negativo Esquerda	Exterior Positivo	Direita Negativa Externa	Interior Negativo Esquerda	Interior Positivo	Direito Negativo Interior
valor M, kN-m	22.32	35.15	41.85	48.00	35.15	35.15
K	0.0168	0.0266	0.03164	0.0362	0.0266	0.0266
z, milímetros	218.50	218.50	218.50	218.50	218.50	218.50
\(Como, mm^2\)	234.83	369.815	440.31	505.011	369.815	369.815
\(UMA_{s,min},mm^2\)	299.00	299.00	299.00	299.00	299.00	299.00
\(UMA_{st} {mm^2}\)	299.00	369.815	440.31	505.011	369.815	369.815

O próximo passo é calcular o aço do vergalhão de reforço usando o Plate Design Module no SkyCiv. Por favor, continue lendo a próxima seção!.

Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!

Inscreva-se no SkyCiv!

Resultados do Módulo de Projeto de Placa SkyCiv S3D

Esta seção trata da obtenção da área de reforço de aço, mas apenas usando o software, a Módulo de Design de Placa. De forma concisa, mostraremos apenas os resultados ou informações importantes através de imagens.

Antes de analisar o modelo, devemos definir um tamanho de malha de placa. Algumas referências (2) recomendar um tamanho para o elemento shell de 1/6 do curto espaço ou 1/8 do longo vão, o mais curto deles. Seguindo este valor, temos \(\fratura{L2}{6}= frac{6m}{6} = 1 m \) ou \(\fratura{L1}{8}= frac{14m}{8}=1,75m \); tomamos 1m como tamanho máximo recomendado e 0,50m de tamanho de malha aplicado.

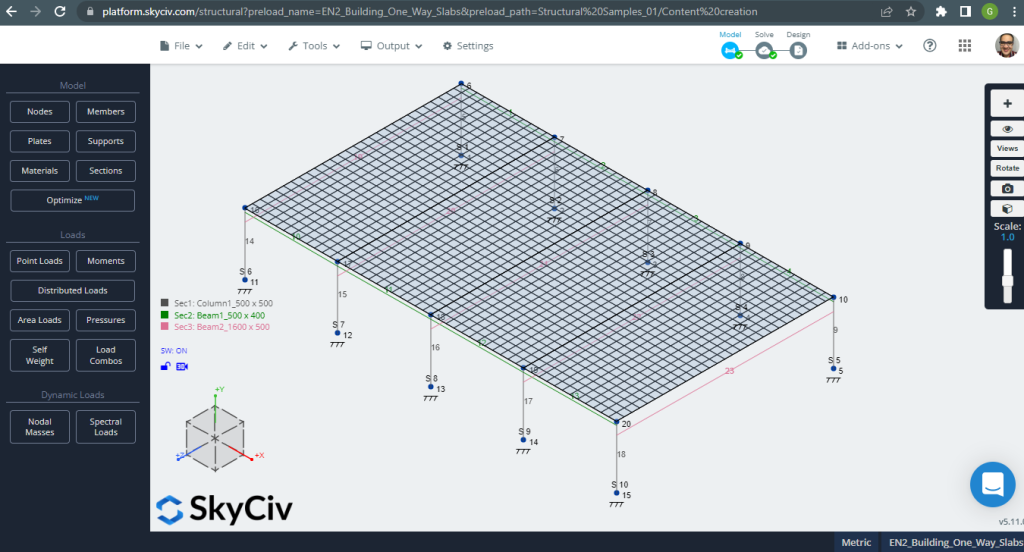
Figura 3. Placa malhada. (3D estrutural, Engenharia de Nuvem SkyCiv).

Uma vez que melhoramos nosso modelo estrutural analítico, executamos uma análise elástica linear. Ao projetar lajes, temos que verificar se os deslocamentos verticais são menores que o máximo permitido pelo código. Eurocódigo 2 estabeleceu um deslocamento vertical máximo de manutenção de \(\fratura{L}{250}= frac{6000milímetros}{250}=24.0 mm\).

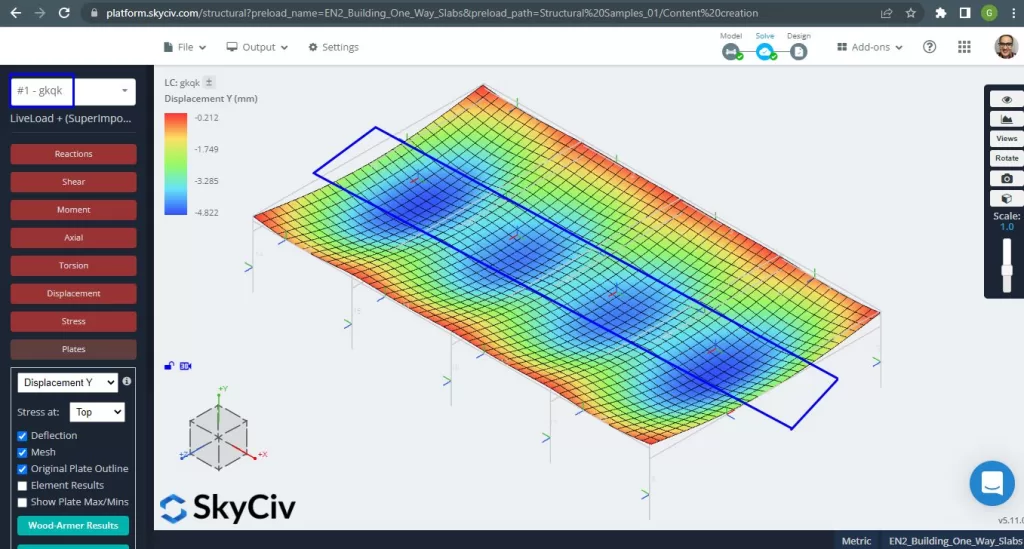
Figura 4. Deslocamento vertical, valores máximos no centro dos vãos. (3D estrutural, Engenharia de Nuvem SkyCiv).

Comparando o deslocamento vertical máximo com o valor referenciado pelo código, a rigidez da laje é adequada. \(4.822 milímetros < 24.00mm\).

Os momentos máximos nos vãos da laje situam-se para positivo no centro e para negativo nos apoios exteriores e interiores. Vamos ver os valores desses momentos nas imagens a seguir.

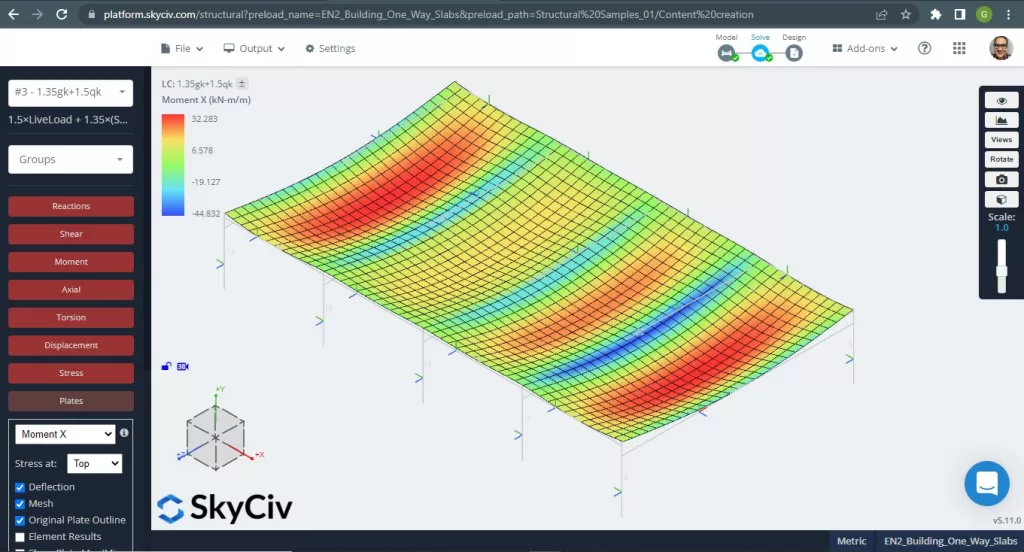
Figura 5. Momentos fletores na direção X. (3D estrutural, Engenharia de Nuvem SkyCiv).

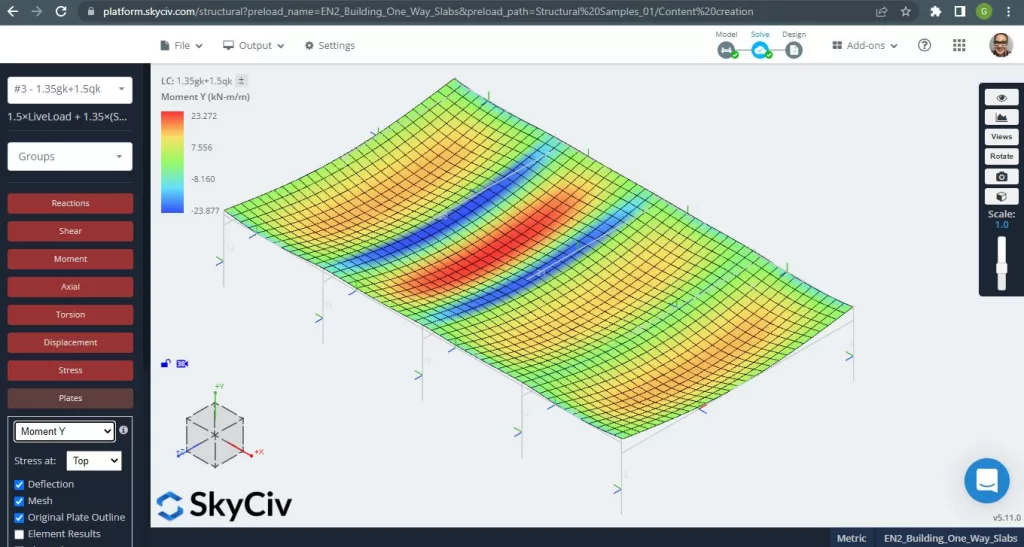
Figura 6. Momentos fletores na direção Y. (3D estrutural, Engenharia de Nuvem SkyCiv).

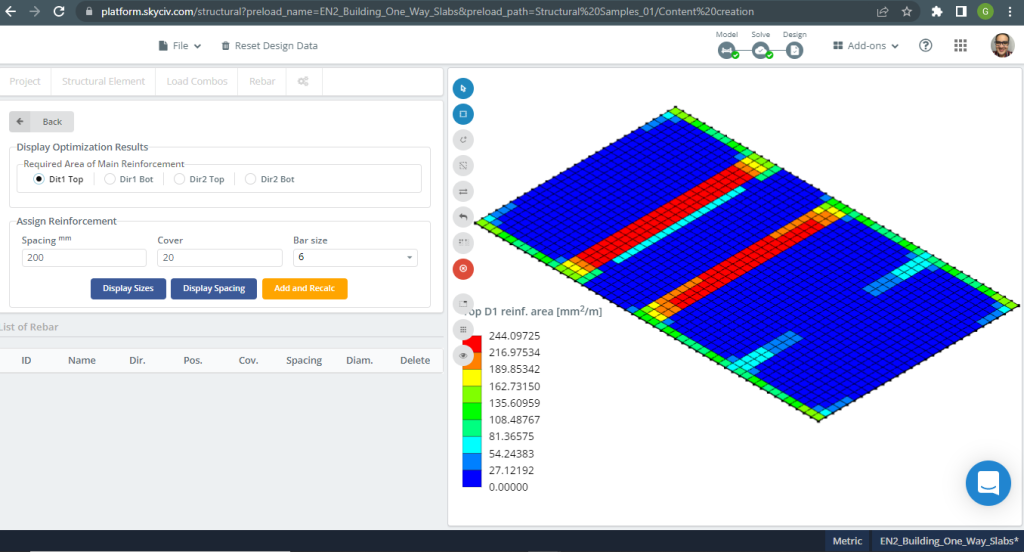
Figura 7. Reforço de aço para a direção X no topo. (3D estrutural, Engenharia de Nuvem SkyCiv).

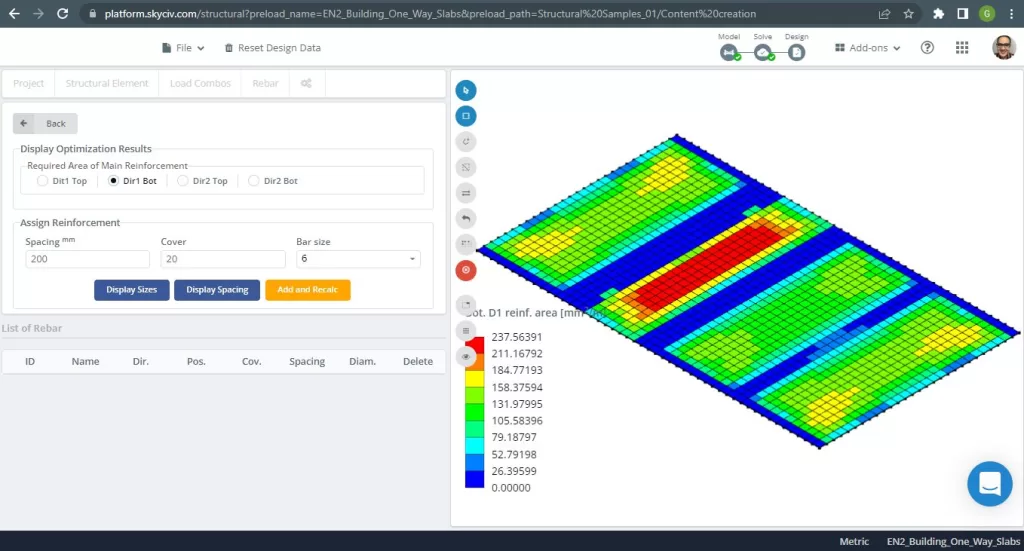
Figura 8. Reforço de aço para a direção X na parte inferior. (3D estrutural, Engenharia de Nuvem SkyCiv).

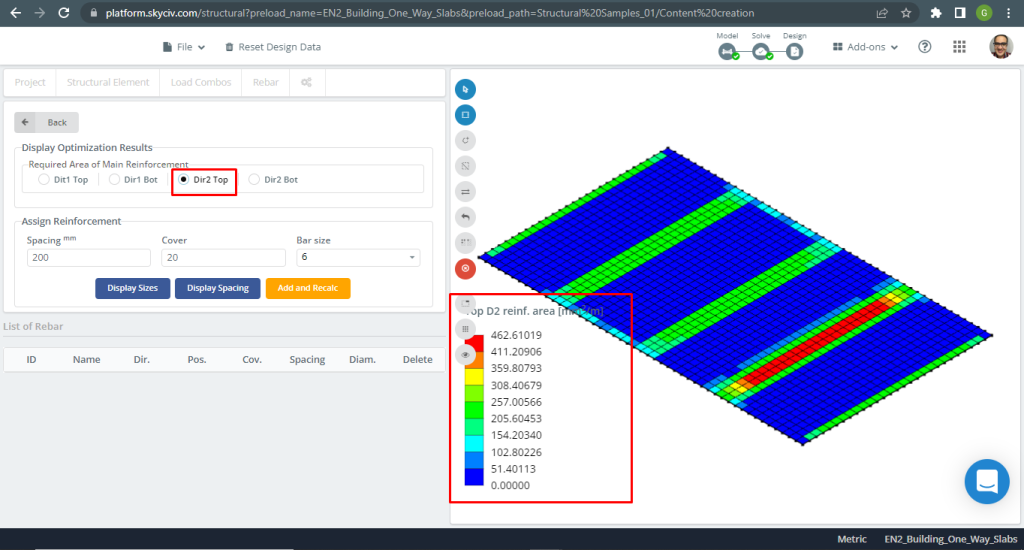
Figura 9. Reforço de aço para a direção Y no topo. (3D estrutural, Engenharia de Nuvem SkyCiv).

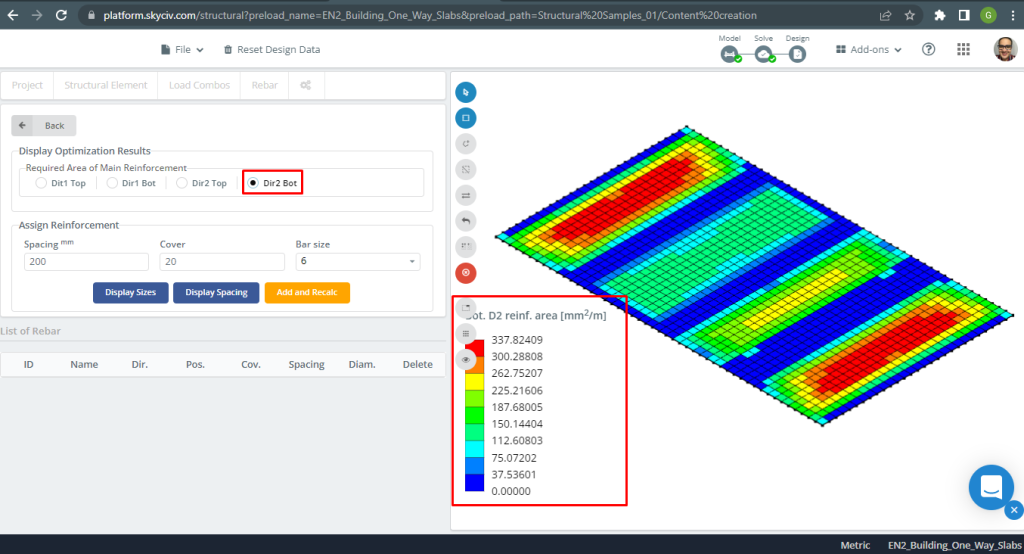
Figura 10. Reforço de aço para a direção Y na parte inferior. (3D estrutural, Engenharia de Nuvem SkyCiv).

Comparação de resultados

A última etapa neste exemplo de projeto de laje unidirecional é comparar a área do vergalhão de aço obtida pela análise S3D (eixos locais “2”) e cálculos manuais.

Momentos e área de aço	Exterior Negativo Esquerda	Exterior Positivo	Direita Negativa Externa	Interior Negativo Esquerda	Interior Positivo	Direito Negativo Interior
\(UMA_{st, HandCalcs} {mm^2}\)	299.00	369.82	440.31	505.011	369.82	369.82
\(UMA_{st, S3D} {mm^2}\)	308.41	337.82	462.61	462.61	262.75	308.41
\(\Delta_{diferente}\) (%)	3.051	8.653	4.820	8.400	28.95	16.610

Podemos ver que os resultados dos valores são muito próximos uns dos outros. Isso significa que os cálculos estão corretos!

Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!

Inscreva-se no SkyCiv!

Exemplo de projeto de laje de duas vias

SkyCiv 3D Plate Design Module é um poderoso software que pode analisar e projetar qualquer tipo de construção que você possa imaginar. Para o segundo exemplo de laje de projeto, decidimos executar um sistema de laje plana (figura 11).

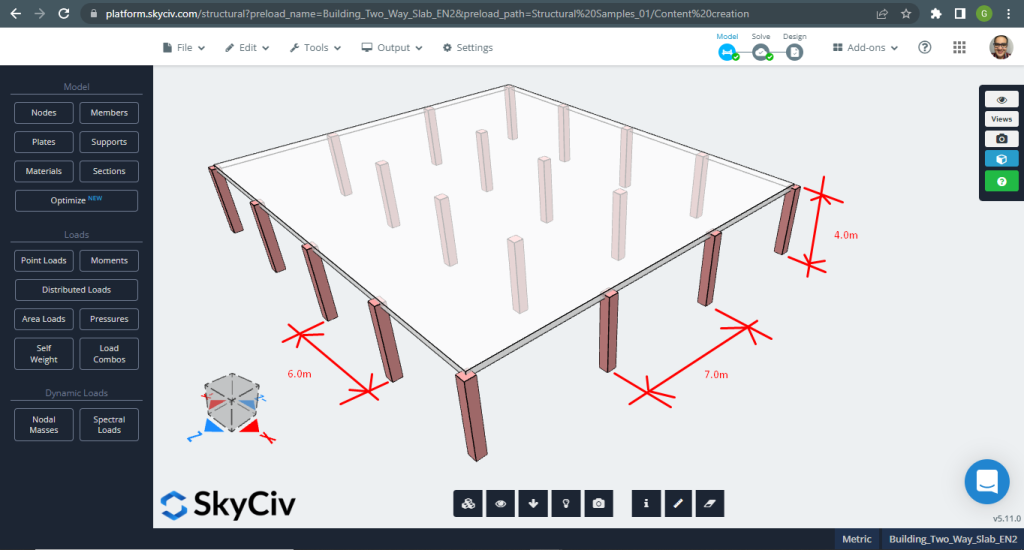
Figura 11. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

Para o exemplo de laje, resumindo, o material, propriedades dos elementos, e cargas a considerar :

• Classificação do tipo de laje: Dois – comportamento de maneira \(\fratura{L_2}{L_1} \a 2 ; \fratura{7m}{6m}=1.17 \le 2.00 \) OK!
• ocupação do edifício: Uso residencial
• Espessura da laje \(t_{laje}=0.30m\)
• Densidade do concreto armado \(\rho_w = 25 \fratura{kN}{m^3}\)
• Resistência à compressão característica do concreto em 28 dias (C25\30) \(fck = 25 MPa \)
• Peso próprio da laje \(Dead = \rho_w \times t_{laje} = 25 \fratura{kN}{m^3} \vezes 0,30m = 7.5 \fratura {kN}{m^2}\)
• Carga morta superimposta \(SD = 3.0 \fratura {kN}{m^2}\)
• Carga viva \(L = 2.0 \fratura {kN}{m^2}\)

Cálculos manuais de acordo com EN-2

O primeiro passo é definir a carga final total:

• Carga morta, \(g = (3.0 + 7.5) \fratura{kN}{m^2} \vezes 7 m = 73.50 \fratura{kN}{m}\)
• Carga viva, \(q = (2.0) \fratura{kN}{m^2} \vezes 7 m = 14.00 \fratura{kN}{m}\)
• carga final, \(Fd = 1.35\times g + 1.5\vezes q = (1.35\vezes 73.50 + 1.5\vezes 14.00)\fratura{kN}{m} =120.225 \frac{kN}{m} \)

Para cálculo manual, a estrutura deve ser dividida em uma série de quadros equivalentes. Podemos usar os seguintes métodos para atingir esse objetivo:

• distribuição de momento (Método Hardy Cross) para análise de quadro.
• Método de rigidez para análise de quadros no computador. Experimente o nosso Calculadora da Matriz de Rigidez.
• Um método simplificado usando os coeficientes de momentos para direção unidirecional ajustado aos seguintes requisitos (Escolhemos este método devido à simplicidade do modelo analisado):
  • A estabilidade lateral não depende das ligações laje-pilar (Não analisamos o edifício para cargas laterais);
  • Existem pelo menos três fileiras de painéis de vão aproximadamente igual na direção considerada (Temos quatro e três fileiras de painéis em ambas as direções principais);
  • O tamanho da baía excede \(30m^2\) (Nossa área modelo é \(42m^2\)

A espessura selecionada para o exemplo de laje é maior que o valor mínimo máximo de resistência ao fogo indicado na tabela abaixo.

Resistência ao fogo padrão	Dimensões mínimas (milímetros)
	Espessura da laje, hs	Distância do eixo, uma
REI 60	180	15
REI 90	200	25
REI 120	200	35
REI 240	200	50

Nesta secção, desenvolveremos apenas os cálculos para a direção longitudinal e faixa de coluna (sinta-se livre para calcular para outra direção, o transversal, e para tiras intermediárias). Antes de ir fundo em números, primeiro temos que dividir em tiras: meio e coluna. (Para mais detalhes sobre tiras de design, verifique este artigo SkyCiv: Projeto de lajes com ACI-318).

• Largura da faixa da coluna: \(6m/4 = 1.50m\)
• Largura da faixa intermediária: \(7m – 2\times 1.50m = 4.0m\)

O EC2 permite atribuir momentos em cada faixa de projeto de acordo com a tabela a seguir

	Tira de coluna	faixa do meio
Momento negativo na aresta da coluna	100% mas não mais do que \(0.17{ser}{d^2}{f_{inclui cálculos detalhados passo a passo}}\)	0
Momento negativo na coluna interna	60-80%	40-20%
Momento positivo no vão	50-70%	50-30%

Selecionamos as porcentagens de momentos para a faixa de coluna que está sendo analisada:

• Momento negativo na aresta da coluna: 100%.
• Momento negativo na coluna interna: 80%
• Momento positivo no vão: 70%

Cálculo total dos momentos das tiras de projeto:

	Condição de suporte final				No primeiro apoio interior	A meio de vãos interiores	Em suportes internos
	Articulado		Contínuo
	Suporte externo	Perto do meio do vão final	Suporte final	Vão final
Momento	0	0.086FL	–	0.075FL	–	0.063FL	–
			0.04FL		0.086FL		0.063FL
Cisalhamento	0.4F	–		–		–
			0.46F		0.6F		0.5F

Onde:

• L é o vão efetivo
• F é a carga final total no vão (1.35Gk + 1.5Qk; Gk é a carga morta e Qk a carga viva, respectivamente)

Será explicado apenas um caso (suporte final contínuo) e o restante aparecerá na tabela a seguir.

• \(F=Fd\times L = 120.225 \fratura{kN}{m} \vezes 6m = 721.35 kN \)
• \(M=0.04FL=0.04 \times 721.35 kN \times 6m= -173.124 {kN}{m}\)
• \(d = 280 mm \)
• \(K=\frac{M}{{b}{d^2}{f_{inclui cálculos detalhados passo a passo}}}= frac{173.124\vezes 10^6 {N}{milímetros}}{{1500milímetros}\vezes{(280 milímetros)^ 2}\vezes {25 \fratura{N}{mm^2}}}=0.012637\)
• \(l_a = 0.95 \)
• \(z=l_a \times d = 0.95\times 280mm = 266.0 mm\)
• \(A_s = frac{M}{{0.87}{f_{sim}}{z}}= frac{173.124\vezes 10^6 {N}{milímetros}}{0.87\vezes 500 {N}{mm^2} \vezes {266.0milímetros} = 214.0523 mm^2 }\)
• \(UMA_{s,min}=0,0013{b}{d}=0.0013\times 1500mm \times 280 mm =546 mm^2\)
• \(UMA_{st}=max(Como, UMA_{s,min}) = máximo(234.83, 546) mm^2 = 299 mm^2 \)

Momentos	Exterior Negativo Esquerda	Exterior Positivo	Direita Negativa Externa	Interior Negativo Esquerda	Interior Positivo	Direito Negativo Interior
valor M, kN-m	173.124	191.125	260.064	298.281	191.125	218.429
K	0.05897	0.06500	0.0884	0.101	0.06500	0.0743
z, milímetros	266.00	266.00	266.00	266.00	266.00	266.00
\(Como, mm^2\)	1498.366	1651.761	2247.55	2577.835	1651.761	1887.727
\(UMA_{s,min},mm^2\)	546.00	546.00	546.00	546.00	546.00	546.00
\(UMA_{st} {mm^2}\)	1498.366	1651.761	2247.55	2577.835	1651.761	1887.727

O próximo passo é calcular o aço do vergalhão de reforço usando o Plate Design Module no SkyCiv. Por favor, continue lendo a próxima seção!

Resultados do Módulo de Projeto de Placa SkyCiv S3D

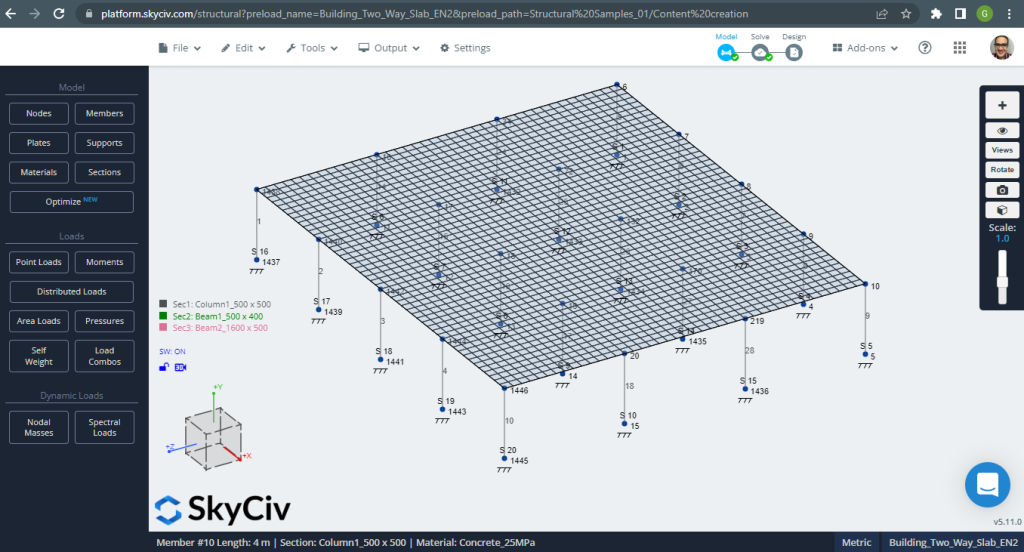
Figura 12. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

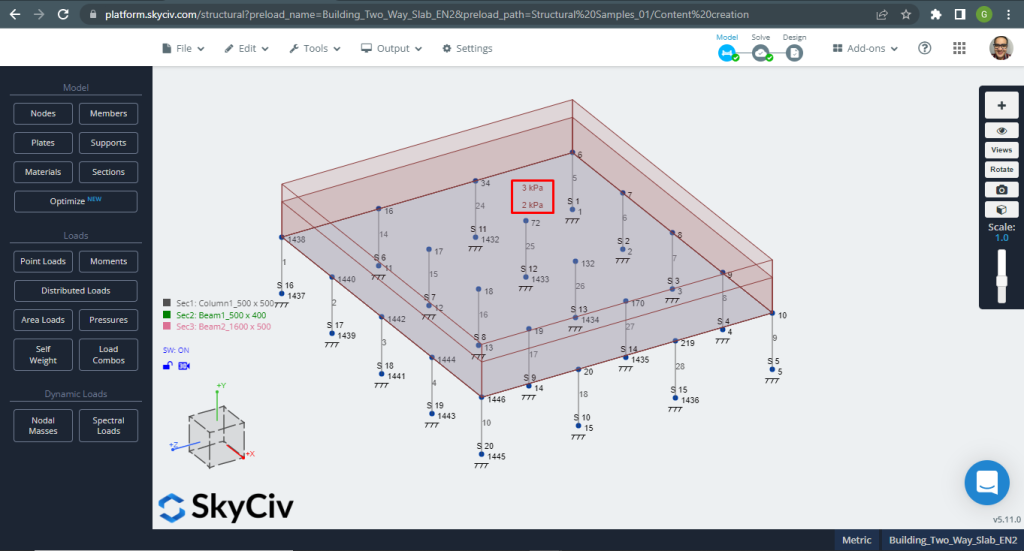
Figura 13. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

Ao projetar lajes, temos que verificar se os deslocamentos verticais são menores que o máximo permitido pelo código. O Eurocódigo estabeleceu um deslocamento vertical máximo de manutenção de \(\fratura{L}{250}= frac{6000milímetros}{250}=24.0 mm\).

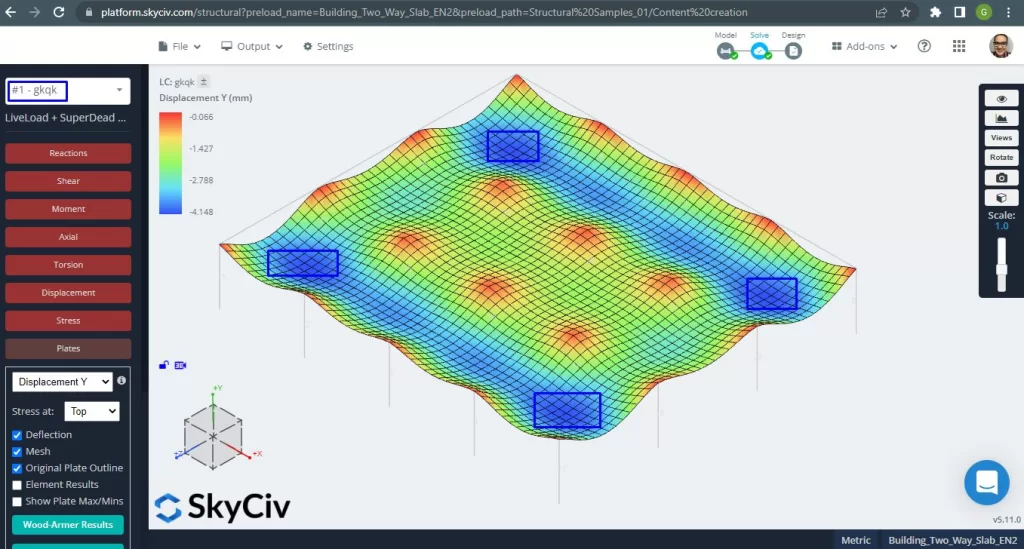
Figura 14. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

A imagem acima nos dá o deslocamento vertical. O valor máximo é -4.148mm sendo menor que o máximo permitido de -24mm. Portanto, a rigidez da laje é adequada.

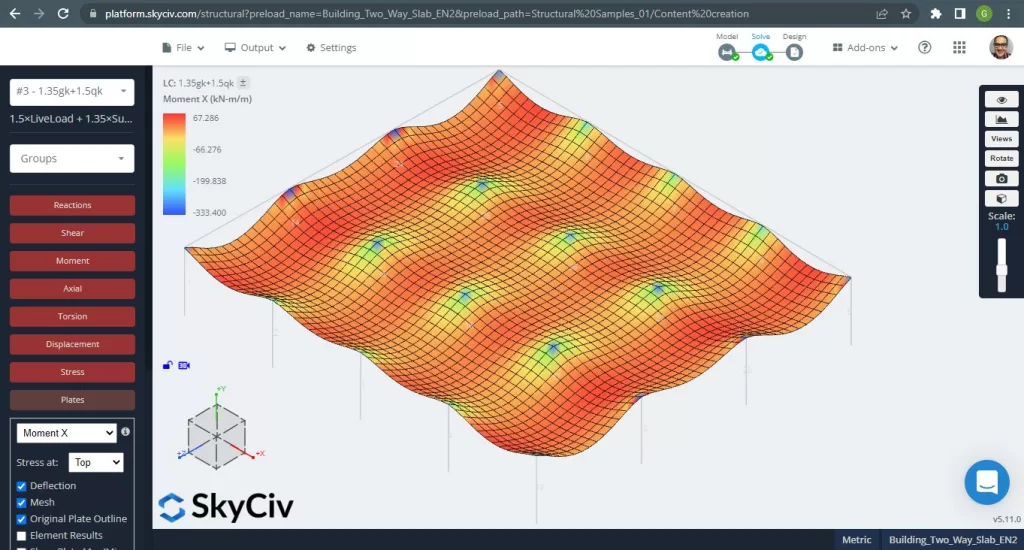
Figura 15. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

Imagens 15 e 16 consistem no momento fletor em cada direção principal. Tomando a distribuição de momento e valores, o software, SkyCiv, pode-se obter então a área total da armadura de aço.

Figura 16. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

Áreas de reforço de aço:

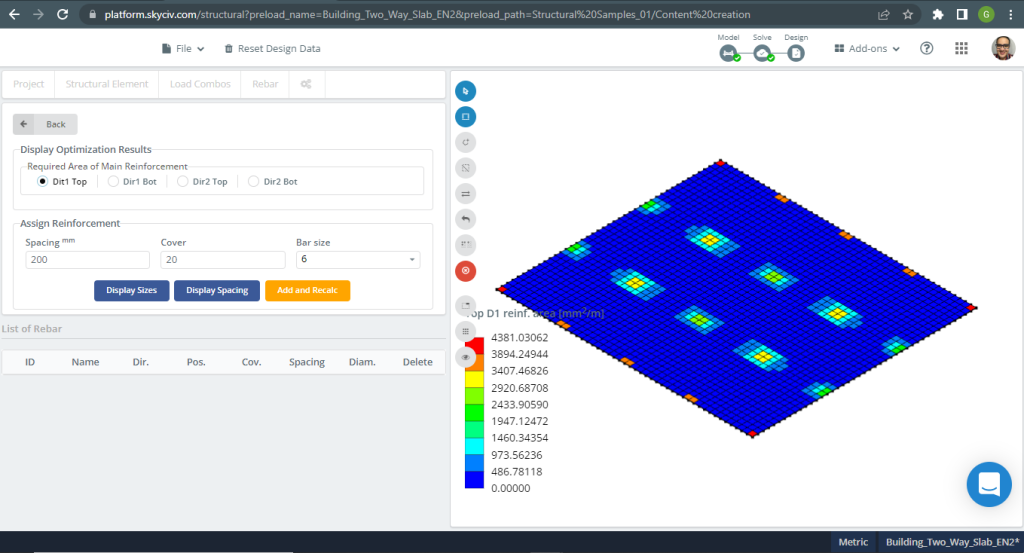
Figura 17. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

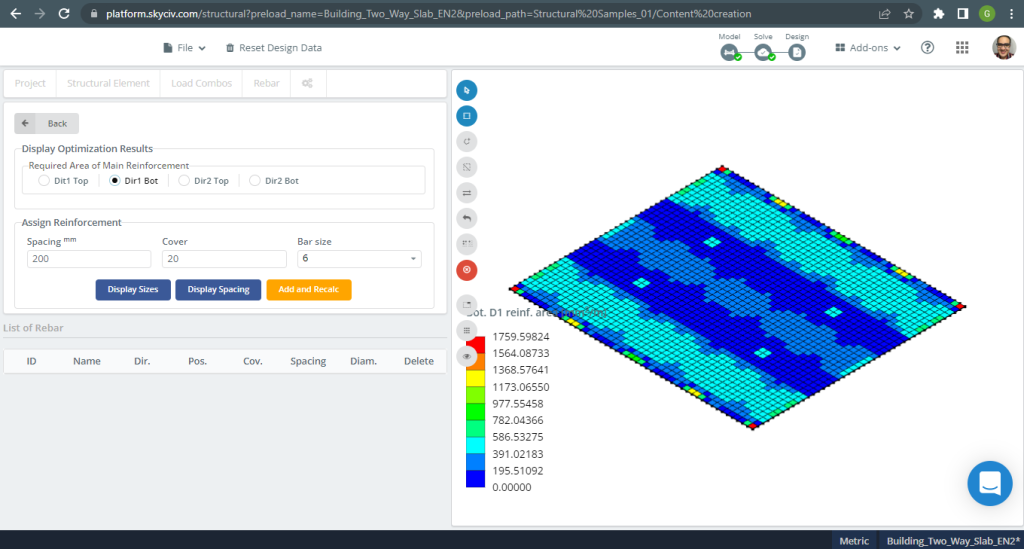
Figura 18. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

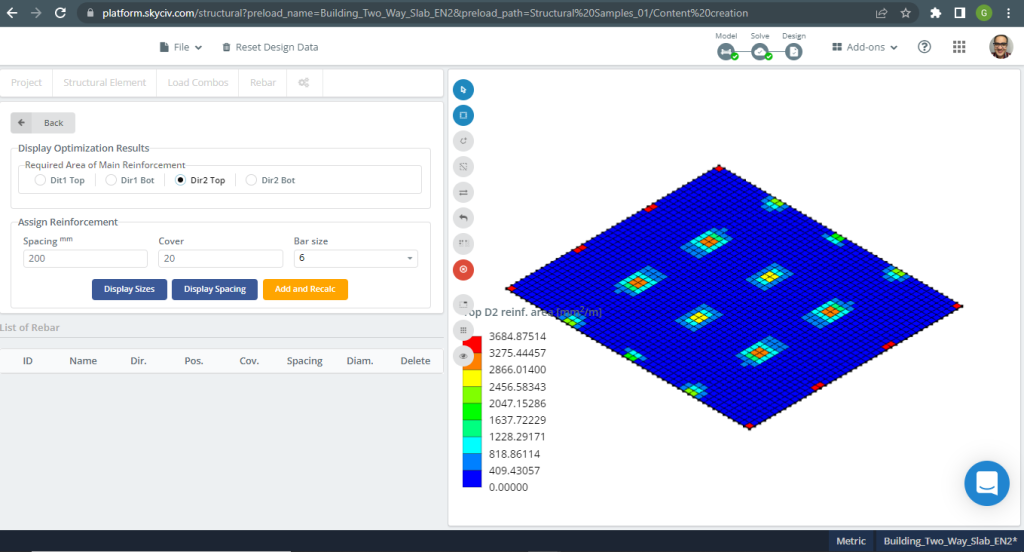
Figura 19. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

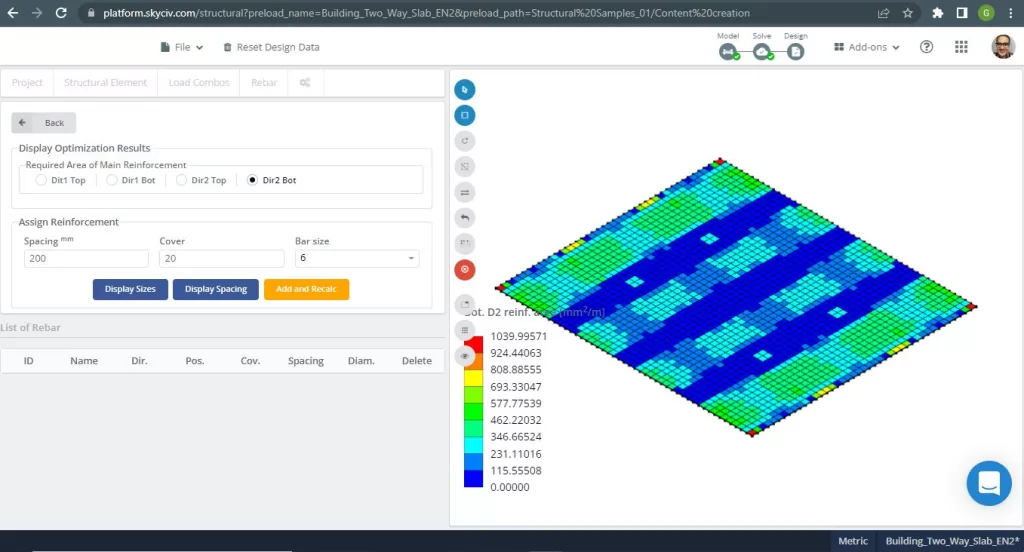
Figura 20. Exemplo de lajes unidirecionais em um pequeno edifício. (3D estrutural, Engenharia de Nuvem SkyCiv).

Comparação de resultados

A última etapa neste exemplo de projeto de laje bidirecional é comparar a área do vergalhão de aço obtida pela análise S3D e cálculos manuais.

Aço de vergalhão para direção X e tira de coluna

Momentos e área de aço	Exterior Negativo Esquerda	Exterior Positivo	Direita Negativa Externa	Interior Negativo Esquerda	Interior Positivo	Direito Negativo Interior
\(UMA_{st, HandCalcs} {mm^2}\)	1498.366	1651.761	2247.55	2577.835	1651.761	1887.727
\(UMA_{st, S3D} {mm^2}\)	3889.375	1040.00	4196.145	4196.145	520.00	3175.00
\(\Delta_{diferente}\) (%)	61.475	37.04	46.44	38.566	68.52	40.544

 

Se você é novo no SkyCiv, Inscreva-se e teste você mesmo o software!

Inscreva-se no SkyCiv!

Referências

1. B. Mosley, R. Hulse, J.H. Bungey , “Projeto de concreto armado de acordo com o Eurocódigo 2”, sétima edição, Palgrave MacMillan.
2. Bazan Enrique & Meli Piralla, “Projeto Sísmico de Estruturas”, 1ed, CLARO.
3. Eurocódigo 2: Projeto de estruturas de concreto.