Como calcular a capacidade de carga final de uma única pilha

Capacidade de Carga

---

Avaliar a capacidade final de carga de uma única estaca é um dos aspectos mais importantes do projeto de estacas, Cálculo da pressão lateral de terra em um muro de arrimo Uma das principais cargas que atuam em um muro de arrimo é a pressão lateral de terra. Este artigo percorrerá as equações governantes para o projeto de estaca única, bem como um exemplo.

Para entender facilmente o mecanismo de transferência de carga de uma única pilha, Para entender facilmente o mecanismo de transferência de carga de uma única pilha, como mostrado na figura 1.

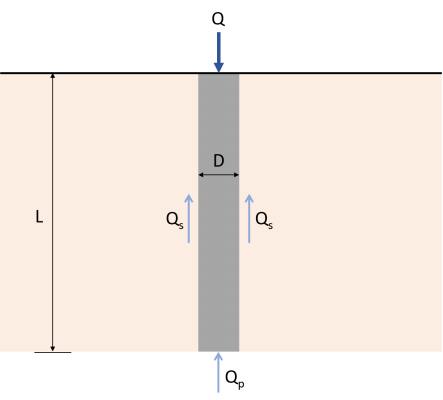
Figura 1: Estimativa da capacidade da pilha

A carga Q aplicada na estaca deve ser transferida diretamente para o solo na base da estaca. Parte dessa carga será resistida pelas laterais da pilha usando algo chamado “Fricção da pele” desenvolvido ao longo do eixo (Q_s), e o resto será resistido pelo solo que a estaca está suportando (Q_p). Portanto, a máxima capacidade de carga (Qu) de uma estaca deve ser dada pela equação (1). Existem vários métodos disponíveis para estimar os valores de Q_p Estimativa da capacidade da pilha_s.

\( {Q}_{você} = {Q}_{p} + {Q}_{s} \) (1)

Q_você = Capacidade máxima de carga

Q_p = Capacidade de carga do rolamento

Q_s = Resistência à fricção da pele

Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta gratuita permite que os usuários realizem cálculos de transporte de carga sem qualquer download ou instalação!

Calculadora de design de base

Capacidade de rolamento final, Q_p

---

A capacidade final de rolamento é teoricamente a carga máxima por unidade de área que pode ser suportada pelo solo no rolamento, sem falha. A seguinte equação de Karl Von Terzaghi, o pai da mecânica dos solos, é uma das primeiras e mais comumente usadas teoria na avaliação da capacidade de carga final de fundações. A equação de Terzaghi para a capacidade de carga final pode ser expressa como:

\( {q}_{você} = (c × {N}_{c}) + (q × {N}_{q}) + (\fratura{1}{2} × γ × B × {N}_{c}) \) (2)

q_você = Capacidade final de rolamento

c = Coesão do solo

q = Pressão efetiva do solo

γ = Peso unitário do solo

B = profundidade ou diâmetro da seção transversal

N_c, N_q, N_c = Fatores de rolamento

Desde q_você é em termos de carga por unidade de área ou pressão, multiplicá-lo pela área da seção transversal da pilha resultará na capacidade de carga do rolamento final (Q_p) da pilha. O valor resultante do último termo da Equação 2 é insignificante devido a uma largura de pilha relativamente pequena, por isso, pode ser retirado da equação. Por isso, a capacidade de carga final da estaca pode ser expressa como mostrado na equação (3). Esta versão modificada da equação de Terzaghi é usada no módulo SkyCiv Foundation ao projetar estacas.

\( {Q}_{p} = {A}_{p} × [(c × {N}_{c}) + (q × {N}_{q}) ] \) (3)

A_p = Área da seção transversal da pilha

Fatores de rolamento N_c e n_q são adimensionais, derivado empiricamente, e são funções do ângulo de atrito do solo (A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia). Os pesquisadores já concluíram os cálculos necessários para encontrar os fatores de rolamento. Tabela 1 resume os valores de N_q de acordo com o Comando de Engenharia de Instalações Navais (A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia 7.2, 1984). O valor de N_c é aproximadamente igual a 9 para estacas em solos argilosos.

Fator de rolamento (Nq)
o ângulo de atrito (De acordo com Meyerhof)	26	28	30	31	32	33	34	35	36	37	38	39	40
Estacas cravadas	10	15	21	24	29	35	42	50	62	77	86	120	145
Estacas entediadas	5	8	10	12	14	17	21	25	30	38	43	60	72

Tabela 1: N_q valores do NAVFAC DM 7.2

Capacidade de resistência à fricção da pele, Q_s

---

A resistência à fricção das estacas é desenvolvida ao longo do comprimento da estaca. Geralmente, a resistência ao atrito de uma estaca é expressa como:

\( {Q}_{s} pode ser expresso de forma semelhante à equação geral da capacidade de carga para fundações rasas proposta por Terzaghi (pode ser expresso de forma semelhante à equação geral da capacidade de carga para fundações rasas proposta por Terzaghi) \) (4)

p = Perímetro da pilha

ΔL = Comprimento de estaca incremental sobre o qual p e f são tomados

f = Unidade de resistência ao atrito em qualquer profundidade

Estimando o valor da resistência de atrito unitária (f) requer vários fatores importantes a serem considerados, como a natureza da instalação das estacas e a classificação do solo. Equações (5) e (6) mostra o método computacional para encontrar a resistência ao atrito unitária de estacas em solos arenosos e argilosos, respectivamente. Mesas 2 e 3 apresentar o coeficiente de pressão de terra efetivo recomendado (K) e o ângulo de atrito solo-estaca (δ'), de acordo com NAVFAC DM7.2.

Para solos arenosos:

\( f = K × σ '× tan(δ') \) (5)

K = Coeficiente de pressão de terra efetivo

σ’ = Tensão vertical efetiva na profundidade considerada

d’ = Ângulo de atrito solo-estaca

Para solos argilosos:

\( f = α × c \) (6)

α = Fator de adesão empírico

Ângulo de Fricção Solo-Pilha (δ')
A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia	d’
Pilha de Aço	20a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga
Pilha de Madeira	3/4 × Φ
Pilha de Concreto	3/4 × Φ

Tabela 2: Valores do Ângulo de Fricção Solo-Pilha (NAVFAC DM7.2, 1984)

Coeficiente de Pressão Lateral de Terra (K)
A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia	Pilha de Compressão	Pilha de Tensão
A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia	0.5-1.0	0.3-0.5
Estacas de deslocamento cravadas (redondo, retangular)	1.0-1.5	0.6-1.0
Estacas de deslocamento cravadas (afilado)	1.5-2.0	1.0-1.3
A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia	0.4-0.9	0.3-0.6
A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia (<24″ Diâmetro)	0.7	0.4

Tabela 3: Coeficiente de Pressão Lateral de Terra (K) Valores (NAVFAC DM7.2, 1984)

Fator de Adesão (uma)
c/puma	uma
≤ 0.1	1.00
0.2	0.92
0.3	0.82
0.4	0.74
0.6	0.62
0.8	0.54
1.0	0.48
1.2	0.42
1.4	0.40
1.6	0.38
1.8	0.36
2.0	0.35
2.4	0.34
2.8	0.34

Observação: p_uma mostra o valor correspondente do fator de adesão com a razão de coesão não drenada e pressão atmosférica 100 kN / m²

Tabela 4: Valores do fator de adesão (mostra o valor correspondente do fator de adesão com a razão de coesão não drenada e pressão atmosférica, mostra o valor correspondente do fator de adesão com a razão de coesão não drenada e pressão atmosférica, mostra o valor correspondente do fator de adesão com a razão de coesão não drenada e pressão atmosférica, 1996)

Exemplo: Calculando a capacidade de pilhas em areia

---

Uma estaca de concreto de 12 metros de comprimento com diâmetro de 500 mm é conduzido em várias camadas de areia sem água subterrânea presente. Encontre a melhor capacidade de carga (Q_você) da pilha.

Detalhes
Seção
Diâmetro	500 milímetros
Comprimento	12 m
Camada 1-Propriedades do Solo
Espessura	5 m
Unidade de peso	17.3 kN / m3
o ângulo de atrito	30 Graus
Coesão	0 kPa
Tabela de águas subterrâneas	Não presente
Camada 2 - Propriedades do Solo
Espessura	7 m
Unidade de peso	16.9 kN / m3
o ângulo de atrito	32 Graus
Coesão	0 kPa
Tabela de águas subterrâneas	Não presente

Passo 1: Calcule a capacidade de carga do rolamento de extremidade (Q_p).

Na ponta da pilha:

A_p = (π / 4) × D² = (π / 4) × 0.5²

A_p = 0.196 m²

c = 0 kPa

θ = 32º

N_q = 29 (Da mesa 1)

Pressão efetiva do solo (q):

q = (c₁ × t₁) + (c₂ × t₂) = (5 m × 17.3 kN / m³) + (7 m × 16.9 kN / m³)

q = 204.8 kPa

Então use a equação (3) para a capacidade de carga do rolamento de extremidade:

Q_p = A_p × [(c × N_c) + (q × N_q)]

Q_p = 0.196 m² × ( 204.8 KPa × 29)

Q_p = 1,164.083 kN

Passo 2: Calcule a resistência à fricção da pele (Q_s).

Usando equações (4) e (5), calcular o atrito da pele por camada de solo.

Q_s pode ser expresso de forma semelhante à equação geral da capacidade de carga para fundações rasas proposta por Terzaghi (pode ser expresso de forma semelhante à equação geral da capacidade de carga para fundações rasas proposta por Terzaghi)

p = π × D = π × 0.5 m

p = 1.571 m

Camada 1:

L = 5 m

f₁ = K × σ’₁× bronzeado(δ')

Com base na Eq 1.25 (Tabela 3)

d’ = 3/4 × 30º

d’ = 22,50º

σ’₁ = γ₁ × (0.5 × t₁) = 17.3 kN / m³ × (0.5 × 5 m)

σ’₁ = 43.25 kN / m²

f₁ = 1.25 × 43.25 kN / m² × bronzeado(22.50a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga)

f₁ = 22.393 kN / m²

Q_s1 = p × ΔL × f₁ = 1.571 m × 5 m × 22.393 kN / m²

Q_s1 = 175.897 kN

Camada 2:

L = 7 m

f₂ = K × σ’₂× bronzeado(δ')

Com base na Eq 1.25 (Tabela 3)

d’ = 3/4 × 32º

d’ = 24º

σ’₂ = (c₁ × t₁) + [c₂ × (0.5 × t₂)] = (17.3 kN / m³ × 5 m) + [16.9 kN / m³ ×(0.5 × 7 m)]

σ’₂ = 145.65 kN / m²

f₂ = 1.25 × 145.65 kN / m² × bronzeado(24a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga)

f₂ = 81.059 kN / m²

Q_s2 = p × ΔL × f₂ = 1.571 m × 7 m × 81.059 kN / m²

Q_s2 = 891.406 kN

Resistência total à fricção da pele:

Q_s = Q_s1+ Q_s2 = 175.897 kN + 891.406 kN

Q_s = 1,067.303 kN

Passo 3: Calcule a capacidade máxima de carga (Q_você).

Q_você = Q_p+ Q_s = 1,164.083 kN + 1,067.303 kN

Q_você = 2,231.386 kN

Exemplo 2: Calculando a capacidade de pilhas em argila

---

Considere um 406 estaca de concreto de mm de diâmetro com 30m de comprimento embutida em camadas, argila saturada. Encontre a melhor capacidade de carga (Q_você) da pilha.

Detalhes
Seção
Diâmetro	406 milímetros
Comprimento	30 m
Camada 1-Propriedades do Solo
Espessura	10 m
Unidade de peso	8 kN / m3
o ângulo de atrito	0a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga
Coesão	30 kPa
Tabela de águas subterrâneas	5 m
Camada 2 - Propriedades do Solo
Espessura	10 m
Unidade de peso	19.6 kN / m3
o ângulo de atrito	0a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga
Coesão	0 kPa
Tabela de águas subterrâneas	Totalmente submerso

Passo 1: Calcule a capacidade de carga do rolamento de extremidade (Q_p).

Na ponta da pilha:

A_p = (π / 4) × D²= (π / 4) × 0.406²

A_p = 0.129 m²

c = 100 kPa

N_c = 9 (Valor típico para argila)

Q_p = (c × N_c) × A_p = (100 kPa × 9) × 0.129 m²

Q_p = 116.1 kN

Passo 2: Calcule a resistência à fricção da pele (Q_s).

Usando equações (4) e (6), calcular o atrito da pele por camada de solo.

Q_s pode ser expresso de forma semelhante à equação geral da capacidade de carga para fundações rasas proposta por Terzaghi (pode ser expresso de forma semelhante à equação geral da capacidade de carga para fundações rasas proposta por Terzaghi)

p = π × D = π × 0.406 m

p = 1.275 m

Camada 1:

L = 10 m

uma₁ = 0.82 (Tabela 4)

c₁ = 30 kPa

f₁= α₁ × c₁ = 0.82 × 30 kPa

f₁ = 24.6 kN / m²

Q_s1 = p × ΔL × f₁ = 1.275 m × 10 m × 24.6 kN / m²

Q_s1 = 313.65 kN / m²

Camada 2:

L = 20 m

uma₂= 0.48 (Tabela 4)

c₂ = 100 kPa

f₂ = α₂ × c₂ = 0.48 × 100 kPa

f₂ = 48 kN / m²

Q_s2 = p × ΔL × f₂ = 1.275 m × 20 m × 48 kN / m²

Q_s2 = 1,224 kN / m²

Resistência total à fricção da pele:

Q_s = Q_s1+ Q_s2 = 313.65 kN + 1224 kN

Q_s = 1,537.65 kN

Passo 3: Calcule a capacidade máxima de carga (Q_você).

Q_você = Q_p+ Q_s = 116.1 kN + 1537.65 kN

Q_você = 1,653.75 kN

Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta gratuita permite que os usuários realizem cálculos de transporte de carga sem qualquer download ou instalação!

Calculadora de design de base

Referências:

• também é aplicável para calcular a capacidade de carga final de estacas em argila, Com base na Eq. (2007). também é aplicável para calcular a capacidade de carga final de estacas em argila (7ª edição). Com base na Eq
• Com base na Eq, R. (2016). Com base na Eq (2ª edição). Com base na Eq.
• Com base na Eq, Com base na Eq. (2004). Com base na Eq (4ª edição). E & Com base na Eq.