Um passo a passo dos cálculos para projetar uma base isolada (AS 3600 2018)
A fundação é um sistema de construção essencial que transfere as forças da coluna e da parede para o solo de suporte. O engenheiro pode optar por um sistema de fundação raso ou profundo com base nas características do solo e nas cargas do edifício..
Módulo SkyCiv FoundationDesign inclui analisar e projetar sapatas isoladas em conformidade com os padrões australianos (AS 3600 2009 & 2018).
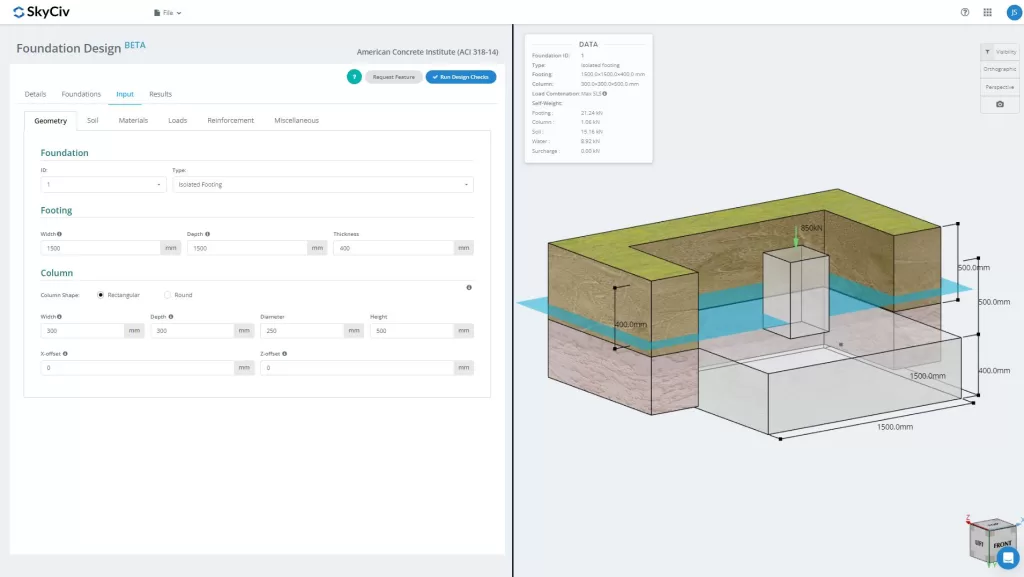
Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta permite aos usuários realizar cálculos de carga sem qualquer download ou instalação!
Projeto de uma base isolada
Requisitos de Dimensão
Para determinar as dimensões de uma sapata isolada, serviço ou cargas não fatoradas, como ação permanente (G), ação imposta (Q), ação do vento (Cvocê), ação do terremoto (Evocê), e Svocê será aplicado usando combinações de carga, conforme definido por AS 3600. Qualquer combinação de carga governar será considerada a carga do projeto, e é comparado com a pressão do solo permitida, conforme mostrado na Equação 1.
\(\texto{q}_{\texto{uma}} = frac{\texto{P}_{\texto{n}}}{\texto{A}} \seta direita \) Equação 1
quma = pressão permitida do solo
Pn = cargas de design de nível de serviço
A = área de fundação
As dimensões da sapata podem ser inicialmente estimadas resolvendo a área da fundação (A) usando equação 1.
\(\texto{A} = frac{\texto{P}_{\texto{n}}}{\texto{q}_{\texto{uma}}} \seta direita \) Equação 1a
Tesoura unidirecional
A cisalhamento unidirecional estado limite, também conhecido como cisalhamento de flexão, reconhece que a sapata pode falhar em cisalhamento semelhante a uma viga larga ao longo de um plano de cisalhamento crítico localizado a uma distância “d” da face da coluna (Figura 1), baseado em Cláusula AS3600 8.2.7.1
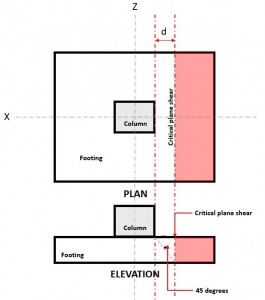
Figura 1. Plano de cisalhamento crítico de cisalhamento unidirecional
A Mão única Cisalhamento Demanda ou Vvocê é calculado assumindo que a sapata está em balanço longe do pilar onde a área vermelha é indicada na Figura 1.
A Mão única Cisalhamento Capacidade ou ϕVuc é definido como a resistência ao cisalhamento final e calculado usando a Equação 2 por AS3600-09Cl 8.2.7.1.
\( \phi texto{V}_{uc} =phibeta_{1} \vezes beta_{2} \vezes beta_{3} \vezes b_{v} \vezes d_{o} \vezes f_{cv} \vezes A_{st}^{\fratura{2}{3}} \seta direita \) Equação 2 (Eq AS3600. 8.2.7.1)
ϕ = fator de cálculo de cisalhamento
b1= 1.1(1.6 – do/1000) ≥ 1.1 ou 1.1(1.6(1-do/1000) ≥ 0.8
b2 = 1, para barras sujeitas a flexão pura; ou
=1-(N*/3.5Ag) ≥ 0 para membro sujeito a tensão axial; ou
=1-(N*/14Ag) para barras sujeitas a compressão axial
b3 = 1, ou pode ser tomado como –
2do/umav mas não maior que 2
umav = distância da seção na qual o cisalhamento está sendo considerado até a face do apoio mais próximo
fcv = f'c1/3 ≤ 4 MPa
Ast = área da seção transversal da armadura longitudinal
A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender aos requisitos de projeto do AS 3600-09:
\(\texto{V}_{\texto{você}} \leq phi text{V}_{\texto{uc}} \seta direita \) Equação 3 (por AS3600Cl. 8.2.5)
Fundação SkyCiv, em conformidade com a equação 3, calcula a taxa de utilidade de cisalhamento unidirecional (Equação 4) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Taxa de utilidade} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 4
Cisalhamento de duas vias
A Cisalhamento de duas vias estado limite, também conhecido como punção, estende sua seção crítica a uma distância “d/2” da face da coluna e ao redor do perímetro da coluna (Figura 2) baseado em Cláusula AS3600 9.2.3(uma).
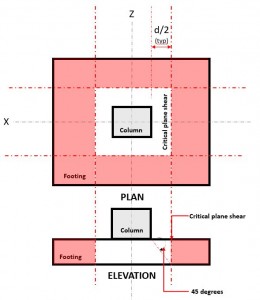
Figura 2. Plano de cisalhamento crítico de cisalhamento bidirecional
A Dois caminhosouvir Demanda ou Vvocê ocorre no plano de cisalhamento crítico, localizado a uma distância de “d/2” onde o (vermelho) área hachurada, conforme indicado na Figura 2.
A Duas vias Capacidade de cisalhamento ou ϕVuo é definido como a resistência ao cisalhamento final e calculado usando a Equação 5 baseado em Cláusula AS3600 9.2.3
\( \phi V_{uo} = phi vezes você vezes f_{cv} \vezes d rightarrow \) Equação 5 (AS3600Cl. 9.2.3(uma))
fcv = 0.17(1 + 2/bh) √f’c ≤ 0,34√f’c
bh = razão entre o comprimento da coluna no eixo Z sobre o eixo X
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal (milímetros)
u = comprimento do perímetro de cisalhamento crítico (milímetros)
A demanda de cisalhamento e a capacidade de cisalhamento devem atender à seguinte equação para atender aos requisitos de projeto do AS 3600:
\(\texto{V}_{\texto{você}} \leq phi text{V}_{\texto{uo}} \seta direita \) Equação 6 (por AS3600Cl. 8.2.5)
Fundação SkyCiv, em conformidade com a equação 6, calcula a taxa de utilidade de cisalhamento bidirecional (Equação 7) considerando a demanda de cisalhamento sobre a capacidade de cisalhamento.
\( \texto{Taxa de utilidade} = frac{\texto{Demanda de cisalhamento}}{\texto{Capacidade de cisalhamento}} \seta direita \) Equação 7
Flexure
Em situação isolada, onde o módulo extrairá cada reação de carga por suporte e passará para o. Os momentos fletores são calculados em cada direção na seção 0.7umaonde o módulo extrairá cada reação de carga por suporte e passará para o distância do centro da coluna, Onde umaonde o módulo extrairá cada reação de carga por suporte e passará para o é metade da largura da coluna.
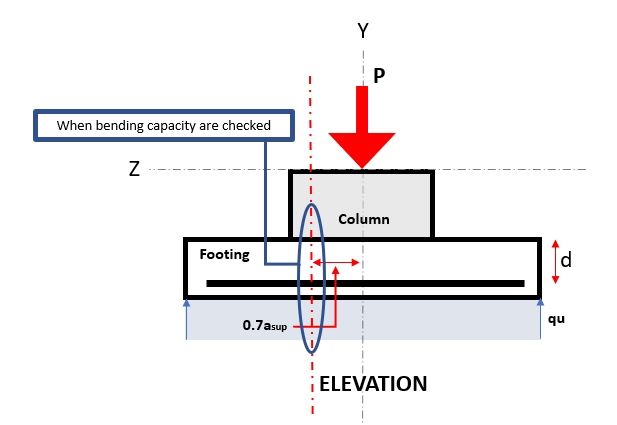
Figura 3. Seção Crítica de Flexão
A Flexural estado limite ocorre na seção de flexão crítica, localizado 0.7umaonde o módulo extrairá cada reação de carga por suporte e passará para o do centro da base (Consulte a Figura 3).
A Demanda Flexural ou Mvocê está localizado na seção de flexão crítica indicada na Figura 3, e é calculado usando a Equação 8.
\( \texto{M}^{*}= q_{você} \vezes D_{f} \times left( \fratura{ \fratura{b_{f} – b_{c}}{2} }{2} \direito)^{2} \seta direita \) Equação 8
A Capacidade Flexural ou ϕMn é calculado usando a Equação 9.
\(M_{n} = A_{st} \vezes f_{seu} \vezes d vezes esquerda(1- \fratura{0.5}{\alfa_{s}} \vezes frac{UMA_{st} \vezes f_{seu}}{b vezes d vezes f’_{c}} \direito) \seta direita \) Equação 9
ϕ = fator de projeto de flexão
b = dimensão da sapata paralela ao eixo x, (milímetros)
d = distância da fibra de compressão extrema ao centroide do reforço de tensão longitudinal, (milímetros)
Ast = área de reforço, (milímetros2)
a = profundidade do bloco de tensão retangular equivalente, (milímetros)
fsy = resistência do reforço, (MPa)
A demanda de momento e a capacidade de momento devem atender à seguinte equação para atender aos requisitos de projeto do AS 3600:
\(\texto{M}_{\texto{você}} \leq phi text{M}_{\texto{n}} \seta direita \) Equação 10 (por AS3600Cl. 8.2.5)
Fundação SkyCiv, em conformidade com a equação 10, calcula a taxa de utilidade flexural (Equação 11) tomando Flexural Demand em vez de Flexural Capacity.
\( \texto{Taxa de utilidade} = frac{\texto{Flexure Demand}}{\texto{Capacidade de Flexão}} \seta direita \) Equação 11
Reforço
A quantidade de reforço necessária é determinada pelos requisitos de resistência à flexão, com armadura mínima especificada em Cl. 21.3.1 (b)
\( \rho_{ \texto{min} } = 0.19 \vezes frac{D}{d}^{2} \vezes frac{f’_{ct.f} }{ f_{seu} } \seta direita \) Equação 12
A área do aço pode ser determinada com a seguinte equação:
\( \rho = frac{ 2.7 \vezes M^{*} }{ d^{2} } \texto{ ou } \texto{A}_{\texto{st}} = frac{ \texto{M}^{*} }{ 370 \times text{d} } \seta direita \) Equação 13
Como aconselhado por AS 3600, uma cobertura mínima de concreto de 60 milímetros para o pé é recomendado.
Verificações Adicionais
Outras verificações não mencionadas no código, incluindo verificações de pressão do solo, forças de elevação, e outras verificações de estabilidade também são verificadas.
Pressão do Solo
A determinação da pressão de base ou da interação entre o solo e a sapata depende principalmente das dimensões da sapata e da excentricidade resultante das cargas aplicadas. Dependendo do posicionamento desta excentricidade resultante, a pressão na base pode induzir compressão total ou parcial na sapata. Esta avaliação permite-nos confirmar se o solo subjacente pode suportar a totalidade das cargas transmitidas pela sapata.
Para obter um guia detalhado para calcular manualmente a pressão do solo, por favor consulte este link: Distribuição de pressão sob uma sapata de concreto retangular
A taxa de utilidade é avaliada comparando a pressão máxima do solo (estado de utilização) com a capacidade bruta permitida do solo:
\( \texto{Taxa de utilidade} = frac{\texto{Máx.. Pressão do Solo}}{\texto{Capacidade Bruta Permissível de Suporte do Solo}} \seta direita \) Equação 14
A seguir estão as diferentes maneiras de determinar os coeficientes de pressão de terra para calcular a resistência ao atrito unitária de estacas em areia
Verifica a carga axial governante que atua na sapata. Soma todas as cargas verticais, incluindo a carga do usuário e os pesos próprios da coluna, laje de pé, solo, e força de empuxo. Se a coluna sofrer uma força ascendente, os pesos próprios especificados devem contrabalançar a força ascendente; de outra forma, o projeto corre o risco de falhar devido à instabilidade.
capotamento
O tombamento da sapata é verificado somando todos os momentos em torno de um ponto da sapata, incluindo todas as forças que atuam sobre ele.. Todas as combinações de carga de serviço devem ser consideradas para verificar o momento de tombamento dominante. Geralmente, um fator de segurança de 1.5-2 é empregado para avaliar se a sapata passa na verificação de tombamento.
deslizante
Para verificar se há deslizamento, a soma das cargas resistentes horizontais apontando para a direita é dividida pela soma das cargas apontando para a esquerda.
- Resistência a cargas:
- Força horizontal devido ao atrito entre a base da sapata e o solo da subestrutura
- Pressão passiva do solo (se incluído)
- Cargas deslizantes:
- O componente horizontal da pressão ativa do solo
- O componente horizontal da pressão resultante da sobrecarga
Geralmente, um fator mínimo de segurança de 1.5 é usado. Se nenhuma força horizontal estiver atuando na base, verificar se há deslizamento não é necessário.
Módulo de design da Fundação SkyCiv
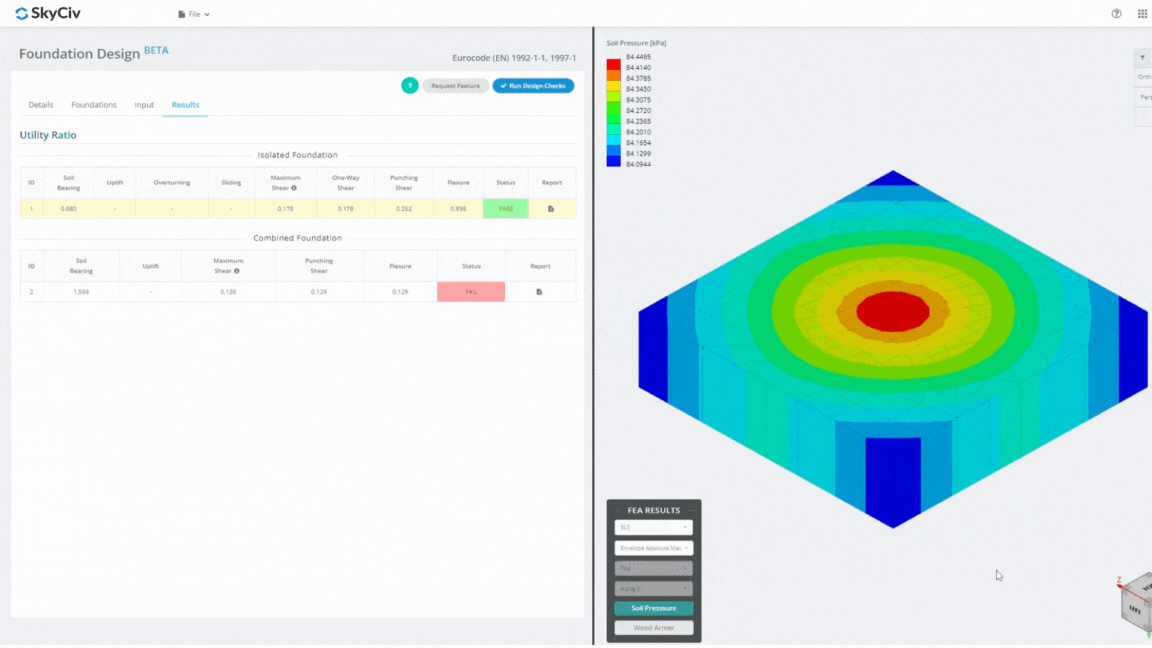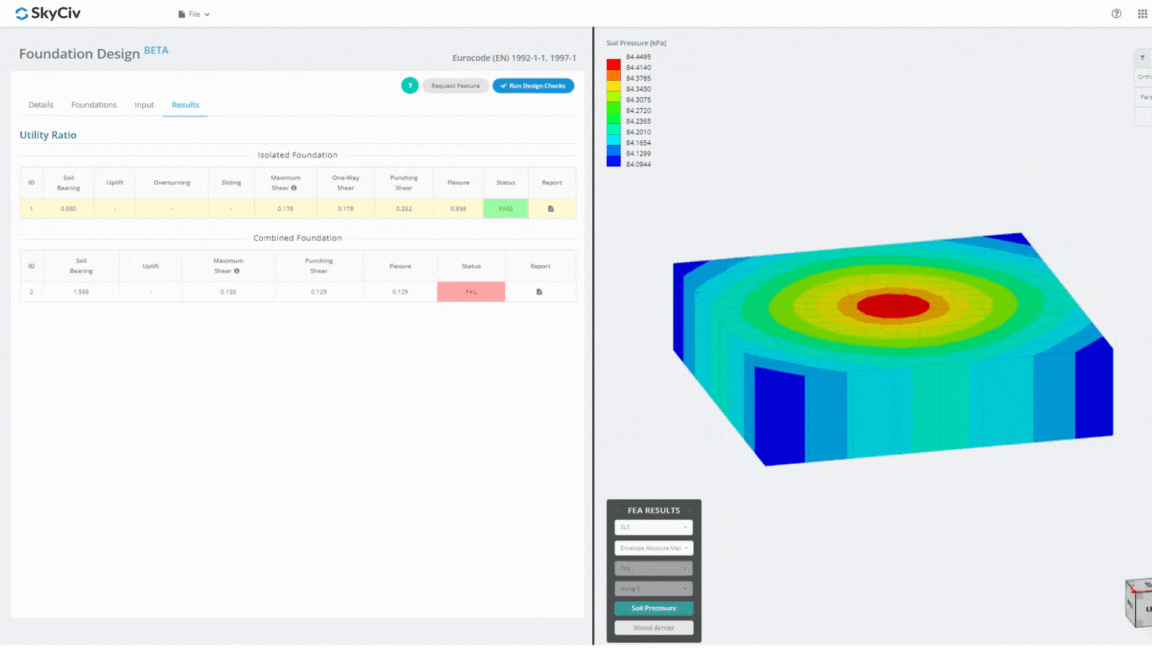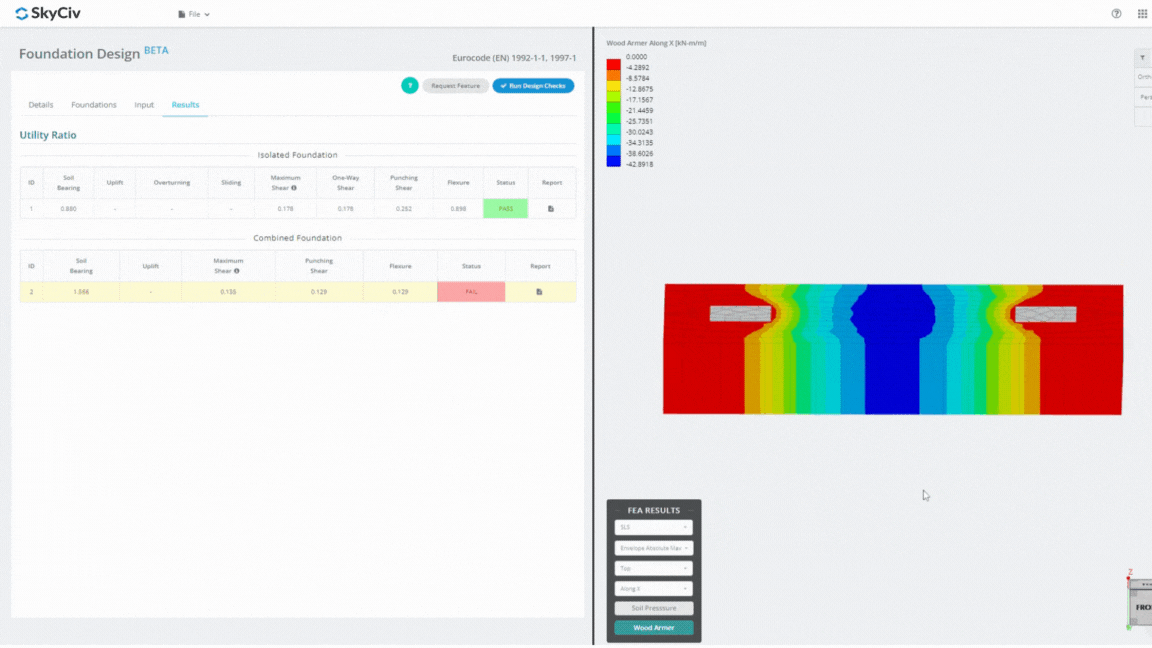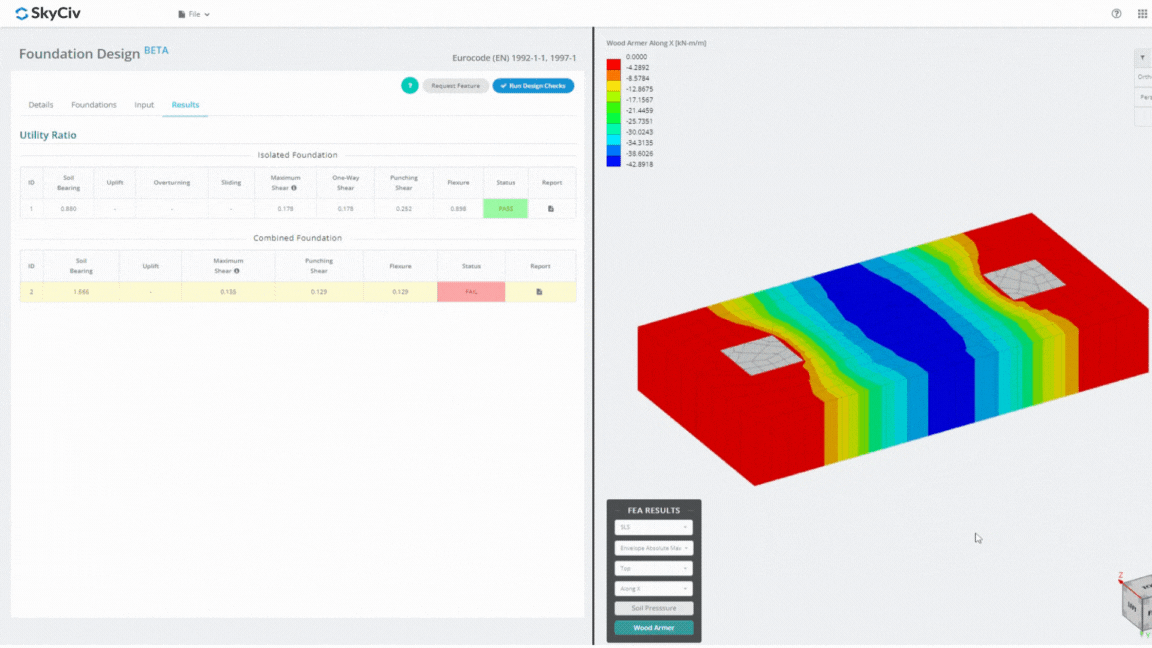
O Foundation Design Module é uma ferramenta poderosa integrada com Análise de Elementos Finitos (FEIO), capaz de realizar análises completas da pressão do solo e da armadura de madeira para verificações detalhadas de flexão. Executa todas as verificações estruturais especificadas pela ACI 318 e outras verificações mencionadas acima e as apresenta em um relatório abrangente.
Comece com a Fundação SkyCiv hoje!
Inicie o Projeto de Fundação e experimente hoje! É fácil começar, mas se precisar de mais ajuda, então não deixe de visitar nosso documentação ou entre em contato conosco!
Não é um usuário SkyCiv? Inscreva-se para um Livre 14 Dia de teste para começar!
Desenvolvedor de Produto
bacharelado (Civil), Mestrado (Civil)
Albert Pamonag
Engenheiro estrutural, Desenvolvimento de Produto
B.S. Engenharia Civil
Referências
- Conselho de Padrões Austrália. (2009) Padrão Australiano AS3600-2009.
- SJ Foster, AE Kilpatrick & RF Warner. (2011) Noções básicas de concreto armado 2ª edição.
- Taylor, Andrew, et al. O Manual de Projeto de Concreto Armado: um companheiro para ACI-318-14. American Concrete Institute, 2015.
- YC Loo & SH Chowdhury. (2013) Reforçado & Betão Protendido.




