A fundação é um elemento essencial de uma estrutura para fornecer estabilidade geral, transmitindo e distribuindo as cargas totais da estrutura ao solo.. Fundações rasas, como base isolada retangular ou quadrada, são o tipo preferido de fundação devido à simplicidade de sua construção e custo total em comparação com fundações profundas. Estimar a pressão de base afeta drasticamente o projeto e o dimensionamento da sapata. Normalmente, a relação de utilidade entre a capacidade de suporte admissível do solo e a pressão de base governante sob a sapata é a base do tamanho inicial da sapata. Uma vez que as dimensões iniciais da sapata são definidas, verificações adicionais de design para segurança e estabilidade, como cisalhamento unidirecional e bidirecional, capacidade de flexão, e verificações de comprimento de desenvolvimento, são verificados dependendo de qual código de design é usado.
Quando uma sapata é submetida a uma flexão biaxial (Mx, Mz), assume-se que a carga axial (P) está agindo em uma coordenada de excentricidade (ex, ez) onde há uma tendência de rotação a partir do centro. A interação entre o solo e a sapata depende principalmente da dimensão da sapata e da excentricidade resultante das cargas aplicadas. Dependendo da localização da excentricidade resultante, a pressão de base faz com que a sapata esteja em compressão total ou parcial. Na prática, recomenda-se projetar uma sapata em compressão total. A compressão parcial ou perda de contato entre o solo e a sapata não deve ser negligenciada, mas a maioria dos designers evita esse cenário devido à sua complexidade de cálculo. A sapata está em compressão total quando a excentricidade resultante está localizada dentro do kern ou abaixo da Zona C. A excentricidade fora da Zona C coloca a base em compressão parcial. Figura 1 mostra as diferentes zonas designadas em uma base retangular.
Este artigo deve se concentrar no cálculo de pressões de canto em diferentes classificações de zona com base em Bellos & Vestígio (2017) e S.S.. Ray's (1995) estudos.
Classificações de zona de uma base retangular
As classificações de zona de uma sapata retangular são derivadas de vários estudos de diferentes autores para desenvolver uma abordagem prática para estimar a distribuição da pressão do solo sob condições de carga esperadas. Como mostrado na figura 1, há cinco regiões diferentes (Zonas A-E) dependendo da localização da excentricidade resultante. Cada zona corresponde a um carregamento diferente, distribuição de pressão de base, e deformação. Zona C, também conhecido como kern, é o núcleo principal. É a região ideal para projetar uma sapata, resultando em compressão total na sapata. As dimensões desta região são equivalentes a 1/6 do respectivo comprimento da sapata.
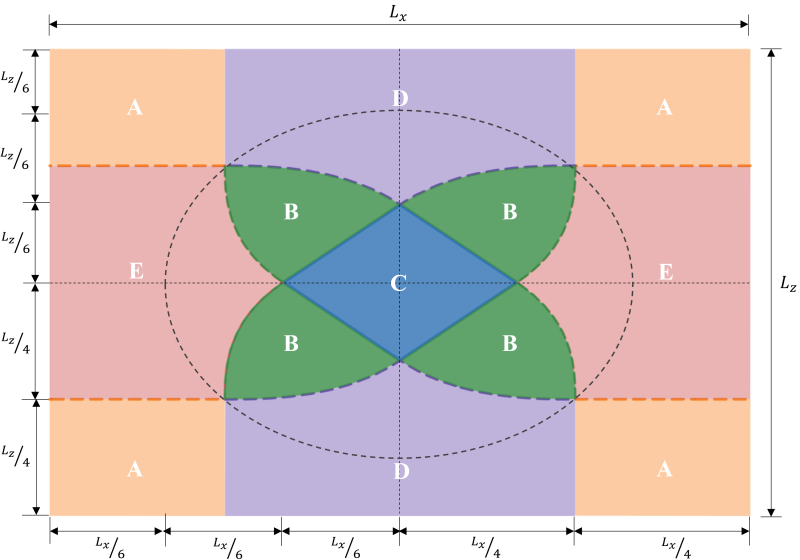
Figura 1: Classificações de zona de uma base retangular
O núcleo secundário é a área elíptica (delimitado pela linha tracejada na Figura 1) com seus semi-eixos maior e menor iguais a 1/3 do respectivo comprimento da sapata. Esta região abrange todas as zonas B & C e algumas partes das zonas D & E. O núcleo secundário resulta em uma compressão parcial da sapata. É uma boa prática manter a excentricidade dentro da zona secundária para um projeto de sapata aceitável.
A excentricidade além da zona secundária é o resultado da alta carga biaxial. Abrange toda a zona A e as partes restantes das zonas D & E. Recomenda-se evitar projetar a sapata nessas regiões, pois haverá risco de capotamento. Conseqüentemente, é aconselhável redesenhar as dimensões da sapata para este tipo de carregamento.
O seguinte enumera as fórmulas analíticas para resolver as pressões de canto em cada classificação de zona.
Zona C (Núcleo principal, zona de compressão total)
Como mencionado, este é o caso mais preferido para projetar sapatas, pois é capaz de colocar toda a base da sapata em compressão, como mostrado na figura 2. Este caso é representado por pequena excentricidade dentro do kern ou nenhuma excentricidade. Figura 2 mostra a excentricidade dentro do kern com sua pressão máxima nos cantos P3 & P4 e pressão mínima nos cantos P1 & P2.
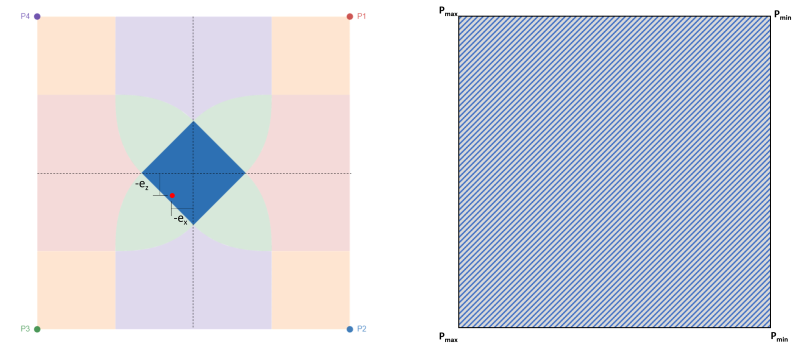
Figura 2: Excentricidade (-ex, -ez) na Zona C & área de compressão total
Máximo & pressões de canto mínimas (lindo & Vestígio, 2017):
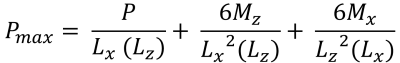
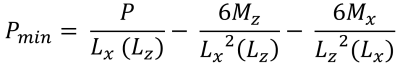
| Pressões de canto com base na excentricidade | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| +ex, +ez | Pmax | Pmax | Pmin | Pmin |
| +ex, -ez | Pmax | Pmax | Pmin | Pmin |
| -ex, -ez | Pmin | Pmin | Pmax | Pmax |
| -ex, +ez | Pmin | Pmin | Pmax | Pmax |
Zona A (zona de compressão triangular)
Este caso corresponde a quatro áreas retangulares em cada canto da sapata. Geralmente ocorre com grande excentricidade biaxial, impondo uma alta área de compressão triangular em um dos cantos, como mostrado pela região sombreada na Figura 3. Os cantos restantes perdem contato com o solo. Conseqüentemente, este caso não é aconselhável para o projeto.
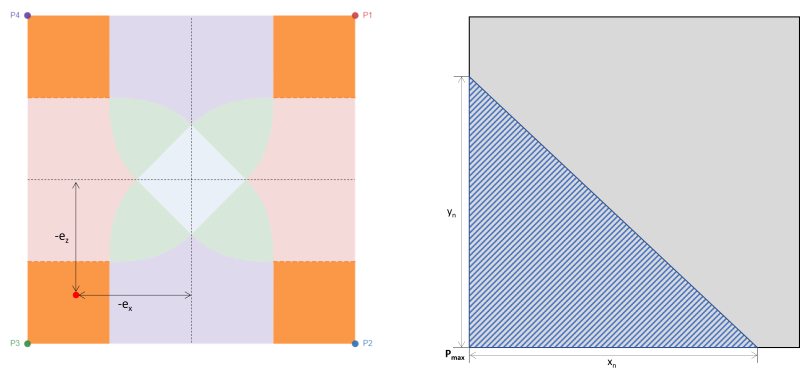Figura 3: Excentricidade (-ex, -ez) na Zona A & área de compressão triangular em torno de P3
pressão máxima (lindo & Vestígio, 2017):
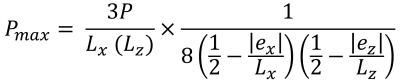
| Pressões de canto com base na excentricidade | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ex(+), ez(+) | Pmax | 0 | 0 | 0 |
| ex(+), ez(-) | 0 | Pmax | 0 | 0 |
| ex(-), ez(-) | 0 | 0 | Pmax | 0 |
| ex(-), ez(+) | 0 | 0 | 0 | Pmax |
Zona D (zona de compressão trapezoidal)
A Zona D também corresponde a grandes excentricidades nas áreas ligadas na direção x da sapata, como mostrado na figura 4. A excentricidade na direção z (ez) é muito maior do que na direção x (ex). Nesse caso, dois cantos da sapata perdem contato com o solo e produzem uma área de compressão trapezoidal. Em comparação com a zona A, que está totalmente fora da zona secundária, uma parte da zona D ainda é coberta pela zona secundária.
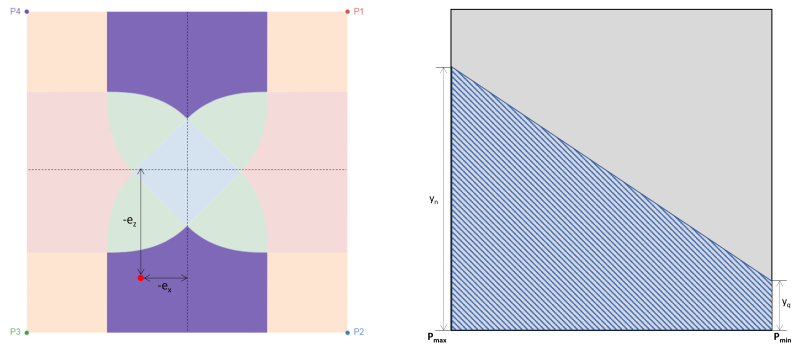
Figura 4: Excentricidade (-ex, -ez) na Zona D & área de compressão trapezoidal em torno de P3
Máximo & pressões de canto mínimas (lindo & Vestígio, 2017):
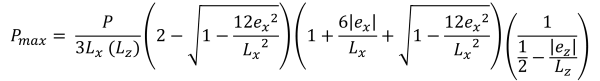
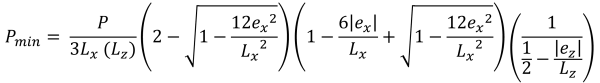
Alturas verticais da área compressiva trapezoidal (lindo & Vestígio, 2017):
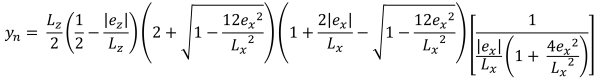
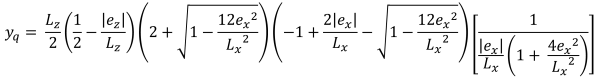
| Pressões de canto com base na excentricidade | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ex(+), ez(+) | Pmax | 0 | 0 | Pmin |
| ex(+), ez(-) | 0 | Pmax | Pmin | 0 |
| ex(-), ez(-) | 0 | Pmin | Pmax | 0 |
| ex(-), ez(+) | Pmin | 0 | 0 | Pmax |
Zona E (zona de compressão trapezoidal)
Semelhante à zona D, este caso também produz uma área compressiva trapezoidal, mas é causada por uma grande excentricidade na direção x(ex).
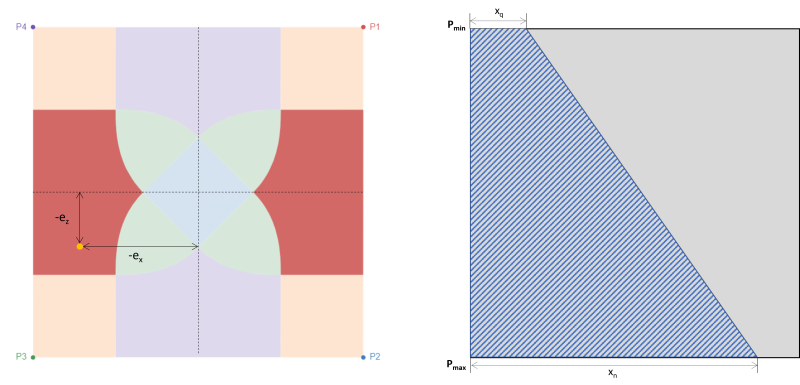Figura 5: Excentricidade (-ex, -ez) na Zona E & área de compressão trapezoidal em torno de P3
Máximo & pressões de canto mínimas (lindo & Vestígio, 2017):
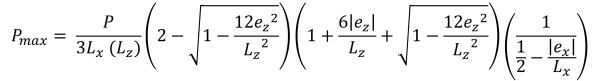
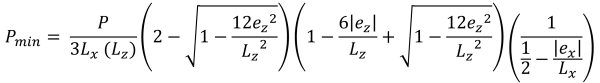
Bases horizontais da área compressiva trapezoidal (lindo & Vestígio, 2017):
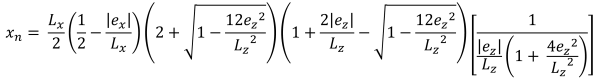
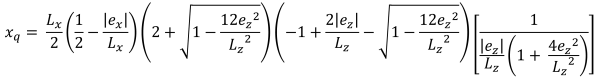
| Pressões de canto com base na excentricidade | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ex(+), ez(+) | Pmax | Pmin | 0 | 0 |
| ex(+), ez(-) | Pmin | Pmax | 0 | 0 |
| ex(-), ez(-) | 0 | 0 | Pmax | Pmin |
| ex(-), ez(+) | 0 | 0 | Pmin | Pmax |
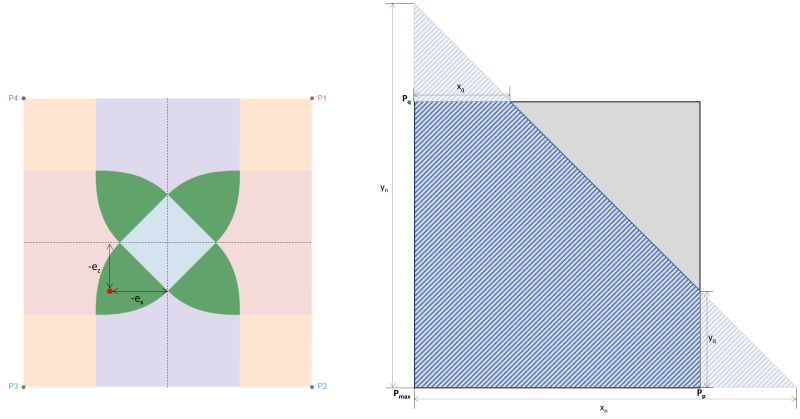
Zona B (Zona de compressão pentagonal)
Este caso ocorre quando as cargas aplicadas nas sapatas geram uma excentricidade moderada dentro da zona secundária. As áreas cobertas pela zona B são delimitadas por dois lados curvos e uma base plana em torno dos exteriores da zona C. Nesse caso, uma área compressiva pentagonal é produzida, e apenas um canto da sapata perde o contato com o solo. Contudo, as soluções fornecidas abaixo são ligeiramente complexas e requerem métodos de resolução numérica para as pressões de canto e o x & interceptações y da área compressiva.
Pressões de canto (lindo & Vestígio, 2017):
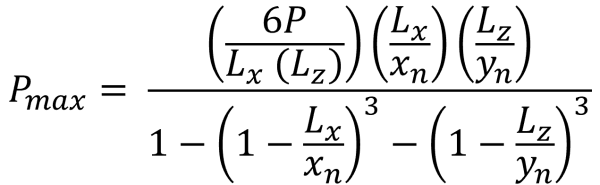
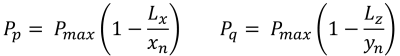
Lados pentagonais da área compressiva (lindo & Vestígio, 2017):
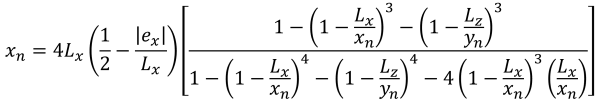
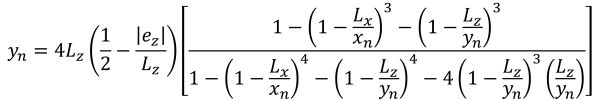
| Pressões de canto com base na excentricidade | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ex(+), ez(+) | Pmax | Pq | 0 | Pp |
| ex(+), ez(-) | Pp | Pmax | Pq | 0 |
| ex(-), ez(-) | 0 | Pp | Pmax | Pq |
| ex(-), ez(+) | Pq | 0 | Pp | Pmax |
Alternativamente, uma solução mais direta por S.S. Raio (1995) pode ser usado para as pressões de canto e interceptações da zona compressiva pentagonal. As equações são dadas abaixo:
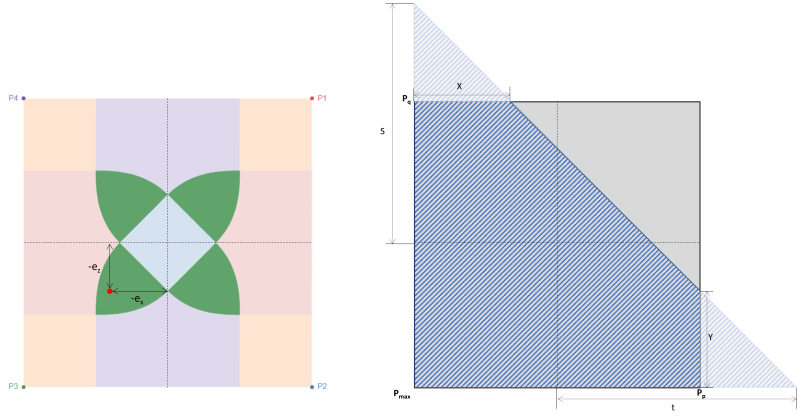
Pressões de canto (SS. Raio, 1995):
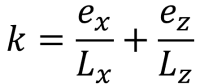
Lados pentagonais da área compressiva (SS. Raio, 1995):
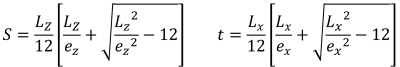
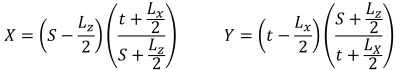
SkyCiv’s Módulo de Projeto de Fundação é capaz de resolver as pressões de base de uma sapata de concreto retangular. Verificações de projeto adicionais de acordo com diferentes códigos de projeto (ACI 318-14, padrão australiano 2009 & 2018, Eurocódigo, e padrões canadenses) também estão disponíveis.
Última atualização
A versão mais recente do módulo básico agora está integrada à Análise de Elementos Finitos (FEIO), que oferece uma análise de pressão do solo mais poderosa e introduz a análise de armação de madeira para ser usada para uma verificação de flexão muito mais detalhada. Os resultados FEA para a pressão do solo e momentos da armação da madeira podem ser visualizados em 3D e foram adicionados aos relatórios.
Quer experimentar o software de design de base da SkyCiv? Nossa ferramenta gratuita permite que os usuários realizem cálculos de base de concreto sem qualquer download ou instalação!
Referências:
- lindo, j., Vestígio, N. (2017). Solução Analítica Completa para Distribuição Linear da Pressão do Solo sob Sapatas Rígidas Retangulares.
- também é aplicável para calcular a capacidade de carga final de estacas em argila, Com base na Eq. (2007). também é aplicável para calcular a capacidade de carga final de estacas em argila (7ª edição). Com base na Eq
- Rawat, S., et. tudo. (2020). Sapatas retangulares isoladas sob flexão biaxial: Uma Avaliação Crítica e Metodologia de Análise Simplificada.
- Raio, SS. (1995). Concreto reforçado. Ciência Blackwell
Desenvolvedor de Produto
bacharelado (Civil), Mestrado (Civil)
