Exemplo de Design de Placa Base AISC Código Americano

Abaixo está um exemplo de alguns cálculos de placas de base americanas que são comumente usados ​​no projeto de placas de base. Design de placa de base de aço Eurocode, Design de placa de base de aço Eurocode, Design de placa de base de aço Eurocode:

• Design de placa de base de aço Eurocode – geralmente verificado em relação às forças de rolamento e compressão em referência ao ACI 318
• Design de placa de base de aço Eurocode – Design de placa de base de aço Eurocode, para garantir que eles forneçam contenção adequada e não falhem sob estresse para o AISC 360
• Design de placa de base de aço Eurocode – Design de placa de base de aço Eurocode, conforme mostrado abaixo nos cálculos de projeto do parafuso de ancoragem de exemplo para AISC
• Design de placa de base de aço Eurocode (Coluna) Verificações – Design de placa de base de aço Eurocode

Atualmente, a Design de placa de base de aço Eurocode Design de placa de base de aço Eurocode. Design de placa de base de aço Eurocode, inclui cálculos detalhados passo a passo, inclui cálculos detalhados passo a passo!

inclui cálculos detalhados passo a passo:

Calculadora de placas base

 

---

Carregar combinações:

A Design de placa de base de aço Eurocode o usa combinações de carga fatorada sob ASCE 7-10/16 aplica-se da seguinte forma:

1. \(1.4D )
2. \(1.2D + 1.6L + 0.5(EU_{r} \texto{ ou } S text{ ou } R)\)
3. \(1.2D + 1.6(Lr text{ ou } S text{ ou } R) + (L text{ ou } 0.5C)\)
4. \(1.2D + 1.0C + L + 0.5(Lr text{ ou } S text{ ou } R)\)
5. \(1.2D + 1.0E + L + 0.2S )
6. \(0.9D + 1.0C)
7. \(0.9D + 1.0E )

Onde :

\(D ) = carga morta
\(EU) = carga ao vivo
\(EU_{r}\) = carga viva do telhado
\(S ) = Carga de neve
\(R ) = Carga de chuva
\(E ) = Terremoto
\(C) = Carga de vento

inclui cálculos detalhados passo a passo:

Calculadora de placas base

 

---

Verificação do rolamento de concreto ACI:

A Design de placa de base de aço Eurocode verifica a resistência do rolamento de concreto (compressão) projeto de acordo com AISC 360-16 Eq. J8-2.

\( F_{b} = phi _{consequência} \vezes 0.85 \vezes f’_{c} \vezes A_{1} \times sqrt{ \fratura{ UMA_{2} }{ UMA_{1} } } \leq F_{b, limite} = 1.70 \vezes f’_{c} \vezes A_{1} \)

Onde:
\( f’_{c} \) - Resistência à compressão do concreto
\( UMA_{1} \) - área da placa de base em contato com a superfície de concreto
\( UMA_{2} \) - superfície de suporte de concreto
\( \phi_{consequência} \) – fator de resistência para concreto ( valor padrão = 0.65 )

inclui cálculos detalhados passo a passo:

Calculadora de placas base

 

---

Verificação do projeto de solda AISC:

A Design de placa de base de aço Eurocode verifica o projeto de solda de acordo com AISC 360-16 J2

\( (I) R_{n} = R_{nulo} + R_{nwt} \)

ou

\( (ii) R_{n} = 0,85R_{nulo} + 1.5R_{nwt} \)

Onde:

\(R_{nulo} \) = força nominal total de soldas de filete carregadas longitudinalmente.
\(R_{nwt} \) = força nominal total de soldas de filete carregadas transversalmente.

inclui cálculos detalhados passo a passo:

Calculadora de placas base

---

Verificação do projeto da âncora ACI:

A Design de placa de base de aço Eurocode verifica se os parâmetros de âncora se aplicam usando provisões de código da ACI 318-19 sob o capítulo 17.

As hastes de ancoragem são projetadas de acordo com AISC 360-16 - J9 e ACI 318-19 - Capítulo 17. As seguintes resistências de chumbadores são avaliadas:

• Resistência do aço da âncora em tensão e cisalhamento, \( \phi N_{para} \) e \( \phi V_{para} \).
• Resistência à ruptura do concreto na tração e cisalhamento, \( \phi N_{cbg} \) e \( \phi V_{cbg} \).
• Força de arrancamento de concreto, \( \phi N_{p} \).
• Resistência ao blowout da face lateral do concreto, \( \phi N_{sb} \).
• Resistência de remoção de concreto da âncora em cisalhamento, \( \phi V_{cp} \).

Resistência do aço da âncora em tensão e cisalhamento

Figura A. (uma) parafuso sem quebra (b) Quebra do parafuso devido a falha de tensão (c) Parafuso partido devido a falha de cisalhamento

A resistência do aço fatorada da âncora em tração e cisalhamento é determinada de acordo com ACI 318-19 - 17.6.1.2 e 17.7.1 como

Para Tensão

\( \phi _{tensão, anc} N_{para} = phi _{tensão, anc} UMA_{eu sei,N}f_{uta} \seta direita \) equação 17.6.1.2

Para cisalhamento

\( \phi _{o cisalhamento, anc} V_{para} = phi _{o cisalhamento, anc} 0.6UMA_{eu sei,V}f_{uta} \seta direita \) equação 17.7.1.2b

Onde:

• \( \phi _{tensão, anc} \) - fator de redução de força para âncoras em tensão ( valor padrão = 0.75 )
• \( \phi _{o cisalhamento, anc}\) - fator de redução de resistência para âncoras em cisalhamento ( valor padrão = 0.65 )
• \( UMA_{eu sei,N}\) - é a área da seção transversal efetiva de uma âncora em tensão.
• \( UMA_{eu sei,V}\) - é a área da seção transversal efetiva de uma âncora em cisalhamento.
• \( f_{uta}\) - resistência à tração especificada do aço de ancoragem e não deve ser maior que \(1.9f_{sim}\) e 125 ksi (861.845 Mpa)

Resistência à ruptura do concreto

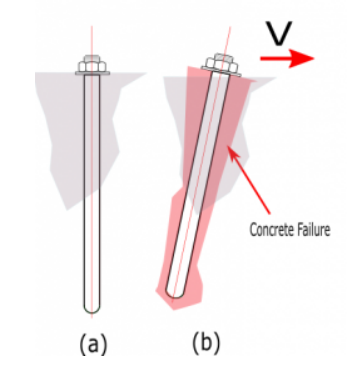
Figura B. (uma) Descanso do parafuso no concreto (b) rompimento do concreto devido à força de tração (c) rompimento do concreto devido à força de cisalhamento

 

A resistência à ruptura do concreto fatorada da âncora em tração e cisalhamento é determinada de acordo com o ACI 318-19 - 17.6.2 e 17.7.1 como

\( \phi N_{cbg} = phi frac{ UMA_{Nc} }{ UMA_{Lembrar} } \psi_{ec,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_{b} \seta direita \) equação 17.6.2.ab

Onde:

\( \phi \) – fator de redução de força para âncoras em tensão ( valor padrão = 0.75 ).
\( UMA_{Nc} \) – falha projetada de concreto de uma âncora única ou de grupo.
\( UMA_{Lembrar} \)- projetar área de falha de concreto de uma única âncora, para o cálculo da força na tensão, se não for limitada pela distância da borda ou espaçamento.

\( \psi_{ec,N} \) - Fator de excentricidade de ruptura na tensão.

\( \psi _{ec,N} = frac{1.00}{ 1 + \fratura{e ^{‘}_{N}}{1.5 h_{ef}} } \leq 1.00 \seta direita \) equação 17.6.2.3.1

\( \psi_{ed,N} \) - Fator de efeito de fuga na tensão.

(uma) \( \texto{E se } C_{uma,min} \geq 1.5h_{ef} \texto{ então } \psi _{ed,N} = 1.00 \) equação 17.6.2.4.1a

e

(b) \( \texto{E se } C_{uma,min} < 1.5h_{ef} \texto{ então } \psi _{ed,N} = 0.70 + 0.3\fratura{C_{uma,min}}{1.5h_{ef}} \) equação 17.6.2.4.1b

\( \psi_{c,N} \) - Fator de quebra de ruptura na tensão.

\( \psi _{c,N} = 1.25 \) para âncoras fundidas

\( \psi_{cp,N} \) - Fator de divisão de fuga na tensão.

(uma) \( \texto{E se } C_{uma,min} \geq C_{ac} \texto{ então } \psi _{cp,N} = 1.00 \) equação 17.6.2.4.1a

e

(b) \( \texto{E se } C_{uma,min} < C_{ac} \texto{ então } \psi _{cp,N} = frac{ C_{uma,min} }{ C_{ac}} \geq frac{ 1.5h_{ef} }{ C_{ac} } \) equação 17.6.2.4.1b

\( N_{b} \) – resistência básica à ruptura do concreto na tensão de uma única âncora em concreto rachado.

Força de arrancamento de concreto

Figura C. (uma) Descanso do parafuso no concreto (b) tração do parafuso do concreto devido à força de tração

 

A resistência ao arrancamento de concreto fatorada de uma âncora é definida no ACI 318-19 - 17.6.3 como

ϕN_pn = ϕΨ_c,P N_p

Onde:

\( \phi \) – fator de redução de força para âncoras em tensão ( valor padrão = 0.70 ).
\( \psi _{c, P} \) – fator de modificação para condição de concreto

Para concreto rachado:

\( \psi _{c, P} \) = 1.0

Para concreto não fissurado:

\( \psi _{c, P} \) = 1.4

\( N_{p} \) – Força de arrancamento da âncora

Para concreto rachado:

\( N_{p} = 8A_{brg}f ^{‘}_{c}\) equação 17.6.3.2.2a

Para concreto não fissurado:

\( N_{p} = 0.9f ^{‘}_{c}e_{h}d_{uma} \seta direita \) equação 17.6.2.2.b

Onde \( 3d_{uma} \leq e_{h} \leq 4.5d_{uma} \)

\( f ^{‘}_{c} \) – resistência à compressão especificada do concreto.
\( UMA_{brg} \) – área líquida de apoio da cabeça do prisioneiro, parafuso de ancoragem ou barra deformada com cabeça.
\( e_{h} \) – distância da superfície interna do eixo de um parafuso J ou L à ponta externa do J- ou L-bolt.
\( d_{uma} \) – diâmetro externo da âncora ou diâmetro do eixo do prisioneiro com cabeça, parafuso com cabeça, ou parafuso em forma de gancho.

Resistência ao blowout da face lateral do concreto

Figura D. (uma) Descanso do parafuso no concreto (b) parafuso com falha de concreto (Golpe lateral) próximo da borda à força de tensão

 

A resistência ao sopro da face lateral de concreto fatorada de uma âncora é definida no ACI 318-19 - 17.6.4 como

\( \phi N_{sb} = 160C_{a1}\sqrt{UMA_{brg}}\lambda _{uma} \sqrt{f ^{‘}_{c} } \seta direita \) equação 17.6.4.1

Onde:

\( f ^{‘}_{c} \) – resistência à compressão especificada do concreto.
\( UMA_{brg} \) – área líquida de apoio da cabeça do prisioneiro, parafuso de ancoragem ou barra deformada com cabeça.
\( \lambda_{uma} \) – fator de modificação para refletir as propriedades mecânicas reduzidas do concreto leve em certas aplicações de ancoragem de concreto.

Resistência concreta da âncora

\( \texto{V}_{ \texto{cp} } = text{k}_{cp} \times text{N}_{cp} \) 

ou 

\( \texto{V}_{ \texto{cpg} } = text{k}_{cpg} \times text{N}_{cpg} \)O blowout do concreto Pry-out é avaliado nas equações acima e os cálculos são baseados na resistência entre a haste de ancoragem e o concreto onde a instalação de falha usual da ancoragem pós-instalação, veja a Figura E abaixo.

Figuras E. (uma) Descanso do parafuso no concreto (b) parafuso com falha de concreto (Extrair) devido à força de cisalhamento. 

 

inclui cálculos detalhados passo a passo:

Calculadora de placas base