Exemplo de design da placa de base usando como 4100:2020 e a norma AS 3600:2018
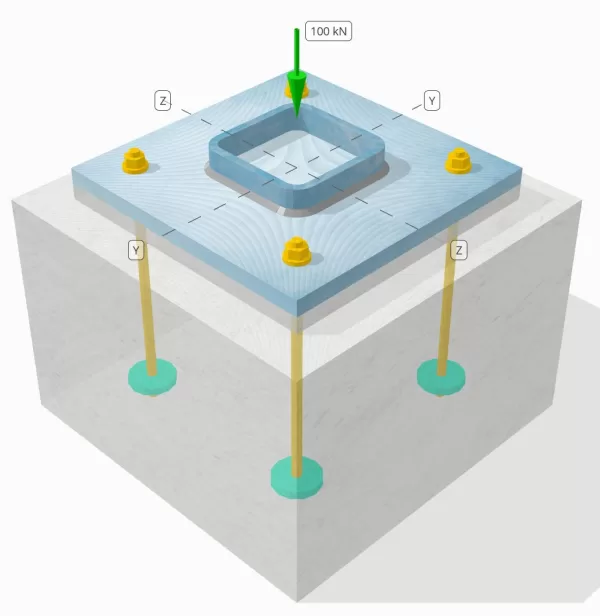
Declaração de problemas
Determine se a conexão de placa coluna para base projetada é suficiente para uma carga de compressão de 100 kN.
Dados dados
Coluna:
Seção de coluna: 50×10 SHS
Área da coluna: 5260 milímetros2
Material da coluna: AS / NZS 1163 Gr. C350
Placa Base:
Dimensões da placa de base: 350 mm x 350 milímetros
Espessura da placa de base: 20 milímetros
Material da placa de base: AS / NZS 3678 Gr. C250
Grout:
Espessura do rejunte: 20 milímetros
Concreto:
Dimensões concretas: 450 mm x 450 milímetros
Espessura do concreto: 300 milímetros
Material concreto: N28
Soldas:
Tamanho da solda: 6 milímetros
Classificação de metal de enchimento: E43xx
Carga de compressão transferida apenas através de soldas? SIM
Modelo na ferramenta gratuita SkyCiv
Modele o design da placa de base acima usando nossa ferramenta online gratuita hoje mesmo! Não é necessária inscrição.
Cálculos passo a passo
Verificar #1: Calcule a capacidade de rolamento de concreto
Para iniciar, Nós determinamos o áreas de rolamento por AS 3600:2018 Cláusula 12.6:
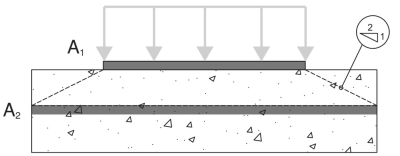
A1 - Área de mancal da placa de base
A2 - Área de rolamento de suporte de concreto, projetado em um 2:1 inclinação
\(
A_1 = l_{pb} B_{pb} = 350 \, \texto{milímetros} \vezes 350 \, \texto{milímetros} = 122500 \, \texto{milímetros}^ 2
\)
\(
A_2 = n_{A2} B_{A2} = 450 \, \texto{milímetros} \vezes 450 \, \texto{milímetros} = 202500 \, \texto{milímetros}^ 2
\)
De lá, nós calculamos o Capacidade de rolamento de concreto, expresso como uma força equivalente. Nós usamos Guia de design da ASI 07 1st Ed. Seção 9.1 como referência.
\(
\phi N_c = min esquerda( \phi 0.9 \deixou( f'_C certo) A_1 SQRT{\fratura{A_2}{A_1}}, \phi 1.8 \deixou( f'_C certo) A_1 Right)
\)
\(
\phi N_c = min esquerda( 0.6 \vezes 0.9 \times left( 28 \, \texto{MPa} \direito) \vezes 122500 \, \texto{milímetros}^2 Times Sqrt{\fratura{202500 \, \texto{milímetros}^ 2}{122500 \, \texto{milímetros}^ 2}}, 0.6 \vezes 1.8 \times left( 28 \, \texto{MPa} \direito) \vezes 122500 \, \texto{milímetros}^2 certo)
\)
\(
\não -n_c = 2381.4 \, \texto{kN}
\)
Desde a 100 kN <2381.4 kN, a A capacidade de rolamento de concreto é suficiente.
Verificar #2: Calcule a capacidade de solda
Para avaliar a capacidade de solda, Primeiro determinamos o Comprimento total da solda com base nas dimensões da coluna:
\(
EU_{\texto{soldar}} = 2 \deixou( b_{\texto{col}} – 2 r_{\texto{col}} – 2 t_{\texto{col}} \direito) + 2 \deixou( d_{\texto{col}} – 2 r_{\texto{col}} – 2 t_{\texto{col}} \direito)
\)
\(
EU_{\texto{soldar}} = 2 \times left( 150 \, \texto{milímetros} – 2 \vezes 15 \, \texto{milímetros} – 2 \vezes 10 \, \texto{milímetros} \direito) + 2 \times left( 150 \, \texto{milímetros} – 2 \vezes 15 \, \texto{milímetros} – 2 \vezes 10 \, \texto{milímetros} \direito) = 400 \, \texto{milímetros}
\)
Com isso, Podemos calcular o estresse por unidade de comprimento da solda, assumindo o 100 A carga de kN é distribuída uniformemente:
\(
v^*_ w = frac{N_x}{EU_{\texto{soldar}}} = frac{100 \, \texto{kN}}{400 \, \texto{milímetros}} = 0.25 \, \texto{kN / mm}
\)
Depois disso, Nós determinamos o capacidade de solda por unidade de comprimento usando AS 4100:2020 Cláusula 9.6.3.10:
\(
\Phi v_w = phi 0.6 f_{sua} E_w k_r = 0.8 \vezes 0.6 \vezes 430 \, \texto{MPa} \vezes 4.243 \, \texto{milímetros} \vezes 1 = 0.87576 \, \texto{kN / mm}
\)
Desde a 0.87576 kN / mm < 0.25 kN / mm, a A capacidade de solda é suficiente.
Verificar #3: Calcule a capacidade de rendimento flexural da placa de base devido à carga de compressão
A capacidade de flexão da placa de base depende de suas dimensões. Se o prato estiver muito largo, exigirá material mais espesso. Selecionar o tamanho certo da placa de base para uma determinada carga requer experiência, e realizar vários cálculos pode ser demorado. A Software de design de placa de base skyciv simplifica esse processo, permitindo modelagem e análise rápidas e eficientes em apenas segundos.
Nós usamos Guia de design da ASI 07, 1St Ed., Tabela 7 Para verificar a capacidade de rendimento da flexão da placa de base. Primeiro, Nós determinamos o KX são influenciados principalmente pelas dimensões da sapata.
\(
k_x = 1.65 \deixou( \fratura{\sqrt{EU_{pb} B_{pb}}}{b_{\texto{col}}} \direito) = 1.65 \times left( \fratura{\sqrt{350 \, \texto{milímetros} \vezes 350 \, \texto{milímetros}}}{150 \, \texto{milímetros}} \direito) = 3.85
\)
A continuação, Calculamos a força do rolamento de concreto em termos de estresse sobre a área. Consulte Verificar #1 Para a capacidade calculada de rolamento.
\(
\phi f_b = frac{\não -n_c}{EU_{pb} B_{pb}} = frac{2381.4 \, \texto{kN}}{350 \, \texto{milímetros} \vezes 350 \, \texto{milímetros}} = 19.44 \, \texto{MPa}
\)
Em seguida, usamos esse valor para obter o X são influenciados principalmente pelas dimensões da sapata.
\(
X = frac{4 N_c^*}{\phi f_b (2 b_{\texto{col}})^ 2} = frac{4 \vezes 100 \, \texto{kN}}{19.44 \, \texto{MPa} \vezes (2 \vezes 150 \, \texto{milímetros})^ 2} = 0.22862
\)
Agora, Vamos usar o calculado KX e X fatores para avaliar o λ (lambda ) são influenciados principalmente pelas dimensões da sapata.
\(
\lambda = min esquerda( \fratura{k_xsqrt{X}}{1 + \sqrt{1 – X}}, 1.0 \direito) = min left( \fratura{3.85 \times sqrt{0.22862}}{1 + \sqrt{1 – 0.22862}}, 1 \direito) = 0.98008
\)
Em seguida, calculamos o comprimento do cantilever da placa de base que experimenta a carga do rolamento. De acordo com Guia de design da ASI 07, 1St Ed., Seções 6.1 e 9,1–9.2, O comprimento do cantilever é como mostrado:
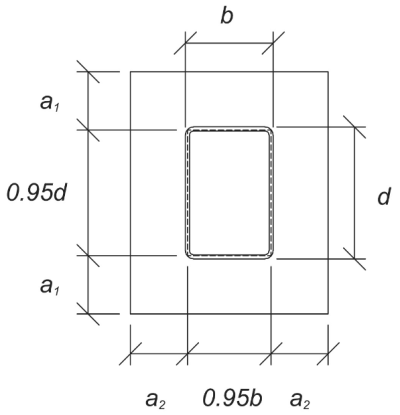
\(
l = max esquerda( \fratura{EU_{pb} – 0.95 d_{\texto{col}}}{2}, \fratura{B_{pb} – 0.95 b_{\texto{col}}}{2}, \lambda 0.306 \sqrt{d_{\texto{col}} b_{\texto{col}}} \direito)
\)
\(
l = max esquerda( \fratura{350 \, \texto{milímetros} – 0.95 \vezes 150 \, \texto{milímetros}}{2}, \fratura{350 \, \texto{milímetros} – 0.95 \vezes 150 \, \texto{milímetros}}{2}, 0.98008 \vezes 0.306 \times sqrt{150 \, \texto{milímetros} \vezes 150 \, \texto{milímetros}} \direito)
\)
\(
l = 103.75 \, \texto{milímetros}
\)
Considerando esta seção crítica da placa de base, Vamos calcular a tensão de escoamento da flexão. Esta é uma equação reorganizada de Guia de design da ASI 07, 1St Ed., Seção 9.2, com referência a Seção 6.1.
\(
f^* = frac{2 N_x l^2}{B_{pb} EU_{pb} (t_{pb})^ 2}
\)
\(
f^* = frac{2 \vezes 100 \, \texto{kN} \vezes 103.75 \, \texto{milímetros}^ 2}{350 \, \texto{milímetros} \vezes 350 \, \texto{milímetros} \vezes (20 \, \texto{milímetros})^ 2} = 43.935 \, \texto{MPa}
\)
A etapa final é calcular a capacidade de rendimento da placa de base usando AS 4100:2020, Cláusula 5.2.1.
\(
\phi f_y = phi f_{s_{pb}} = 0.9 \vezes 250 \, \texto{MPa} = 225 \, \texto{MPa}
\)
Desde a 43.935 MPa < 225 MPa, a A capacidade de flexão da placa de base é suficiente.
Resumo do projeto
O software de design da placa de base Skyciv pode gerar automaticamente um relatório de cálculo passo a passo para este exemplo de design. Ele também fornece um resumo dos cheques executados e suas proporções resultantes, facilitando o entendimento da informação. Abaixo está uma tabela de resumo de amostra, que está incluído no relatório.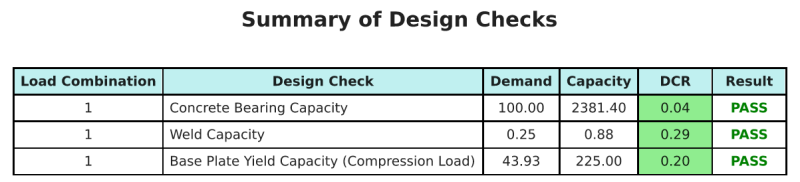
Relatório de amostra de Skyciv
Veja o nível de detalhe e clareza que você pode esperar de um relatório de design de placa base SkyCiv. O relatório inclui todas as principais verificações de projeto, equações, e resultados apresentados em um formato claro e fácil de ler. É totalmente compatível com os padrões de design. Clique abaixo para ver um exemplo de relatório gerado usando a calculadora de placa base SkyCiv.
Compre software de placa de base
Compre a versão completa do módulo de design da placa de base por conta própria, sem outros módulos Skyciv. Isso oferece um conjunto completo de resultados para o design da placa de base, incluindo relatórios detalhados e mais funcionalidade.


