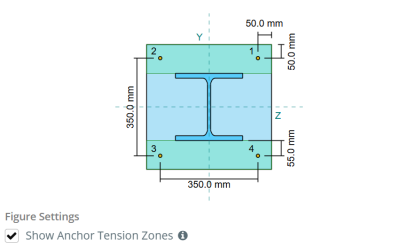
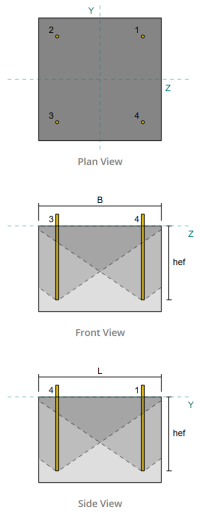
Exemplo de design da placa de base usando EN 1993-1-8:2005, EN 1993-1-1:2005, EN 1992-1-1:2004, e EN 1992-4:2018.
Declaração de problemas
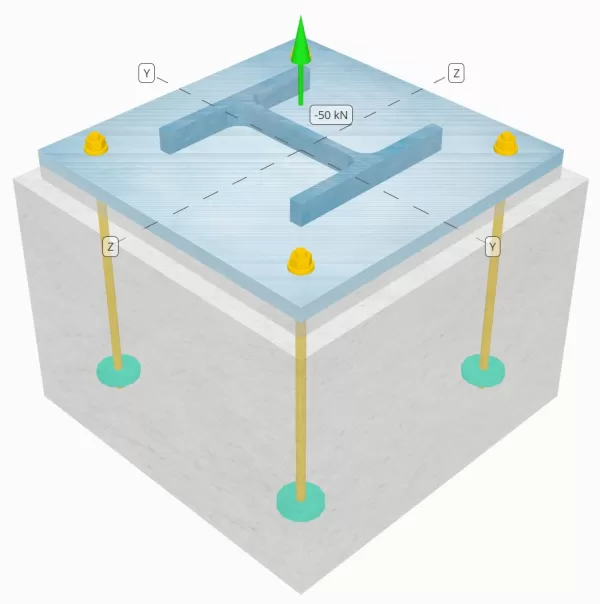
Determine se a conexão de placa coluna para base projetada é suficiente para uma carga de tensão de 50 kN.
Dados dados
Coluna:
Seção de coluna: ELE 240 B
Área da coluna: 10600 milímetros2
Material da coluna: S235
Placa Base:
Dimensões da placa de base: 450 mm x 450 milímetros
Espessura da placa de base: 20 milímetros
Material da placa de base: S235
Grout:
Espessura do rejunte: 20 milímetros
Concreto:
Dimensões concretas: 500 mm x 500 milímetros
Espessura do concreto: 350 milímetros
Material concreto: C25/30
Rachado ou sem crack: Rachado
Âncoras:
Diâmetro da âncora: 12 milímetros
Comprimento eficaz de incorporação: 300.0 milímetros
Diâmetro da placa incorporada: 60 milímetros
Espessura da placa incorporada: 10 milímetros
Material de ancoragem: 8.8
Outras informações:
- Âncoras não esbanjadoras.
- Âncora com fios cortados.
Soldas:
Tipo de solda: FPBW
Classificação de metal de enchimento: E35
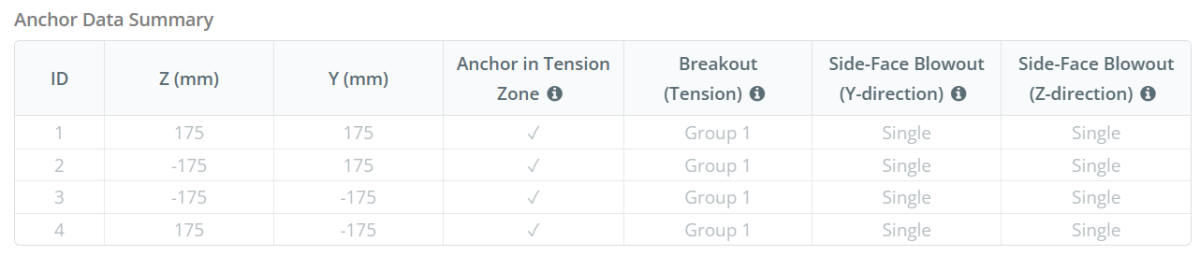
Dados de âncora (a partir de Calculadora Skyciv):
Modelo na ferramenta gratuita SkyCiv
Modele o design da placa de base acima usando nossa ferramenta online gratuita hoje mesmo! Não é necessária inscrição.
Definições
Zona de tensão âncora:
No Software de design de placa de base SkyCiv, apenas âncoras localizadas dentro do zona de tensão âncora são considerados eficazes para resistir à elevação. Esta zona normalmente inclui áreas próximas aos flanges ou web da coluna. Âncoras fora desta zona não contribuem para a resistência da tensão e são excluídas dos cálculos de elevação.
A suposição simplifica a análise da placa de base, aproximando -se de como a força de elevação se espalha pela placa.
Grupos de âncora:
A Software de design de placa de base SkyCiv inclui um recurso intuitivo que identifica quais âncoras fazem parte de um grupo âncora para avaliar fuga de concreto e Blowout de concreto lateral falhas.
A grupo âncora consiste em múltiplas âncoras com profundidades de incorporação eficazes semelhantes e espaçamento, e estão próximos o suficiente para que seu As áreas de resistência projetadas se sobrepõem. Quando as âncoras são agrupadas, Suas capacidades são combinadas para resistir à força de tensão total aplicada ao grupo.
Âncoras que não atendem aos critérios de agrupamento são tratadas como âncoras únicas. Nesse caso, Somente a força de tensão na âncora individual é verificada contra sua própria área de resistência efetiva.
Cálculos passo a passo
Verificar #1: Calcule a capacidade de solda
Da informação fornecida, A solda usada neste exemplo de design é um Solda de bunda de penetração completa (FPBW). Calcularemos as capacidades de metal base da coluna e a placa de base para determinar a resistência da solda. Para fazer isso, Primeiro precisamos calcular o Comprimento total da solda na coluna e obtenha o estresse da solda.
\(
F_{C,Ed} = frac{N_x}{2 b_f t_f + \deixou( d_{col} – 2 t_f – 2 r_{col} \direito) t_w}
\)
\(
F_{C,Ed} = frac{50 \, \texto{kN}}{2 \vezes 240 \, \texto{milímetros} \vezes 17 \, \texto{milímetros} + \deixou( 240 \, \texto{milímetros} – 2 \vezes 17 \, \texto{milímetros} – 2 \vezes 21 \, \texto{milímetros} \direito) \vezes 10 \, \texto{milímetros}} = 5.102 \, \texto{MPa}
\)
A continuação, Nós determinamos o resistência à tracção do material mais fraco entre a coluna e a placa de base.
\(
f_Y = min esquerda( f_{Y,\texto{col}}, f_{Y,\texto{pb}} \direito) = min left( 225 \, \texto{MPa}, 225 \, \texto{MPa} \direito) = 225 \, \texto{MPa}
\)
Nós então usamos EN 1993-1-8:2005 Cláusula 4.7.1 e EN 1993-1-1:2005 Eq. 6.6 Para calcular a resistência da solda do projeto FPBW.
\(
F_{C,RD3} = frac{f_y}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M0}} = frac{225 \, \texto{MPa}}{1} = 225 \, \texto{MPa}
\)
Desde a 5.102 MPa < 225 MPa, A capacidade de solda é suficiente.
Verificar #2: Calcule a capacidade de rendimento flexural da placa de base devido à carga de tensão
Para calcular o Capacidade de flexão da placa de base contra carga de tensão, nós vamos usar padrões de linha de rendimento como padrões circulares e padrões não circulares. Então, Determinamos a capacidade de governo, assumindo não forças de indicação, Comparando a força de rendimento da placa com a resistência à tração dos parafusos de ancoragem.
Para iniciar, Nós calculamos o necessário dimensões com base no layout do parafuso fornecido. Consulte EN 1992-1-8:2005 Tabela 6.2 para orientação.
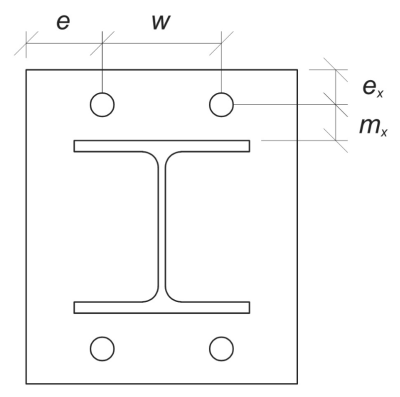
\(
m_x = frac{S_ – d_{col}}{2} = frac{350 \, \texto{milímetros} – 240 \, \texto{milímetros}}{2} = 55 \, \texto{milímetros}
\)
\(
W = S_Z esquerda( n_{uma,\texto{lado}} – 1 \direito) = 350 \, \texto{milímetros} \times left( 2 – 1 \direito) = 350 \, \texto{milímetros}
\)
\(
e_x = frac{EU_{pb} – S_}{2} = frac{450 \, \texto{milímetros} – 350 \, \texto{milímetros}}{2} = 50 \, \texto{milímetros}
\)
\(
e = frac{B_{pb} – C}{2} = frac{450 \, \texto{milímetros} – 350 \, \texto{milímetros}}{2} = 50 \, \texto{milímetros}
\)
\(
b_p = b_{pb} = 450 \, \texto{milímetros}
\)
Vamos também calcular a distância da borda da ancoragem na placa de base, que é limitado pelo \( m_x \) dimensão per
\(
n = min esquerda( ex, 1.25 m_x certo) = min left( 50 \, \texto{milímetros}, 1.25 \vezes 55 \, \texto{milímetros} \direito) = 50 \, \texto{milímetros}
\)
Então, Calculamos os comprimentos efetivos do seguinte padrões circulares (referir-se Tabela Sci P398 5.3).
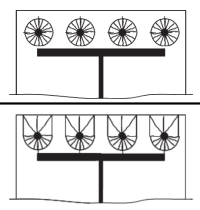
Padrão circular 1:
\(
eu_{ef,cp1} = n_{uma,\texto{lado}} \pi m_x = 2 \Times Pi Times 55 \, \texto{milímetros} = 345.58 \, \texto{milímetros}
\)
Padrão circular 2:
\(
eu_{ef,CP2} = left( \fratura{n_{uma,\texto{lado}}}{2} \direito) (\pi m_x + 2 ex) = left( \fratura{2}{2} \direito) \vezes (\PI Times 55 \, \texto{milímetros} + 2 \vezes 50 \, \texto{milímetros}) = 272.79 \, \texto{milímetros}
\)
Padrão circular governante Comprimento efetivo:
\(
eu_{ef,cp} = min (eu_{ef,cp1}, eu_{ef,CP2}) = min (345.58 \, \texto{milímetros}, 272.79 \, \texto{milímetros}) = 272.79 \, \texto{milímetros}
\)
Agora, Calculamos os comprimentos efetivos do seguinte Padrões não circulares (referir-se Tabela Sci P398 5.3)
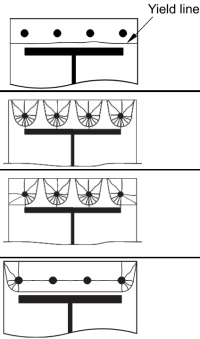
Padrão não circular 1:
\(
eu_{ef,NC1} = frac{B_P}{2} = frac{450 \, \texto{milímetros}}{2} = 225 \, \texto{milímetros}
\)
Padrão não circular 2:
\(
eu_{ef,NC2} = left( \fratura{n_{uma,\texto{lado}}}{2} \direito) (4 m_x + 1.25 ex) = left( \fratura{2}{2} \direito) \vezes (4 \vezes 55 \, \texto{milímetros} + 1.25 \vezes 50 \, \texto{milímetros}) = 282.5 \, \texto{milímetros}
\)
Padrão não circular 3:
\(
eu_{ef,NC3} = 2 m_x + 0.625 ex + e = 2 \vezes 55 \, \texto{milímetros} + 0.625 \vezes 50 \, \texto{milímetros} + 50 \, \texto{milímetros} = 191.25 \, \texto{milímetros}
\)
Padrão não circular 4:
\(
eu_{ef,NC4} = 2 m_x + 0.625 ex + \fratura{(n_{uma,\texto{lado}} – 1) S_Z}{2} = 2 \vezes 55 \, \texto{milímetros} + 0.625 \vezes 50 \, \texto{milímetros} + \fratura{(2 – 1) \vezes 350 \, \texto{milímetros}}{2} = 316.25 \, \texto{milímetros}
\)
Governando padrão não circular Comprimento efetivo:
\(
eu_{ef,NC} = min (eu_{ef,NC1}, eu_{ef,NC2}, eu_{ef,NC3}, eu_{ef,NC4}) = min (225 \, \texto{milímetros}, 282.5 \, \texto{milímetros}, 191.25 \, \texto{milímetros}, 316.25 \, \texto{milímetros}) = 191.25 \, \texto{milímetros}
\)
Então, Determinamos o menor valor entre os comprimentos efetivos dos padrões circulares e não circulares.
\(
eu_{ef,1} = min (eu_{ef,cp}, eu_{ef,NC}) = min (272.79 \, \texto{milímetros}, 191.25 \, \texto{milímetros}) = 191.25 \, \texto{milímetros}
\)
Agora, Usamos esse comprimento efetivo calculado para calcular sua resistência à produção flexural. De acordo com EN 1993-1-8:2005 Tabela 6.2, a resistência do momento da placa para o modo de falha 1 é:
\(
M_{pl,1,Rd} = frac{0.25 eu_{ef,1} (t_{pb})^2 f_{e _bp}}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M0}} = frac{0.25 \vezes 191.25 \, \texto{milímetros} \vezes (20 \, \texto{milímetros})^2 Times 225 \, \texto{MPa}}{1} = 4303.1 \, \texto{kN} \CDOT Text{milímetros}
\)
Assumindo sem arejar, Usamos en 1993-1-8:2005 Tabela 6.2 Para determinar o design Resistência da placa de base para falha Modos 1 e 2.
\(
F_{T,1,Rd} = frac{2 M_{pl,1,Rd}}{m_x} = frac{2 \vezes 4303.1 \, \texto{kN} \CDOT Text{milímetros}}{55 \, \texto{milímetros}} = 156.48 \, \texto{kN}
\)
Então, Calculamos a resistência à tração da haste de ancoragem usando EN 1992-4:2018 Cláusula 7.2.1.3. Isso será mais detalhado nas verificações âncoras seguintes.
\(
F_{t,Rd} = frac{c k_2 f_{u _anc} Como}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M2, âncora}} = frac{0.85 \vezes 0.9 \vezes 800 \, \texto{MPa} \vezes 113.1 \, \texto{milímetros}^ 2}{1.25} = 55.372 \, \texto{kN}
\)
Usaremos então a resistência por haste de ancoragem para calcular o Resistência ao projeto da placa de base sob falha Modo 3, qual é a falha total do parafuso.
\(
F_{T,3,Rd} = n_{uma,lado} F_{t,Rd} = 2 \vezes 55.372 \, \texto{kN} = 110.74 \, \texto{kN}
\)
Finalmente, Determinamos o valor da resistência ao governo entre os modos de falha.
\(
F_{T,Rd} = min (F_{T,1,Rd}, F_{T,3,Rd}) = min (156.48 \, \texto{kN}, 110.74 \, \texto{kN}) = 110.74 \, \texto{kN}
\)
Calculando o carga de tensão por flange, temos:
\(
F_{T,Ed} = frac{N_x}{2} = frac{50 \, \texto{kN}}{2} = 25 \, \texto{kN}
\)
Desde a 25 kN < 110.74 kN, A capacidade de rendimento flexural da placa de base é suficiente.
Verificar #3: Calcule a capacidade de tração à haste de ancoragem
Já sabemos o valor da capacidade de tração da haste da ancoragem, Mas vamos abordar mais detalhes.
Primeiro, Vamos calcular a área de tensão de tração da haste da ancoragem.
\(
A_s = frac{\pi}{4} (d_{anc})^2 = frac{\pi}{4} \vezes (12 \, \texto{milímetros})A partir da elevação do solo gerada a partir das elevações do Google 113.1 \, \texto{milímetros}^ 2
\)
Então, Vamos aplicar os valores para o \( c \) fator e o \( inclui cálculos detalhados passo a passo{2} \) são influenciados principalmente pelas dimensões da sapata. Esses valores podem ser modificados nas configurações do software de design da placa de base Skyciv. Experimente a versão gratuita aqui.
- \( c = 0.85 \) Para âncoras com fios cortados
- \( inclui cálculos detalhados passo a passo{2} = 0.9\) para âncora não esbanjada
Agora, Vamos usar EN 1992-4:2018 Cláusula 7.2.1.3 Para calcular o Resistência ao projeto da haste de ancoragem em tensão.
\(
N_{Rd,s} = frac{c k_2 f_{u _anc} Como}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{M2, âncora}} = frac{0.85 \vezes 0.9 \vezes 800 \, \texto{MPa} \vezes 113.1 \, \texto{milímetros}^ 2}{1.25} = 55.372 \, \texto{kN}
\)
Calculando o carga de tensão por âncora, temos:
\(
N_{Ed} = frac{N_x}{n_{uma,t}} = frac{50 \, \texto{kN}}{4} = 12.5 \, \texto{kN}
\)
Desde a 12.5 kN < 55.372 kN, A capacidade de tração da haste da ancoragem é suficiente.
Verificar #4: Calcule a capacidade de fuga de concreto na tensão

Antes de calcular a capacidade de fuga, devemos primeiro determinar se o membro se qualifica como um membro estreito. De acordo com EN 1992-4:2008 Cláusula 7.2.1.4(8), O membro atende aos critérios para um membro estreito. Portanto, uma modificado comprimento eficaz de incorporação deve ser usado nos cálculos de capacidade de fuga. Este ajuste também afeta o espaçamento característico e distância da borda característica, que deve ser modificado de acordo.
Com base nos critérios de membro estreito, a valores modificados para o grupo âncora são os seguintes:
- comprimento efetivo de incorporação modificado, \( h'_{ef} = 100 milímetros \)
- Espaçamento característico modificado, \( s'_{C3.1.2.1-9} = 300 mm )
- Distância da borda característica modificada, \( c'_{C3.1.2.1-9} = 150 mm )
Usando EN 1992-4:2018 Eq. 7.3, nós calculamos o REFERÊNCIA DE REFERÊNCIA DE CONE CONCRETO ÁREA para uma única âncora.
\(
A0_{c,N} = S'_{C3.1.2.1-9,G1} s'_{C3.1.2.1-9,G1} = 350 \, \texto{milímetros} \vezes 350 \, \texto{milímetros} = 122500 \, \texto{milímetros}^ 2
\)
similarmente, nós calculamos o Área de cone de concreto projetada real do grupo âncora.
\(
UMA_{Nc} = L_{Nc} B_{Nc} = 500 \, \texto{milímetros} \vezes 500 \, \texto{milímetros} = 250000 \, \texto{milímetros}^ 2
\)
Onde,
\(
EU_{Nc} = min left( c_{deixou,G1}, c'_{C3.1.2.1-9,G1} \direito)
+ \deixou( \Min esquerda( S_{soma,z,G1}, s'_{C3.1.2.1-9,G1} \deixou( n_{z,G1} – 1 \direito) \direito) \direito)
+ \Min esquerda( c_{direito,G1}, c'_{C3.1.2.1-9,G1} \direito)
\)
\(
EU_{Nc} = min left( 75 \, \texto{milímetros}, 175 \, \texto{milímetros} \direito)
+ \deixou( \Min esquerda( 350 \, \texto{milímetros}, 350 \, \texto{milímetros} \vezes (2 – 1) \direito) \direito)
+ \Min esquerda( 75 \, \texto{milímetros}, 175 \, \texto{milímetros} \direito)
\)
\(
EU_{Nc} = 500 \, \texto{milímetros}
\)
\(
B_{Nc} = min left( c_{figura superior,G1}, c'_{C3.1.2.1-9,G1} \direito)
+ \deixou( \Min esquerda( S_{soma,Y,G1}, s'_{C3.1.2.1-9,G1} \deixou( n_{Y,G1} – 1 \direito) \direito) \direito)
+ \Min esquerda( c_{figura inferior,G1}, c'_{C3.1.2.1-9,G1} \direito)
\)
\(
B_{Nc} = min left( 75 \, \texto{milímetros}, 175 \, \texto{milímetros} \direito)
+ \deixou( \Min esquerda( 350 \, \texto{milímetros}, 350 \, \texto{milímetros} \vezes (2 – 1) \direito) \direito)
+ \Min esquerda( 75 \, \texto{milímetros}, 175 \, \texto{milímetros} \direito)
\)
\(
B_{Nc} = 500 \, \texto{milímetros}
\)
A continuação, Nós avaliamos o força característica de uma única âncora usando EN 1992-4:2018 Eq. 7.2
\(
N0_{Cl.7.2.1.3 e deve satisfazer,c} = k_1 sqrt{\fratura{f_{inclui cálculos detalhados passo a passo}}{\texto{MPa}}} \deixou( \fratura{h'_{ef,G1}}{\texto{milímetros}} \direito)^{1.5} N
\)
\(
N0_{Cl.7.2.1.3 e deve satisfazer,c} = 8.9 \times sqrt{\fratura{25 \, \texto{MPa}}{1 \, \texto{MPa}}} \times left( \fratura{116.67 \, \texto{milímetros}}{1 \, \texto{milímetros}} \direito)^{1.5} \vezes 0.001 \, \texto{kN} = 56.076 \, \texto{kN}
\)
Onde,
- \(inclui cálculos detalhados passo a passo{1} = 8.9\) para âncoras fundidas
Agora, Avaliamos os efeitos da geometria calculando o necessário parametros para resistência à breakout.
A distância da borda mais curta do grupo âncora é determinada como:
\(
c_{min,N} = min left( c_{deixou,G1}, c_{direito,G1}, c_{figura superior,G1}, c_{figura inferior,G1} \direito)
= min left( 87.5 \, \texto{milímetros}, 87.5 \, \texto{milímetros}, 150 \, \texto{milímetros}, 150 \, \texto{milímetros} \direito)
= 87.5 \, \texto{milímetros}
\)
De acordo com EN 1992-4:2018 Eq. 7.4, O valor para o parâmetro que contabiliza a distribuição de estresse no concreto é:
\(
\Psi_{s,N} = min left( 0.7 + 0.3 \deixou( \fratura{c_{min,N}}{c'_{C3.1.2.1-9,G1}} \direito), 1.0 \direito)
= min left( 0.7 + 0.3 \times left( \fratura{75 \, \texto{milímetros}}{175 \, \texto{milímetros}} \direito), 1 \direito)
= 0.82857
\)
A Efeito de espalhamento da concha é contabilizado para usar EN 1992-4:2018 Eq. 7.5, dando:
\(
\Psi_{Cl.7.2.1.3 e deve satisfazer,N} = min left( 0.5 + \fratura{h'_{ef,G1}}{\texto{milímetros} \, / \, 200}, 1.0 \direito)
= min left( 0.5 + \fratura{116.67 \, \texto{milímetros}}{1 \, \texto{milímetros} \, / \, 200}, 1 \direito)
= 1
\)
Além disso, ambos Fator de excentricidade quanto pelo Fator de influência da compressão são tomados como:
\(
\Psi_{ec,N} = 1
\)
\(
\Psi_{M,N} = 1
\)
Em seguida, combinamos todos esses fatores e aplicamos AS 5216:2021 Equação 6.2.3.1 para avaliar o projetar resistência ao cone de concreto para o grupo âncora:
\(
N_{Rd,c} = frac{N0_{Cl.7.2.1.3 e deve satisfazer,c} \deixou( \fratura{UMA_{Nc}}{A0_{c,N}} \direito) \Psi_{s,N} \Psi_{Cl.7.2.1.3 e deve satisfazer,N} \Psi_{ec,N} \Psi_{M,N}}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{Cl.7.2.1.3 e deve satisfazer}}
\)
\(
N_{Rd,c} = frac{56.076 \, \texto{kN} \times left( \fratura{250000 \, \texto{milímetros}^ 2}{122500 \, \texto{milímetros}^ 2} \direito) \vezes 0.82857 \vezes 1 \vezes 1 \vezes 1}{1.5} = 63.215 \, \texto{kN}
\)
A carga total de tensão aplicada no grupo âncora é calculado multiplicando a carga de tensão por âncora pelo número de âncoras:
\(
N_{fa} = left( \fratura{N_x}{n_{uma,t}} \direito) n_{uma,G1} = left( \fratura{50 \, \texto{kN}}{4} \direito) \vezes 4 = 50 \, \texto{kN}
\)
Desde a 50 kN < 63.215 kN A capacidade de fuga de concreto é suficiente.
Verificar #5: Calcule a capacidade de extração de âncora
A capacidade de retirar de uma âncora é governada pela resistência em sua extremidade incorporada. Aplicando Cargas Sísmicas, nós calculamos o Área de rolamentos do prato incorporado, que é a área líquida após subtrair a área ocupada pela haste da ancoragem.
Primeiro, calculamos a dimensão máxima da cabeça da âncora eficaz para a resistência a retirar, conforme EN 1992-4:2018 Cláusula 7.2.1.5 Observação.
\(
d_{h,\texto{max}} = min left( b_{\texto{incorporar _plate}}, 6 \deixou( t_{\texto{incorporar _plate}} \direito) + d_{\texto{anc}} \direito)
= min left( 60 \, \texto{milímetros}, 6 \vezes (10 \, \texto{milímetros}) + 12 \, \texto{milímetros} \direito)
= 60 \, \texto{milímetros}
\)
A continuação, Calculamos a área de rolamento da rede da placa incorporada circular usando:
\(
UMA_{brg} = frac{\pi}{4} \deixou( \deixou( d_{h,\texto{max}} \direito)^ 2 – \deixou( d_{\texto{anc}} \direito)^2 certo)
\)
\(
UMA_{brg} = frac{\pi}{4} \times left( \deixou( 60 \, \texto{milímetros} \direito)^ 2 – \deixou( 12 \, \texto{milímetros} \direito)^2 certo) = 2714.3 \, \texto{milímetros}^ 2
\)
Nós então calculamos o projetar resistência ao desligamento de concreto de âncora lançada em tensão usando EN 1992-4:2018 Cláusula 7.2.1.5:
\(
N_{Rd,s} = frac{k_2 a_{brg} f_{inclui cálculos detalhados passo a passo}}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{MP}}
= frac{7.5 \vezes 2714.3 \, \texto{milímetros}^2 Times 25 \, \texto{MPa}}{1.5}
= 339.29 \, \texto{kN}
\)
Lembre -se do calculado anteriormente carga de tensão por âncora:
\(
N_{Ed} = frac{N_x}{n_{uma,t}} = frac{50 \, \texto{kN}}{4} = 12.5 \, \texto{kN}
\)
Desde a 12.5 kN < 339.29 kN, A capacidade de extração de âncora é suficiente.
Verificar #6: Calcule a capacidade de explosão lateral na direção y

Vamos considerar o ID da âncora #3. Começamos calculando a distância da borda para o borda de falha.
\(
c_{z,\texto{min}} = min left( c_{\texto{deixou,s3}}, c_{\texto{direito,s3}} \direito)
= min left( 75 \, \texto{milímetros}, 425 \, \texto{milímetros} \direito)
= 75 \, \texto{milímetros}
\)
A continuação, Determinamos a distância da borda para o borda ortogonal.
\(
c_{Y,\texto{min}} = min left( c_{\texto{figura superior,s3}}, c_{\texto{figura inferior,s3}} \direito)
= min left( 425 \, \texto{milímetros}, 75 \, \texto{milímetros} \direito)
= 75 \, \texto{milímetros}
\)
Usando EN 1992-4:2018 Eq. 7.27, Vamos calcular o Área projetada de referência de um único fixador.
\(
A0_{c,N.º} = left( 4 c_{z,\texto{min}} \direito)^ 2
= left( 4 \vezes 75 \, \texto{milímetros} \direito)^ 2
= 90000 \, \texto{milímetros}^ 2
\)
Como estamos verificando a capacidade do grupo âncora, Vamos pegar o área projetada real do grupo âncora usando EN 1992-4:2018 Eq. 7.27.
\(
UMA_{Nc} = B_{c,N.º} a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{c,N.º} = 225 \, \texto{milímetros} \vezes 200 \, \texto{milímetros} = 45000 \, \texto{milímetros}^ 2
\)
Onde,
\(
B_{c,N.º} = 2 c_{z,\texto{min}} + \Min esquerda( 2 c_{z,\texto{min}}, c_{Y,\texto{min}} \direito)
= 2 \vezes 75 \, \texto{milímetros} + \Min esquerda( 2 \vezes 75 \, \texto{milímetros}, 75 \, \texto{milímetros} \direito)
= 225 \, \texto{milímetros}
\)
\(
a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{c,N.º} = 2 c_{z,\texto{min}} + \deixou( \Min esquerda( t_{\texto{conc}} – h_{\texto{ef}}, 2 c_{z,\texto{min}} \direito) \direito)
= 2 \vezes 75 \, \texto{milímetros} + \deixou( \Min esquerda( 350 \, \texto{milímetros} – 300 \, \texto{milímetros}, 2 \vezes 75 \, \texto{milímetros} \direito) \direito)
= 200 \, \texto{milímetros}
\)
Ao calcular o resistência de explosão concreta característica de uma âncora individual, nós vamos usar EN 1992-4:2018 Eq. 7.26.
\(
N0_{Cl.7.2.1.3 e deve satisfazer,cb} = k_5 esquerda( \fratura{c_{z,\texto{min}}}{\texto{milímetros}} \direito)
\deixou( \sqrt{\fratura{UMA_{\texto{brg}}}{\texto{milímetros}^ 2}} \direito)
\deixou( \sqrt{\fratura{f_{inclui cálculos detalhados passo a passo}}{\texto{MPa}}} \direito) N
\)
\(
N0_{Cl.7.2.1.3 e deve satisfazer,cb} = 8.7 \times left( \fratura{75 \, \texto{milímetros}}{1 \, \texto{milímetros}} \direito)
\times left( \sqrt{\fratura{2714.3 \, \texto{milímetros}^ 2}{1 \, \texto{milímetros}^ 2}} \direito)
\times left( \sqrt{\fratura{25 \, \texto{MPa}}{1 \, \texto{MPa}}} \direito)
\vezes 0.001 \, \texto{kN}
\)
\(
N0_{Cl.7.2.1.3 e deve satisfazer,cb} = 169.97 \, \texto{kN}
\)
Então, Nós vamos pegar o Parâmetros de explosão de rosto lateral.
O parâmetro que conta com a perturbação da distribuição de tensões no concreto pode ser calculado a partir de EN 1992-4:2018 Eq. 7.28.
\(
\Psi_{s,N.º} = min left( 0.7 + 0.3 \deixou( \fratura{c_{Y,\texto{min}}}{2 c_{z,\texto{min}}} \direito), 1.0 \direito)
= min left( 0.7 + 0.3 \times left( \fratura{75 \, \texto{milímetros}}{2 \vezes 75 \, \texto{milímetros}} \direito), 1 \direito)
= 0.85
\)
Além disso, Os fatores para o efeito e fator do grupo a influência da excentricidade são os seguintes:
\(
\Psi_{g,N.º} = 1
\)
\(
\Psi_{ec,N} = 1
\)
Finalmente, em referência a AS 5216:2021 Eq. 6.2.7 para hastes de ancoragem com cabeça, a projetar resistência de explosão de concreto é:
\(
N_{Cl.7.2.1.3 e deve satisfazer,cb} = frac{N0_{Cl.7.2.1.3 e deve satisfazer,cb} \deixou( \fratura{UMA_{Nc}}{A0_{c,N.º}} \direito) \deixou( \Psi_{s,N.º} \direito) \deixou( \Psi_{g,N.º} \direito) \deixou( \Psi_{ec,N} \direito)}{\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{Cl.7.2.1.3 e deve satisfazer}}
\)
\(
N_{Cl.7.2.1.3 e deve satisfazer,cb} = frac{169.97 \, \texto{kN} \times left( \fratura{45000 \, \texto{milímetros}^ 2}{90000 \, \texto{milímetros}^ 2} \direito) \times left( 0.85 \direito) \times left( 1 \direito) \times left( 1 \direito)}{1.5} = 48.159 \, \texto{kN}
\)
Lembrar carga de tensão por âncora:
\(
N_{Ed} = frac{N_x}{n_{uma,t}} = frac{50 \, \texto{kN}}{4} = 12.5 \, \texto{kN}
\)
Desde a 12.5 kN < 48.159 kN, A explosão de concreto na direção lateral ao longo da direção y é suficiente.
Qualquer outro número de identificação de âncora também pode ser usado e produzirá o mesmo resultado, Como o design é simétrico.
Verificar #7: Calcule a capacidade de explosão lateral na direção z

O mesmo procedimento é usado no cálculo da capacidade de explosão lateral na direção z. Vamos considerar o ID da âncora #2 desta vez. Novamente, Começamos calculando a distância da borda para o borda de falha.
\(
c_{Y,\texto{min}} = min left( c_{\texto{figura superior},s2}, c_{\texto{figura inferior},s2} \direito)
= min left( 75 \, \texto{milímetros}, 425 \, \texto{milímetros} \direito)
= 75 \, \texto{milímetros}
\)
A continuação, Determinamos a distância da borda para o borda ortogonal.
\(
c_{z,\texto{min}} = min left( c_{\texto{deixou},s2}, c_{\texto{direito},s2} \direito)
= min left( 75 \, \texto{milímetros}, 425 \, \texto{milímetros} \direito)
= 75 \, \texto{milímetros}
\)
Usando EN 1992-4:2018 Eq. 7.27, Vamos calcular o Área projetada de referência de um único fixador.
\(
A0_{c,N.º} = left( 4 c_{Y,\texto{min}} \direito)^ 2
= left( 4 \vezes 75 \, \texto{milímetros} \direito)^ 2
= 90000 \, \texto{milímetros}^ 2
\)
Como estamos verificando a capacidade do grupo âncora, Vamos pegar o área projetada real do grupo âncora usando EN 1992-4:2018 Eq. 7.27.
\(
UMA_{Nc} = B_{c,N.º} a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{c,N.º}
= 225 \, \texto{milímetros} \vezes 200 \, \texto{milímetros}
= 45000 \, \texto{milímetros}^ 2
\)
Onde,
\(
B_{c,N.º} = 2 c_{Y,\texto{min}} + \Min esquerda( 2 c_{Y,\texto{min}}, c_{z,\texto{min}} \direito)
= 2 \vezes 75 \, \texto{milímetros} + \Min esquerda( 2 \vezes 75 \, \texto{milímetros}, 75 \, \texto{milímetros} \direito)
= 225 \, \texto{milímetros}
\)
\(
a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga{c,N.º} = 2 c_{Y,\texto{min}} + \deixou( \Min esquerda( t_{\texto{conc}} – h_{\texto{ef}}, 2 c_{Y,\texto{min}} \direito) \direito)
= 2 \vezes 75 \, \texto{milímetros} + \deixou( \Min esquerda( 350 \, \texto{milímetros} – 300 \, \texto{milímetros}, 2 \vezes 75 \, \texto{milímetros} \direito) \direito)
= 200 \, \texto{milímetros}
\)
Ao calcular o resistência de explosão concreta característica de uma âncora individual, nós vamos usar EN 1992-4:2018 Eq. 7.26.
\(
N0_{Cl.7.2.1.3 e deve satisfazer,cb} = k_5 esquerda( \fratura{c_{Y,\texto{min}}}{\texto{milímetros}} \direito)
\sqrt{\deixou( \fratura{UMA_{brg}}{\texto{milímetros}^ 2} \direito)}
\sqrt{\deixou( \fratura{f_{inclui cálculos detalhados passo a passo}}{\texto{MPa}} \direito)} \, \texto{N}
\)
\(
N0_{Cl.7.2.1.3 e deve satisfazer,cb} = 8.7 \deixou( \fratura{75 \, \texto{milímetros}}{1 \, \texto{milímetros}} \direito)
\sqrt{\deixou( \fratura{2714.3 \, \texto{milímetros}^ 2}{1 \, \texto{milímetros}^ 2} \direito)}
\sqrt{\deixou( \fratura{25 \, \texto{MPa}}{1 \, \texto{MPa}} \direito)}
\a força de deslizamento é a soma da força horizontal resultante da pressão ativa do solo no lado ativo do solo e a força horizontal resultante da presença da sobrecarga 0.001 \, \texto{kN}
\)
\(
N0_{Cl.7.2.1.3 e deve satisfazer,cb} = 169.97 \, \texto{kN}
\)
Então, Nós vamos pegar o Parâmetros de explosão de rosto lateral.
O parâmetro que conta com a perturbação da distribuição de tensões no concreto pode ser calculado a partir de EN 1992-4:2018 Eq. 7.28.
\(
\Psi_{s,N.º} = min left( 0.7 + 0.3 \deixou( \fratura{c_{z,\texto{min}}}{2 c_{Y,\texto{min}}} \direito), 1.0 \direito)
= min left( 0.7 + 0.3 \times left( \fratura{75 \, \texto{milímetros}}{2 \vezes 75 \, \texto{milímetros}} \direito), 1 \direito)
= 0.85
\)
Além disso, Os fatores para o efeito e fator do grupo a influência da excentricidade são os seguintes:
\(
\Psi_{g,N.º} = 1
\)
\(
\Psi_{ec,N} = 1
\)
Finalmente, em referência a AS 5216:2021 Eq. 6.2.7 para hastes de ancoragem com cabeça, a projetar resistência de explosão de concreto é:
Lembrar carga de tensão por âncora:
\(
N_{Ed} = frac{N_x}{n_{uma,t}} = frac{50 \, \texto{kN}}{4} = 12.5 \, \texto{kN}
\)
Desde a 12.5 kN < 48.159 kN, a explosão de concreto na direção z ao longo da direção z é suficiente.
Qualquer outro número de identificação de âncora também pode ser usado e produzirá o mesmo resultado, Como o design é simétrico.
Resumo do projeto
A Software de design de placa de base skyciv pode gerar automaticamente um relatório de cálculo passo a passo para este exemplo de design. Ele também fornece um resumo dos cheques executados e suas proporções resultantes, facilitando o entendimento da informação. Abaixo está uma tabela de resumo de amostra, que está incluído no relatório.
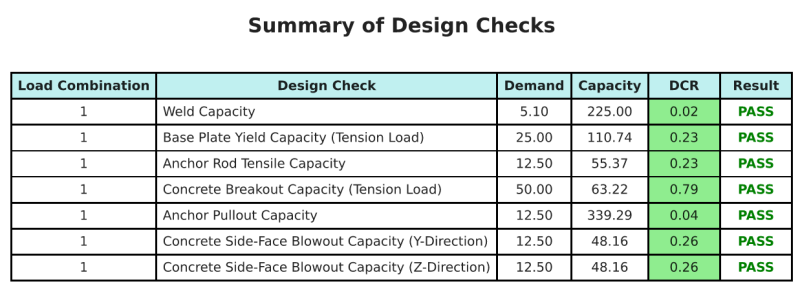
Relatório de amostra de Skyciv
Veja o nível de detalhe e clareza que você pode esperar de um relatório de design de placa base SkyCiv. O relatório inclui todas as principais verificações de projeto, equações, e resultados apresentados em um formato claro e fácil de ler. É totalmente compatível com os padrões de design. Clique abaixo para ver um exemplo de relatório gerado usando a calculadora de placa base SkyCiv.
Compre software de placa de base
Compre a versão completa do módulo de design da placa de base por conta própria, sem outros módulos Skyciv. Isso oferece um conjunto completo de resultados para o design da placa de base, incluindo relatórios detalhados e mais funcionalidade.