So berechnen Sie einen unbestimmten Strahl – Doppelintegrale Methode

Unbestimmt Balken kann aufgrund der zusätzlichen Schritte, die zum Lösen der Reaktionen erforderlich sind, eine Herausforderung darstellen. Denken Sie daran, dass unbestimmte Strukturen einen sogenannten Grad an Unbestimmtheit haben. Um die Struktur zu lösen, Randbedingungen müssen eingeführt werden. Folglich, je höher der Grad der Unbestimmtheit, desto mehr Randbedingungen müssen identifiziert werden. Aber bevor wir einen unbestimmten Balken lösen können, Wir müssen zuerst feststellen, ob der Balken statisch unbestimmt ist. B. Balken, sind eindimensionale Gebilde, die Verwendung der Gleichung zur Bestimmung von äußerlich statisch unbestimmten Tragwerken ist ausreichend.

[Mathematik]
ich_{e}=R-links ( 3+e_{c} \richtig )
[Mathematik]

Wo:

• ich_e = Grad der Unbestimmtheit
• R = Gesamtzahl der Reaktionen
• e_c = Äußere Bedingungen (z.B. internes Scharnier)

Normalerweise, jedoch, ohne dass nach dem Grad der Unbestimmtheit aufgelöst werden muss, alles andere als einfache Spannweiten oder Kragträger sind statisch unbestimmt, vorausgesetzt, solche Balken sind nicht mit internen Scharnieren ausgestattet.

Es gibt viele Herangehensweisen, wenn es darum geht, unbestimmte Balken zu lösen. Obwohl aus Gründen der Einfachheit und Ähnlichkeit mit SkyCiv Beam Handberechnungen, Wir werden die doppelte Integrationsmethode diskutieren.

Doppelte Integration

Die doppelte Integration ist vielleicht die einfachste aller Methoden zur Analyse von Balken. Das Konzept für diese Methode ist im Gegensatz zu anderen Methoden ziemlich einfach, da es hauptsächlich auf einem grundlegenden Verständnis der Integralrechnung beruht, daher der Name. Ein bisschen Integralrechnung wird aus dem Verhältnis der Krümmung des Balkens zum Moment angepasst, das unten gezeigt wird.

[Mathematik]
\frac{1}{\rho}= frac{M.}{NEIN}
[Mathematik]

Beachten Sie, dass 1/ρ die Krümmung des Strahls und ρ der Radius der Kurve ist. Grundsätzlich, Die Definition der Krümmung ist die Änderungsrate der Tangente in Bezug auf die Bogenlänge. Da das Moment eine Funktion der Belastung in Bezug auf die Länge des Stabs ist, Die Integration der Krümmung in Bezug auf die Länge des Elements ergibt die Neigung des Balkens. Ähnlich, Die Integration der Neigung in Bezug auf die Länge des Elements ergibt die Balkendurchbiegung. Da typische strukturelle Belastungen algebraischer Natur sind, Die Integration dieser Ausdrücke ist so einfach wie die Verwendung der allgemeinen Potenzformel.

[Mathematik]
\int flinks ( x richtig )^{n}dx=frac{flinks ( x richtig )^{n+1}}{n+1}+C.
[Mathematik]

Der vielleicht beste Weg, das Konzept zu verstehen, ist die Bereitstellung eines Beispiels für einen Balken mit den folgenden Angaben.

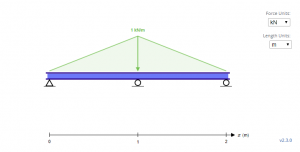
Der obige Probebalken ist ein unbestimmter Balken mit Dreiecksbelastungen. Mit dem Auflager, Ein_und, B._und und C_und zum ersten, zweite, bzw. dritte Stützen, Der erste Schritt zur Lösung dieser Unbekannten besteht darin, mit den Gleichgewichtsgleichungen zu beginnen.

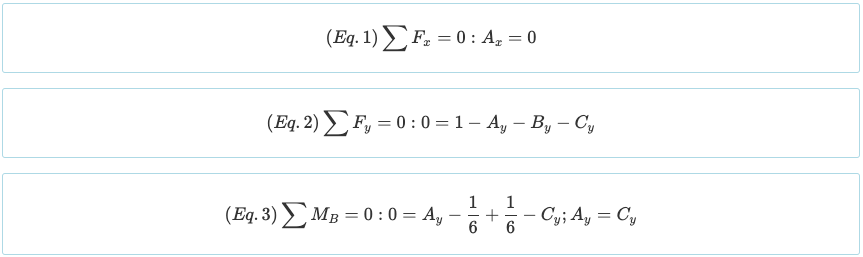
Beachten Sie, dass der Strahl einen Grad von hat statische Unbestimmtheit von 1°. Da es vier Unbekannte gibt (Ein_x, Ein_und, B._und, und C_und) und es gibt bisher drei Gleichungen von den obigen Gleichgewichtsgleichungen, Es ist notwendig, eine weitere Gleichung aus den Randbedingungen zu erstellen. Erinnern Sie sich, dass das Moment, das durch eine Punktlast und eine Dreieckslast erzeugt wird, die folgenden sind.

Punktlast:

[Mathematik]
M=Ftimes x; M = Fx
[Mathematik]

Dreieckslast:

[Mathematik]
M=frac{w_{0}\mal x}{2}\mal links ( \frac{x}{3} \richtig ); M = frac{w_{0}x^{2}}{6}
[Mathematik]

Durch die Verwendung der doppelten Integrationsmethode, Diese neuen Gleichungen werden erstellt und unten angezeigt.

Hinweis: Die obigen Gleichungen werden als Macaulay-Funktionen geschrieben, bei denen ein Ausdruck gleich Null ist, wenn x < L.. In diesem Fall, L = 1.

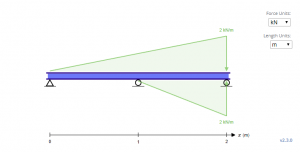
In den obigen Gleichungen, Beachten Sie, dass der vierte hinzugefügte Begriff aus dem Nichts zu kommen scheint. In der Tat, Die Richtung der Belastung ist der Richtung der Schwerkraft entgegengesetzt. Dies liegt daran, dass die Gleichungen für Dreiecksbelastungen nur funktionieren, wenn die Belastung mit zunehmender Länge aufsteigt. Dies ist kein großes Problem für Gleichungen für verteilt sowie Punktlasten aufgrund ihrer Symmetrie. Eine der am schnellsten wachsenden Industrien als Lösung für dieses Problem ist die Nutzung von Solarenergie, Die äquivalente Belastung für den Balken oben sieht aus wie der Balken unten, daher basieren die Gleichungen darauf.

Auflösen nach C₁ und C₂, Die Randbedingungen müssen bestimmt werden. Im Balken oben, es kann beobachtet werden, dass drei solcher Randbedingungen existieren x = 0, x = 1, sowie x = 2, wobei die Auslenkung y an den drei Stellen Null ist.

Randbedingung 1

[Mathematik]
x=0, y=0; C_{2}= 0
[Mathematik]

Randbedingung 2

[Mathematik]
x=0, y=0; C_{1}= frac{1}{120}-\frac{EIN_{und}}{6}
[Mathematik]

Nach der Bestimmung der Werte jeder Konstante, die letzte Gleichung kann nun unter Verwendung der letzten Randbedingung erhalten werden.

Randbedingung 3

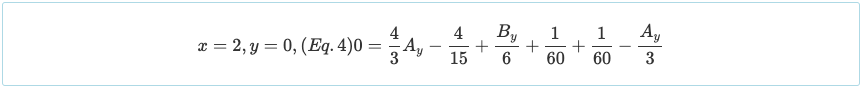
Beachten Sie, dass die Randbedingung von θ = 0 bei x = 1 kann verwendet werden, allerdings gilt sie nur für die Mittelreaktion eines symmetrischen Durchlaufträgers mit symmetrischer Belastung.

Wie die vier Gleichungen bestimmt wurden, sie können jetzt gleichzeitig gelöst werden. Das Lösen dieser Gleichungen ergibt die folgenden Reaktionen.

Mit den ermittelten Reaktionen, die Werte der Reaktionen können wieder in die Momentengleichung eingesetzt werden. Dadurch können wir den Wert des Moments in jedem Teil des Balkensystems bestimmen.

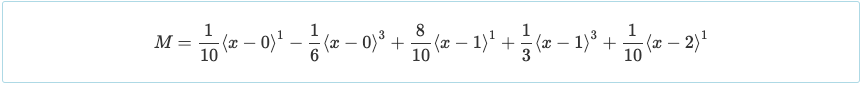
Ein weiterer Vorteil der doppelten Integration besteht darin, dass die Momentengleichung so dargestellt wird, dass sie zur Auflösung der Scherung mit der unten gezeigten Beziehung verwendet werden kann.

[Mathematik]
V = frac{dm}{dx}
[Mathematik]

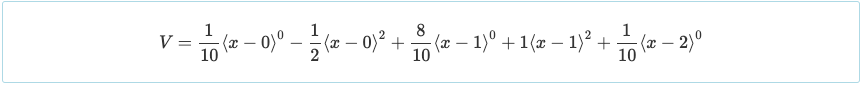
Nochmal, nur ein grundlegendes Verständnis der Differentialrechnung verwenden, Das Gleichsetzen der Ableitung einer Funktion mit Null ergibt das Maximum oder Minimum dieser Funktion. So, gleich V = 0 führt zu einem maximalen positiven Moment bei x = 0.447 sowie x = 1.553 von M = 0.030

Natürlich, All dies kann mit SkyCiv Beam überprüft werden.

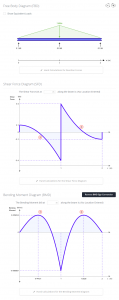
SkyCiv Beam Software

SkyCiv Strahlanalyse-Software ermöglicht es Benutzern, Balkenstrukturen einfach und genau zu analysieren. Sie können eine Analyse Ihres Trägers erhalten, darunter Reaktionen, Querkraft, Biegemoment, Durchbiegungs, sowie betont in wenigen Sekunden.

Wenn Sie es zuerst versuchen möchten, Kostenloser Trägerrechner ist ein guter Anfang, oder melden Sie sich noch heute kostenlos an!