Die Grundlagen des Schwerpunkts
Es ist wichtig zu beachten, dass auf einem Querschnitt, deren Fläche ist durchweg einheitlich, Der Schwerpunkt kann ermittelt werden, indem die Summe der Momente in Bezug auf eine beliebig festgelegte Achse ermittelt wird, wird aber normalerweise an der oberen oder unteren Faser eingestellt. Sehen Sie sich unseren vorherigen Artikel an wie man den Schwerpunkt findet eines Strahlabschnitts und SkyCiv Free Centroid Calculator.
Grundsätzlich, Der Schwerpunkt kann erhalten werden, indem die Summe der Momente über die Summe der Fläche genommen wird. Welches auf diese Weise ausgedrückt wird.
[Mathematik]
\Bar{x}= frac{1}{Ein}\int xf left ( x richtig )dx
[Mathematik]
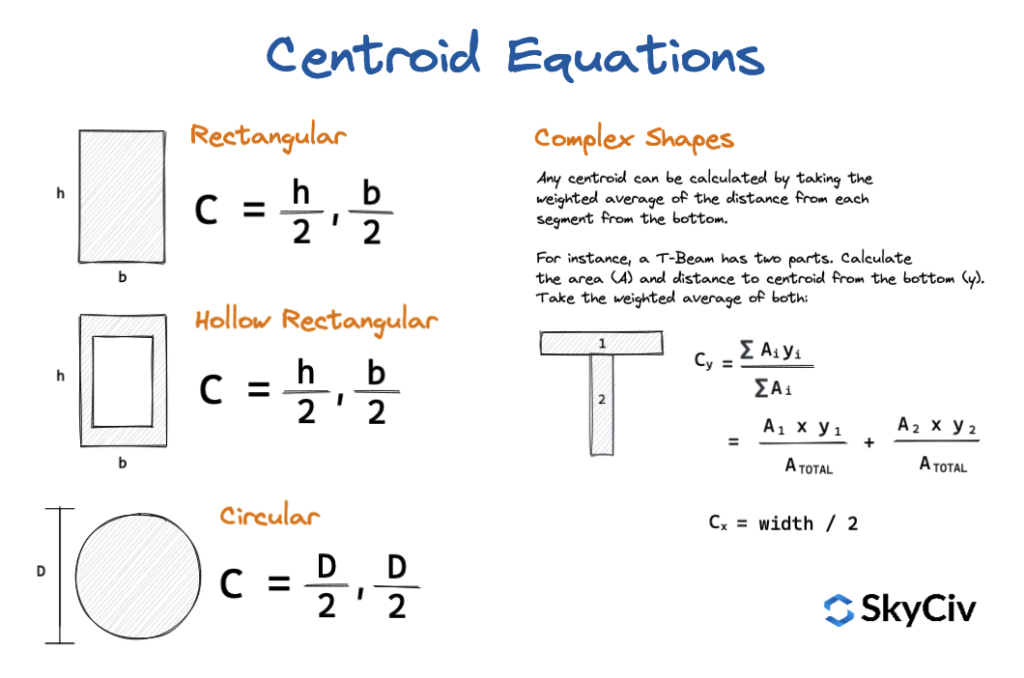
Zusammenfassung der Schwerpunktgleichungen
In der obigen Gleichung, f(x) ist die Funktion und x ist der Momentarm. Um dies besser zu veranschaulichen, Wir werden den y-Schwerpunkt eines beliebigen Dreiecks ableiten, dessen Basis mit der x-Achse zusammenfällt. In dieser Situation, die Form des Dreiecks, ob es gleichseitig ist, gleichschenklig oder skalen ist irrelevant, da sich alles nur auf die x-Achse bezieht. Beachten Sie, dass die Form irrelevant ist, wenn die Basis des Dreiecks in Bezug auf die Achse zusammenfällt oder parallel ist. Dies ist bei der Lösung des x-Schwerpunkts nicht der Fall. Stattdessen, Sie können sich vorstellen, den Schwerpunkt zweier rechtwinkliger Dreiecke in Bezug auf die y-Achse zu erhalten. Einfachheitshalber, Stellen wir uns ein gleichschenkliges Dreieck vor, das der folgenden Referenztabelle ähnelt. Das Finden der Beziehung zwischen b und h ergibt die folgende Beziehung.
[Mathematik]
\frac{-j}{x}= frac{-h}{b}
[Mathematik]
Beachten Sie, dass die Steigung negativ ist, da wir uns das Dreieck als aufrecht vorstellen. Wenn wir uns vorstellen, dass das Dreieck invertiert ist, Die Steigung wäre positiv. Ungeachtet, Die Beziehung bleibt dieselbe. Als x = f(j), Die obige Beziehung kann wie folgt umgeschrieben werden.
[Mathematik]
x = f left ( y richtig )= frac{b}{h}j
[Mathematik]
Wir können jetzt nach Schwerpunkt lösen. Anpassen der ersten Gleichung oben, wir bekommen folgendes.
[Mathematik]
\Bar{j}= frac{1}{Ein}\int yf left ( y richtig )zwei
[Mathematik]
Das Einstecken zusätzlicher Werte und das Ersetzen der obigen Beziehung ergibt die folgende Gleichung.
[Mathematik]
\Bar{j}= frac{2}{bh}\int_{0}^{h} \frac{b}{h}und ^{2}zwei
[Mathematik]
Vereinfachen,
[Mathematik]
\Bar{j}= frac{2}{h ^{2}}\links [ \frac{und ^{3}}{3} \richtig ]_{0}^{h}
[Mathematik]
[Mathematik]
\Bar{j}= frac{2}{h ^{2}}\links [ \frac{h ^{3}}{3}-0 \richtig ]
[Mathematik]
[Mathematik]
\Bar{j}= frac{2}{3}h
[Mathematik]
Beachten Sie, dass diese Lösung von oben übernommen wird. Der von unten genommene Schwerpunkt muss dann gleich sein 1/3 von h.
Formel für Schwerpunkte gängiger Formen und Balkenabschnitte
Unten ist eine Liste von a Vielzahl von Balkenquerschnittsformen und der Abstand zu den Schwerpunkten des Abschnitts. Die Gleichungen zeigen, wie der Schwerpunkt eines bestimmten Abschnitts von der Basis oder dem am weitesten links liegenden Punkt des Abschnitts ermittelt wird. Für SkyCiv Student- und Strukturabonnements, Diese Referenz kann auch als PDF-Referenz heruntergeladen werden, um sie überall hin mitzunehmen. Zentroide eines Strahlabschnitts sind äußerst wichtig, da sie die neutrale Achse lokalisieren und einer der frühesten Schritte sind, die bei der Analyse eines Strahlabschnitts erforderlich sind.
SkyCiv bietet auch eine umfassende Zusammenfassung der Abschnittstabelle, die alle Gleichungen und Formeln in Bezug auf Balkenabschnitte enthält (Trägheitsmoment, Bereich etc.…).
Die Gleichung für verschiedene Schwerpunkte ist unten aufgeführt:
| REFERENZ | C.j (Abstand vom Boden) |
C.x (Entfernung vom äußersten linken Punkt) |
Schwerpunkt der rechteckigen oder rechteckigen Abschnitte |
||
|---|---|---|
 |
[Mathematik] \dfrac{h}{2} [Mathematik] |
[Mathematik] \dfrac{b}{2} [Mathematik] |
Schwerpunkt eines hohlen rechteckigen Abschnitts |
||
 |
[Mathematik] \dfrac{b}{2} [Mathematik] |
[Mathematik] \dfrac{h}{2} [Mathematik] |
Schwerpunkt eines Kreises oder Kreisabschnitts |
||
 |
[Mathematik] \dfrac{D.}{2} [Mathematik] |
[Mathematik] \dfrac{D.}{2} [Mathematik] |
Schwerpunktgleichung eines hohlen Kreisabschnitts |
||
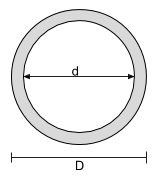 |
[Mathematik] \dfrac{D.}{2} [Mathematik] |
[Mathematik] \dfrac{D.}{2} [Mathematik] |
Schwerpunkt eines gleichschenkligen Dreiecks |
||
 |
[Mathematik] \dfrac{h}{3} [Mathematik] |
[Mathematik] \dfrac{b}{2} [Mathematik] |
Schwerpunkt eines I-Trägers |
||
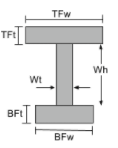 |
[Mathematik] \frac{TFw times TFt times left ( BFt + Wh + \frac{TFt}{2} \richtig )}{TFw times TFt + Wt times Wh + BFw times BFt} + [Mathematik] [Mathematik] \frac{Wt times Wh times left ( BFt + \frac{Wh}{2} \richtig )}{TFw times TFt + Wt times Wh + BFw times BFt} + [Mathematik] [Mathematik] \frac{BFw times BFt times left ( \frac{BFt}{2} \richtig )}{TFw times TFt + Wt times Wh + BFw times BFt} [Mathematik] |
[Mathematik] TFw > BFw, \frac{TFw}{2}[Mathematik] [Mathematik] BFw > TFw, \frac{BFw}{2} [Mathematik] |
Schwerpunkt eines T-Abschnitts |
||
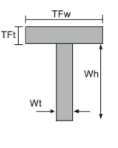 |
[Mathematik] \frac{Wt times Wh times left ( \frac{Wh}{2} \richtig )}{TFw times TFt + Wt times Wh } + [Mathematik] [Mathematik] \frac{TFw times TFt times left ( Wh + \frac{TFt}{2} \richtig ) }{TFw times TFt + Wt times Wh } [Mathematik] |
[Mathematik] \frac{TFw}{2} [Mathematik] |
Schwerpunkt eines Kaiserschnitts |
||
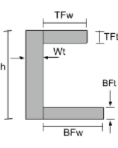 |
[Mathematik] \frac{TFw times TFt times left ( h – \frac{TFt}{2} \richtig )}{TFw times TFt + Wt times Wh + BFw times BFt} + [Mathematik] [Mathematik] \frac{Wt times h times left ( \frac{h}{2} \richtig )}{TFw times TFt + Wt times Wh + BFw times BFt} + [Mathematik] [Mathematik] \frac{BFw times BFt times left ( \frac{BFt}{2} \richtig )}{TFw times TFt + Wt times Wh + BFw times BFt} [Mathematik] |
[Mathematik] \frac{TFt times TFw times left ( Wt + \frac{TFw}{2} \richtig )}{TFt times TFw + h mal Wt + BFt times BFw} + [Mathematik] [Mathematik] \frac{h times Wt times left ( \frac{Wt}{2} \richtig )}{TFt times TFw + h mal Wt + BFt times BFw} + [Mathematik] [Mathematik] \frac{BFt times BFw times left ( Wt + \frac{BFw}{2} \richtig )}{TFt times TFw + h mal Wt + BFt times BFw} [Mathematik] |
Schwerpunkt eines Winkels |
||
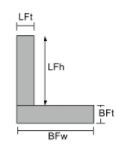 |
[Mathematik] \frac{LFt times LFh times left ( BFt + \frac{LFh}{2} \richtig ) }{LFt times LFh + BFw times BFt} + [Mathematik] [Mathematik] \frac{BFw times BFt times left ( \frac{BFt}{2} \richtig )}{LFt times LFh + BFw times BFt} [Mathematik] |
[Mathematik] \frac{LFh times LFt times left ( \frac{LFt}{2} \richtig )}{LFh times LFt + BFt times BFw} + [Mathematik] [Mathematik] \frac{BFt times BFw times left ( \frac{BFw}{2} \richtig )}{LFh times LFt + BFt times BFw} [Mathematik] |
Automatische Gleichungen für den Strahlschwerpunkt
Schauen Sie sich unsere an Kostenloser Schwerpunktrechner, eine vereinfachte Version von SkyCiv Section Builder, zur automatischen Berechnung des Strahlschwerpunkts, ohne dass manuelle Berechnungen erforderlich sind. Oder melden Sie sich noch heute an, um loszulegen!


