Nachfolgend finden Sie ein Beispiel für einige Grundplattenberechnungen nach philippinischem Code, die häufig bei der Konstruktion von Grundplatten verwendet werden. Oft beim Entwerfen von Grundplatten, Betrachten wir einige unterschiedliche Prüfungen in Bezug auf die verschiedenen Komponenten einer Grundplatte, nämlich:
- Die Betonbasis – generell gegen Lager- und Druckkräfte in Anlehnung an NSCP geprüft 2015
- Die Schweißnähte – Schweißnähte müssen überprüft werden, um sicherzustellen, dass sie eine angemessene Zurückhaltung bieten und nicht unter Stress für NSCP versagen 2015
- Ankerschrauben – kann aus verschiedenen Gründen fehlschlagen, wie unten in den Berechnungsbeispielen für Ankerschrauben gemäß NSCP gezeigt 2015
- Mitglied aus Stahl (Spalte) prüft – normalerweise basierend auf lokalen Stahlkonstruktionsstandards
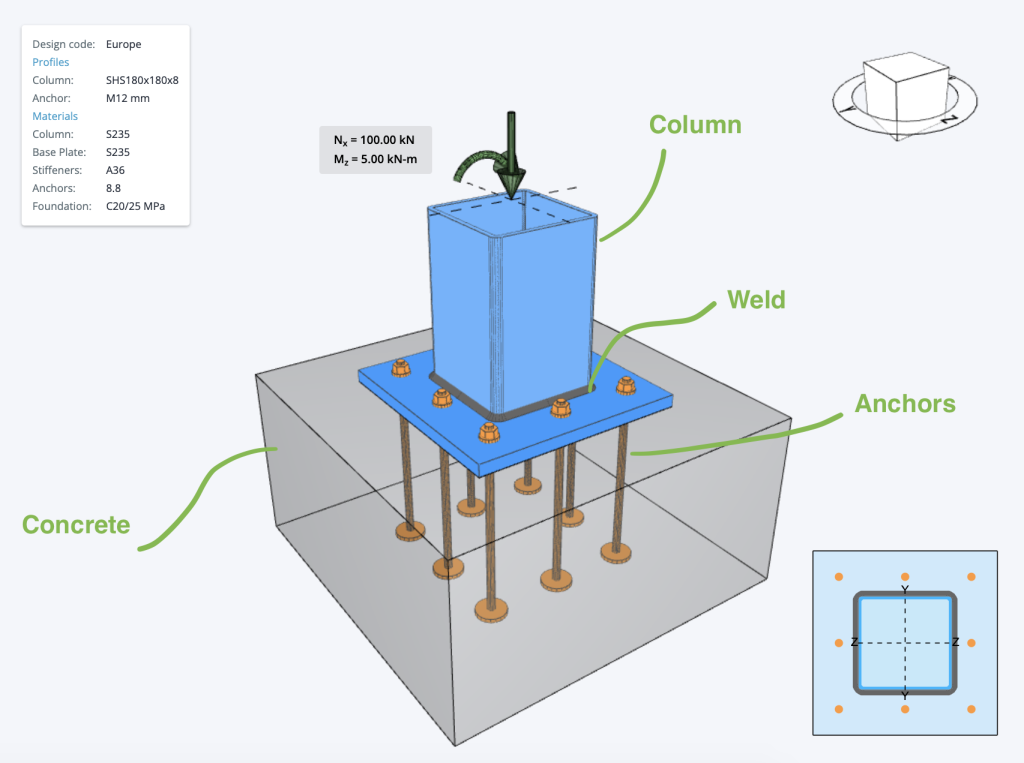
Zur Zeit, bleibt die Design der Grundplatte aus Stahl -Modul implementiert die folgenden Prüfungen unten. Die kostenpflichtige Version dieser Software, enthält detaillierte Schritt-für-Schritt-Berechnungen, damit Ingenieure genau überprüfen können, wie diese Berechnungen durchgeführt werden!
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
Lastkombinationen:
Mit der Design der Grundplatte aus Stahl das verwendet faktorisierte Lastkombinationen unter NSCP 2015 gilt wie folgt:
- \(1.4D)
- \(1.2D. + 1.6L. + 0.5(L_{r} \Text{ oder } R.)\)
- \(1.2D. + 1.6(Lr text{ oder } R.) + (f1L text{ oder } 0.5W.)\)
- \(1.2D. + 1.0W. + f1L + 0.5(Lr \ \Text{ oder } R.)\)
- \(1.2D. + 1.0E. + f1L)
- \(0.9D. + 1.0W)
- \(0.9D. + 1.0E)
wo :
\(D) = Eigenlast
\(L) = Nutzlast
\(L_{r}\) = Dachnutzlast
\(R) = Regenlast
\(E) = Erdbeben
\(W) = Windlast
\(f_{1}\) = Nutzlastfaktor (Standardwert = 1, Siehe NSCP 2015 Sektion 203.3.1)
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
NSCP 2015 Betonlagerprüfung:
Mit der Design der Grundplatte aus Stahl prüft die Betontragfähigkeit (Druck-) Design in gemäß NSCP 2015 Gl. 510.8-2.
\( F_{b} = phi_{Lager} \mal 0.85 \mal f’_{c} \mal sqrt{ \frac{ EIN_{2} }{ EIN_{1} } } \leq F_{b, Grenze} = 1.70 \mal f_{c} \mal A_{1} \)
wo:
\( f’_{c} \) – Betondruckfestigkeit
\( EIN_{1} \) – Bodenplattenbereich in Kontakt mit der Betonoberfläche
\( EIN_{2} \) – Betonauflagefläche
\( \phi_{Lager} \) – Widerstandsfaktor für Beton ( Standardwert= 0.65 )
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
NSCP 2015 Prüfung der Schweißnahtkonstruktion:
Mit der Design der Grundplatte aus Stahl prüft das Schweißdesign gemäß NSCP 2015 Gleichung 510.2-3
\( (ich) R_{n} = R_{Null} + R_{nwt} \)
oder
\( (ii) R_{n} = 0,85R_{Null} + 1.5R_{nwt} \)
wo:
\(R_{Null} \) = Gesamtnennfestigkeit längsbelasteter Kehlnähte.
\(R_{nwt} \) = Gesamtnennfestigkeit querbelasteter Kehlnähte.
Wir dachten, es wäre eine gute Idee, ein Beispiel für das Modellieren von Anfang bis Ende durchzugehen:
NSCP 2015 Anker-Design-Check:
Mit der Design der Grundplatte aus Stahl prüft Ankerparameter gilt unter Verwendung von Code-Bestimmungen von NSCP 2015 Sektion 417 | Verankerung an Beton.
Die folgenden Widerstände von Ankerschrauben werden bewertet:
- Stahlfestigkeit des Ankers bei Zug und Schub, \( \phi N_{zu} \) und \( \phi V_{zu} \).
- Betonbruchfestigkeit bei Zug und Schub, \( \phi N_{cbg} \) und \( \phi V_{cbg} \).
- Betonauszugsfestigkeit, \( \phi N_{p} \).
- Betonausbruchfestigkeit des Ankers bei Schub, \( \phi V_{cp} \).
Stahlfestigkeit des Ankers bei Zug und Schub
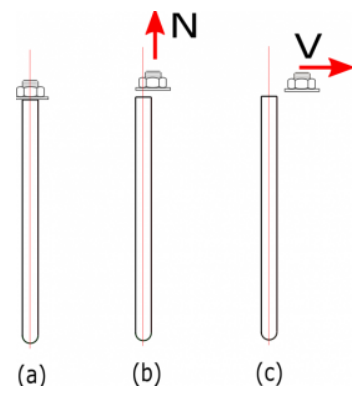
Die gewichtete Stahlfestigkeit des Ankers bei Zug und Scherung wird gemäß NSCP bestimmt 2015 Sektion 417.4.1 wie
Für Spannung
\( \phi_{Spannung, anc} N_{zu} = phi_{Spannung, anc} EIN_{ich weiß,N.}f_{uta} \rechter Pfeil \) Gleichung 17.6.1.2
Für Schere
\( \phi_{Schub-, anc} V_{zu} = phi_{Schub-, anc} 0.6EIN_{ich weiß,V }f_{uta} \rechter Pfeil \) Gleichung 17.7.1.2b
wo:
- \( \phi_{Spannung, anc} \) – Festigkeitsminderungsfaktor für Anker unter Zug ( Standardwert = 0.75 )
- \( \phi_{Schub-, anc}\) – Festigkeitsminderungsfaktor für Dübel unter Schub ( Standardwert = 0.65 )
- \( EIN_{ich weiß,N.}\) – ist die wirksame Querschnittsfläche eines Dübels unter Zug.
- \( EIN_{ich weiß,V }\) – ist die wirksame Querschnittsfläche eines Dübels unter Schub.
- \( f_{uta}\) – angegebene Zugfestigkeit des Ankerstahls und darf nicht größer sein als \(1.9f_{Ja}\) und 125 KSI (861.845 Mpa)
Betonbruchfestigkeit
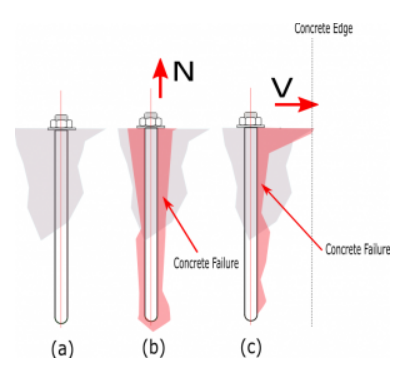
Die faktorisierte Betonausbruchfestigkeit des Ankers bei Zug und Scherung wird gemäß NSCP bestimmt 2015 Gleichung 417.4.2.1b und NSCP 2015 Gleichung 417.5.2.1b wie
\( \phi N_{cbg} = phifrac{ EIN_{Nc} }{ EIN_{Merken} } \psi_{ec,N.} \psi_{ed,N.} \psi_{c,N.} \psi_{cp,N.} N_{b} \rechter Pfeil \) 417.4.2.1b
wo:
\( \phi \) – Festigkeitsminderungsfaktor für Dübel unter Zug ( Standardwert = 0.75 ).
\( EIN_{Nc} \) – projektierter Betonversagen eines Einzel- oder Gruppenankers.
\( EIN_{Merken} \)- Projektbetonbruchbereich eines einzelnen Dübels, zur Berechnung der Zugfestigkeit, wenn nicht durch Randabstand oder -abstand begrenzt.
\( \psi_{ec,N.} \) – Faktor, der verwendet wird, um die Zugfestigkeit von Ankern basierend auf der Exzentrizität der aufgebrachten Lasten zu modifizieren.
\( \psi _{ec,N.} = frac{1.00}{ 1 + \frac{2 \mal e^{„}_{N.}}{3 \mal h_{ef}} } \leq 1.00 \rechter Pfeil \) Gleichung 417.4.5.3
\( \psi_{ed,N.} \) – Faktor zur Änderung der Zugfestigkeit des Ankers.
(ein) \( \Text{wenn } C_{ein,Min.} \geq 1,5h_{ef} \Text{ dann } \psi _{ed,N.} = 1.00 \)
und
(b) \( \Text{wenn } C_{ein,Min.} < 1.5h_{ef} \Text{ dann } \psi _{ed,N.} = 0.70 + 0.3\frac{C_{ein,Min.}}{1.5h_{ef}} \) Gleichung 417.4.2.5b
\( \psi_{c,N.} \) – Breakout-Cracking-Faktor bei Spannung.
\( \psi _{c,N.} = 1.25 \) für einbetonierte Anker
\( \psi_{cp,N.} \) – Bruchspaltfaktor bei Spannung.
(ein) \( \Text{wenn } C_{ein,Min.} \geq C_{ac} \Text{ dann } \psi _{cp,N.} = 1.00 \) Gleichung 17.6.2.4.1a
und
(b) \( \Text{wenn } C_{ein,Min.} < C_{ac} \Text{ dann } \psi _{cp,N.} = frac{ C_{ein,Min.} }{ C_{ac}} \geq frac{ 1.5h_{ef} }{ C_{ac} } \) Gleichung 17.6.2.4.1b
\( N_{b} \) – Grundbetonausbruchfestigkeit im Zug eines Einzeldübels in gerissenem Beton.
Betonauszugsfestigkeit
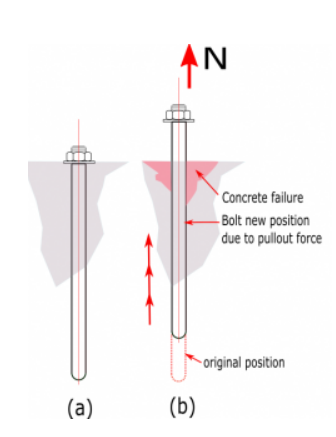
Die faktorisierte Betonauszugsfestigkeit eines Dübels ist in NSCP definiert 2015 Gleichung 417.4.3.4 wie
Npn = φΨc,P. N.p
wo:
\( \phi \) – Festigkeitsminderungsfaktor für Dübel unter Zug ( Standardwert = 0.70 ).
\( \psi _{c, P.} \) – Modifikationsfaktor für Betonzustand
Für gerissenen Beton:
\( \psi _{c, P.} \) = 1.0
Für ungerissenen Beton:
\( \psi _{c, P.} \) = 1.4
\( N_{p} \) – Ankerauszugsstärke
Für gerissenen Beton:
\( N_{p} = 8A_{brg}f^{„}_{c}\rechter Pfeil \) Gleichung 417.4.3.4
Für ungerissenen Beton:
\( N_{p} = 0,9f^{„}_{c}e_{h}d_{ein} \rechter Pfeil \) Gleichung 417.4.3.5
wo \( 3d_{ein} \leq e_{h} \leq 4.5d_{ein} \)
\( f^{„}_{c} \) – spezifizierte Druckfestigkeit von Beton.
\( EIN_{brg} \) – Nettoauflagefläche des Bolzenkopfes, Ankerschraube oder verformter Stab mit Kopf.
\( e_{h} \) – Abstand von der Innenfläche des Schafts eines J-Bolzens oder L-Bolzens bis zur Außenspitze des J- oder L-Bolzen.
\( d_{ein} \) – Außendurchmesser Dübel bzw. Schaftdurchmesser Kopfbolzen head, Kopfschraube, oder Hakenschraube.


