Inhoudsopgave
- Overzicht – Wat is het traagheidsmoment
- Voorbeeld – Hoe het traagheidsmoment te berekenen
- Formule en vergelijkingen
- Rekenmachines
- Oefen vragen
Overzicht – Wat is het traagheidsmoment?
In het kader van de bouwkunde, het traagheidsmoment is een doorsnede-eigenschap die wordt gebruikt om het vermogen van een constructie-element om weerstand te bieden aan buig- en torsiekrachten te bepalen. Het is meestal een redelijk goede indicator voor de stijfheid en sterkte van de secties onder belasting. Een hoger traagheidsmoment betekent dat de constructie beter bestand is tegen buigen en doorbuigen, waardoor het een essentiële factor is bij het ontwerpen van balken, kolommen, en andere dragende onderdelen. Als kanttekening: Soms wordt dit ten onrechte gedefinieerd als het tweede moment van luiheid, maar dit is onjuist. De andere namen voor traagheidsmoment zijn: traagheidsmoment van het gebied, of tweede moment van Oppervlakte.
Voorbeeld – Hoe Bereken je het Traagheidsmoment van een Balkdoorsnede
Voordat we het traagheidsmoment van een balkdoorsnede kunnen bepalen (ook wel het tweede oppervlaktemoment van een balkdoorsnede genoemd), moet het zwaartepunt (of massamiddelpunt) bekend zijn. Bijvoorbeeld, als het traagheidsmoment van de sectie ten opzichte van de horizontale (XX) as vereist was, dan zou eerst het verticale (j) zwaartepunt nodig zijn (bekijk onze tutorials over het berekenen van het zwaartepunt van een balkdoorsnede en het berekenen van het statische/eerste oppervlaktemoment).
Voordat we beginnen, als je op zoek was naar onze Gratis Traagheidsmoment Calculator klik dan op de link om meer te leren. Deze zal het zwaartepunt, traagheidsmoment, en andere resultaten berekenen en zelfs de stap-voor-stap berekeningen laten zien! Maar voor nu, laten we kijken naar een stap-voor-stap handleiding en voorbeeld van hoe je het traagheidsmoment berekent:
Stap 1: Segmenteer de Balkdoorsnede in Delen
Bij het berekenen van het oppervlaktemoment van traagheid, moeten we het traagheidsmoment van kleinere segmenten berekenen. Probeer ze op te splitsen in eenvoudige rechthoekige secties. Bijvoorbeeld, de I-balk sectie hieronder, die ook in onze zwaartepunt tutorial te zien was. We hebben ervoor gekozen om deze sectie op te splitsen in 3 rechthoekige segmenten:
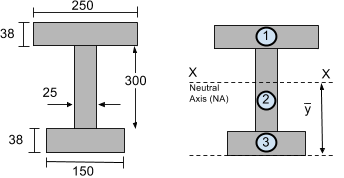
Stap 2: Bereken de neutrale as (NA)
De Neutrale As (NA) of de horizontale XX-as bevindt zich op het zwaartepunt of massamiddelpunt. In onze tutorial over het zwaartepunt, werd het zwaartepunt van deze sectie eerder gevonden op 216.29 mm van de onderkant van de sectie – dit wordt behandeld in onze het vinden van het zwaartepunt van een vorm tutorial. Deze kunnen ook eenvoudig worden berekend met onze zwaartepunt calculator of uit gangbare zwaartepuntvergelijkingen.
Het berekenen van het zwaartepunt, of de Neutrale As, is essentieel bij hoe het traagheidsmoment van een balk te berekenen, omdat dit de as is waarop het traagheidsmoment werkt.
Stap 3: Bereken het traagheidsmoment
Om het totale traagheidsmoment van de sectie te berekenen, moeten we de “Parallelle As Stelling”:

Omdat we het in drie rechthoekige delen hebben gesplitst, moeten we het traagheidsmoment van elk van deze secties berekenen. Het is algemeen bekend dat de traagheidsmomentequatie van een rechthoek ten opzichte van zijn zwaartepuntsas eenvoudigweg is:
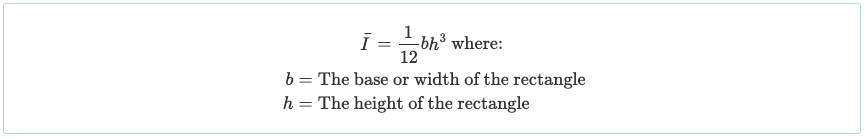
Het traagheidsmoment van andere vormen wordt vaak vermeld in de voor- of achterkant van leerboeken of in deze gids over traagheidsmoment vormen. de rechthoekige vorm is zeer gebruikelijk voor balksecties, dus het is waarschijnlijk de moeite waard om te onthouden.
Nu hebben we alle informatie die we nodig hebben om de “Parallelle As Stelling” te gebruiken en het totale traagheidsmoment van de I-balk sectie te vinden. In ons traagheidsmoment voorbeeld:

Dus daar heb je onze handleiding over het berekenen van het oppervlaktemoment voor balksecties. Dit resultaat is cruciaal in de constructieve engineering en is een belangrijke factor in de doorbuiging van een balk. We hopen dat je genoten hebt van de tutorial en kijken uit naar eventuele opmerkingen die je hebt. Voor meer informatie, bezoek onze tutorial op Traagheidsmoment Formule en vergelijkingen.
Formule en vergelijkingen
Elk sectietype (rechthoekig, I-balk, Circulaire) heeft zijn eigen formule voor snelle berekening. Dit zijn vereenvoudigde vergelijkingen waarmee ingenieurs deze belangrijke eigenschap snel en eenvoudig kunnen berekenen.
De vergelijkingen zijn een vereenvoudigde uitdrukking van de bovenstaande stappen. Bijvoorbeeld, de formule voor het traagheidsmoment van een holle rechthoek is in feite het traagheidsmoment van het grotere gedeelte – hoe kleiner (intern) sectie:

[wiskunde] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [wiskunde]
SkyCiv heeft een handige bron voor gemeenschappelijk gebruik samengesteld Formule van traagheidsmoment.
Rekenmachines
Er zijn veel manieren om het traagheidsmoment te berekenen, waarvan één is om software te gebruiken om het proces te vergemakkelijken.
SkyCiv Sectiebouwer is een volledig capabele sectieontwerptool die veel verder gaat dan de traagheidsmomentcalculator. Het laat u ook stapsgewijze berekeningen zien hoe u het traagheidsmoment kunt vinden:
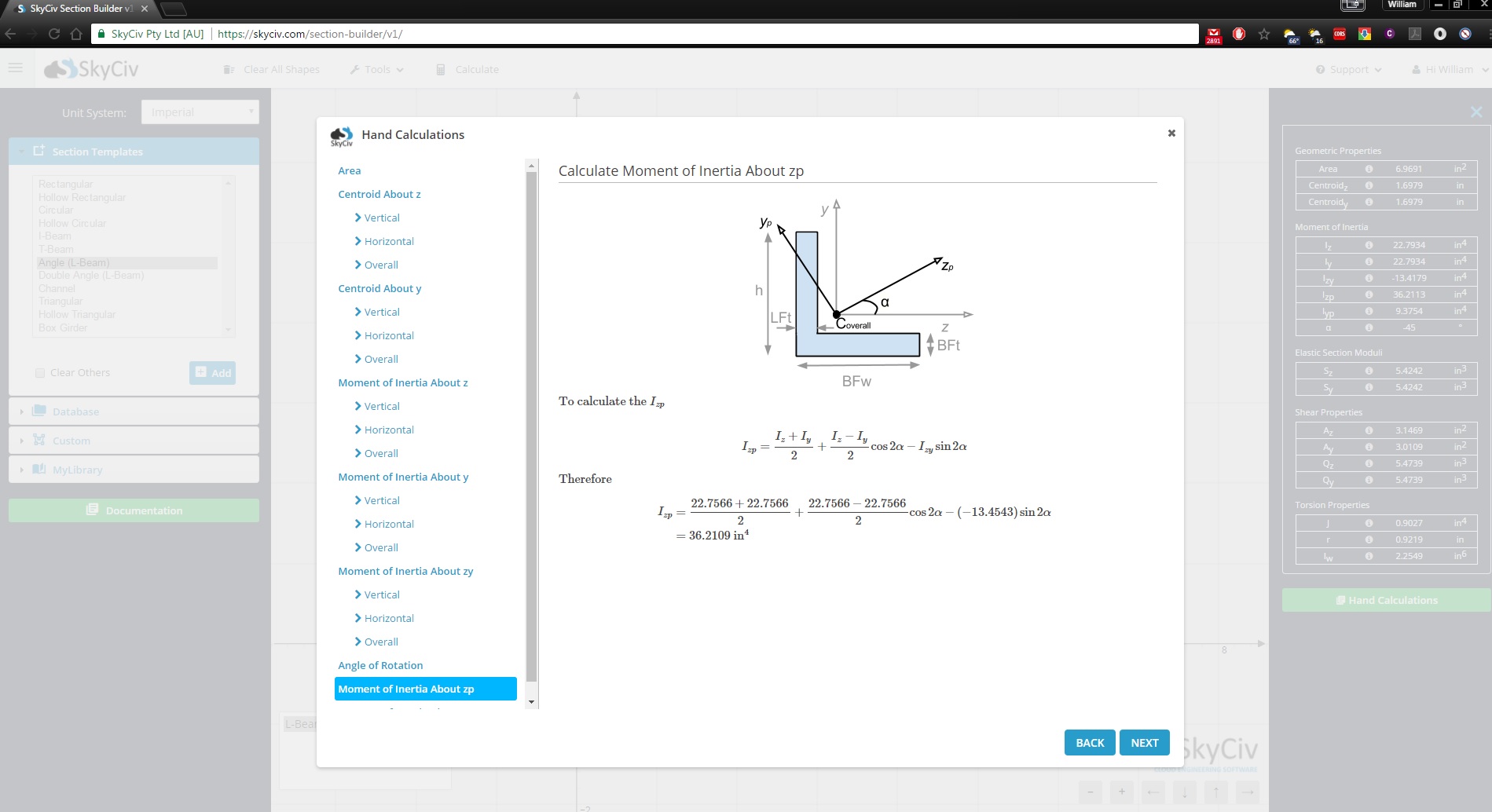
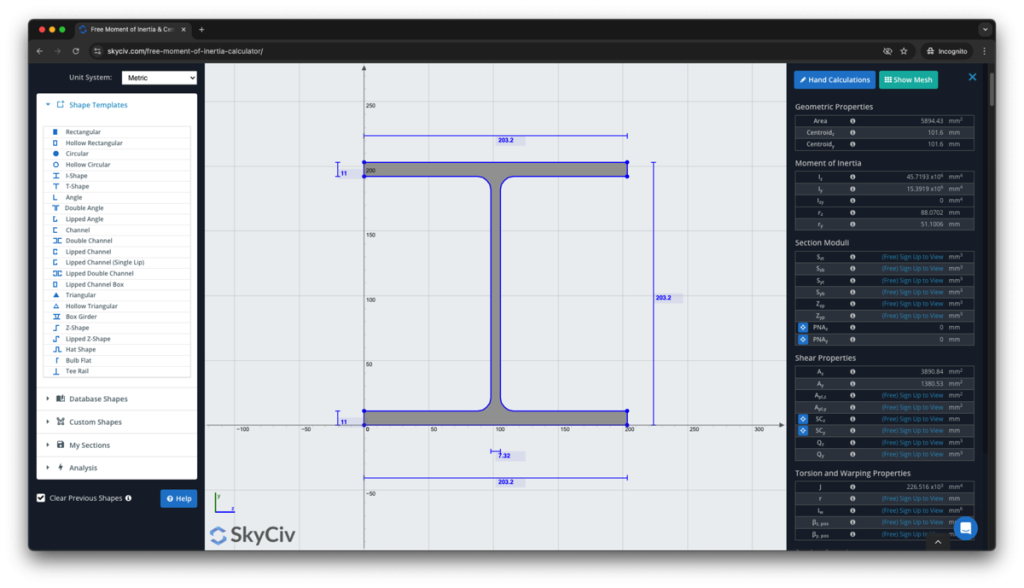
Meld je vandaag aan om meer te ontdekken over SkyCiv software, of boek een GRATIS DEMO om geholpen te worden met je engineering projecten voor bestaande gebruikers!
Bovendien, SkyCiv heeft een gratis Sectie-eigenschapscalculator als onderdeel van de Quick Design-bibliotheek. Het is een vereenvoudigd hulpmiddel, maar berekent ook het traagheidsmoment van gewone sectievormen.
Oefen vragen
Vraag 1: Rechthoekige sectie
Probleem: Bereken het traagheidsmoment (Ixx en Iyy) voor een rechthoekig gedeelte met een breedte (b) van 200 mm en een hoogte (h) van 300 mm.
Oplossing: De formules voor het traagheidsmoment voor een rechthoek zijn::
Vervanging van de gegeven waarden:
- b=200 mm
- h=300 mm
Voor Ixx:
Voor Iyy:
Vraag 2: I-Beam
Probleem: Bereken het traagheidsmoment van de hoofdas (Ixx) van een I-balkprofiel met de volgende afmetingen:
- Breedte bovenflens (TFw) = 6 in
- Dikte van de bovenste flens (TFt) = 0.43 in
- Sectiediepte = 6 in
- Webdikte (Wt) = 0.29 in
- Breedte onderste flens (BFw) = 6 in
- Dikte onderste flens (BFt) = 0.43 in
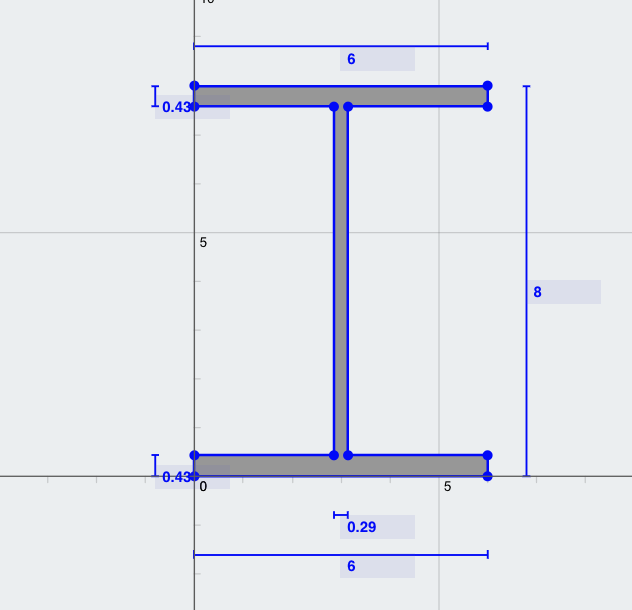
Oplossing:


