Inhoudsopgave

• Berekening van Buigmomentdiagram
• Buigmomentdiagram Berekenen met de Hand
• Tekenconventie voor Buigmomentdiagrammen
• Buiging Berekenen met SkyCiv Beamm

Berekening van Buigmomentdiagram

Hieronder volgen eenvoudige instructies voor het berekenen van het buigmomentdiagram van een eenvoudig ondersteunde balk. Bestudeer deze methode goed, want deze is zeer veelzijdig (en kan worden aangepast aan veel verschillende soorten problemen). Het vermogen om het moment van een balk te berekenen is een veelvoorkomende praktijk voor constructeurs en komt vaak voor in examens op hogescholen en middelbare scholen. Het is goed om te weten, dat de SkyCiv Beam-software deze handmatige berekeningen direct en automatisch kan weergeven! We volgen de tutorial van vandaag met een voorbeeld uit de Handberekeningsmodule van SkyCiv Beam.

Ten eerste, wat is een buigmomentt? en moment is een roterende kracht die optreedt wanneer een kracht loodrecht wordt uitgeoefend op een punt op een bepaalde afstand van dat punt. Het wordt berekend als de loodrechte kracht vermenigvuldigd met de afstand vanaf het punt. Een buigmoment is simpelweg de buiging die optreedt in een balk als gevolg van een moment.

Het is belangrijk om twee dingen te onthouden bij het berekenen van buigmomenten; (1) de standaard eenheden zijn Nm en (2) wanneer de bovenste vezel wordt samengedrukt, wordt de buiging als positief beschouwd. Met de definities uit de weg, laten we kijken naar de stappen om een buigmomentdiagram te berekenen:

Gratis Balk Calculator

Buigmomentdiagram Berekenen met de Hand

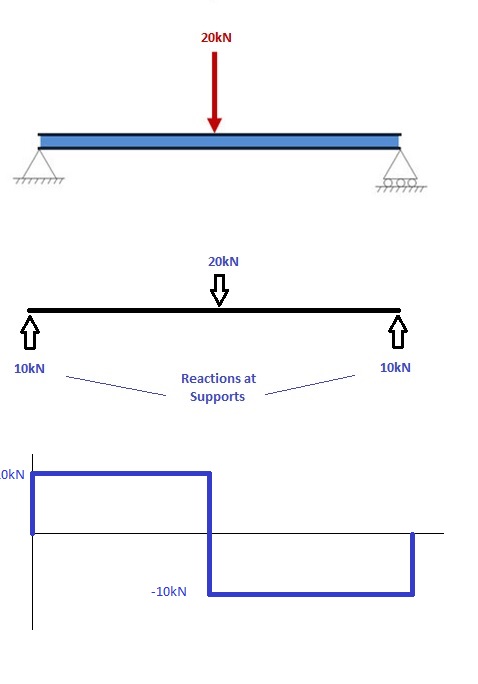
1. Bereken reacties bij de steunpunten en teken het Vrije Lichaam Diagram (FBD)

Als je niet zeker weet hoe je de reacties bij de steunpunten moet bepalen – bekijk dan eerst deze tutorial. Zodra je de reacties hebt, teken je je Vrije Lichaam Diagram en het Dwarskracht diagram onder de balk. Het berekenen van de momenten kan vervolgens in de volgende stappen worden gedaan:

2. Van links naar rechts, maak “snedes” voor en na elke reactie/belasting

Om het buigmoment van een balk te berekenen, moeten we werken zoals we deden voor het Schuifkracht Diagram. Beginnend bij x = 0 bewegen we langs de balk en berekenen we het buigmoment op elk punt.

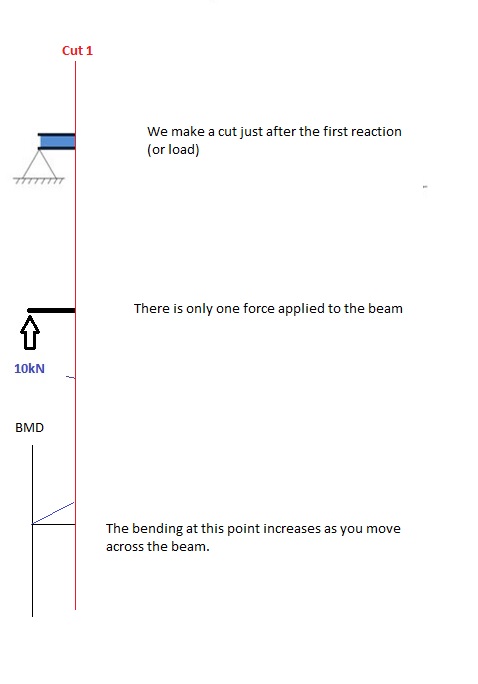
Snede 1

Maak een “snede” net na de eerste reactie van de balk. In ons eenvoudige voorbeeld:

Dus, wanneer we de balk doorsnijden, beschouwen we alleen de krachten die links van onze snede worden uitgeoefend. In dit geval, hebben we een kracht van 10 kN in de opwaartse richting. Zoals je je herinnert, is een buigmoment simpelweg de kracht x afstand. Dus naarmate we verder van de kracht af bewegen, zal de grootte van het buigmoment toenemen. We kunnen dit zien in ons buigmomentdiagram. De vergelijking voor dit deel van ons buigmomentdiagram is:

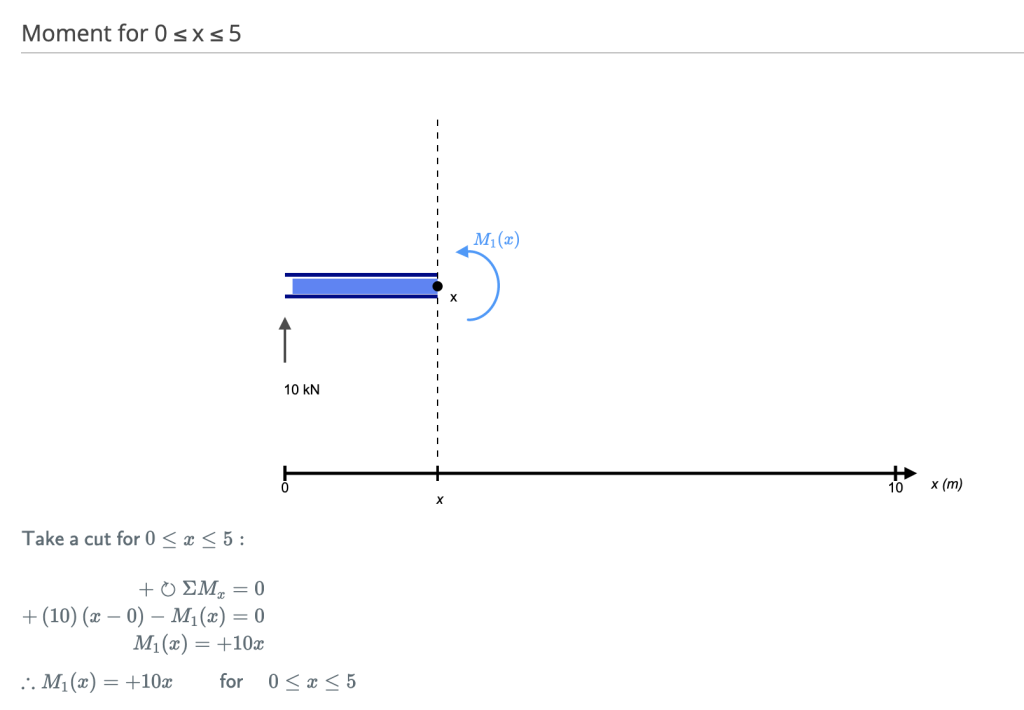
[Bron: SkyCiv Beam Handberekeningsmodule]

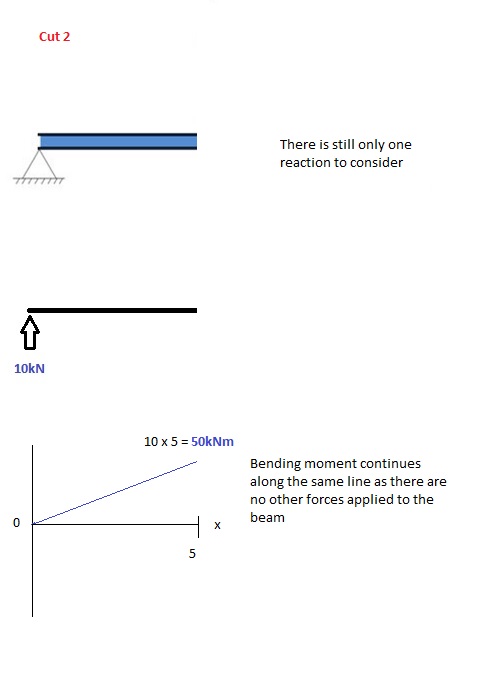
Snede 2

Deze snede wordt gemaakt net voor de tweede kracht langs de balk. Aangezien er geen andere belastingen worden toegepast tussen de eerste en tweede snede, de buigmomentvergelijking zal hetzelfde blijven. Dit betekent dat we het maximale buigmoment (in dit geval in het midden, of x = 5) kunnen berekenen door simpelweg x=5 in de bovenstaande vergelijking te vervangen:

Snede 3

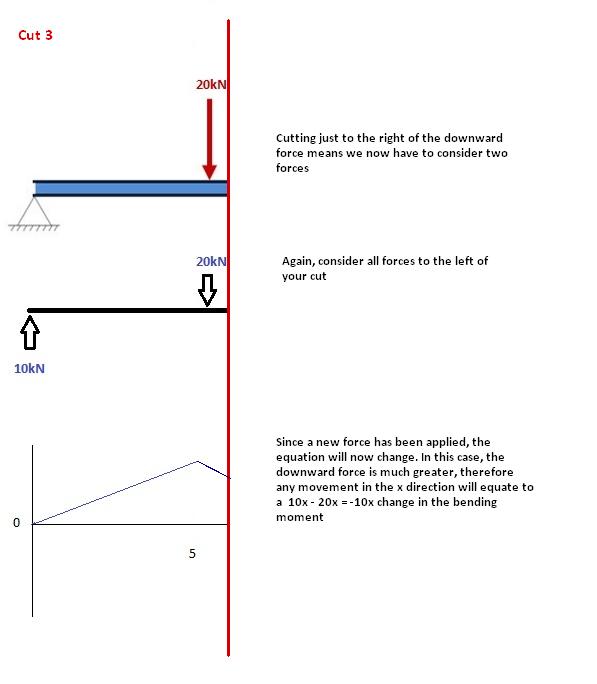
Deze snede wordt gemaakt net na de tweede kracht langs de balk. Nu hebben we TWEE krachten die links van onze snede werken: een reactie van 10 kN en een neerwaartse kracht van -20 kN. Dus nu moeten we beide krachten in overweging nemen terwijl we verder langs onze balk gaan. Voor elke meter die we langs de balk bewegen, wordt er een +10 kNm moment toegevoegd door de eerste kracht en -20 kNm door de tweede.

Dus na het punt x=5, wordt onze buigmomentvergelijking: M(X) = 50 +10(x-5) – 20(x-5) M(X) = 50 -10(x-5) voor 5 ≤ x ≤ 10 OPMERKING: De reden waarom we schrijven (x-5) is omdat we alleen de afstand vanaf het punt x=5 willen weten. Alles vóór dit punt gebruikt een eerdere vergelijking.[Bron: SkyCiv Beam Handberekeningsmodule]

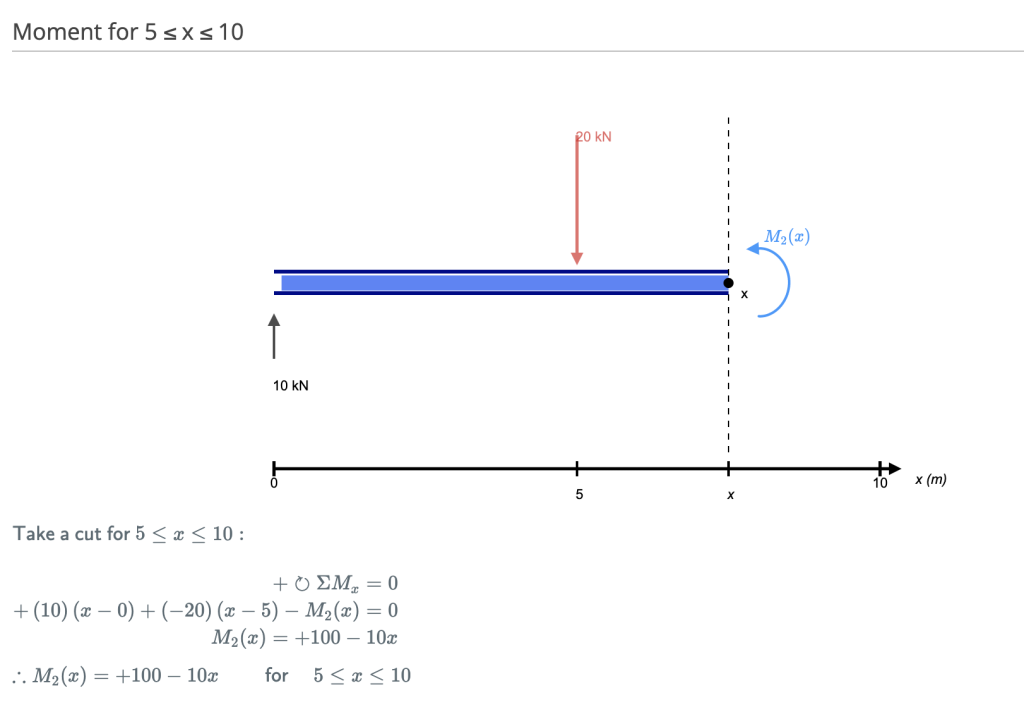
Snede 4

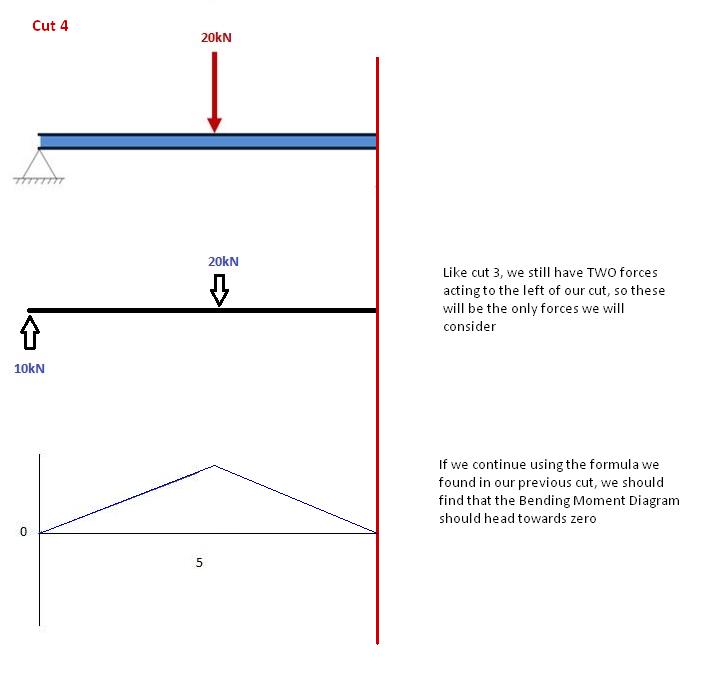
Opnieuw, we gaan weer verder naar rechts van onze balk en maken een snede net voor onze volgende kracht. In dit geval, zal onze volgende snede plaatsvinden net voor de reactie van de rechter steun. Aangezien er geen andere krachten zijn tussen de steun en onze vorige snede, blijft de vergelijking hetzelfde: M(X) = 50 -10(x-5) voor 5 ≤ x≤ 10 En laten we x=10 in deze vergelijking vervangen om het buigmoment aan het einde van de balk te vinden: M(X) = 50 – 10(10-5) = 0kNm Dit is volkomen logisch. Aangezien onze balk statisch is (en geen rotatie) is het logisch dat onze balk op dit punt geen momenten heeft als we al onze krachten beschouwen. Het voldoet ook aan een van onze beginvoorwaarden, namelijk dat de som van de momenten bij de steun gelijk is aan nul. OPMERKING: Als je berekeningen leiden tot een ander getal dan 0, heb je een fout gemaakt!

Het uiteindelijke resultaat, zoals weergegeven in SkyCiv Beam:

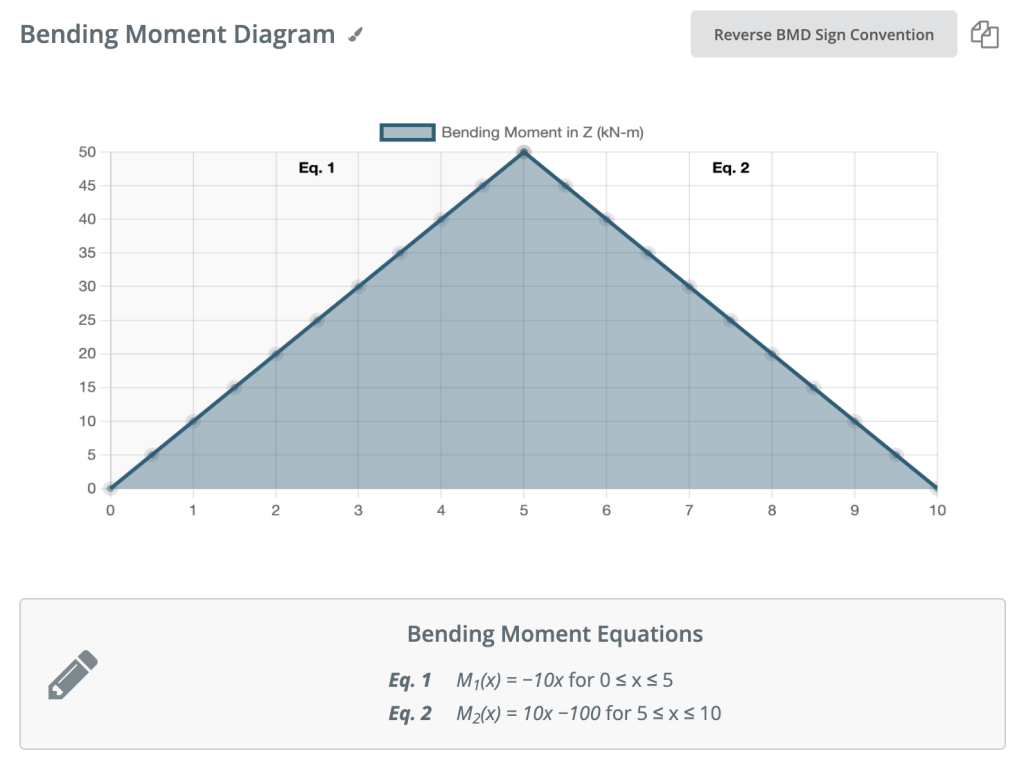
Tekenconventie voor Buigmomentdiagrammen

We hebben hierboven besproken hoe je buigmomenten kunt vinden. Buigmomentdiagrammen kunnen wat verwarrend zijn als het gaat om tekenconventies. e kunt hetzelfde diagram in tegengestelde richtingen getekend zien, afhankelijk van de bron. De tekenconventie die door SkyCiv wordt gebruikt, wordt hieronder weergegeven.

Positief Buigmoment:

Als het buigmoment positief is, wordt de bovenste vezel van de balk samengedrukt.

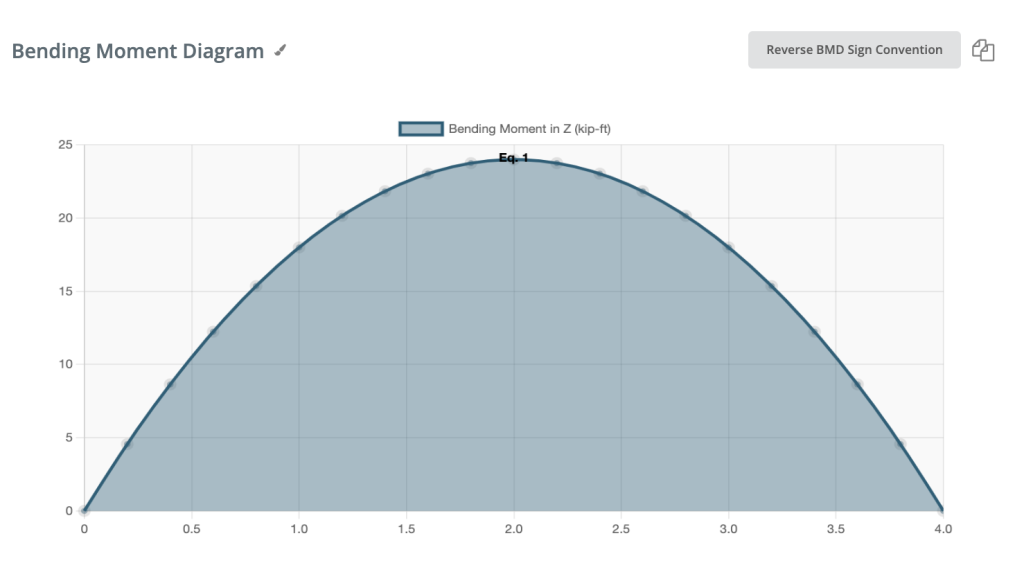
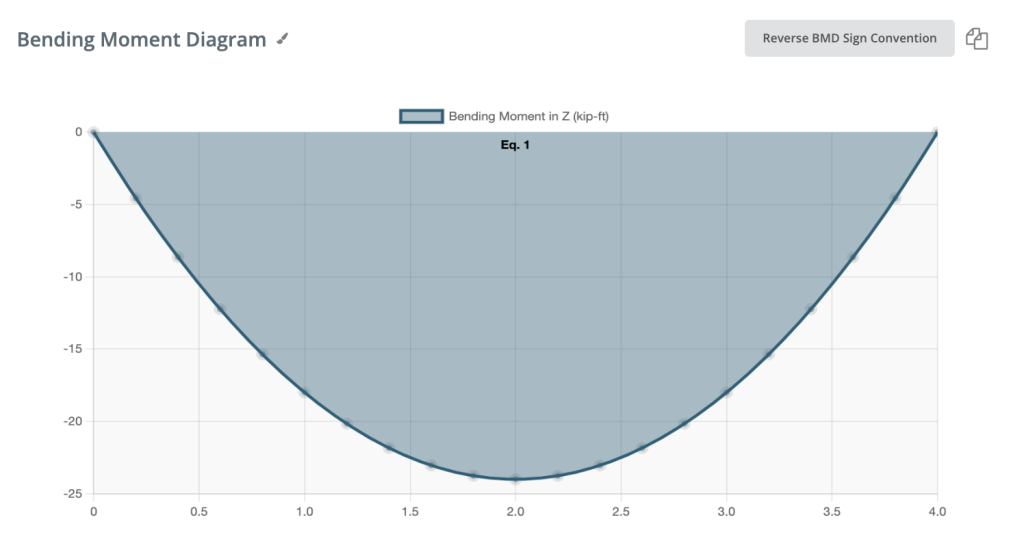
Negatief buigmoment:

Als het buigmoment negatief is, wordt de onderste vezel van de balk samengedrukt.

BONUS: Hoe buigmoment berekenen

Onder de betaalde versie van SkyCiv Beam de calculator je de volledige handberekeningen en de stappen die zijn genomen om je buigmomentdiagrammen handmatig te berekenen. Modelleer simpelweg je balk met de calculator, en klik op oplossen. Het toont je de stapsgewijze berekeningen van hoe je een buigmomentdiagram kunt tekenen (inclusief snedes):