Centroid Berekening: Een eenvoudige handleiding voor het berekenen van het zwaartepunt
Het zwaartepunt of massamiddelpunt van liggersecties is nuttig voor liggeranalyse wanneer het traagheidsmoment vereist is voor berekeningen zoals afschuiving/buigspanning en doorbuiging. Dit artikel leidt u door een eenvoudig proces voor het berekenen van het zwaartepunt en laat u kennismaken met SkyCiv Free Centroid Calculator.
Hoe het middelpunt te vinden
Allereerst, je moet weten hoe je het zwaartepunt kunt vinden. Balksecties bestaan meestal uit een of meer vormen. Dus om het zwaartepunt van een hele straalsectie te vinden, het moet eerst worden opgesplitst in geschikte segmenten. Na dit, het gebied en het zwaartepunt van elk afzonderlijk segment moeten worden overwogen om het zwaartepunt van de hele sectie te vinden.
Hoe het middelpunt te berekenen (Zwaartepunt vergelijking):
Overweeg het onderstaande I-balkgedeelte. Om het verticale zwaartepunt te berekenen (in de y-richting) het kan worden opgesplitst 3 segmenten zoals afgebeeld:
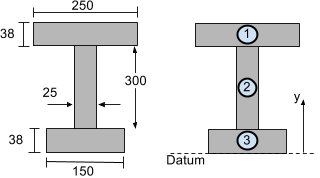
Nu hoeven we alleen de zwaartepuntvergelijking te gebruiken voor het berekenen van de verticaal (y) waartepunt van een meersegmentvorm te berekenen:

We nemen de datum of referentielijn vanaf de onderkant van de balksectie. Laten we nu A zoekenik en yik voor elk segment van de I-balk sectie hierboven weergegeven, zodat de verticale of y zwaartepunt kan worden gevonden.
[wiskunde]
\tekst{Segment 1:}\\
\beginnen{uitlijnen}
{A}_{1} &= 250 keer38 = 9500 {\tekst{ mm}}^{2}\\
{y}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \tekst{ mm}\\\\
\einde{uitlijnen}
[wiskunde]
[wiskunde]
\tekst{Segment 2:}\\
\beginnen{uitlijnen}
{A}_{2} &= 300 keer25 = 7500 {\tekst{ mm}}^{2}\\
{y}_{2} &= 38 + \tfrac{300}{2} = 188 \tekst{ mm}\\\\
\einde{uitlijnen}
[wiskunde]
[wiskunde]
\tekst{Segment 3:}\\
\beginnen{uitlijnen}
{A}_{3} &= 38 keer150 = 5700 {\tekst{ mm}}^{2}\\
{y}_{3} &= tfrac{38}{2} = 19 tekst{ mm}\\\\
\einde{uitlijnen}
[wiskunde]

In het geval dat de doorsnede bestaat uit twee materialen of een composietmateriaal, dan zal een van de materialen moeten worden vermenigvuldigd met de modulaire verhouding, zodat de volledige doorsnede van de vergelijking uniform wordt.
[wiskunde]
n = frac{E_{1}}{E_{2}}
[wiskunde]
Typisch, E1 is de elasticiteitsmodulus van het niet-heersende materiaal, en E2 is de elasticiteitsmodulus van het overheersende materiaal, hoewel de volgorde van voorkeur de oplossing van het zwaartepunt niet zal beïnvloeden. Aanpassing voor het tweede materiaal, de zwaartepuntvergelijking wordt het volgende:.
[wiskunde]
\bar{y}= frac{\som{A}_{ik}{y}_{ik}+\som {n}{A}_{ik}{y}_{ik}}{\som{A}_{ik}+\som {n}{A}_{ik}}
[wiskunde]
Bereken het zwaartepunt van de straal met SkyCiv
Het berekenen van het zwaartepunt van de straal is belangrijk, maar het handmatig berekenen ervan kan tijdrovend zijn. SkyCiv biedt een Gratis centroid rekenmachine dat dit proces voor u automatiseert, helpt u de verticaal te vinden (y) en horizontaal (X) zwaartepunten van straalsecties eenvoudig en nauwkeurig!
Deze tool is een gratis versie van SkyCiv Sectiebouwer, een uitgebreide online software voor sectieanalyse om geometrische analyses uit te voeren, buigen, eigenschappen van afschuif- en torsieprofielen, evenals FEA- en gewapend betonontwerp. Met dit hulpmiddel, u kunt aangepaste secties maken met behulp van vooraf gedefinieerde sjablonen of uw eigen vormen met punten definiëren, lijnen, of DXF-import vanuit CAD.
Om alle functionaliteit te verkennen SkyCiv Sectiebouwer en ervaar het gemak van het modelleren en analyseren van uw sectie, meld u vandaag nog GRATIS aan!
Bezoek de volgende stap: Berekenen van het Statisch/Eerste Oppervlakte Moment.

